大跨徑鋼橋面瀝青鋪裝層有限元分析

王剛，林樹鋒，陳翠婷，陸雅婷，鄒婉婷，陶子豪，王宏暢

0 引言

橋面鋪裝層作為大跨徑鋼橋的重要組成部分，疲勞開裂問題是橋面鋪裝層最主要的破壞形式之一[1-3]。德國最早開始對鋪裝層材料的選擇和設計及其相關性能進行了試驗分析，隨后美國學者研究了鋼橋面鋪裝層的疲勞性能，建立了疲勞斷裂力學模型并探索了在連續反復荷載的作用下鋼橋面鋪裝層疲勞裂紋的發展規律[4]。Kainuma通過總結日本鋼橋疲勞現狀，分析研究單日過橋重載車輛數得出預防鋼橋開裂的措施[5]。國內對正交異性鋼板的研究相對較晚，其研究基本上都是對鋼橋面鋪裝層疲勞開裂的過程探索以及如何對其進行有效的預防。如單海燕[6]等通過實地病害調查，認為由于鋪裝層的開裂而進一步導致瀝青鋪裝的龜裂、車轍等次生病害的發生，并提出了相應的預防措施。鄧學鈞[7]等運用有限條法計算得出了不同荷位對鋪裝層表面縱向與橫向拉應力的影響，鋪裝層表面橫向最大拉應力遠大于縱向拉應力的結論。邵臘庚[8]等通過足尺試驗對比分析研究后得出了導致瀝青鋪裝層破壞的原因。張起森[9]等根據廈門海滄大橋建立了足尺模型進行了疲勞試驗研究不同的結構和材料對其疲勞性能的影響等。但是國內外部分大跨徑鋼橋在建成通車后都會相繼出現瀝青鋪裝層與鋼橋面板的疲勞開裂，而目前將兩者結合起來考慮研究鋪裝層受力狀況及疲勞裂縫擴展的研究比較少[10-13]，因此研究正交異性板在開裂狀態與完好狀態下鋪裝層的受力情況很有必要。對橋面鋪裝層裂縫進行計算分析，關鍵是計算鋪裝層的應力或應力強度因子，一般利用解析法很難直接求出應力強度因子，需要運用有限元方法計算出應力強度因子。故本文應用有限元軟件ABAQUS，分別建立4種不同的三維有限元模型，分析計算橋面不同工作狀態下橋面鋪裝層的應力與應力強度因子的大小。

1 鋼橋面瀝青鋪裝層基本計算模型

1.1 幾何模型

本文依托虎門大橋的基本參數，建立鋼橋面鋪裝的有限元基準模型[12]。有限元模型橫向取八個U型加勁肋，縱向取三跨，計算模型的基本尺寸見表1。材料參數見表2，橫隔板與加勁肋連接形式如圖1所示[13-15]。

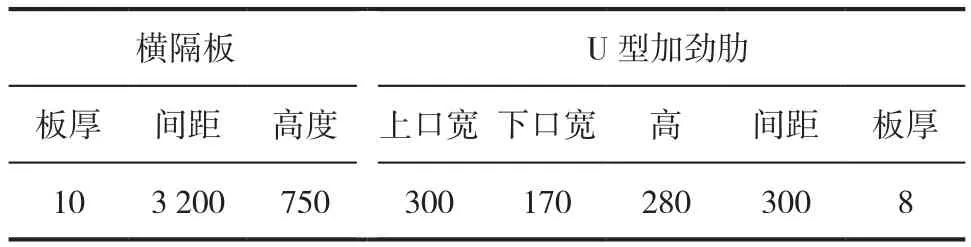
表1 有限元模型尺寸 mmTab.1 FEM model size

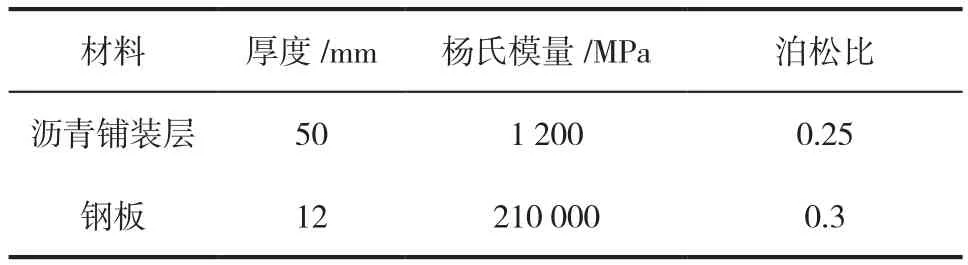
表2 材料參數Tab.2 Material parameters

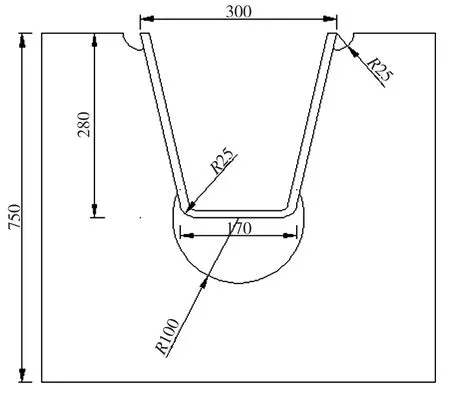
圖1 橫隔板與縱向加勁肋的型式（mm）Fig.1 Type of transverse bulkhead and longitudinal stiffening rib（Unit: mm）

1.2 基本假定

鋼橋面鋪裝有限元模型的假定如下[16-17]：

（1）忽略瀝青混凝土的粘彈性特性，假定瀝青混凝土為均勻、連續、各向同性的材料，采用線彈性理論分析鋪裝層的受力。

（2）假定瀝青鋪裝層與鋼橋面板之間為完全連續的。

（3）不考慮瀝青鋪裝層與橋面系的自重。

1.3 邊界條件及車輛荷載的簡化

鋼橋面板與瀝青鋪裝層不允許有橫向位移，但可以有豎向位移，橫隔板頂部完全約束。車輛荷載作用為0.2 m×0.6 m的矩形單輪均布荷載，荷載大小為0.7 MPa。荷載橫向位置分3種荷位加載[19-21]，分別為單輪荷載中心作用在：①在兩相鄰加勁肋中心的鋪裝層表面處；②在加勁肋側肋的鋪裝層表面處；③在加勁肋開口中心的鋪裝層表面處。

荷載縱向加載位置分兩種荷位：①兩橫隔板中心處；②橫隔板頂部。

1.4 單元類型的選擇及網格尺寸

鋼橋面板、U型加勁肋及橫隔板均采用ABAQUS中的殼單元S4R進行模擬。瀝青鋪裝層則采用實體單元C3D8來進行模擬。模型的全局尺寸采用50 mm，在加載位置進行局部網格加密，尺寸為20 mm。

2 鋼橋面板與鋪裝層不同工作狀態下的有限元分析

2.1 鋼橋面板與鋪裝層完好狀態下的受力分析

當鋼橋面板與鋪裝層都處于完好狀態下時，一般為鋼橋初建成通車，這是最基本的形態。但是在最不利位置的外荷載反復作用之下，瀝青鋪裝層很有可能在最大應力處出現疲勞裂縫。分析此狀態下鋪裝層的受力，可以得出其最大拉應力及應變出現的位置，從而可以分析得到鋪裝層最有可能產生疲勞裂縫的位置。

2.1.1 縱向加載位于兩橫隔板中心處時

對于荷載橫向作用的3種荷位，瀝青鋪裝層受力計算見表3。

從表3中的數據可以看出，鋪裝層在不同荷載位置的作用下，受力狀況是不同。但是很明顯當荷載作用在位置①、②、③時，鋪裝層受到的橫向應力與應變均大于縱橋向，并且前者是后者的兩倍之多，這表明橫橋向的應力與應變是控制鋪裝層應力的主要因素。這也就解釋了鋼橋面鋪裝層的總是出現縱向裂縫的原因。從表3中可以看出，3種荷位下的鋪裝層最大橫向拉應力均與最大主拉應力σ1的大小相差無幾，但是由于最大主拉應力不能直接測量得出且方向也不易確定，所以可以將橫向最大拉應力作為鋪裝層應力狀態的一個重要指標。

表3 單輪均布荷載作用下鋪裝層的受力Tab.3 Single wheel loads paving layer stress

可以從表3看到，荷位①作用下的橫向最大拉應力比其他兩種荷位略小，荷位③作用下的鋪裝層橫向最大拉應力最大，可以認為荷位③為最不利荷載位置。鋪裝層內σxmax與σzmax均出現在鋪裝層的上表面。對于σxmax，其縱向位置出現在荷載作用附近，即跨中位置。而σzmax的縱向位置則出現在橫隔板頂部。

2.1.2 縱向加載位于橫隔板頂部時

當荷載縱向位于橫隔板頂部時，對于3種荷位，鋪裝層受力計算見表4。

從表4可以看出，荷位②最大應力與應變值最大，荷位③次之，荷位①最小。當荷載作用于橫隔板頂部時，無論橫向作用位置如何，鋪裝層最大應力與應變值均小于荷載作用于跨中的情況。以荷位②作為此時的最不利荷載位置，相比荷載作用于跨中情況，σxmax減小了270%，σzmax減小了135%，εxmax減小了206%，εzmax略有增大，增大了18%，可見橫隔板增大了局部區域的剛度，減小了上方鋪裝層的受力。當荷載作用于橫隔板頂部時，雖然鋪裝層應力應變均有減小，但σxmax仍然遠大于σzmax，說明此時橫向拉應力仍是控制鋪裝層開裂破壞的主要因素。

表4 荷載位于橫隔板頂部時鋪裝層的受力Tab.4 Located load force when the cross at the top of the separator pavement

2.2 鋼橋面板出現裂縫且鋪裝層完好狀態下的應力分析

為了研究正交異性鋼橋面板出現疲勞裂縫后對鋪裝層應力分布的不利影響，建立鋼橋面開裂且鋪裝層完好狀態下的有限元模型。大跨徑鋼橋正交異性鋼板疲勞裂縫主要分布在縱肋與橋面板焊接處、縱肋與橫隔板的焊接處及三者共同相接處，即第1類裂縫與第2類裂縫，通常裂縫的長度在20～150 mm。故取鋼橋面板裂縫長70 mm，第1類裂縫縱向位置分跨中和橫隔板頂部兩種位置設置，橫向位置為縱向加勁肋與橋面板焊接處；第2類裂縫為橫隔板與加勁肋焊接處，設置在邊跨的橫隔板上，荷載作用位置為荷位③。

模型分析中鋼橋面板采用殼單元進行模擬，直接利用ABAQUS中的Crack設置70 mm長的鋼橋面裂縫。經計算鋪裝層各項應力與應變值見表5。

從表5可以看出，當鋼橋面板出現第1類裂縫并且位于跨中位置時，鋪裝層表面的各項受力比其他兩種情況略大，第2類鋼橋面裂縫時鋪裝層的受力情況與第1類裂縫位于橫隔板頂部時相差不大。

表5 鋼板出現裂縫時鋪裝層拉應力與拉應變Tab.5 Tensile stress and tensile strain of steel plate in the course of crack

取第1類裂縫位于跨中時的鋪裝層狀態為研究對象，與鋼橋面和鋪裝層都完好狀態下的鋪裝層受力（表3）相比，荷載大小位置都相同，鋪裝層受到的σxmax增大了45%，σzmax增大了66%，εxmax增大了37%，εzmax增大了124%。計算結果表明當跨中位置的鋼橋面板與加勁肋焊接處出現了裂縫后，在行車荷載的作用下，鋪裝層的各項受力均有較大幅度的增加，這將加速鋪裝層由于縱向裂縫的產生引起的疲勞破壞，同時縱向拉應力與應變增幅較大，說明有可能會導致橫向裂縫等次生裂縫的進一步發展。所以，當鋼橋面出現裂縫后，應該及時采取有效措施來進一步阻止裂縫的繼續擴展。

2.3 鋼橋面板完好且鋪裝層出現裂縫時的有限元分析

從前面的分析結果可以看出，鋪裝層表面的橫向拉應力與拉應變的最大位置出現在縱向加勁肋頂部，是最容易發生開裂的位置。建立鋼橋面完好且鋪裝層開裂狀態下的斷裂有限元模型，與鋪裝層完好狀態下的受力進行比較分析，計算出裂縫的應力強度因子，由此可以分析裂縫的擴展趨勢。

2.3.1 鋪裝層出現縱向裂縫時的有限元分析

分析模型與前述基本模型保持一致，其他基本條件不變，荷載位置為荷位③。根據前述的分析，鋪裝層內的最大應力出現在鋪裝層表面，且荷載位置出現在跨中時，鋪裝層表面σxmax最大。因此設在加勁肋側肋頂部的鋪裝層表面有一條縱向裂縫（即位于鋪裝層σxmax處），深度為25 mm，長度為120 mm。裂縫前沿布置20節點空間等參奇異單元。

在鋪裝層出現裂縫后，裂縫區域會出現應力集中效應，會使表面計算應力偏大，為了避免這種情況，結果分析時，避開應力集中區域，選取縱向距離 4 500 mm（縱向距離4 800 mm為跨中位置）的橫向各點計算鋪裝層最大應力與應變。鋼橋面瀝青鋪裝層在完好的工作情況下與出現縱向裂縫后，鋪裝層各項受力計算結果見表6。

表6 鋪裝層完好與縱向開裂狀態下受力比較Tab.6 Comparison of the stress of the pavement layer under the condition of intact and longitudinal crack

由表6可以看出，與鋪裝層完好狀態下相比，當鋪裝層表面出現縱向開裂后，各項受力均有明顯的增大。其中，σxmax比鋪裝層完好情況增大了130%，σzmax增大了 609%，εxmax增大了 119%，εxmax增大了989%。縱向拉應力與應變增幅非常大，這說明當鋪裝層出現縱向開裂后，裂縫附近的鋪裝層將失去傳遞承載行車荷載的作用，有效鋪裝層寬度變小，從而導致鋪裝層應力突增。因此，在橋梁的日常養護中，當發現鋪裝層出現裂縫后，應及時采取有效措施對裂縫進行修補，阻止裂縫的進一步擴展。

現取鋪裝層跨中位置的橫向各點的橫向拉應力、縱向拉應力，繪制出變化趨勢曲線，如圖2和圖3所示，將鋪裝層完好狀態下與縱向開裂狀態下鋪裝層的受力變化進行比較。

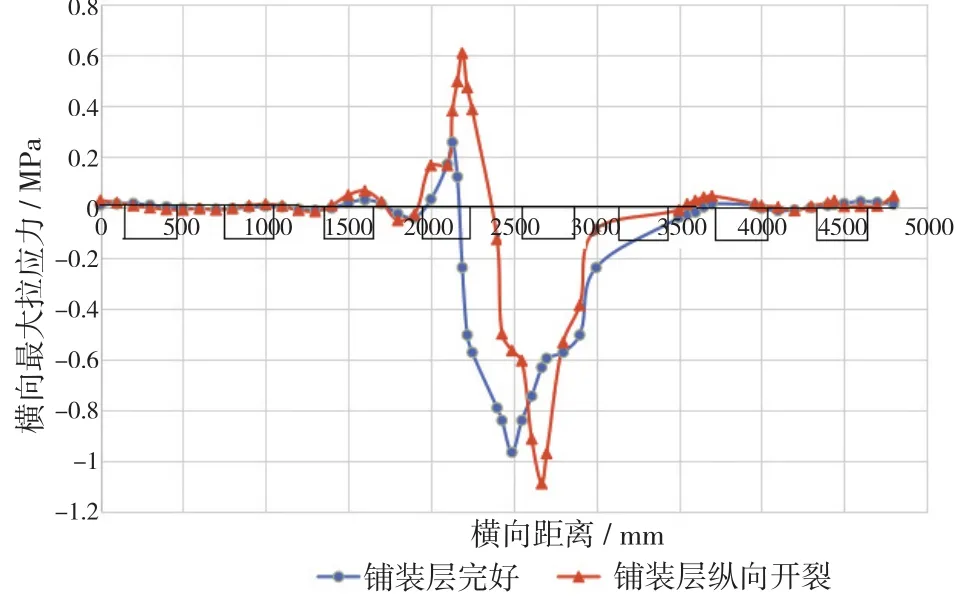
圖2 鋪裝層完好與縱向開裂時的橫向拉應力比較Fig.2 Comparison of the transverse tensile stress of the pavement layer when the pavement is in good condition and in the longitudinal direction

圖3 鋪裝層完好與縱向開裂時的縱向拉應力比較Fig.3 Comparison of longitudinal tensile stress between pavement layer and longitudinal crack

從圖2中可以看出，兩種不同鋪裝層破壞情況下，鋪裝層拉應力的變化趨勢大致一致，鋪裝層所受的σx分布形狀相似，都在荷載作用的附近位置出現峰值與谷值。在荷載作用區域的邊緣處，鋪裝層受到的σx出現峰值；在荷載作用的中心區域，σz出現谷值，而在鋪裝層的兩端拉應力很小幾乎為0。但是，與鋪裝層完好狀態下相比，在鋪裝層出現縱向裂縫后，鋪裝層的縱向拉應力在荷載作用區域附近迅速增大，達到峰值，然后又迅速達到最小值，這是由于加勁肋的作用使頂部的鋪裝層形成高應力區域。

從圖3可以看出，與鋪裝層完好狀態下相比，鋪裝層縱向開裂后，兩者變化趨勢并不相同，σz大幅度增加，在加勁肋側肋附近出現交替正負變化，σzmax僅略小于σxmax，這說明此時的鋪裝層很有可能會出現橫向裂縫。

鋪裝層斷裂的有限元分析還有一項非常重要的任務就是應力強度因子的計算。由于在外荷載的作用下，本研究所建立的三維裂縫沿著裂縫前沿不同截面上的應力強度因子的大小是不同的，所以把整條120 mm裂縫從縱向長度起始處按照0、30、60、90、120 mm，分成5個截面來計算裂縫尖端的應力強度因子值，分別為i、ii、iii、iv、v。

本文所建立的鋪裝層裂縫為三維裂縫，裂縫擴展的形式是Ⅰ、Ⅱ、Ⅲ三種開裂形式共同作用的結果，所以每個截面的裂縫尖端都必須計算出KⅠ、KⅡ、KⅢ三種因子強度因子的值，并且采用三種應力強度的因子組合形式，即等效應力強度因子來反映裂縫受到三種開裂方式綜合作用下的擴展形式。從工程安全角度考慮，本文采用公式（1）來表示等效應力強度因子Ke。

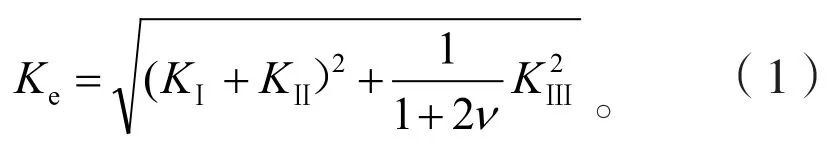
式中：v為泊松比。

表7為鋪裝層出現縱向裂縫時各基本開裂模式的應力強度因子以及等效應力強度因子的計算值，表7中應力強度因子的單位為MPa·mm1/2。

表7 縱向裂縫尖端應力強度因子 MPa·mm1/2Tab.7 Longitudinal crack tip stress intensity factor

裂縫尖端的應力強度因子主要表征了裂紋沿著厚度方向擴展的趨勢。由上表可以看出，無論哪種計算截面，裂縫尖端的KⅠ值遠大于，KⅡ和KⅢ，說明當鋪裝層出現縱向裂縫后，在受到車輪豎向荷載的作用時，鋪裝層裂縫尖端處很有可能沿著厚度方向發生張開型失穩擴展。

2.3.2 鋪裝層出現橫向裂縫時的有限元分析

無論哪種加載方式，鋪裝層表面都在橫隔板處U型加勁肋的頂部出現最大縱向拉應力與應變。分析模型與前述基本模型保持一致，其他基本條件不變，荷載位置為荷位③。因此設在橫隔板與鋼橋面板焊接處的鋪裝層表面有一條橫向裂縫（即位于鋪裝層縱向最大拉應力處），深度為25 mm，長度為120 mm。為避免應力集中現象，利用同樣的方法來計算鋪裝層表面的最大應力與應變值。鋼橋面瀝青鋪裝層在完好的工作情況下與出現橫向開裂后，鋪裝層各項受力計算結果的比較見表8。

表8 鋪裝層完好狀態下與橫向開裂狀態下受力比較Tab.8 Comparison of stress between pavement layers under condition of complete state and transverse cracking

由表8計算結果中可以看出，鋪裝層橫向最大拉應力仍大于縱向最大拉應力，橫向拉應力仍是控制鋪裝層開裂的主要因素。其中σxmax增大了63.71%，σzmax增大了64%，εxmax增大了61.69%，εzmax增大了126.3%，可見鋪裝層各項應力應變值均有增加，且幅度基本相同，但是不如出現縱向裂縫時鋪裝層的受力變化幅度大。

以同樣的方法選取裂縫長度方向五個不同截面i、ii、iii、iv、v來計算裂縫尖端的應力強度因子以及等效應力強度因子的值。計算結果見表9。

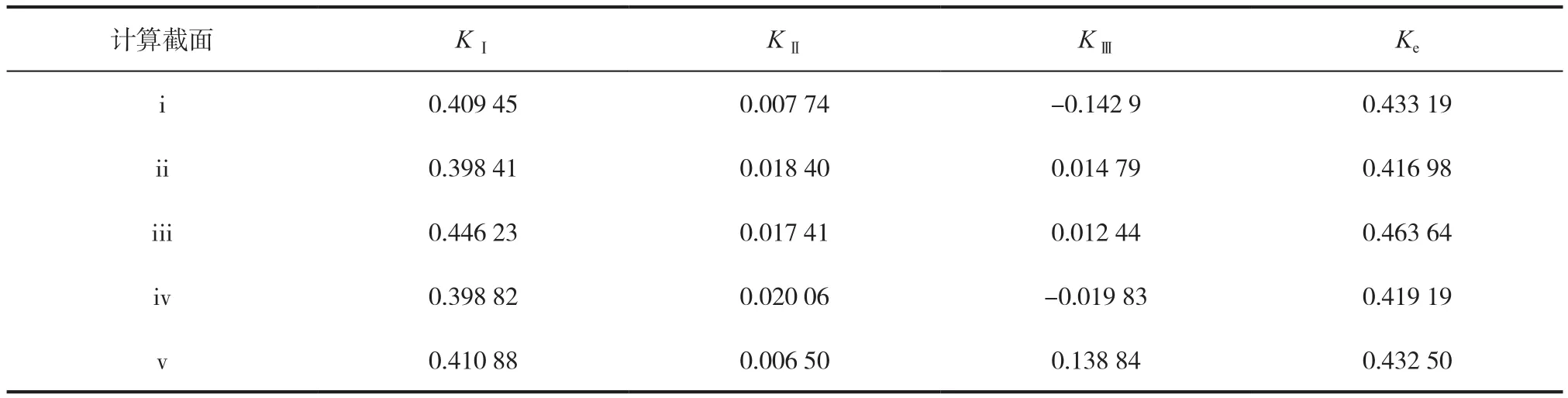
表9 不同截面橫向裂縫尖端應力強度因子 MPa·mm1/2Tab.9 Transverse crack tip stress intensity factor of different cross section

從表9計算結果可以看出，KⅠ仍遠遠大于KⅡ與KⅢ的值，等效應力強度因子Ke的大小主要還是由KⅠ決定。這說明鋪裝層出現橫向裂縫后，在外荷載的作用下，鋪裝層裂縫尖端處很有可能發生張開型失穩擴展。

2.4 鋼橋面板帶裂縫工作且鋪裝層出現裂縫時的有限元分析

當正交異性鋼橋面板出現第一類裂縫且位于跨中位置時，鋪裝層受力變化較為明顯，所以這里取一條長為70 mm位于加勁肋與橋面板焊接處的縱向鋼橋面板裂縫，縱向位置為跨中。加載方式為荷位③，其他條件不變，建立鋼橋面板帶裂縫工作且鋪裝層開裂時的有限元模型。

2.4.1 帶縱向裂縫的鋪裝層有限元分析

設加勁肋側肋頂部的鋪裝層表面有一條縱向裂縫（即位于鋪裝層橫向最大拉應力處），深度為25 mm，長度為120 mm。裂縫前沿仍布置20節點空間等參奇異單元，網格劃分與前述方式相同。

經計算，鋪裝層內各項受力大小與前面3種不同狀態下的鋪裝層受力比較見表10，為敘述簡便，將4種不同的狀態依次編號為1、2、3、4。

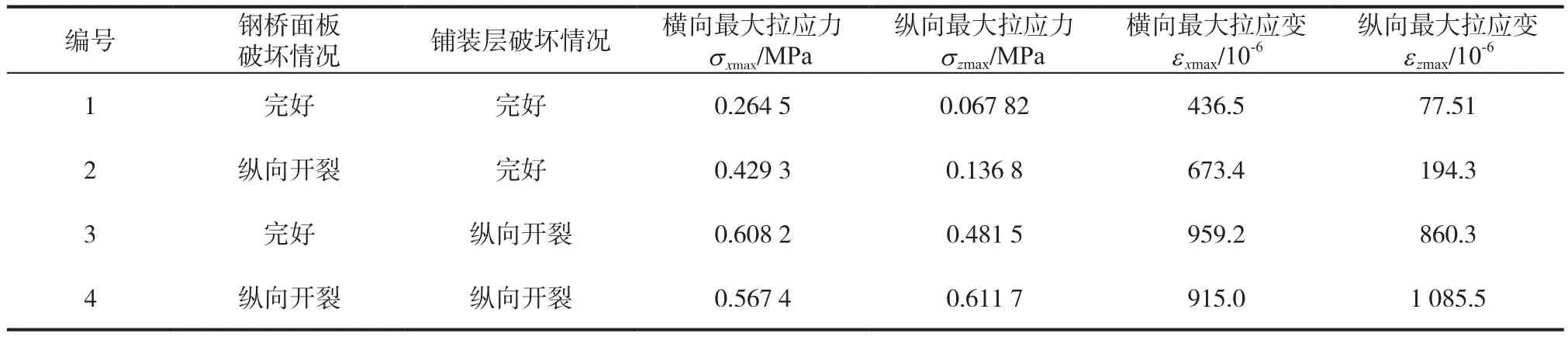
表10 鋼橋面板與鋪裝層處于不同破壞狀態下的受力Tab.10 The stress of steel bridge deck and pavement layer under different damage conditions

從表10中可以看出，σmax與εmax的總體變化趨勢相同。當鋼橋面板和鋪裝層中的一者出現縱向裂縫時，鋪裝層表面σmax與εmax都表現出明顯的增大趨勢；但是當兩者同時出現裂縫時，σxmax與εxmax卻略有減小，而此時鋪裝層σzmax與εzmax卻仍在增加，甚至已經超過了σxmax與εxmax的值，說明此時的狀態對鋪裝層橫向有應力松弛效應，使得縱向裂縫附近鋪裝層的應力、應變值減小，而縱向拉應力的繼續增大會進一步導致橫向裂縫的發展。

當鋼橋面板出現縱向裂縫，鋪裝層出現縱向裂縫時，以同樣的方法選取5個截面，鋪裝層裂縫前沿5個截面的應力強度因子的計算值見表11。

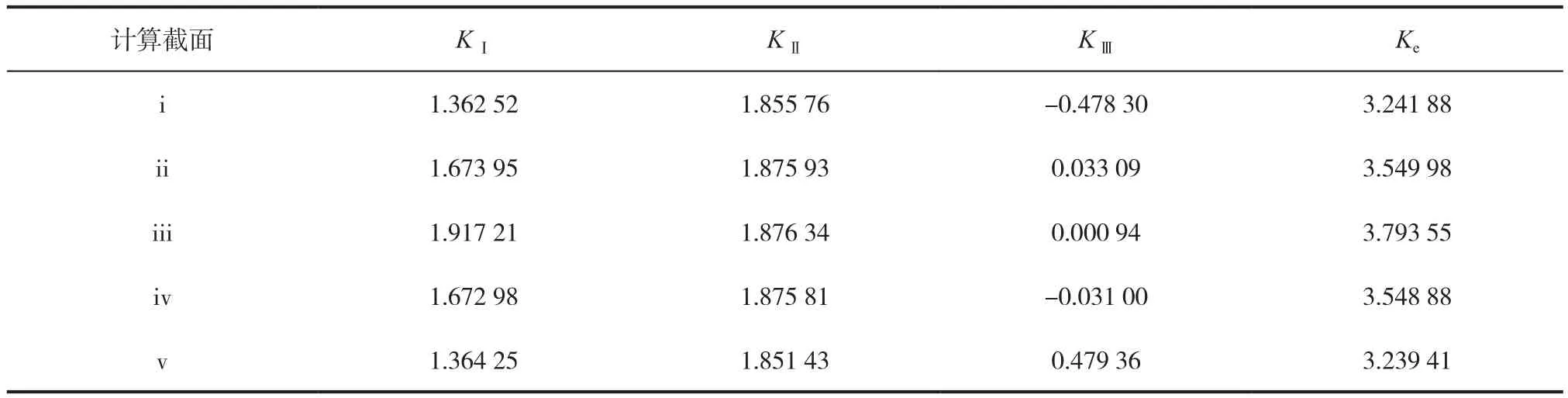
表11 鋪裝層裂縫前沿不同截面應力強度因子 MPa·mm1/2Tab.11 Stress intensity factor of different cross section in the front of pavement crack

選擇5個截面的最大值代表整個裂縫尖端的應力強度因子的值，與前面的計算應力強度因子的值對比可知，KⅠ與Ke的值略有減小而剪切型應力強度因子顯著增大，說明此時剪切作用對裂縫的擴展有一定的影響。應力強度因子的比較見表12。

表12 鋼橋面板與鋪裝層不同開裂狀態下應力強度因子的比較 MPa·mm1/2Tab.12 Comparison of stress intensity factors of steel bridge deck and pavement under different cracking conditions

從表12中比較可知，在鋪裝層縱向開裂的情況下，與鋼橋面完好狀態下相比較，鋼橋面出現縱向開裂后，鋪裝層表面裂縫的KⅠ減小了30%，但是KⅡ卻迅速增大，增大了266%，KⅢ基本不變，等效應力強度因子Ke略有增大。這表明，鋼橋面板的開裂使得鋪裝層表面裂縫的破壞類型變為張拉型與滑移型的組合破壞，由KⅠ與KⅡ共同決定。

2.4.2 帶橫向裂縫的鋪裝層有限元分析

設在橫隔板與鋼橋面板焊接處的頂部鋪裝層表面有一條橫向裂縫（即位于鋪裝層縱向最大拉應力處）深度為25 mm，長度為120 mm。

鋪裝層內各項受力計算結果見表13。

表13 鋪裝層在不同破壞狀況下的受力狀況比較Tab.13 Comparison of stress state of pavement layer under different damage conditions

從表13可以看出，鋪裝層σxmax相比略有增大，說明當鋪裝層出現橫向裂縫時，鋼板的縱向開裂有可能會導致鋪裝層新的縱向裂縫的產生。

當鋼橋面板出現縱向裂縫，鋪裝層出現橫向裂縫時，鋪裝層裂縫前沿5個截面的應力強度因子的計算值見表14。

表14 鋪裝層出現橫向裂縫應力強度因子的計算 MPa·mm1/2Tab.14 Calculation of stress intensity factor of transverse crack in pavement

選擇5個截面的最大值代表整個裂縫尖端的應力強度因子的值，與鋼橋面完好狀態下的裂縫尖端應力因子的值相比較見表15。

表15 鋼橋面板與鋪裝層不同開裂狀態下應力強度因子的比較 MPa·mm1/2Tab.15 Comparison of stress intensity factors of steel bridge deck and pavement under different cracking conditions

從表15的比較可以看出，在橋面鋪裝層橫向開裂的情況下，鋼橋面板出現縱向開裂時，鋪裝層裂縫KⅠ增大了23%，KⅡ、KⅢ變化較小，等效應力強度因子Ke增大了24%。這說明，鋼橋面板的縱向開裂，會加劇鋪裝層橫向裂縫的張開型破壞，降低鋪裝層的疲勞壽命。

3 結論

（1）建立鋼橋面板與鋪裝層都完好狀態下的有限元模型，計算表明最不利荷位是縱向位于兩橫隔板中心處加載，橫向單輪荷載中心作用在加勁肋開口中心的鋪裝層表面處。鋪裝層受到的橫向應力與應變均大于縱橋向，而且最大橫向拉應力與應變均出現在鋪裝層的上表面，橫向應力應變約是縱向應力應變的4倍左右。

（2）建立鋼橋面板開裂而鋪裝層完好狀態的有限元模型，經計算對比后發現，當鋼橋面板跨中位置出現了裂縫后，在行車荷載的作用下，鋪裝層的各項受力均有較大幅度的增加，其中σxmax增大了45%，σzmax增大了66%，εxmax增大了37%，εzmax增大了124%。這說明鋼橋面板的開裂會導致鋼橋面鋪裝層的進一步破壞。同時縱向拉應力與應變增幅較大，說明會導致鋪裝層產生橫向開裂。

（3）建立鋼橋面板完好且鋪裝層開裂的有限元模型，與鋼橋面板和鋪裝層都完好的狀況相比較，發現鋪裝層開裂后最大拉應力與拉應變增幅很大，其中，σxmax比鋪裝層完好情況增大了130%，σzmax增大了 609%，εxmax增大了 119%，εzmax增大了989%。表面裂縫的應力強度因子、KⅡ、KⅢ較小，此時表明裂縫主要呈張開型擴展。

鋼橋面板與鋪裝層均開裂的狀態下，與鋼橋面板完好且鋪裝層開裂的狀況下比較發現，鋪裝層σxmax與εxmax略有減小，但是σzmax與εzmax仍在增加且此時甚至大于超過前者，說明此時鋼橋面板的開裂使鋪裝層極易產生橫向裂縫。而KⅠ增大了23%、KⅡ增大了31%，KⅢ接近為0，表明此時裂縫的擴展主要是張開型和滑移型這兩種方式的共同作用。

［1］崔海軍.正交異性閉口加勁鋼橋面板力學及疲勞性能研究［D］.揚州 : 揚州大學, 2009.

［2］彭小波.動載下粘貼GFRP的環氧瀝青混凝土鋼橋面鋪裝受力分析［D］.重慶 : 重慶交通大學, 2017.

［3］吉林, 李洪濤.大跨徑鋼箱梁懸索橋環氧瀝青混合料鋪裝技術［J］.公路, 2005(11) : 74-76.

［4］Kornel K ,Laszlo D .Fracture mechanics based fatigue analysis of steel bridge decks by two-level cracked models［J］.Computers and Structures,2002;80:2321-2331.

［5］Kainuma S, Jeong Y S, Ahn J H, et al. Behavior and stress of orthotropic deck with bulb rib by surface corrosion［J］. Journal of Construction Steel Research, 2015, 113(10): 135-145.

［6］單海燕,馬海峰.防水混凝土橋面鋪裝層裂縫產生的原因及防治［J］.遼寧省交通高等專科學校學報,2004,6(2)：11-12.

［7］鄧學鈞,顧學宇,周世忠, 等.鋼橋面瀝青鋪裝層裂縫破壞趨勢研究［J］.公路交通科技,2005,22(6) :89-93.

［8］邵臘庚,李宇峙.正交異性鋼橋面瀝青鋪裝結構特性的研究［J］.公路交通科技,2005,22(6) :89-93.

［9］張起森,李宇峙,邵臘庚, 等.廈門海滄大橋橋面瀝青鋪裝層直道疲勞試驗研究［J］.中國公路學報,2001,13(1) :6-12.

［10］鐘科, 陳飛, 魏小皓, 等. 基于加速加載試驗的鋼橋面鋪裝性能研究［J］.公路交通科技, 2017, 34(11) : 50-56.

［11］王民, 周啟偉, 胡德勇, 等. 三種不同鋼橋面鋪裝材料的疲勞特性分析［J］.華南理工大學學報(自然科學版), 2016,41(3) : 40-42.

［12］張肖寧, 容洪流, 黃文柯, 等. 大型MA類鋼橋面鋪裝高溫性能加速加載試驗研究［J］.華南理工大學學報(自然科學版), 2014, 42(12) : 21-26.

［13］錢振東, 黃衛, 駱俊偉, 等.正交異性鋼橋面鋪裝層的力學特性分析［J］.交通運輸工程學報, 2002, 2(3) : 47-51.

［14］趙欣欣, 劉曉光, 張玉玲.正交異性橋面板設計參數和構造細節的疲勞研究進展［J］.鋼結構, 2010, 25(8)：1-7.

［15］李兆霞, 郭力, 徐玉兵, 橋梁焊接構件疲勞損傷測試與分析［J］.東南大學學報(自然科學版), 2005, 35(3)：415-420.

［16］黃衛, 林廣平, 錢振東, 等.正交異性鋼橋面鋪裝層疲勞壽命的斷裂力學分析［J］.土木工程學報, 2006.9, 39(9)：112-116.

［17］張麗芳, 艾軍, 張鵬飛, 等.大跨度鋼箱梁病害及成因分析［J］.公路與汽運, 2013(3) : 203-206.