能量收集無線網絡中面向統計服務質量的最優功率分配

高 雅，張海林，盧小峰

(1.西安電子科技大學 綜合業務網理論及關鍵技術國家重點實驗室，西安 710071； 2.洛陽師范學院 物理與電子信息學院，河南 洛陽 471934)(*通信作者電子郵箱gaoya@stu.xidian.edu.cn)

0 引言

近年來，人們對于高速率數據傳輸業務(例如：視頻會議、視頻電話、高清視頻流等)的需求逐漸增加，使得無線通信系統的能量消耗與日俱增。傳統的無線通信系統主要依靠蓄電池供給能量。然而，這種蓄電池存在著供電時間有限，更換成本高等缺陷，因此，由可再生能源為通信系統提供能量成為一個新的研究熱點[1-2]。由可再生能源轉化為電能存儲到電池中，從而實現可持續供電的過程，被稱為能量收集(Energy Harvesting， EH)過程。基于能量收集的無線通信系統，可以從多元化的能量源中汲取能量，例如：射頻信號、阻尼振動、熱源等[3]。如何合理分配收集的能量成為一個亟待解決的問題。

目前，已經有一些研究成果考慮了基于能量收集無線網絡的功率分配問題[4-9]。文獻[4]以最小化傳輸完成時間為目標，研究了在兩種不同數據到達場景下的功率分配問題；文獻[5]針對靜態信道和衰落信道提出了不同的功率分配方案，得出了該最優功率分配方案為自適應單向注水策略(directional water filling)；文獻[6]提出了在因果隨機狀態信息和完全確定狀態信息兩種情況下的功率分配方案，并得出在因果隨機狀態信息情況下，最優功率分配方案是階梯注水策略(staircase water filling)；文獻[7]以提高能量利用率為目標，研究了在能量收集過程、數據到達過程以及衰落信道統計分布均未知的情況下的動態功率分配與傳輸調度問題。這些成果或是以最大化吞吐量為目標，或是以最小化完成時間為目標來考察在能量受限情況下的最優功率分配。然而，在基于能量收集的5G通信中，高速率數據傳輸業務對時延的敏感性高，這些文獻均未考慮在能量收集無線網絡中如何保障不同通信業務的時延服務質量(Quality of Service, QoS)。盡管文獻[8-9]考慮了在能量收集無線網絡中保障QoS的資源分配問題，但這些文獻僅研究了針對確定性QoS保障下的資源分配，并未考慮對于時延敏感的業務如何保障業務的時延服務質量。

事實上，在5G通信中，高速率數據傳輸業務對時延的要求較高，因此，在基于能量收集的無線網絡中，需要在功率分配的同時保障業務的時延服務質量。Chang[10]依據大偏差理論提出了基于排隊時延的QoS參數。該QoS參數表示受排隊時延影響的指數衰減速率。Wu等[11]依據時延QoS參數提出了在不同QoS需求時的有效容量(Effective Capacity)概念。相比傳統的香農容量，有效容量將傳統的信息理論與統計服務質量保障機制相結合，已經成為衡量5G無線通信網絡的性能指標。近幾年，一些研究成果將時延QoS和有效容量應用于無線通信網絡[10-11]。然而，對于能量收集無線網絡，幾乎沒有文獻考慮業務流的時延受限QoS。針對以上問題和不足，本文提出了基于時延受限QoS的能量收集無線網絡的功率分配方案，以最大化時延QoS約束下的有效容量為目標，以可用功率受限于收集到的能量為約束條件。通過仿真實驗檢驗了本文提出的最優功率分配方案的性能。

1 系統模型

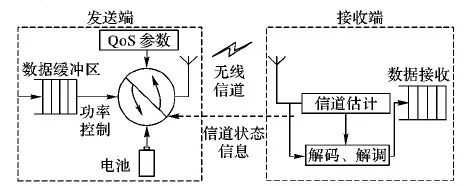
圖1 基于能量收集無線網絡的系統模型

上層數據到達發送端并存儲在數據緩沖區等待發送。發送端的功率控制模塊將依據上層的QoS需求、從接收端反饋的信道狀態信息(Channel State Information, CSI)以及電池的可用能量狀況，自適應地作出功率分配方案，從而最大化QoS約束下的有效容量。假設接收端的信道估計模塊可以準確無誤地對信道狀態進行評估，并將信道狀態信息可靠地反饋給發送端。離散時間信道衰落過程是平穩和各態歷經的，信道功率增益服從平穩的塊衰落信道模型。令第i個時隙瞬時信噪比(Signal-to-Noise Ratio, SNR)記為γ[i]，本文采用了瑞利衰落信道模型，其概率密度函數表示為：

(1)

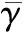
依據大偏差理論[10]，對于穩定的隊列，隊列長度Q的分布可以近似表示為：

Pr{Q>Qth}≈e-θQth

(2)

其中：Qth表示隊列長度界限；參數θ(θ>0)為實數，稱為QoS指數，表示超出時延QoS界限的概率的指數衰減速率。θ越大表示衰減速度越快，相應地，系統對時延的要求也越嚴格；θ越小表示衰減速度越慢，相應地，系統對時延的要求也越松弛。由于無線通信系統中，不同的時延QoS需求對應著不同的θ，可以通過θ從0到∞的取值變化，反映QoS需求從松弛到嚴格的變化。

將系統帶寬記為B，第i個時隙的瞬時傳輸功率記為P[i]，定義序列{R[i],i=1,2,…}為數據服務速率，并表示為：

R[i]=TBlb (1+P[i]γ[i])

(3)

根據文獻[9]，有效容量定義為在指定QoS約束的情況下，服務過程所能支持的最大到達速率。如果數據服務速率序列是平穩和時間不相關的，那么有效容量可以記為：

(4)

實際通信系統中，QoS指數與有效容量、帶寬等密切相關。針對不同的通信系統，具體的QoS指數可唯一得出。

2 面向統計QoS的功率分配問題

2.1 問題描述

在能量收集無線通信網絡中，在可用功率受限于收集到的能量的情況下，最大化有效容量的模型可以表示如下。

問題1

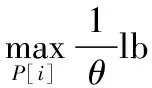
(5)

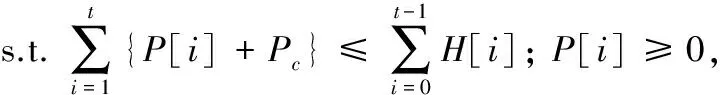
(6)

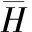
2.2 凸問題轉化

在最優化問題1中，可以看出目標函數是對γ求積分，而約束條件是對時間t求和。為了求解問題1，將約束條件(6)轉化為：

(7)

事實上，式(6)與式(7)是等價的。這是由于能量收集過程是平穩和各態歷經的，因此，式(6)中功率消耗和能量收集的時間平均與式(7)中的統計平均相等[12]，即：

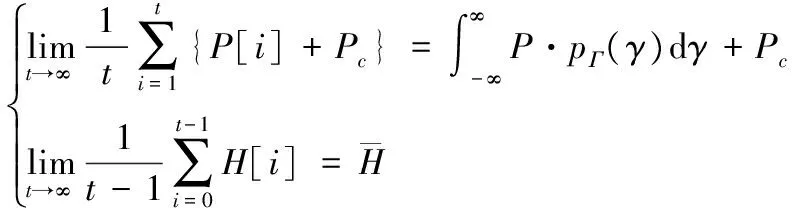
(8)

把約束條件(6)轉化為約束條件(7)是將充電時間擴大之后的結果，這在實際通信系統中也是合理的。這是由于能量收集無線網絡的發送端通常需要在首次發送數據包之前充電一段時間，因此，長時間的統計平均更符合實際的通信系統，更具有現實意義。在下文中，為了表達簡便將省去時間指代i。

在問題1的目標函數中，由于log函數是單調遞增的，因此原問題可以簡化為一個新的問題2。

問題2

(9)

(10)

可以看出，問題2是關于P的嚴格凸的最優化問題，并與問題1等價。

2.3 問題的求解

根據凸優化理論[13]，最優化問題2的Lagrangian函數可以表示為：

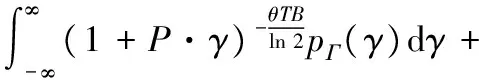
(11)

其中ρ為拉格朗日乘子。問題2的Karush-Kuhn-Tucker (KKT)條件可以表示為：

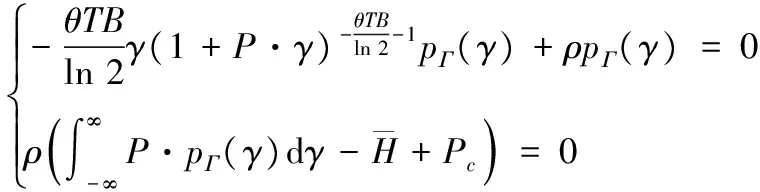
(12)

記γth=ρln 2/(θTB)，求解式(12)，可以得到定理1如下所示。

定理1 面向統計QoS保障的能量收集無線網絡的最優功率分配方案為：

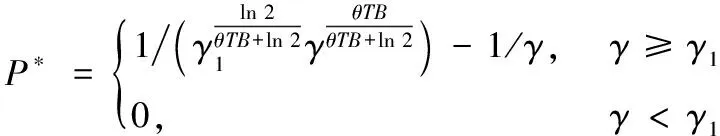
(13)

其中γ1是信噪比中斷門限，可以通過將式(13)代入式(14)中求解得到γ1。

(14)

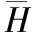
引理1 當QoS需求非常松弛(θ→0)時，最優功率分配方案收斂于注水策略；當QoS需求非常嚴格(θ→∞)時，最優功率分配方案收斂于信道反轉機制。即功率分配與信道狀態成反比。

證明 為了證明引理1，將在如下兩種情況下討論最優功率分配方案。

1)θ→0。

將θ=0代入式(13)，可以得出當QoS需求非常松弛時的最優功率分配方案，如下所示：

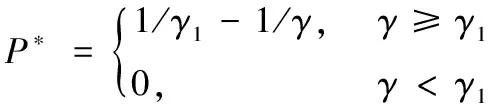
(15)

從式(15)可以看出，在QoS需求非常松弛時的最優功率分配方案為注水策略。

2)θ→∞。

根據式(13)，QoS需求非常嚴格時的最優功率分配方案可以表示為：

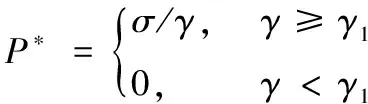
(16)

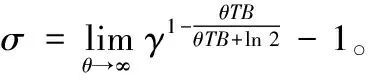
將式(13)代入式(4)，便可求出在最優功率分配方案下的最大有效容量的閉式解，如下所示：

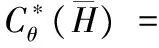
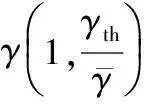
(17)

其中Γ(·,·)和γ(·,·)為兩個不完全伽馬函數。

3 中斷概率分析

無線通信網絡中，業務流有支持其發送的最小數據速率，記為Rth。由于路徑損耗和陰影衰落等信道特性，會使得發送端的發送速率無法滿足支持業務流所需要的該最小數據速率，從而產生中斷，因此，在基于能量收集的無線通信網絡中，可以通過分析本文提出的最優功率分配方案下的信道中斷概率來評價所提出最優功率分配方案的性能。令Pout表示信道中斷概率，則由文獻[14-15]可知，最優功率分配方案下的信道中斷概率可以表示為：

Pout=Pr{R≤Rth}=Pr{TBlb (1+P*·γ)≤Rth}=

(18)

其中R0=Rth/TB表示歸一化后的業務流最小支持速率，它與幀長和帶寬無關，僅與發送功率和信道狀態有關；z表示信道的加性高斯白噪聲。由式(18)可知，信道中斷概率可以表示為信噪比小于門限(2Rth/TB-1)/P*的概率。將最優功率分配方案代入式(18)，可以得到：

(19)

觀察式(19)，可以得出QoS需求、信道狀態與信道中斷概率的關系，如引理2所述。

引理2 當QoS需求非常松弛(θ→0)時，所提出的最優功率分配方案下的信道中斷概率在低信噪比區域趨近于1，高信噪比區域趨近于0。當QoS需求非常嚴格(θ→∞)時，所提出的最優功率分配方案下的信道中斷概率在低信噪比區域趨近于0，高信噪比區域趨近于1。

引理2的證明可以由式(19)分別取θ=0和θ=∞兩種特例中獲得，故不再證明。

4 仿真分析

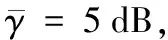
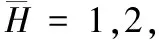
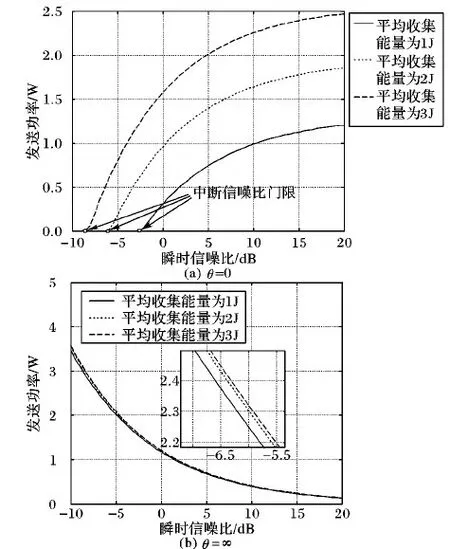
圖2 不同θ值時的最優功率分配方案

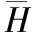
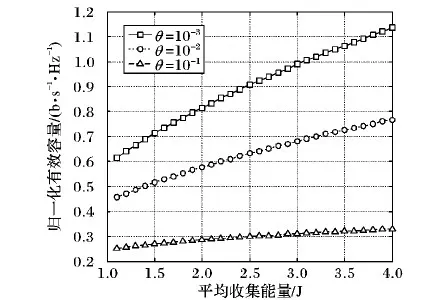
圖3 有效容量隨平均收集能量的變化

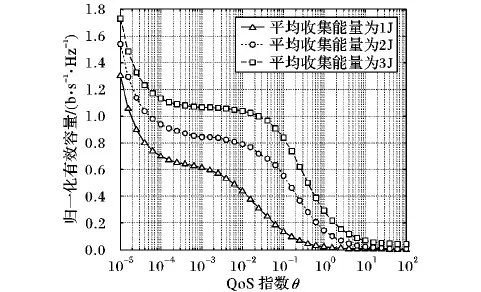
圖4 有效容量隨QoS指數θ的變化

為了將本文提出的最優功率分配方案與現有的算法進行比較，圖5分別給出了本文提出的最優功率分配方案、注水策略、信道反轉策略和恒定功率分配下的有效容量隨QoS指數變化的曲線。從圖5可以看出，本文提出的最優功率分配方案下的有效容量隨著QoS指數的增大而減小。當QoS指數非常小時，最優功率分配方案收斂于注水策略；當QoS指數非常大時，最優功率分配方案收斂于信道反轉策略。同時，相比注水策略、信道反轉策略和恒定功率分配策略，本文提出的最優功率分配方案可以獲得最大的有效容量，從而驗證了本文提出的最優功率分配方案具有較好的系統性能。

為了評估文章提出的最優功率分配方案下的信道中斷概率，圖6分別給出了當QoS指數非常小(θ=10-5)和QoS指數非常大(θ=1)時的信道中斷概率隨瞬時SNR變化的曲線。

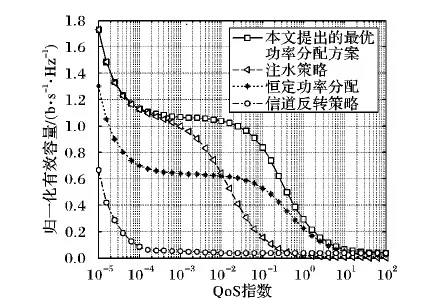
圖5 幾種方案有效容量隨QoS指數變化

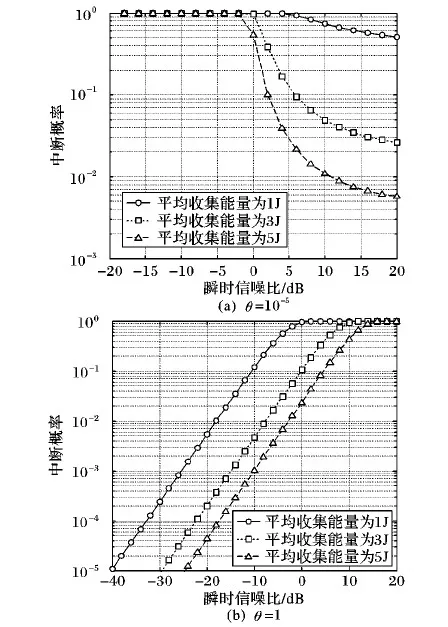
圖6 不同θ值時的中斷概率對比

5 結語

本文提出了基于QoS的能量收集無線通信網絡中的最優功率分配方案，從而在給定時延QoS約束下最大化有效容量。首先，建立了最優化模型，并求解出了最優功率分配方案的閉式解。通過分析，本文得出了隨著QoS指數從0到∞變化，最優功率分配方案在注水策略和信道反轉策略之間變化，并通過求解信道中斷概率理論檢驗了最優功率方案的性能。仿真實驗表明，相比現有的功率分配方案，本文提出的最優功率分配方案能獲得更大的有效容量。

References)

[1] SUDEVALAYAM S, KULKAMI P. Energy harvesting sensor nodes: survey and implications [J]. IEEE Communications Surveys Tutorials, 2011, 13 (3): 443-461.

[2] WU D, HE J, WANG H, et. al. A hierarchical packet forwarding mechanism for energy harvesting wireless sensor networks [J]. IEEE Communications Magazine, 2015, 53(8): 92-98.

[3] 趙爭鳴，王旭東.電磁能量收集技術現狀及發展趨勢[J].電工技術學報，2015,30(13)：1-11.(ZHAO Z M, WANG X D. The state of art and the future trend for the energy harvesting technology [J]. Transactions of China Electrotechnical Society, 2015, 30(13): 1-11.)

[4] YANG J, ULUKUS S. Optimal packet scheduling in an energy harvesting communication system [J]. IEEE Transactions on Communications, 2012, 60 (1): 220-230.

[5] OZEL O, TUTUNCUOGLU K, YANG J, et al. Transmission with energy harvesting nodes in fading wireless channels: optimal policies [J]. IEEE Journal on Selected Areas in Communications, 2011, 29(8): 1732-1743.

[6] HO C K, ZHANG R. Optimal energy allocation for wireless communications with energy harvesting constraints [J]. IEEE Transactions on Signal Processing, 2012, 60, (9): 4808-4818.

[7] 劉迪迪，林基明，王俊義，等.混合供電發射機的功率分配及調度算法[J].西安電子科技大學學報(自然科學版),2016，43(6)：8-14.(LIU D D, LIN J M, WANG J Y, et. al. Power allocation and transmission scheduling for a transmitter with hybrid energy sources [J]. Journal of Xidian University (Natural Science), 2016, 43(6): 8-14.)

[8] LOODARICHEH R A, MALLICK S, BHAGAVA V K. Resource allocation with QoS provisioning for energy harvesting systems: a goal programming approach [C]// Proceedings of 2015 IEEE International Conference on Communications. Piscataway, NJ: IEEE, 2015: 2791-2796.

[9] LIU G, WANG Z, JIANG T. QoS-aware throughput maximization in wireless powered underground sensor networks [J]. IEEE Transactions on Communications, 2016, 64(11): 4776-4789.

[10] CHANG C S. Stability, queue length, and delay of deterministic and stochastic queuing networks [J]. IEEE Transactions on Automatic Control, 1994, 39(5): 913-931.

[11] WU D, NEGI R. Effective capacity: a wireless link model for support of quality of service [J]. IEEE Transactions on Wireless Communications, 2003, 2(4): 630-643.

[12] CINLAR E. Introduction to Stochastic Processes [M]. Upper Saddle River: Prentice-Hall, 1975: 10-12.

[13] BOYD S, VANDENBERGHE L. Convex Optimization [M]. Cambridge: Cambridge University Press, 2004: 42-45.

[14] ZHOU S, CHEN T, CHEN W, et. al. Outage minimization for a fading wireless link with energy harvesting transmitter and receiver [J]. IEEE Journal on Selected Areas in Communications, 2015, 33(3): 496-511.

[15] TSE D, VISWANATH P. Fundamentals of Wireless Communication [M]. Cambridge: Cambridge University Press, 2005: 112-114.

This work is partially supported by the National Natural Science Foundation of China (61371127, 61671347), the Program of Introducing Talents of Discipline to Universities (B08038), the Natural Science Foundation of Shaanxi Province (2016JQ6027), the Fundamental Research Funds for the Central Universities (7214603701), the Key Technology R&D Program of Henan Province (142102210572).

GAOYa, born in 1985, Ph. D. candidate, lecturer. Her research interests include quality of service guarantees of wireless network, energy harvesting network, cognitive radio network, convex optimization theory.

ZHANGHailin, born in 1964, Ph. D., professor. His research interests include broadband wireless network, 5G communications technologies.

LUXiaofeng, born in 1974, Ph. D., associate professor. His research interests include wireless signal processing, 5G communications technologies.