基于對偶四元數(shù)的慣性/衛(wèi)星/天文組合導(dǎo)航系統(tǒng)改進聯(lián)邦濾波方法

閔艷玲， 熊智， 邢麗， 劉建業(yè)， 殷德全

(南京航空航天大學(xué) 自動化學(xué)院, 江蘇 南京 211100)

0 引言

捷聯(lián)慣性導(dǎo)航系統(tǒng)不需要接收任何外界信息，僅依靠陀螺和加速度計的測量輸出即可解算出載體的速度、位置、姿態(tài)等運動參數(shù)，具有抗干擾能力強、隱蔽性好、導(dǎo)航信息完整和數(shù)據(jù)更新率高等優(yōu)點，但慣性解算屬于積分解算，因此其導(dǎo)航誤差隨時間累積，難以滿足運動載體長時間高精度的導(dǎo)航需求[1]。

衛(wèi)星導(dǎo)航系統(tǒng)定位精度高，導(dǎo)航誤差不隨時間累積，但其信號易受干擾，且在有遮擋的環(huán)境中容易發(fā)生信號丟失或?qū)Ш秸`差變大[2]。天文導(dǎo)航系統(tǒng)利用天文敏感器測得天體的方位信息，從而得到運動載體的姿態(tài)參數(shù)，具有自主性強、姿態(tài)測量精度高、誤差不隨時間累積的優(yōu)點，但也易受到環(huán)境干擾[3]。根據(jù)慣性導(dǎo)航系統(tǒng)、衛(wèi)星導(dǎo)航系統(tǒng)、天文導(dǎo)航系統(tǒng)的特點進行有效組合，構(gòu)成慣性/衛(wèi)星/天文組合導(dǎo)航系統(tǒng)，可對慣性導(dǎo)航系統(tǒng)中的各誤差項進行補償，從而實現(xiàn)高精度導(dǎo)航。目前，慣性/衛(wèi)星/天文組合導(dǎo)航系統(tǒng)已成為中遠程彈道導(dǎo)航、高空長航時飛行器、空天飛行器中最有效的高性能導(dǎo)航手段[3]。

文獻[4]在姿態(tài)組合過程中，將天文導(dǎo)航輸出的機體相對于慣性坐標(biāo)系的姿態(tài)轉(zhuǎn)化為相對于地理坐標(biāo)系的姿態(tài)，轉(zhuǎn)化時耦合了慣性導(dǎo)航系統(tǒng)的位置誤差，影響狀態(tài)量估計精度，未能最大限度地使用天文導(dǎo)航所提供的高精度姿態(tài)信息；文獻[5]針對上述轉(zhuǎn)化過程中的耦合誤差問題，首先在慣性系中利用天文導(dǎo)航輸出對陀螺誤差進行估計和補償，再在地理系下進行位置組合，其中姿態(tài)組合濾波器采用了開環(huán)結(jié)構(gòu)，長時間運行存在發(fā)散風(fēng)險；文獻[2]和文獻[4]采用聯(lián)邦濾波器進行慣性/衛(wèi)星/天文組合導(dǎo)航系統(tǒng)的信息融合，主濾波器與各子濾波器狀態(tài)保持一致，因此慣性/天文子濾波器中包含了不可觀測狀態(tài)量；文獻[6]提出了基于對偶四元數(shù)的慣性/天文組合導(dǎo)航算法，但同樣忽略了狀態(tài)的可觀測性問題。

針對上述問題，本文提出了基于對偶四元數(shù)的慣性/衛(wèi)星/天文組合、導(dǎo)航系統(tǒng)改進聯(lián)邦濾波方法，利用基于奇異值分解的可觀測性分析方法建立子濾波器，有效地減少濾波計算量。基于對偶四元數(shù)的降維慣性/天文組合方法，直接利用天文信息進行慣性系姿態(tài)組合，再將慣性系姿態(tài)轉(zhuǎn)換為地理系姿態(tài)。相較于傳統(tǒng)慣性/天文采用地理系姿態(tài)組合的方法，對偶四元數(shù)慣性/天文組合方法受慣性導(dǎo)航位置誤差影響較小，具有更高的組合精度。因此，基于對偶四元數(shù)的慣性/衛(wèi)星/天文改進聯(lián)邦濾波方法可以有效地提高慣性/衛(wèi)星/天文組合導(dǎo)航系統(tǒng)性能，并為其工程化應(yīng)用提供參考。

1 對偶四元數(shù)慣性導(dǎo)航誤差模型

1.1 坐標(biāo)系定義

e表示地球坐標(biāo)系，原點在地心，一個軸與地軸重合，其他兩個軸在赤道面。

i表示慣性坐標(biāo)系，0時刻與地球坐標(biāo)系重合。

b表示載體坐標(biāo)系，即捷聯(lián)慣性器件的坐標(biāo)系，原點在加速度計三元組的質(zhì)心，3個坐標(biāo)軸分別與加速度計敏感軸重合，構(gòu)成右手正交系。

t表示推力速度坐標(biāo)系，與載體坐標(biāo)系平行，從地心到坐標(biāo)原點的向量等于推力速度。

g表示引力速度坐標(biāo)系，與地球坐標(biāo)系平行，從地心到坐標(biāo)原點的向量等于引力速度。

u表示位置坐標(biāo)系，與地球坐標(biāo)系平行，從地心到坐標(biāo)原點的向量等于載體的位置向量。

1.2 誤差模型

對偶四元數(shù)定義為

(1)

式中：q和q′分別為對偶四元數(shù)的標(biāo)量和對偶部分，都是普通四元數(shù)；ε2=0，但ε≠0.

對偶四元數(shù)的加性誤差定義為

(2)

式中：qo為對偶四元數(shù)計算值或量測值；q為真實值。

陀螺誤差δωbib和加速度計誤差δfb均建模為常值誤差與高斯白噪聲隨機誤差的線性組合：

(3)

式中：δωbibc為陀螺常值漂移；δωbibs為陀螺隨機白噪聲；δfbc為加速度計常值誤差；δfbs為加速度計隨機白噪聲。

文獻[6-7]對基于加性對偶四元數(shù)的捷聯(lián)慣性導(dǎo)航算法誤差方程進行了詳細推導(dǎo)，此處不再贅述。

推力對偶四元數(shù)qit=qit+εq′it刻畫了推力速度坐標(biāo)系t相對于慣性坐標(biāo)系i的一般性剛體運動，其誤差方程為

(4)

式中：fb和ωbib分別是加速度計和陀螺輸出值；°為四元數(shù)乘子。

引力對偶四元數(shù)qig=qig+εq′ig刻畫了引力速度坐標(biāo)系g相對于慣性坐標(biāo)系i的一般性剛體運動，其誤差方程為

(5)

式中：ωeie為地球自轉(zhuǎn)角速度。

位置對偶四元數(shù)qiu=qiu+εq′iu刻畫了位置坐標(biāo)系u相對于慣性坐標(biāo)系i的一般性剛體運動，其誤差方程為

(6)

(7)

式中：q*iu、q*it、q*ig分別為qiu、qit、qig的共軛四元數(shù)。

1.3 狀態(tài)方程

為了方便進行四元數(shù)計算，δωbibc、δfbc均表示為標(biāo)量部分為0的四元數(shù)，將其矢量部分分別表示為δΩbibc、δFbc并擴充到狀態(tài)量中，可將文獻[6]中的24維狀態(tài)量簡化到22維；δωbibs、δfbs同樣也可將為0的標(biāo)量部分剔除，僅將其矢量部分δΩbibs、δFbs作為噪聲向量，則噪聲向量由8維簡化到6維，狀態(tài)方程也可相應(yīng)地進行簡化。

由(3)式～(6)式，可建立如下狀態(tài)方程：

(8)

式中：X∈R22×1為狀態(tài)向量，

(9)

F∈R22×22為狀態(tài)轉(zhuǎn)移矩陣；G∈R22×6為噪聲驅(qū)動陣；w∈R6×1為噪聲向量，

(10)

當(dāng)四元數(shù)寫成4維向量q=[s,vT]T時，s為其標(biāo)量部分，向量部分v=[v1v2v3]，四元數(shù)乘法[7]可以表示為

(11)

兩個矩陣[q]+和[q]-定義為

(12)

式中：I3為3維單位矩陣；[v×]為向量v生成的反對稱矩陣，

(13)

為簡化矩陣表示，設(shè)存在矩陣T，M(T)表示去除T矩陣第1列后的矩陣。

因此，(8)式中的F陣可表示為

(14)

(8)式中的G陣可表示為

(15)

1.4 量測方程

1.4.1 慣性/衛(wèi)星子導(dǎo)航系統(tǒng)

根據(jù)對偶四元數(shù)捷聯(lián)慣性導(dǎo)航算法的特點，選擇慣性坐標(biāo)系i中的速度誤差和地球坐標(biāo)系e中的位置誤差作為量測向量。對偶四元數(shù)算法解算得到的慣性系速度Vi及地球系位置Re為

(16)

(17)

由于慣性系在1.1節(jié)中定義為0時刻的地球系，即δqig(0)=δqiu(0)=0，且由文獻[7]可知：

(18)

δVi=2(δq′it°q*it-q′it°q*it°δqit°q*it+
δq′ig°q*ig)，

(20)

(21)

由于衛(wèi)星導(dǎo)航系統(tǒng)所測得的速度和位置均為地球坐標(biāo)系參數(shù)，因此需利用衛(wèi)星的速度測量信息VeGNSS計算載體的慣性系速度ViGNSS. 由速度合成定理及坐標(biāo)系旋轉(zhuǎn)可得

(22)

式中：Cie表示地球系到慣性系的坐標(biāo)旋轉(zhuǎn)矩陣；Vie表示地球系與慣性系之間的相對速度，可通過地球自轉(zhuǎn)角速度和衛(wèi)星導(dǎo)航系統(tǒng)測得的載體位置簡單計算得到。由于地球自轉(zhuǎn)角速度較小，且衛(wèi)星導(dǎo)航系統(tǒng)的位置測量誤差也是小量，因此可以忽略Vie的誤差。在此條件下，設(shè)δVeGNSS為衛(wèi)星導(dǎo)航系統(tǒng)的地球系速度測量誤差，則衛(wèi)星導(dǎo)航系統(tǒng)的慣性系速度測量誤差δViGNSS=CieδVeGNSS. 地球自轉(zhuǎn)角速度的四元數(shù)表示為ωeie=[000ωie]，利用標(biāo)量ωie計算可得Cie，

(23)

由于對偶四元數(shù)慣性導(dǎo)航算法解算得到的慣性系速度Vi及地球系位置Re均為標(biāo)量部分為0的四元數(shù)，因此只取其矢量部分與衛(wèi)星導(dǎo)航系統(tǒng)測量值的差值作為量測量。由(20)式、(21)式可得慣性、衛(wèi)星子導(dǎo)航系統(tǒng)量測方程為

(24)

式中：Z1∈R6×1為量測向量；H1∈R6×22為系統(tǒng)量測矩陣；V1∈R6×1為系統(tǒng)量測噪聲向量，

(25)

nV∈R3×1為衛(wèi)星導(dǎo)航系統(tǒng)計算得到的慣性系速度量測噪聲，nR∈R3×1為衛(wèi)星導(dǎo)航系統(tǒng)的位置量測噪聲。

設(shè)U(T)表示去除矩陣T的第1行，則系統(tǒng)量測矩陣H1可表示為

(26)

1.4.2 慣性/天文子導(dǎo)航系統(tǒng)

天文敏感器的輸出信息為載體坐標(biāo)系b相對于慣性系i的旋轉(zhuǎn)四元數(shù)qcns，對偶四元數(shù)捷聯(lián)慣性導(dǎo)航算法解算得到的qit為推力速度坐標(biāo)系t相對于慣性坐標(biāo)系i的旋轉(zhuǎn)四元數(shù)。從坐標(biāo)系的定義可知，推力坐標(biāo)系t與載體坐標(biāo)系b平行。因此不需要進行轉(zhuǎn)換，即可將二者差值作為量測量。

慣性/天文子導(dǎo)航系統(tǒng)的量測方程為

(27)

式中：Z2∈R4×1為量測向量；V2∈R4×1為系統(tǒng)量測噪聲向量；H2∈R4×22為系統(tǒng)量測矩陣，

(28)

2 基于可觀測性分析的改進聯(lián)邦濾波器設(shè)計

2.1 基于奇異值分解的可觀測性分析方法

由1.3節(jié)可知，全狀態(tài)量的維數(shù)為22，組合導(dǎo)航系統(tǒng)一般采用卡爾曼濾波器進行信息融合，其計算時間主要由系統(tǒng)狀態(tài)維數(shù)n和量測維數(shù)m決定，每一個濾波周期的計算量與(n3+mn2)呈正比[8]。如果系統(tǒng)的維數(shù)較高，會增加濾波器計算量，導(dǎo)致導(dǎo)航系統(tǒng)的實時性變差。因此在保證導(dǎo)航精度的前提下，提高系統(tǒng)的實時性，具有重要的研究意義。

假設(shè)某動態(tài)系統(tǒng)進行分段線性處理后，各時間段內(nèi)的系統(tǒng)狀態(tài)轉(zhuǎn)移矩陣為Φj(j=1,2,…)，量測矩陣為Hj. 對該動態(tài)系統(tǒng)，設(shè)在第j個時間段內(nèi)的可觀測性矩陣為Nj，則

(29)

設(shè)時間段個數(shù)為λ，則總時間內(nèi)系統(tǒng)的可觀測性矩陣N(l×n維)為

(30)

對其進行奇異值分解得

(31)

式中：U=[u1u2…ul]；V=[v1v2…vn]為正交矩陣；S=[Λr×r0

00]，Λr×r=diag(σ1σ2…σr)，r、σi(i=1,2,…,r)分別為N的秩和非零奇異值。

奇異值σi是與其對應(yīng)的右奇異向量vi中取得最大絕對值的狀態(tài)所對應(yīng)的奇異值[9]。奇異值的個數(shù)即矩陣N的秩r，決定了可觀測狀態(tài)量的個數(shù)。

2.2 子濾波器狀態(tài)變量可觀測性分析

由于不同的機動情況對狀態(tài)量的觀測性會有所影響，因此分別選擇了勻速機動、加速機動、橫滾機動、俯仰機動、航向機動這5種常見的機動方式對各狀態(tài)量的可觀測性情況進行分析。每次仿真時間為5 s，時間間隔為0.02 s，各機動方式的仿真參數(shù)如表1所示。

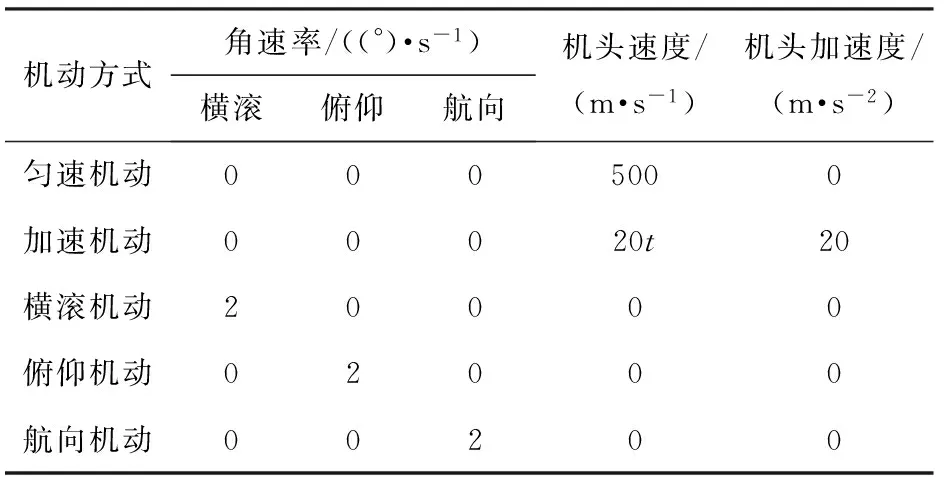
表1 機動參數(shù)設(shè)置

根據(jù)上述仿真條件進行基于奇異值分解的可觀測性分析，發(fā)現(xiàn)在5種機動情況下，慣性/衛(wèi)星子導(dǎo)航系統(tǒng)中可觀測性矩陣的秩均為22，但不同的機動情況下各狀態(tài)量的奇異值相對大小不同。這表明慣性/衛(wèi)星子導(dǎo)航系統(tǒng)對所有狀態(tài)均具有可觀測性，但不同機動條件下各狀態(tài)量的可觀測度不同。由于本文主要關(guān)注狀態(tài)量是否是可觀測的，因此慣性/衛(wèi)星子濾波器不需進行降維。

慣性/天文子導(dǎo)航系統(tǒng)在5種機動情況下可觀測性矩陣的秩均為7，可觀測的7個狀態(tài)量包括四元數(shù)δqit以及三維矢量δΩbibc，但同樣在不同機動條件下各狀態(tài)量的可觀測度不同。由此可知，可對慣性/天文子濾波器進行降維。

2.3 降維慣性/天文子濾波器

2.3.1 狀態(tài)方程

降維慣性/天文子導(dǎo)航系統(tǒng)的狀態(tài)方程為

(32)

式中：X2∈R7×1為狀態(tài)向量，

(33)

F2∈R7×7為狀態(tài)轉(zhuǎn)移矩陣，

(34)

G2∈R7×3為噪聲驅(qū)動陣，

(35)

w2=δΩbibs為3維噪聲向量。

2.3.2 量測方程

降維后，慣性/天文子導(dǎo)航系統(tǒng)的量測方程為

(36)

式中：量測向量Z2與量測噪聲向量V2未發(fā)生變化，僅由于狀態(tài)變量變?yōu)閄2，導(dǎo)致系統(tǒng)量測矩陣由H2變?yōu)镠3，H3∈R4×7，

(37)

2.3.3 計算量對比

濾波計算量與(n3+mn2)呈正比，表2為降維前后的計算量對比。

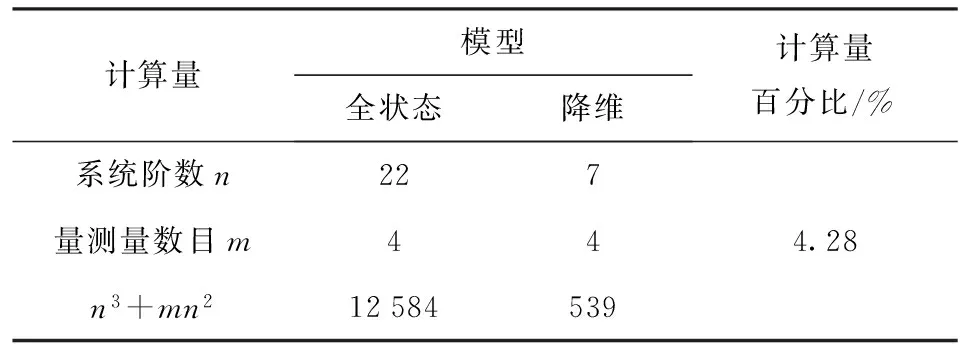
表2 慣性/天文子濾波器計算量對比

由表2可知，與文獻[6]中濾波器的計算量相比，降維后的計算量僅為其4.28%，計算量得到大量簡化。

2.4 改進聯(lián)邦濾波器設(shè)計

本文聯(lián)邦濾波器中的主濾波器采用22維全狀態(tài)變量，慣性/衛(wèi)星子導(dǎo)航系統(tǒng)中由于狀態(tài)全部可觀，因此與主濾波器保持一致，狀態(tài)方程與量測方程如1.3節(jié)、1.4節(jié)所示。慣性/天文子導(dǎo)航系統(tǒng)僅使用部分狀態(tài)變量，狀態(tài)方程與量測方程如2.3節(jié)所示。本文采用了有重置的聯(lián)邦濾波結(jié)構(gòu)，利用全局估計值對對偶四元數(shù)慣導(dǎo)系統(tǒng)進行閉環(huán)反饋修正，結(jié)構(gòu)圖如圖1所示。

主濾波器全局狀態(tài)空間到慣性/衛(wèi)星子濾波器局部狀態(tài)空間的映射矩陣T1=I22，到慣性/天文子濾波器局部狀態(tài)空間的映射矩陣T2為

(38)

全局融合估計值[10]可表示為

(39)

信息分配過程為

(40)

式中：βi=12；k表示當(dāng)前時刻。

3 仿真驗證

3.1 仿真條件設(shè)置

各導(dǎo)航傳感器參數(shù)設(shè)置如表3所示，慣性導(dǎo)航解算周期為0.02 s，濾波周期為1 s，仿真時長為800 s，導(dǎo)航坐標(biāo)系為“北天東”地理坐標(biāo)系。

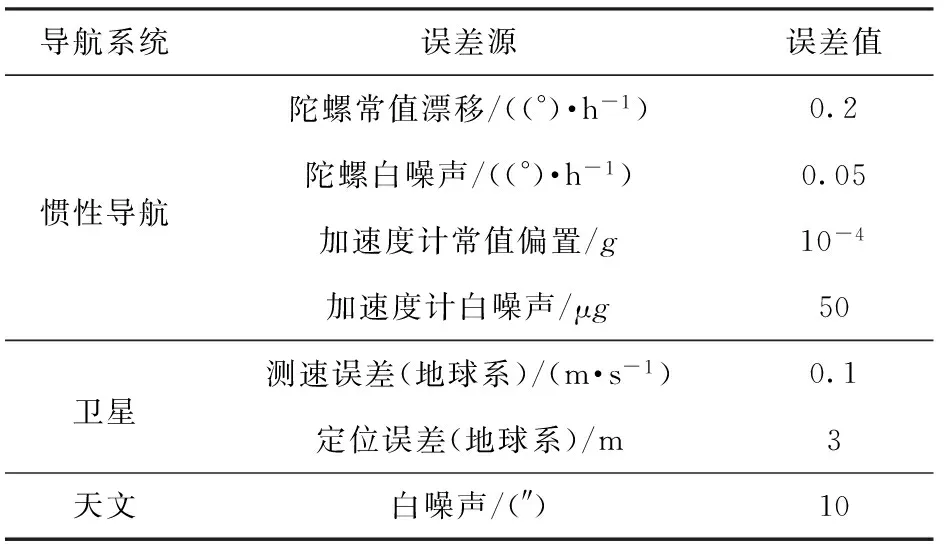
表3 傳感器參數(shù)設(shè)置

3.2 基于對偶四元數(shù)的慣性/衛(wèi)星/天文組合導(dǎo)航系統(tǒng)改進聯(lián)邦濾波仿真驗證

3.2.1 方法有效性驗證

1)動態(tài)航跡設(shè)計

為了驗證所設(shè)計的基于對偶四元數(shù)的慣性/衛(wèi)星/天文改進聯(lián)邦濾波方法性能，設(shè)計了一組姿態(tài)、速度變化的動態(tài)航跡，該航跡主要用于驗證算法的有效性。

橫滾角(°)、航向角(°)、俯仰角(°)和機頭速度vb(m/s)隨時間t的變化規(guī)律為：γ=ψ=θ=-0.000 18t2+0.18t，vb=-0.000 8t2+1.5t.

2)有效性仿真驗證

根據(jù)3.1節(jié)中的仿真設(shè)置條件，對基于對偶四元數(shù)的慣性/衛(wèi)星/天文改進聯(lián)邦濾波進行了仿真分析，導(dǎo)航誤差曲線如圖2所示。由于當(dāng)各子濾波器與主濾波器維數(shù)相同時，其全局濾波和集中式卡爾曼濾波等價[11]，因此還對基于對偶四元數(shù)的慣性/衛(wèi)星/天文集中式卡爾曼濾波進行了導(dǎo)航仿真驗證，其導(dǎo)航仿真誤差曲線如圖3所示。

觀察圖2及表4中改進聯(lián)邦濾波方法的導(dǎo)航誤差統(tǒng)計可知，改進后的聯(lián)邦濾波方法可獲得高精度的導(dǎo)航信息，為飛行器提供可靠的位置、速度、姿態(tài)數(shù)據(jù)。對比圖2、圖3以及表4中改進聯(lián)邦濾波與集中式卡爾曼濾波導(dǎo)航誤差的統(tǒng)計數(shù)據(jù)可以發(fā)現(xiàn)，改進聯(lián)邦濾波的精度略低于集中式卡爾曼濾波，但是差別很小，誤差位于同一數(shù)量級。這是由于改進聯(lián)邦濾波中慣性/天文子濾波器維數(shù)與主濾波器不一致，因此損失了部分信息，屬于次優(yōu)濾波[11]。但是從表2中的計算量對比可知，改進聯(lián)邦濾波方法的計算量得到大量的簡化，鑒于改進后聯(lián)邦濾波器的實時性優(yōu)勢，較小的精度損失是可以承受的。

傳統(tǒng)的慣性/衛(wèi)星/天文聯(lián)邦濾波將地理系位置、地理系速度、地理系下定義的平臺誤差角、加速度計誤差和陀螺誤差作為狀態(tài)量，且慣性/衛(wèi)星與慣性/天文子濾波器狀態(tài)方程保持一致。本文中基于對偶四元數(shù)的降維慣性/天文子濾波器直接利用天文信息進行組合，不需要將其轉(zhuǎn)化到地理系。由于在衛(wèi)星導(dǎo)航系統(tǒng)完好的情況下，慣性導(dǎo)航位置誤差較小，基于對偶四元數(shù)的降維慣性/天文組合優(yōu)勢不明顯。為體現(xiàn)本文中慣性/天文組合方法的優(yōu)勢，考慮衛(wèi)星導(dǎo)航系統(tǒng)由于故障等原因已進行隔離，僅余慣性/天文子濾波器的情況。在3.1節(jié)的仿真條件下，將基于對偶四元數(shù)的降維慣性/天文組合導(dǎo)航方法與傳統(tǒng)慣性/天文組合導(dǎo)航方法進行對比，導(dǎo)航誤差對比曲線如圖4所示，陀螺常值漂移估計曲線如圖5、圖6所示。

圖4中虛線表示傳統(tǒng)慣性/天文組合導(dǎo)航誤差，實線表示基于對偶四元數(shù)的降維慣性/天文組合導(dǎo)航誤差。從表5可知，傳統(tǒng)慣性/天文組合模式姿態(tài)精度優(yōu)于純慣性導(dǎo)航，但是速度和位置精度卻較低。這是由于在傳統(tǒng)慣性/天文組合模式中位置誤差、速度誤差、加速度計誤差均作為狀態(tài)量進行卡爾曼濾波估計，但這些狀態(tài)量可觀測性較低或不具有可觀測性，將這些狀態(tài)量反饋并進行慣性導(dǎo)航誤差修正，反而可能會降低慣性導(dǎo)航位置、速度精度。基于對偶四元數(shù)的降維慣性/天文組合相比于純慣性導(dǎo)航在姿態(tài)、速度、位置(三維矢量和)上均有所提升。該組合模式中僅包含可觀的狀態(tài)量，且直接與天文姿態(tài)進行組合，因而具有較好的姿態(tài)精度，從而獲得了更好的位置和速度精度，具有更優(yōu)的導(dǎo)航性能，但是由于位置、速度誤差缺少修正，因此位置和速度仍呈發(fā)散趨勢。

表4 基于對偶四元數(shù)的慣性/衛(wèi)星/天文導(dǎo)航誤差均方根值統(tǒng)計(有效性驗證)

Tab.4 RMS statistics of navigation errors of SINS/GNSS/CNS based on dual quaternions (effectiveness simulation)

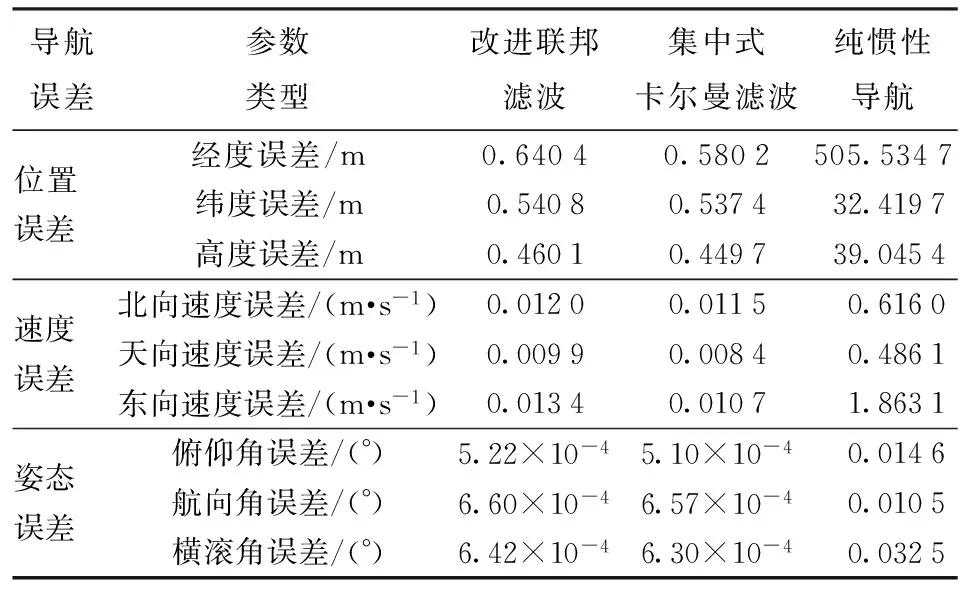
導(dǎo)航誤差參數(shù)類型改進聯(lián)邦濾波集中式卡爾曼濾波純慣性導(dǎo)航位置經(jīng)度誤差/m0.64040.5802505.5347誤差緯度誤差/m0.54080.537432.4197高度誤差/m0.46010.449739.0454速度北向速度誤差/(m·s-1)0.01200.01150.6160誤差天向速度誤差/(m·s-1)0.00990.00840.4861東向速度誤差/(m·s-1)0.01340.01071.8631姿態(tài)俯仰角誤差/(°)5.22×10-45.10×10-40.0146誤差航向角誤差/(°)6.60×10-46.57×10-40.0105橫滾角誤差/(°)6.42×10-46.30×10-40.0325

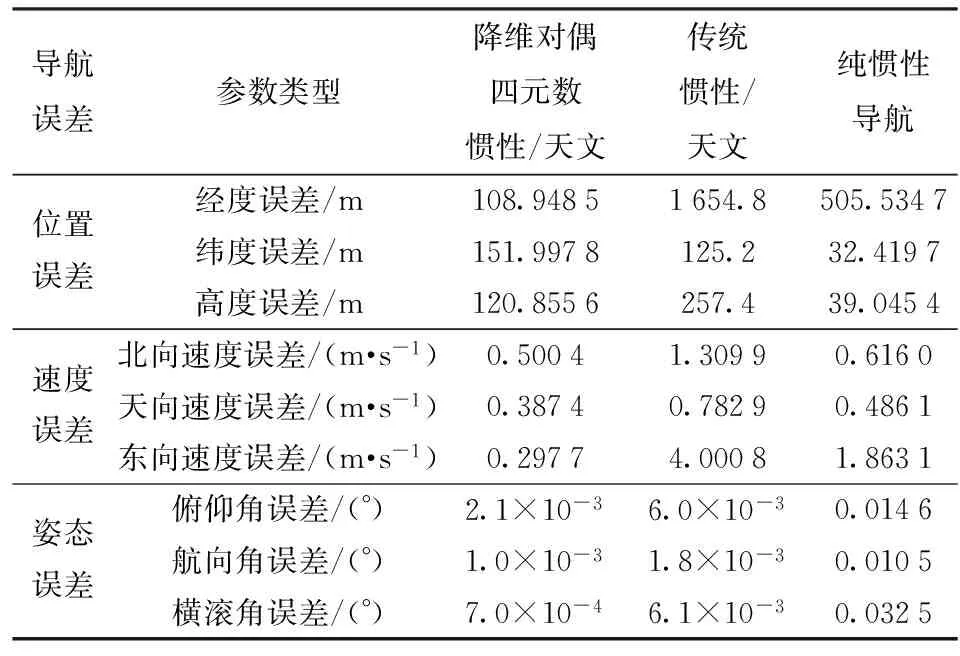
表5 慣性/天文導(dǎo)航誤差均方根值統(tǒng)計(有效性驗證)

觀察圖4以及對比表5中的誤差統(tǒng)計數(shù)據(jù)，可以發(fā)現(xiàn)基于對偶四元數(shù)的降維慣性/天文組合相比于傳統(tǒng)慣性/天文組合具有更高的姿態(tài)精度。對比圖5、圖6可知，對偶四元數(shù)慣性/天文組合模式具有更高的陀螺常值漂移估計精度。這是由于傳統(tǒng)慣性/天文組合模式在將天文信息進行坐標(biāo)轉(zhuǎn)換時引入了慣性導(dǎo)航位置誤差，隨著慣性導(dǎo)航位置的發(fā)散，使得高精度的天文信息受損，天文量測信息對陀螺常值漂移的估計效果隨著時間的增長逐步減弱。當(dāng)慣性導(dǎo)航位置誤差較大時，天文精度會大大降低，且由于這種天文信息精度變化導(dǎo)致量測噪聲難以設(shè)置，會進一步降低濾波精度。相比于傳統(tǒng)慣性/天文在地理系下進行姿態(tài)組合，對偶四元數(shù)慣性/天文實際采用了慣性系姿態(tài)組合模式，直接有效地使用高精度天文姿態(tài)量測信息，獲得了較高的陀螺漂移估計和慣性系姿態(tài)誤差估計精度。雖然在最終獲取地理系姿態(tài)的過程中，仍然需要使用慣性導(dǎo)航位置，但是由于準(zhǔn)確地對陀螺漂移進行了估計并有效修正陀螺輸出，因此可以明顯地提高組合精度。

3.2.2 方法應(yīng)用性驗證

1)空天飛行器航跡設(shè)計

考慮到慣性/衛(wèi)星/天文組合導(dǎo)航的使用環(huán)境，為了進一步證明算法的應(yīng)用性，本文以空天飛行器為載體對象，利用在軌段飛行航跡進行仿真測試，具體航跡參數(shù)設(shè)置如表6所示，軌道航跡如圖7所示。

表6 空天飛行器在軌段航跡設(shè)置

2)應(yīng)用性仿真驗證

按照3.1節(jié)中的仿真設(shè)置條件進行仿真測試，得到基于對偶四元數(shù)的慣性/衛(wèi)星/天文導(dǎo)航誤差統(tǒng)計值，如表7所示。在衛(wèi)星失效情況下，慣性/天文導(dǎo)航誤差如表8所示。

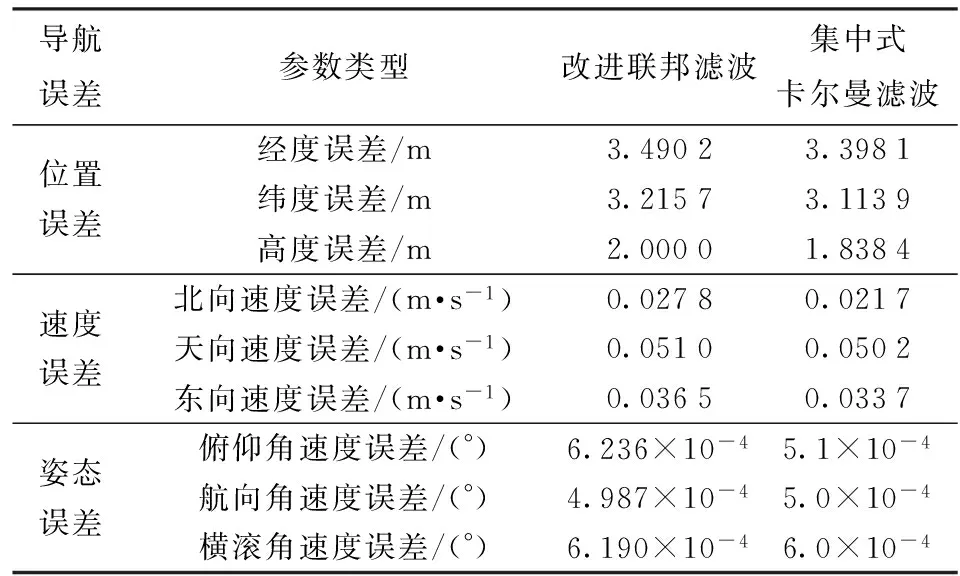
表7 基于對偶四元數(shù)的慣性/衛(wèi)星/天文導(dǎo)航誤差均方根值統(tǒng)計(應(yīng)用性驗證)

對比表7中的誤差統(tǒng)計數(shù)據(jù)可知，空天飛行器在軌飛行運動過程中，基于對偶四元數(shù)的改進聯(lián)邦濾波方法與集中式卡爾曼濾波具有基本一致的精度。通過表8可知，在衛(wèi)星失效的情況下，基于對偶四元數(shù)的降維慣性/天文組合相比于傳統(tǒng)慣性/天文組合具有更高的姿態(tài)、速度、位置(三維矢量和)精度。

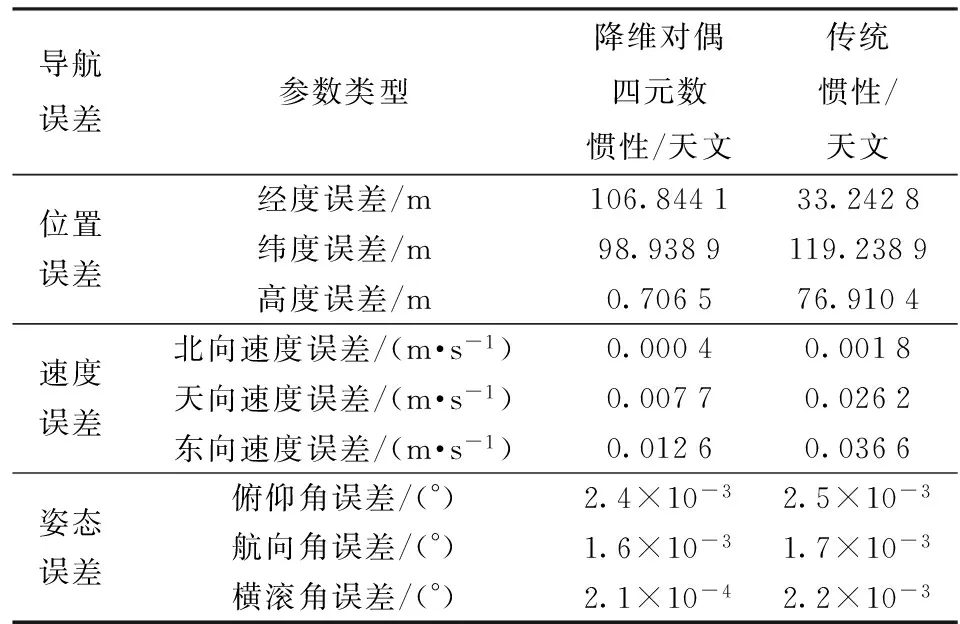
表8 慣性/天文導(dǎo)航誤差均方根值統(tǒng)計(應(yīng)用性驗證)

綜上所述，本文所提出的基于對偶四元數(shù)的慣性/衛(wèi)星/天文改進聯(lián)邦濾波算法可以在保證導(dǎo)航精度的同時減少計算量，且能在衛(wèi)星故障或信號丟失的情況下獲得相較于傳統(tǒng)慣性/天文更高的導(dǎo)航精度。

4 結(jié)論

傳統(tǒng)地理系下慣性/衛(wèi)星/天文組合導(dǎo)航系統(tǒng)聯(lián)邦濾波中主濾波和子濾波器中均保留所有狀態(tài)量，而實際天文信息對部分狀態(tài)量不具有可觀測性。傳統(tǒng)慣性/天文在組合前需先將天文姿態(tài)信息轉(zhuǎn)化為地理系姿態(tài)，由于估計回路中引入慣性導(dǎo)航位置誤差，因此狀態(tài)量估計精度逐步降低。針對上述問題，本文提出基于對偶四元數(shù)的慣性/衛(wèi)星/天文改進聯(lián)邦濾波方法，根據(jù)狀態(tài)量的可觀測性建立子濾波器模型，降低子濾波器維數(shù)。基于對偶四元數(shù)的慣性/天文組合模式采用慣性系姿態(tài)組合的方法，直接利用天文信息對陀螺誤差和慣性系姿態(tài)誤差進行準(zhǔn)確估計，相比于傳統(tǒng)慣性/天文組合模式具有更好的導(dǎo)航性能。仿真結(jié)果表明，本文所提出的方法能在減少聯(lián)邦濾波計算量的同時獲得與集中濾波相當(dāng)?shù)木龋l(wèi)星信號丟失情況下相比于傳統(tǒng)慣性/天文組合精度更高，從而為慣性/衛(wèi)星/天文組合模式提供了一種新的有效方法，具有較高的工程應(yīng)用參考價值。

)

[1] Yang Y Q, Zhang C X, Lu J Z. Local observability analysis of star sensor installation errors in a SINS/CNS integration system for near-earth flight vehicles [J]. Sensors, 2017, 17(1):167.

[2] Deng H, LIU G B, Ehen Hao M, et al. The application of federated Kalman filtering in SINS/GPS/CNS integrated navigation system[J]. International Journal of Wireless and Microwave Technologies, 2012, 2(2): 12-19.

[3] 全偉, 劉百奇, 宮曉琳，等. 慣性/天文/衛(wèi)星組合導(dǎo)航技術(shù)[M]. 北京：國防工業(yè)出版社, 2011:6-7.

QUAN Wei, LIU Bai-qi, GONG Xiao-lin, et al. INS/CNS/GNSS integrated navigation technology[M]. Beijing: National Defense Industry Press, 2011:6-7. (in Chinese)

[4] 張科, 劉海鵬, 李恒年,等. SINS/GPS/CNS 組合導(dǎo)航聯(lián)邦濾波算法[J]. 中國慣性技術(shù)學(xué)報, 2013, 21(2):226-230.

ZHANG Ke, LIU Hai-peng,LI Heng-nian,et al. SINS/GPS/CNS integrated navigation federal filtering algorithm[J]. Journal of Chinese Inertial Technology, 2013, 21(2):226-230. (in Chinese)

[5] 趙慧, 熊智, 施麗娟,等. 基于慣性系下陀螺誤差在線估計修正的慣性與星光組合導(dǎo)航方法[J]. 兵工學(xué)報, 2016, 37(12):2259-2267.

ZHAO Hui, XIONG Zhi, SHI Li-juan, et al. A SINS/STAR integrated navigation method based on online estimation of gyroscope error in inertial coordinate[J]. Acta Armamentarii, 2016, 37(12):2259-2267. (in Chinese)

[6] 錢華明, 孫龍, 黃蔚, 等. 基于加性對偶四元數(shù)的慣性/天文組合導(dǎo)航算法[J]. 北京航空航天大學(xué)學(xué)報, 2013, 39(6): 739-744.

QIAN Hua-ming, SUN Long,HUANG Wei,et al. SINS/CNS integrated navigation algorithms based on dual quaternion[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(6): 739-744. (in Chinese)

[7] 武元新. 對偶四元數(shù)導(dǎo)航算法與非線性高斯濾波研究[D]. 長沙：國防科學(xué)技術(shù)大學(xué), 2005:24-35.

WU Yuan-xin. Research on dual-quaternion navigation algorithm and nonlinear Gaussian filtering[D].Changsha: National University of Defense Technology, 2005:24-35. (in Chinese)

[8] Wang R Y, Liu W C, Bian H W, et al. Fast alignment algorithm with order-reduced filter for SINS[J]. Journal of Chinese Inertial Technology, 2016, 24(5):607-618.

[9] 朱蘭偉, 張燕, 蔡春龍. 基于可觀測性分析的光纖陀螺SINS/測速儀組合系統(tǒng)技術(shù)[J]. 中國慣性技術(shù)學(xué)報, 2011, 19(1):50-54.

ZHU Lan-wei, ZHANG Yan, CAI Chun-long. FOG SINS/speedometer integrated system technique based on observability analysis[J]. Journal of Chinese Inertial Technology, 2011, 19(1):50-54. (in Chinese)

[10] 衣曉, 何友, 關(guān)欣. 基于不同局部模型的聯(lián)合濾波算法研究[J]. 中國慣性技術(shù)學(xué)報, 2002, 10(5):16-19.

YI Xiao, HE You, GUAN Xin. Federated filtering algorithm based on different local models[J]. Journal of Chinese Inertial Technology, 2002, 10(5):16-19. (in Chinese)

[11] Gu Q T, Fang J. Global optimality for generalized federated filter[J]. Acta Automatica Sinica, 2009, 35(10):1310-1316.