基于非線性規劃的重力壩深層抗滑穩定優化算法研究
李 澤, 劉 毅, 胡 政, 周 宇
(昆明理工大學 建筑工程學院, 云南 昆明 650500)
1 研究背景
重力壩是依靠自重產生的抗滑力來擋水的水工建筑物,是水利水電工程中一種常見的壩型。由于重力壩具有較好的安全性和經濟性,其在水利水電行業得到了廣泛的應用。隨著水電建設的發展和建設規模的日益增大,具有完整基巖的重力壩址越來越少,大部分重力壩均修建在地質條件復雜的巖基上,因此復雜壩基的重力壩抗滑穩定問題變得日益突出[1-6]。諸多學者對重力壩的抗滑穩定分析一直在進行研究,取得了較大的成果[7-11]。其中郭明偉等[12]對混凝土重力壩雙滑面抗力方向角的取值研究取得了較大成果。
重力壩壩基巖體中存在著大量的軟弱結構面時,對壩體抗滑穩定將產生不利影響,當作用在壩體及巖體上的荷載達到一定值時,壩基會沿著一個或多個軟弱結構面組成的復合滑面發生破壞。根據重力壩壩基軟弱結構面產狀的不同,重力壩壩基深層滑動破壞可分為4種類型[13]:單斜剪切滑動破壞、雙斜剪切滑動破壞、尾巖抗力體擠壓破壞和尾巖抗力體隆起破壞。在這4種類型中,最常見的類型為:單斜剪切滑動破壞、雙斜剪切滑動破壞。
單斜剪切滑動破壞屬于單滑面情況,其計算比較簡單,一般參照重力壩沿建基面滑動的抗滑穩定公式進行計算。雙斜滑動穩定性分析較單斜剪切滑動破壞復雜,其計算方法主要有3種:被動抗力法、等安全系數法、剩余推力法。其中等安全系數法為水利行業的重力壩設計規范所采用。等安全系數法的主要思想是:采用抗剪斷強度公式分別核算兩個滑面上的抗滑安全系數,并令這兩個安全系數相等,然后采用迭代法確定安全系數的值[14]。
等安全系數法主要可用于以下兩類深層抗滑穩定的計算:第1類是壩體帶動一塊基巖沿緩傾角并露頭的連續雙滑動面滑動;第2類是壩基緩傾軟弱結構面未露頭,也無可壓縮層,但可能發生部分下游基巖的剪斷而產生滑動。對于第1類情況,可應用等安全系數法直接計算抗滑穩定的安全系數;但對于第2類情況,下游基巖的斷裂面一般難以確定,現階段的設計方法一般是先假定一個下游基巖的斷裂面,再進行抗滑穩定分析,然而此方法并不能夠確定
最不利的下游基巖的斷裂面。
基于上述分析,針對壩基緩傾軟弱結構面未露頭,但可能發生部分下游基巖的剪斷而產生滑動的情況,本文提出了一種重力壩壩基雙斜滑動臨界破壞滑面的計算方法。
2 重力壩壩基深層抗滑穩定計算
當壩基深層存在緩傾角結構面,按地質資料可分為3類,分別是單滑動面、雙滑動面和多滑動面,按此3類進行抗滑穩定分析。其中最常見的為雙滑動面,圖1為雙滑面典型示意圖。
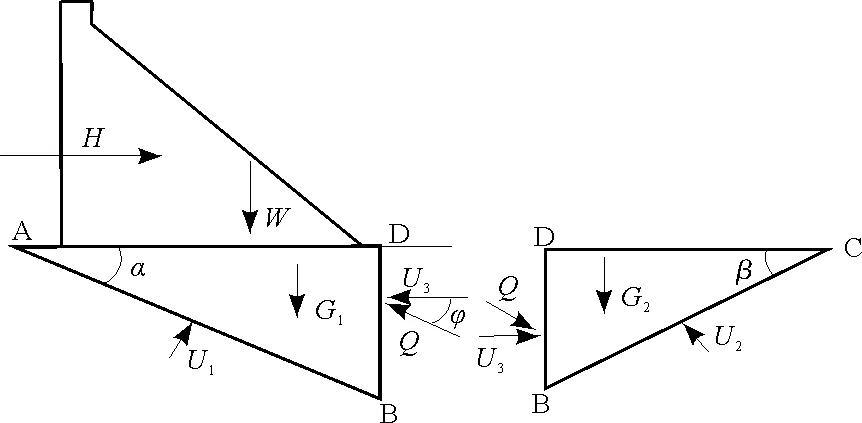
圖1 重力壩壩基雙滑動面典型示意圖
采用等安全系數法計算深層抗滑穩定,可按抗剪斷強度公式或抗剪強度公式進行計算,本文針對圖1所示的雙滑面情況采用抗剪斷強度公式進行計算[14]。
考慮ABD塊的穩定,則有:
(1)
考慮BCD塊的穩定,則有:
(2)
3 基于非線性規劃的重力壩深層抗滑穩定的優化算法模型
3.1 重力壩壩基深層抗滑穩定計算的相關參數
重力壩壩基緩傾軟弱結構面未露頭,部分下游基巖發生剪斷而產生滑動的雙斜滑動受力圖如圖1所示。圖1中:ADC為重力壩建基面,AB為緩傾軟弱結構面,BC為下游基巖發生剪斷的破壞滑面,BD為滑塊ABD、BCD的分界面。根據重力壩的實際情況,可確定其計算參數,主要包括:重力壩壩體、基巖幾何參數、材料參數(包括壩體、基巖和軟弱結構面的容重、凝聚力、摩擦角)、荷載參數。
3.2 非線性數學規劃模型
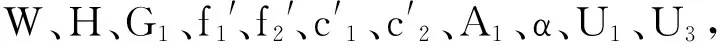
(3)
3.2.2 目標函數 對于重力壩深層抗滑穩定問題,一般定義安全系數為:K′=抗滑力/滑動力。本文將重力壩抗滑穩定安全系數K′作為目標函數,并尋求其對應于下游基巖巖體臨界破壞滑面BC的最小值。
3.2.3 等安全系數法約束方程 根據重力壩深層抗滑穩定計算的等安全系數法,圖1所示的重力壩在發生雙斜面滑動時,根據式(1)、(2),ABD、BCD滑塊應滿足以下約束方程:
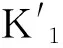
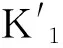
(4)
3.3 求解重力壩壩基雙斜滑動臨界破壞滑面的非線性數學規劃模型
求解重力壩壩基雙斜滑動臨界破壞滑面的非線性數學規劃模型的目標函數為安全系數,約束條件為等安全系數法方程。數學模型具體表達式為:
(5)
4 非線性規劃
目前對于非線性規劃模型的求解,本文采用序列二次規劃算法(SequentialQuadraticProgrammingMethod)[15]求解本文的非線性數學規劃模型,計算結果包括下游基巖發生剪斷的臨界破壞滑面及其對應的抗滑穩定安全系數。本文的程序框圖如圖2。
5 算例分析
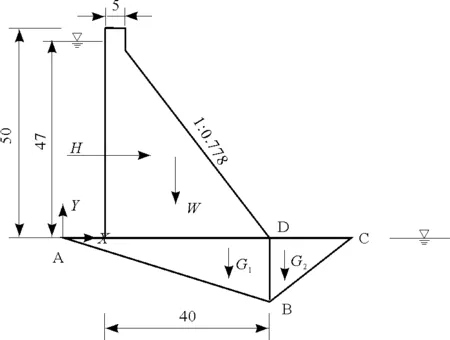
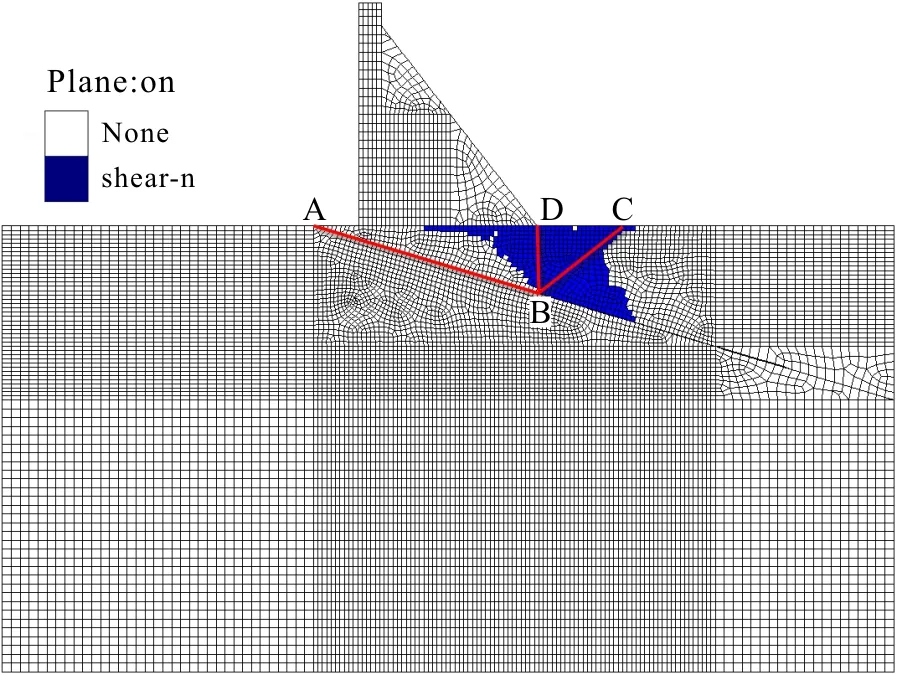
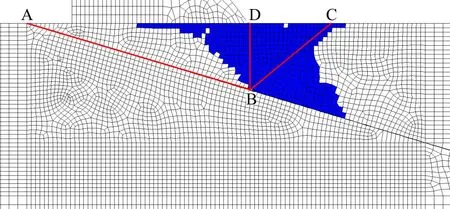
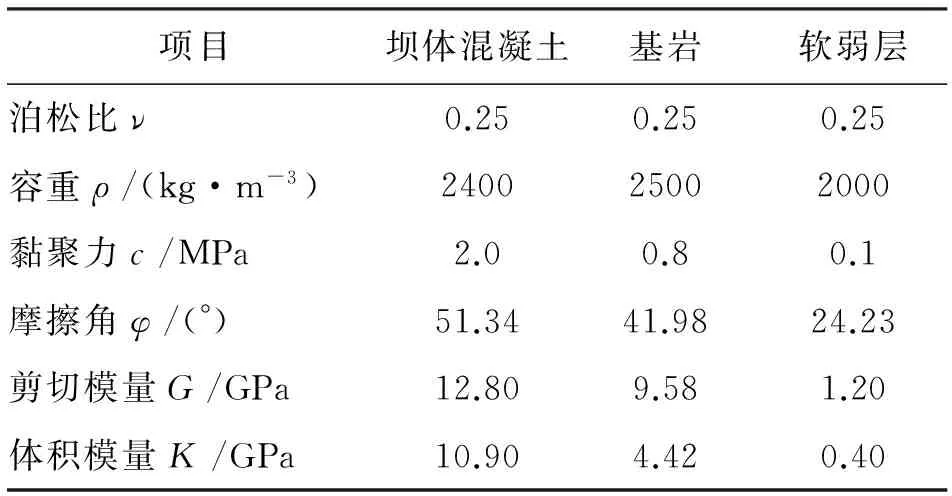
如圖3所示的重力壩,壩高為50.0m,壩頂寬度5.0m,壩底寬度為40m,下游面坡度為1∶0.778,上游正常蓄水位為47.0m,下游水位為0.0m。ADC為建基面,AB為一緩傾軟弱結構面,其傾角為16.7°,BC為下游基巖發生剪斷的滑裂面。A、B、D3點的坐標分別為:A(0, 0)、B(50, -15)、D(50, 0),C點坐標(xC,yC)為決策變量。由于建基面為水平面且C點必須位于D點右側,因此取yC=0,50 圖2 程序框圖 根據以上參數并結合圖1、圖3,進行重力壩抗滑穩定計算的受力分析;并結合數學模型的目標函數、約束條件,可形成求解重力壩下游巖體剪斷破壞臨界滑裂面及其對應的安全系數的非線性數學規劃模型如下。 采用序列二次規劃法求解上述非線性數學規劃模型,計算結果為:下游基巖發生剪斷破壞的臨界滑面C點的坐標為(0.0,76.74645),臨界滑面BC滑面的傾角β,臨界滑面BC的長度為30.6655m,對應于臨界滑面BC的重力壩深層抗滑穩定安全系數K=3.97,巖塊ABD與巖塊BCD之間的作用力Q =15 415 120N。 圖3 重力壩算例示意圖 (單位m) (6) 為了更好地驗算本文所提方法的正確性,本文采用有限元差分法對重力壩進行三維非線性數值模擬分析。根據工程經驗,本文三維數值模型計算深度按照重力壩高度的2倍取值;計算寬度取為重力壩上、下游面到模型邊界1.5~2.0倍的重力壩高度,模型劃分共有32 964個節點,21 716個六面體單元,緩傾軟弱結構面厚度取0.2m(三維數值模型如圖4所示)。重力壩、基巖和軟弱層采用實體單元中的六面體單元進模擬,重力壩模型的計算荷載按現行規范取值[14];模型壩體及基巖的物理力學參數如表1所示。 為了與本文所提方法的計算結果進行比較,在運用有限差分法進行三維非線性數值模擬計算時采用降強法求解基巖屈服破壞時的強度儲備系數,即在計算迭代過程中同時降低材料的黏聚力c和摩擦角φ,直到基巖屈服區貫通失去承載能力為止。強度儲備系數的計算結果是4.0,即將基巖和軟弱層的黏聚力c和摩擦角φ降低4倍的條件下屈服區分布如圖4所示,圖5為基巖屈服區局部放大示意圖,表2為本文方法和有限差分法計算得到的安全系數統計表。 圖4 強度儲備系數為4.0的重力壩塑性區分布示意圖 在圖4、5中深色區域為基巖和軟弱層的屈服區,AB為已知的軟弱層位置,BC為本文所提方法計算得到的臨界滑裂面位置。 圖5 強度儲備系數為4.0的重力壩塑性區分布放大示意圖 項目壩體混凝土基巖軟弱層泊松比ν0.250.250.25容重ρ/(kg·m-3)240025002000黏聚力c/MPa2.00.80.1摩擦角φ/(°)51.3441.9824.23剪切模量G/GPa12.809.581.20體積模量K/GPa10.904.420.40 表2 兩種方法計算結果統計表 由圖可知,基巖屈服區的位置位于重力壩壩趾下部基巖至軟弱層區域,且在強度儲備系數取4.0的條件下由有限差分法得到的屈服區正好沿著BC線貫穿。另外,本文所提方法計算的安全系數為3.97,有限差分法的為4.00,兩種方法計算得到安全系數非常接近。有限差分法計算的結果驗證了本文方法的正確性。 現行重力壩規范對于重力壩深層抗滑穩定分析規定采用的等安全系數法一般只適用于滑面已知的情況,對于壩基緩傾軟弱結構面未露頭,但可能發生部分下游基巖的剪斷而產生滑動的情況,下游基巖的斷裂面一般難以采用等安全系數法確定。故提出了一種將下游基巖發生剪斷破壞滑面的位置變量作為優化變量,以重力壩深層抗滑穩定安全系數作為目標函數,同時以等安全系數法方程作為約束條件,建立重力壩深層抗滑穩定性分析的非線性數學規劃 模型。 本文采用優化方法求解下游基巖發生剪斷的最不利臨界破壞滑面及其對應的最小安全系數。通過算例分析,對比了本文方法與有限差分法所得安全系數的大小,可知該方法概念明確、計算精度高、工程應用簡便,可將其應用于重力壩深層抗滑穩定的分析。在今后的研究中,需在本文工作基礎上對不同類型的滑動破壞模式進行分析研究。 [1] 潘家錚. 建筑物的抗滑穩定和滑坡分析[M].北京:水利出版社, 1980. [2] 陳祖煜,陳立宏. 對重力壩設計規范中雙斜面抗滑穩定分析公式的討論意見[J]. 水力發電學報,2002,21(2):101-108. [3] 黃照賓. 論重力壩深層抗滑穩定問題[J]. 城市建設理論研究:電子版,2013(29). [4] 鄭穎人,趙尚毅. 邊(滑)坡工程設計中安全系數的討論[J]. 巖石力學與工程學報,2006,25(9):1937-1940. [5] 毛巨省. 三峽左廠3號壩段壩基深層抗滑穩定性有限元分析[J]. 西安科技大學學報,2006,26(3):296-299. [6] 周 偉,常曉林,袁林娟. 對重力壩設計規范中雙斜面抗滑穩定的補充討論[J]. 水力發電學報,2005,24(2):95-99. [7] 蔣春艷,常曉林,周 偉. 用于重力壩抗滑穩定分析的分項系數有限元方法[J]. 水力發電學報,2006,25(2):16-20.[8] 于 沭,段慶偉,徐能雄. 龍口水利樞紐廠房壩段深層抗滑穩定分析[J]. 資源與產業,2007,9(3):119-121. [9] 王義鋒,章 青. 基于界面元法的向家壩重力壩深層抗滑穩定分析[J]. 巖土力學,2009,30(9):2691-2696. [10] 馬 剛,常曉林,周 偉,等. 基于Cosserat理論的重力壩深層抗滑穩定分析[J]. 巖土力學,2012,33(5):229-236. [11]SUHuaizhi,HUJiang,LIJinyou,etal.Deepstabilityevaluationofhigh-gravitydamundercombiningactionofpowerhouseanddam[J].InternationalJournalofGeomechanics,2013,13(3):257-272. [12] 郭明偉,王水林,鄧 琴,等. 混凝土重力壩雙滑面抗力方向角的取值研究[J]. 巖土力學,2012,33(6):1864-1868. [13] 郭利娜,李同春,趙蘭浩,等. 重力壩深層抗滑穩定分析[J]. 人民黃河,2011,33(1):101-102105. [14] 中華人民共和國水利部.SL319-2005 混凝土重力壩設計規范[S]. 北京:中國水利水電出版社,2005. [15] 楊慶之. 最優化方法[M]. 北京:科學出版社,2015.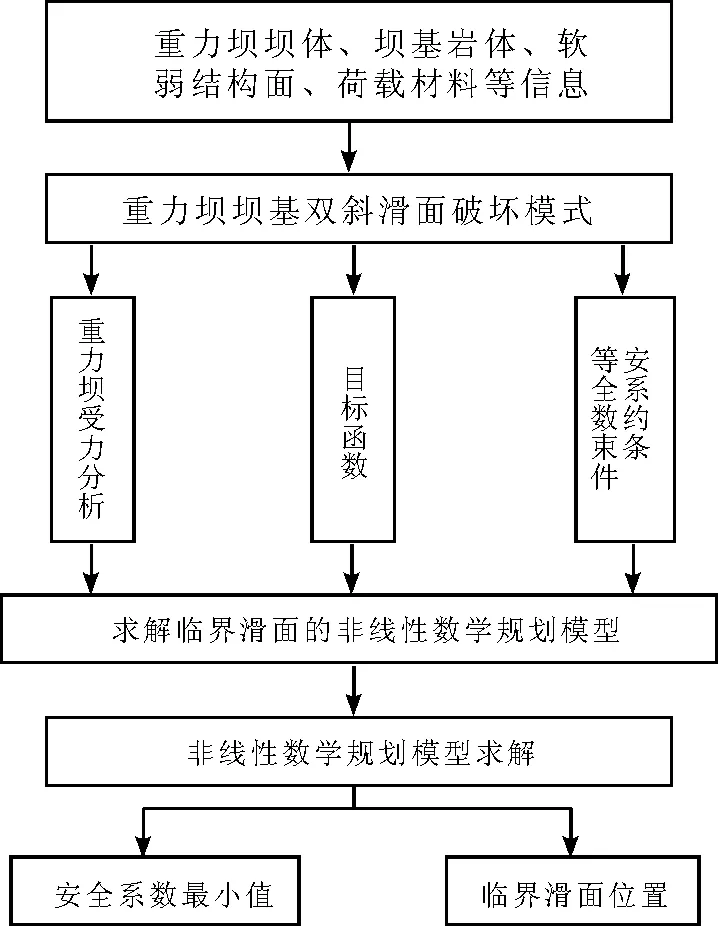
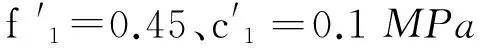

6 結 論

