基于ACO的多序列間最長公共子序列查詢
王虹勝
(四川大學視覺合成圖形圖像技術國防重點學科實驗室,成都 610065)
0 引言
多序列間的最長公共子序列(LCS)查詢廣泛地應用于計算生物學、模式識別、文本比較和數據壓縮等。多序列間的最長公共子序列可以用來度量一組基因序列間的相似度,被廣泛應用于基因測序和蛋白質功能測序等領域。本文主要針對任意數量的生物數據查找最長公共子序列。
經典的雙序列間LCS查詢算法是基于動態規劃(Dynamic Programming)的思想,可以精確查詢出雙序列間的所有最長公共子序列。但是,對于長度為M的N條序列,動態規劃算法的時間復雜度和空間復雜度均為O(MN),隨著數據規模的增大,其復雜度將以指數形式增加,這不利于多序列(N>10)或較長序列(M=500)的查詢。為了進一步提升LCS問題的解決速度,人們提出了近似方法(Approximate Algorithm)和啟發式方法(Heuristic Algorithm)。這兩種方法均以降低求解精度為代價,獲得計算效率的大幅提升。近似方法是指在較短時間內計算出最長公共子序列的近似最優解。最早的LCS近似算法是Long Run方法,該方法在實際應用中的利用率不高。2004年Huang等人提出的 BNMAS(Beat Next for Maximal Available Symbols)算法,但其時間復雜度嚴重依賴于序列集合的字符種類總數。啟發式方法是專為解決NP問題而提出的算法框架,常用于解決多序列間LCS查詢等無法在多項式時間內獲得精確解的問題。2006年Hinkemeyer和Julstrom等人提出了基于遺傳算法(Genetic Algorithm)的LCS查詢算法。2008年Chiang等人對已有的GALCS算法做出部分改進,進一步降低了算法復雜度,該算法查詢質量結果遠高于Long Run算法。
針對現有算法的不足,本文主要利用啟發式算法中的蟻群優化算法(ACO)求解LCS問題,ACO-LCS在查詢效率和結果近似度兩方面均高于GA-LCS算法;并對其中的啟發式因子計算部分做了改進,進一步提高算法的查詢結果質量。
1 最長公共子序列問題模型
在計算機中,生物序列可表示為字符矩陣S={S0,S1,….,Sn-1},矩陣每一行表示一條生物序列Si,且對于任意i(0 ≤i≤1)均有 |Si|=1。Si[j]表示序列Si中下標為j的字符。子序列為一個嚴格遞增的下標數組對應的字符序列。例如,對于序列Si=CTATGA,下表數組p=[0 ,2,4,5]對應的子序列為CAGA。同理,N條序列間的長度為D的任意公共子序列S,可以表示為一個D×N的下標矩陣CS,即CS[i][j]表示S的第i個字符在原始序列Sj中的下標。不同的公共子序列具有不同的下標矩陣,因此,下標矩陣可以作為公共子序列的唯一標識。下標矩陣CS具有如下兩個特點:
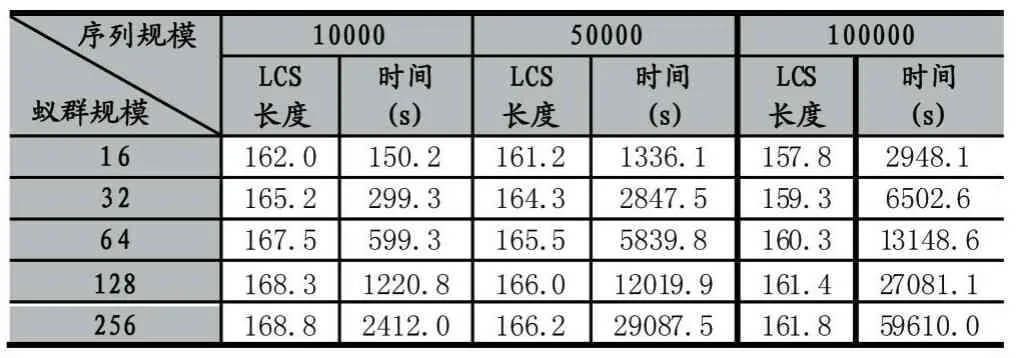
(1)對于給定的行號i,CS[i][j]和CS[i][k]對應的字符相同,其中0≤i (2)下標矩陣每列存儲的下標值嚴格遞增。即CS[i][j] 對 于 給 定 的 序 列 集 合 S={S0:ATCACG,S1:TTCTAG,S2:TCCAGA},其長度為 4的公共子序列s=TCAG可由一個4×3的下標矩陣表示。該矩陣存儲了公共子序列s中的四個字符在所有原始序列中的下標。例如,矩陣的第0行[1 0 0]表示s的第0個字符T在原始序列S0中的下標為1,在原始序列S1和S2中的下標為0。矩陣的第0列則表示公共子序列s中的四個字符分別對應原始序列 S0中的下標為 1、2、3、5 的字符。 當下標矩陣CS的行數D達到最大值時,即為最長公共子序列的字符下標矩陣,遍歷矩陣的任意一列即可計算出序列集合的最長公共子序列。因此,LCS問題可以轉換為計算最大行數的字符下標矩陣的問題。在本文中,我們將利用蟻群優化算法來解決該問題。 (3)蟻群優化算法在LCS問題中的應用 對于給定的序列矩陣S={S0,S1,….,Sn-1},其最長公共子序列是所有原始序列的子序列,因此通過遍歷任意一條原始序列均可得出序列間的LCS下標矩陣。蟻群優化算法模擬了一個規模為M的人工蟻群A={A0,A1,…,AM-1},每只螞蟻Ai隨機地分配一條序列Sj,以遍歷該序列為基準來查詢序列間的最長公共子序列。 螞蟻Ai把原始序列Sj看作自然環境中的地面,把序列中每個字符s及其下標p組成的組對(s ,p)視作地面上的一個位置點。所有滿足下標矩陣特點的未訪問位置點為Ai的可轉向位置點,即若s為所有原始序列的公共字符,且s在每條原始序列中的下標p大于該序列已被訪問位置點的下標值,則(s ,p)為可轉向位置點。螞蟻Ai模擬自然界中蟻群覓食時的尋路方式,評估所有位置點的可轉向性,若(s ,p)滿足下標矩陣的特點,即將字符s在所有原始序列中的下標作為新的一行加入螞蟻Ai構建的LCS下標矩陣中。螞蟻Ai以(s ,p)作為當前位置繼續向前訪問,不斷地將滿足下標矩陣特點的位置點對應的下標添加進LCS下標矩陣中,直到遍歷完序列Sj的最后一個位置點,便可得到該螞蟻構建的近似LCS下標矩陣。圖1為螞蟻Ai的一次構建過程。 圖1 LCS下標矩陣構建過程 初 始 時 下 標 矩 陣 為 空 ,位 置 點(A ,0),(T ,1),(C ,2),(A ,4)均為可轉向位置點。假設Ai選擇轉向位置點(A ,0),則搜索(A ,0)在所有原始序列中的下標[0 ,3,1],并將其作為第0行加入下標矩陣中。Ai繼續評估下一個位置點(T ,1),分別以3和1為當前下標在原始序列S1和S2中搜索字符T,未搜尋到則表示(T ,1)不是當前的可轉向點。Ai繼續以[0 ,3,1]為當前下標評估下一個位置點(C ,2),并將其對應的下標數組[2 ,4,2]作為新的一行加入LCS下標矩陣中。直到S0遍歷結束螞蟻便可構建出路徑(A ,0)→(C ,2)對應的行數為2的下標矩陣,其對應的公共子序列為AC。然而,若要構建出行數較大的下標矩陣,還需要螞蟻有效地選擇“較好”的可轉向點。 螞蟻在遍歷原始序列時,所有滿足下標矩陣要求的未訪問位置點均為其候選轉向的位置點,螞蟻通過評估轉向每個位置點可獲得更長公共子序列的可能性,來選擇出“較好”的位置點。在圖1中,若螞蟻首次選擇時放棄位置點(A ,0),選擇轉向位置點(T ,1),則可構建出路徑(T ,1)→(C ,2)→(A ,4)對應的行數為3的下標矩陣,其對應的公共子序列TCA。因此,字符T是比A更好的候選轉向。在實際LCS問題中,螞蟻通常無法直觀地判斷那個字符“較好”,只能通過位置點(s ,p)的特性計算其能獲取更長公共子序列的可能性來覺得是否選擇。這種可能性被稱作字符的轉換概率。轉換概率的決定因素主要是位置點(s ,p)的信息素因子和啟發式因子。 位置點(s ,p)的信息素因子實現了蟻群系統的正反饋性,使每只螞蟻有了經驗學習的能力,從而有效地選擇“較好”字符。螞蟻每次選擇一個位置點(s ,p)后,便會在改點及其在所有原始序列中的對應位置點上排放一定量的信息素。隨著蟻群不斷地選擇。位置點(s ,p)上信息素的積累量,表示為τ(s,p)。τ(s,p)越大表示該字符在蟻群歷史構建過程中被選擇的次數越多,是“較好”字符的可能性也就越大。位置點(s ,p)的啟發式因子是指局部范圍內,轉向位置點(s ,p)可獲得更長公共子序列的可能性,表示為η(s,p)。η(s,p)值反映了每只螞蟻的局部搜索能力。信息素因子和啟發式因子共同決定了螞蟻構建LCS過程中的每次字符選擇。啟發式因子具體計算公式如式(1)所示: 蟻群系統的交流和優化主要由信息素機制實現。螞蟻通過每個位置點的信息素累積量,獲取整個蟻群對于該位置點的歷史選擇經驗,從而實現蟻群系統的學習和協作。每輪構建結束后,蟻群優化算法會在所有螞蟻構建的LCS下標矩陣中,選出行數最大的一個作為本輪迭代的最優解。同時維護一個歷史最優解,若當前輪產生的本輪最優解行數大于當前歷史最優解,則更新歷史最優解。在LCS問題中,信息素表示為一個與序列矩陣S同等規模的矩陣τ[N][D],τ[N][D]存儲了字符Si[j]位置的信息素累積量。蟻群在每輪構建LCS下標矩陣完成之后便會對全局信息素矩陣進行更新操作,以反饋蟻群的當前構建情況,為下一輪構建提供經驗學習。信息素的更新主要包括信息素隨時間揮發的減少量,以及優質的LCS下標矩陣儲存位置點的排放量。信息素更新公式如(2)所示,其中ρ為每輪構建過程中信息素的揮發率。Δτ[i][j]為本輪構建過程中Si[j]位置信息素的總排放量。φ為信息素排放系數,且φ∈(0,1),以防信息素排放量過高,使得某條路徑信息素積累量明顯高于其他路徑,造成蟻群系統過早停滯。 蟻群優化算法是一個群體智能算法,群體的規模對算法構建的質量和效率都有一定影響。蟻群優化算法中螞蟻數量越多時,構建的公共子序列種類也就越多,可查詢到更長的公共子序列的可能性也就越大。但是,當構建的公共子序列種類數過多時,大部分位置點的信息素便會趨于平均,這極大地抑制了蟻群系統的正反饋性,導致算法收斂速度變慢,影響最長公共子序列的查詢效率。而若蟻群規模太小,算法很容易出現停止現象,不利于最優解的構建。本實驗以不同規模的DNA序列集合為例,研究不同蟻群規模對算法查詢效率和查詢結果長度的結果。如表1所示,隨著蟻群規模不斷增大,算法查詢的公共子序列長度隨之變化,并且查詢時間消耗成倍增加,但螞蟻構建出的下標矩陣多樣性增加,查詢到的公共子序列長度也逐漸增加。但當蟻群規模增加到一定程度時,其查詢出的公共子序列長度增加量逐漸減小,查詢長度提升逐漸變得不明顯。 表1 蟻群規模對LCS查詢性能影響 本文分析了蟻群優化算法查詢最長公共子序列的基本思想和大致流程,采用基于蟻群優化算法實現了多序列間的最長公共子序列查詢。本文通過大量的實驗研究并分析了不同蟻群規模對查詢算法的性能影響,確保蟻群優化算法可有效解決LCS問題。 [1]Dorigo M,Birattari M,Stutzle T.Ant colony optimization[J].IEEE Computational Intelligence Magazine,2006,1(4):28-39. [2]Bullnheimer B,Hartl R,Strauss C.A New Rank Based Version of the Ant System.A Computational Study[J].1997,7(1):25-38. [3]Stutzle T,Hoos H.MAX-MIN Ant System[J].Future Generation Computer Systems,2000,16(8):889-914. [4]Dorigo M,Maniezzo V,Colorni A.Positive Feedback as a Search Strategy[J].,1991.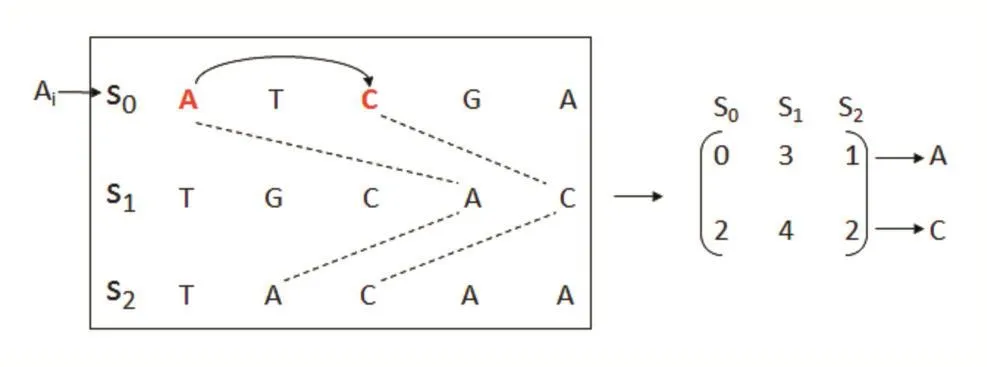
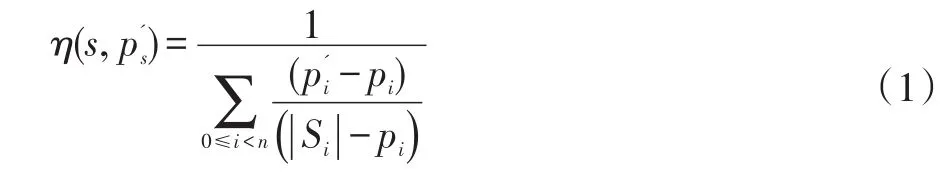
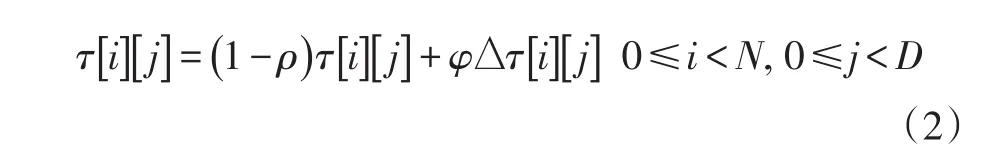
2 實驗結果分析
3 結語

