海量數據的支持向量機優化挖掘方法

李清霞

摘 要： 傳統支持向量機挖掘方法可以對領域數據實現挖掘，但在復雜多變環境下數據挖掘離散程度較大。提出海量數據的支持向量機優化挖掘方法，構造靜態粒子空間，局限海量數據挖掘離散程度，形成小規模的、多簇團的粒子挖掘數據集；將單粒子挖掘數據進行離散性擬合，以多簇團粒子整合離散運算，保證挖掘計算進行周期性運行；對同軌挖掘計算進行條件約束，實現小離散程度的數據挖掘。仿真實驗驗證結果表明，支持向量機優化挖掘方法在復雜多變環境下具有較高的穩定性，并且挖掘離散度小、挖掘信息精度較高。

關鍵詞： 海量數據； 支持向量機； 多簇團粒子； 數據擬合； 整合運算； 挖掘離散； 優化方法

中圖分類號： TN911?34； TN913 文獻標識碼： A 文章編號： 1004?373X（2018）06?0137?04

Abstract： The traditional data mining method based on support vector machine （SVM） can mine the domain data， but has high data mining dispersion degree in the complex and changeable environment. Therefore， an SVM?based optimization mining method of massive data is proposed to construct the static particle space， limit the data mining discrete degree， and form the small?sized and multi?cluster particle mining data sets. The discrete fitting is carried out for the single?particle mining data， and the multi?cluster particles are integrated for discrete operation to ensure the periodical operation of mining calculation. The conditional constraint is performed for the one?orbit mining calculation to realize the data mining with low discrete degree. The simulation experimental results show that the optimization mining method based on SVM has high stability in the complex and changeable environment， low mining discrete degree and high information mining accuracy.

Keywords： massive data； support vector machine； multi?cluster particle； data fitting； integration operation； mining dispersion； optimization method

0 引 言

支持向量機是近年來廣泛受到關注的機器學習與分析方法，廣泛應用于函數估計、模式識別、圖像處理和生物信息學等諸多領域。傳統的支持向量機挖掘方法可以對領域內數據進行挖掘，但在復雜多變環境條件下，存在挖掘離散性較高的問題。根據以上問題，提出海量數據的支持向量機優化挖掘方法。實驗結果表明，海量數據的支持向量機優化挖掘方法，在多變復雜的環境下具有良好的穩定性，在較小的離散性下保持較高的數據挖掘精度。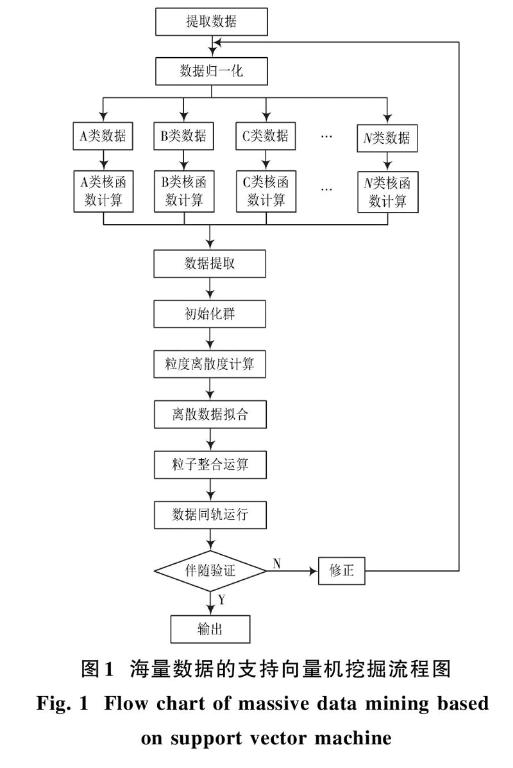

1 海量數據的支持向量機優化挖掘技術

1.1 構建靜態粒子空間局限離散程度

對單個數據單元進行離散性提取，將具有同一性的數據進行歸一化處理，利用核函數的計算，將反應同一性的參數進行粒子運算，海量信息計算提取的同一性數據定義了初始化群的離線性質[1]。對定義后的初始化群粒子進行離散度約束，形成靜態粒子空間。通過靜態粒子空間，刪除失真數據，在空間粒子離散度受到空間的局限。在進行粒子的整合運算時[2]，將粒子數據整合，挖掘數據會按照局限進行同軌運行計算，周期計算存在一定的偏差，運行偏差較大時會加大離散程度，因此需要重新認定挖掘數據[3?4]。偏差度為零或者較小時可將挖掘數據進行輸出。本文設計的海量數據的支持向量機挖掘流程圖如圖1所示。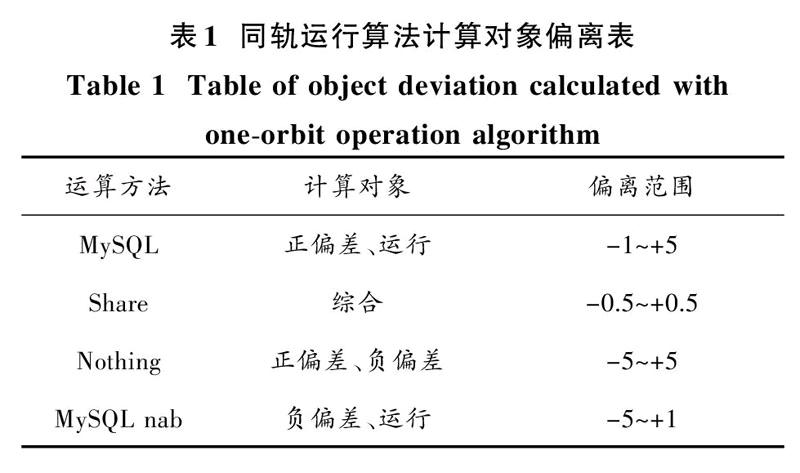

1.2 離散性擬合計算

離散數據擬合計算是根據定義的初始化群粒子的特性，進行離散度的整合計算。將離散度高的數據進行擬合計算，剔除原有數據屬性，成為新的具有合理性粒子的挖掘數據，擬合計算過程用粒子整合離散中的擬合屬性，對數據超過平均浮動的粒子進行剝離[5?6]，對超過5倍浮動的粒子進行規律性的刪除，對平均方差為3～5倍的粒子進行比例擬合整合[7?8]，保證單個粒子的計算精度。其離散數據擬合過程如圖2所示。

粒子通過離散數據擬合計算，形成多簇團粒子空間，對多簇團粒子空間進行粒子整合，粒子模擬整合[9]可分為點動整合和線動整合兩種。其多簇團粒子整合示意圖如圖3所示。endprint

點動整合是大部分多簇團粒子呈線性分布，而在整合曲線上出現單簇團或多處簇團偏離呈現。將偏離整合曲線的簇團進行合理移動，其最大移動值不能超過簇團局限數據，離散數據擬合整合前的最大值是移動的最小值[10]，實現多簇團周期規律運行。線動整合是較多的簇團粒子呈無規律分布，且數據挖掘呈偏離狀態，整合曲線連接多簇團粒子代表性差。因而進行整合曲線的調整[11]，即線動整合。整合曲線的調整必須滿足有[12]的粒子在整合曲線外，且整合曲線上的粒子不能代表所有多簇團粒子的計算值。整合曲線移動原則要盡可能地連接所有多簇團粒子，連接具有代表性以及規律性。對不能連接所有多簇團粒子的，先進行線動整合后，再進行點動整合，使挖掘數據具備周期性。

1.3 實現低離散度數據挖掘

對多簇團粒子整合運算后，進行數據的同軌挖掘運算，海量數據的支持向量機挖掘方法，具有一定的數據代表性，但數據代表性需進行挖掘伴隨性驗證，驗證成功后對挖掘數據進行輸出，其同軌運算選用偏正挖掘數據與負偏挖掘數據，實測挖掘數據能夠進行同軌計算，保證運行正負偏差固定，以保證同軌挖掘運算的穩定性。其數據挖掘同軌框架圖如圖4所示。

通過MySQL，Share，Nothing，MySQL nab計算方法，根據數據挖掘特點，進行不同對象的挖掘計算，伴隨同軌挖掘計算周期運行。其同軌運行算法的離散程度與偏離數據如表1所示。

通過周期挖掘計算的同軌運行，穩定地挖掘數據信息，利用硬件設備進行數據傳遞，對不穩定的挖掘數據、離散較大的數據進行重新粒子擬合、多簇團粒子的整合運算。重新擬定同軌計算，保證對每組挖掘數據的結果不帶有離散性，從而實現海量數據的支持向量機數據挖掘。

2 仿真實驗與測試

為了驗證解決支持向量機的挖掘方法的有效性，本文采用傳統數據挖掘方法與海量數據支持的向量機數據挖掘方法進行對比實驗，利用支持向量機的離散程度測試和斜方差分析驗證支持向量機的挖掘方法的有效性。

通過仿真模擬實驗，對特定實驗對象進行數據挖掘不少于10萬次或2 h。采用兩種支持向量機的挖掘，記錄標記數據點，利用計算機系統生成離散程度分布圖，如圖5所示。

根據離散程度分布圖可以看出，傳統數據挖掘方法的數據挖掘能力的浮點率較高，離散程度較大。并且存在個別失真點，數據不確定性。具有3處挖掘數據集中心域，一次為零偏差范圍，其他兩次分別存在正偏差和負偏差。

方差分析是調節協變量對因變量的影響效應，對實驗進行統計控制的一種綜合方差分析和回歸分析的方法。通過綜合方差分析與回歸分析，得出斜方差分析圖，如圖6所示。

圖6中：[Σx]代表穩定值；[Σy]代表離散值。[Σx]小于2代表穩定，[Σx=0]代表測量值恒定最穩定。[Σy]小于4代表離散現象可以忽略不計，[Σy=0]代表測量值無離散現象。基于斜方差分析圖，對[Σx]與[Σy]進行測定，其傳統數據挖掘方法的穩定性為[Σx=1]、離散性為[Σy=3]，海量數據的支持向量機數據挖掘方法的穩定性為[Σx=0.3]、離散性為[Σy=1]。通過離散程度測試、變異系數測試和斜方差分析實驗的結果。說明海量數據的支持向量機數據挖掘方法具有良好的離散性、數據可靠性。

3 結 語

通過靜態離粒子空間的構建，以及粒子的多重去離散性運算，優化挖掘方法，經實驗驗證結果表明，海量數據的支持向量機優化挖掘方法，在復雜多變的環境下，具有較小的離散性、良好的穩定性以及挖掘精度。

參考文獻

[1] 肖白，聶鵬，穆鋼，等.基于多級聚類分析和支持向量機的空間負荷預測方法[J].電力系統自動化，2015，39（12）：56?61.

XIAO Bai， NIE Peng， MU Gang， et al. A spatial load forecasting method based on multilevel clustering analysis and support vector machine [J]. Automation of electric power systems， 2015， 39（12）： 56?61.

[2] 王寧，謝敏，鄧佳梁，等.基于支持向量機回歸組合模型的中長期降溫負荷預測[J].電力系統保護與控制，2016，44（3）：92?97.

WANG Ning， XIE Min， DENG Jialiang， et al. Mid?long term temperature?lowering load forecasting based on combination of support vector machine and multiple regression [J]. Power system protection and control， 2016， 44（3）： 92?97.

[3] 焦衛東，林樹森.整體改進的基于支持向量機的故障診斷方法[J].儀器儀表學報，2015，36（8）：1861?1870.

JIAO Weidong， LIN Shusen. Overall?improved fault diagnosis approach based on support vector machine [J]. Chinese journal of scientific instrument， 2015， 36（8）： 1861?1870.

[4] 王瑜，苑津莎，尚海昆，等.組合核支持向量機在放電模式識別中的優化策略[J].電工技術學報，2015，30（2）：229?236.

WANG Yu， YUAN Jinsha， SHANG Haikun， et al. Optimization strategy research on combined?kernel support vector machine for partial discharge pattern recognition [J]. Transactions of China electrotechnical society， 2015， 30（2）： 229?236.endprint

[5] 薛浩然，張珂珩，李斌，等.基于布谷鳥算法和支持向量機的變壓器故障診斷[J].電力系統保護與控制，2015，43（8）：8?13.

XUE Haoran， ZHANG Keheng， LI Bin， et al. Fault diagnosis of transformer based on the cuckoo search and support vector machine [J]. Power system protection and control， 2015， 43（8）： 8?13.

[6] 張玉欣，程志峰，徐正平，等.參數尋優支持向量機在基于光聲光譜法的變壓器故障診斷中的應用[J].光譜學與光譜分析，2015，35（1）：10?13.

ZHANG Yuxin， CHENG Zhifeng， XU Zhengping， et al. Application of optimized parameters SVM based on photoacoustic spectroscopy method in fault diagnosis of power transformer [J]. Spectroscopy and spectral analysis， 2015， 35（1）： 10?13.

[7] 李霄，王昕，鄭益慧，等.基于改進最小二乘支持向量機和預測誤差校正的短期風電負荷預測[J].電力系統保護與控制，2015，43（11）：63?69.

LI Xiao， WANG Xin， ZHENG Yihui， et al. Short?term wind load forecasting based on improved LSSVM and error forecasting correction [J]. Power system protection and control， 2015， 43（11）： 63?69.

[8] 梁禮明，鐘震，陳召陽.支持向量機核函數選擇研究與仿真[J].計算機工程與科學，2015，37（6）：1135?1141.

LIANG Liming， ZHONG Zhen， CHEN Zhaoyang. Research and simulation of kernel function selection for support vector machine [J]. Computer engineering and science， 2015， 37（6）： 1135?1141.

[9] SHAO Y H， HUA X Y， LIU L M， et al. Combined outputs framework for twin support vector machines [J]. Applied intelligence， 2015， 43（2）： 424?438.

[10] GUI G， PAN H， LIN Z， et al. Data?driven support vector machine with optimization techniques for structural health monitoring and damage detection [J]. KSCE journal of civil engineering， 2017， 21（2）： 523?534.

[11] THARWAT A， HASSANIEN A E， ELNAGHI B E. A BA?based algorithm for parameter optimization of support vector machine [J]. Pattern recognition letters， 2017， 93（7）： 13?22.endprint