一種改進的小波尺度相關閾值去噪方法*

袁偉家，劉雨東，翟春平

0 引 言

聲波在水中具有比電磁波更遠的傳播距離，使得水聲信號應用范圍廣泛。聲信號通過聲吶（換能器）發出，以實現水下目標識別，如水雷探測定位、目標跟蹤以及通訊等功能。由于海洋信道復雜多變，海洋背景噪聲和信號在采集、傳輸、接收甚至傳輸中的電路震蕩，都會不可避免地引入噪聲，使得接收聲信號產生畸變和失真，因此信號具有非平穩特性[1]。噪聲的出現影響了信號的接收和后續處理，因此必須對噪聲加以抑制。傳統的去噪方法有低通濾波去噪、FFT去噪[2]等。FFT去噪不能實現時域細分，且難以檢測到局域突變信號，導致去噪的同時部分有用信號的信息也會損失。傳統去噪算法通常不能將處于同頻帶的信號和噪聲區分開，而小波分解能夠克服這一局限[3]。在小波去噪領域，Donoho[4]提出的閾值去噪法得到了實際應用，但硬閾值函數在λ處不連續，導致小波分解系數重構時出現偽吉布斯（Pseudo-Gibbs）效應，從而使信號失真、震蕩或圖像信號模糊。而軟閾值函數一階可導整體具有較好的連續性，但存在固定的偏差。劉娟花[5]等人比較了小波基和閾值選取規則，提出了一種改進的去噪算法，取得了一定效果。為達到更高的信噪比，降低有用信號的信息損失，很多學者將注意力集中到小波系數的相關性上，如小波尺度內相關算法[3]和尺度間相關算法[6-7]利用信號與噪聲在不同尺度模型的相關性去噪，提升了算法性能，但也增加了巨大的計算量。

針對上述缺陷，本文在小波變換基礎上提出了一種改進的小波尺度相關閾值去噪法。采用空域相關算法能夠保留信號突變處的信息[8]，捕捉水聲信號多尖峰的特征，同時采用小波變換克服信號非平穩的特性。

1 算法原理

1.1 二進制離散小波變換

連續小波函數[9]的一般形式為：

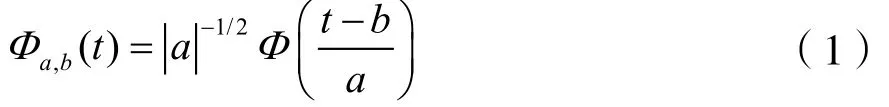
式中，b∈R，a∈R+，且a≠0，Φa,b(t)滿足容許性條件[10]。為簡便起見，總限制a取正值。相應地，容許性條件變為：

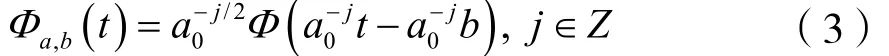
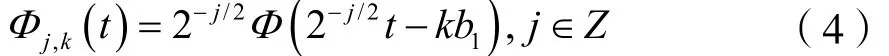
將b1進一步歸一化處理，得到：

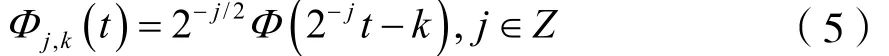
一般情況下，離散小波函數有：

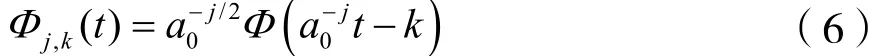
而離散化小波變換系數為：

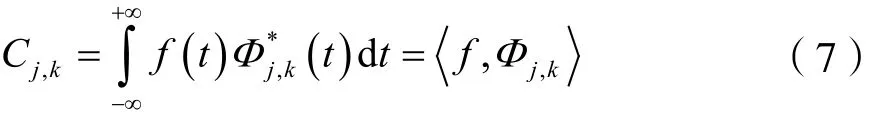
其重構公式為：

1.2 相關去噪算法

相關去噪法利用信號和噪聲在不同尺度間相關性不同的特點，將相鄰尺度的小波系數做相關處理，然后根據相關程度決定是否保留小波系數，再重構信號達到去噪目的[11]。相關去噪法的優點在于對信噪比高的信號去噪效果較好，對信號邊沿保護較好，且不會產生閾值法的邊緣過于平滑和Gibbs現象。缺點在于，若計算相關系數的點偏移量較大，則相關系數受影響，將對大尺度相關系數的計算帶來更大誤差，且需要迭代運算，不僅計算量大，而且需要預估噪聲的方差來確定迭代終止條件。

設帶噪信號長度為l，分解層數為j，則w( j,n)表示分解后第j層第n點的小波系數。依次從各層小波系數中選取一段不包含信號的噪聲（通常選取開始的一段）長度記為l1，并估計噪聲的方差δn，將相鄰尺度的小波相關系數歸一化處理，將其絕對值與當前尺度的小波系數作比較。若絕對值較大，則認為是由信號引起的，將轉移原系數并置零處理；否則，保留原系數，直到原系數的能量接近于噪聲能量為止。

具體步驟如下：

（1）對帶噪信號進行二進制離散小波變換；

（2）求相鄰尺度的小波系數的相關系數Cw(j,n)（最后一層不做相關處理），并作歸一化處理；

（4）重復步驟（3），直到該尺度內滿足：

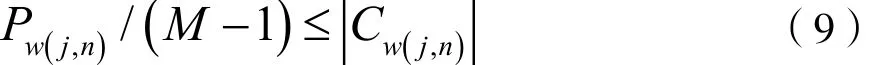
其中，Pw(j,n)為w( j,n)的功率，定義w( j,n)與w( j+1,n)的相關系數為cor( j,n)，則：

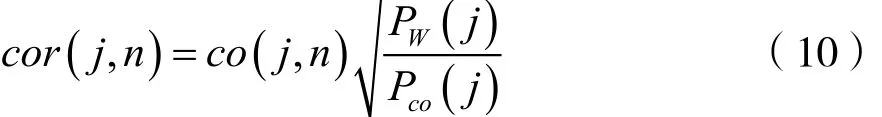
其中：

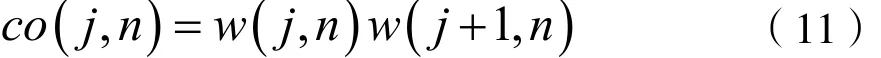
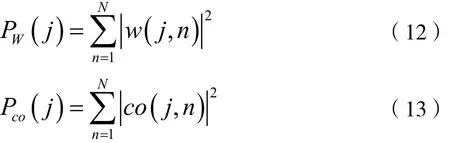
1.3 閾值函數

1.3.1 硬閾值去噪

硬閾值去噪由Donoho提出，思路如下：

（1）對含噪信號做小波變換，得到對應小波系數w( j,n)。

（2）閾值函數為：

其中δ為噪聲功率，N為小波變換點數。若|w( j,n)|≥T，保留原系數；否則，置零處理。

（3）將采用閾值處理過的小波系數重構，即為去噪后的信號，具體表達式如下：

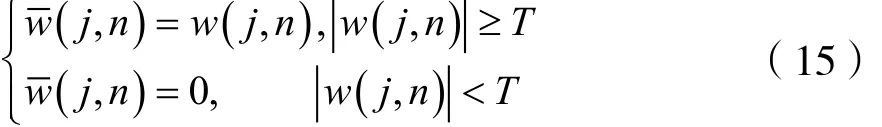
1.3.2 軟閾值去噪

在硬閾值基礎上將較大的小波系數做收縮處理，得到：

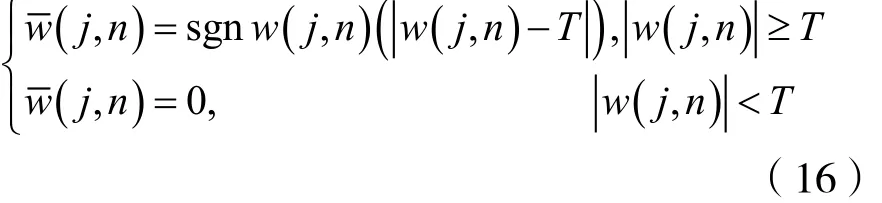
圖1 軟硬閾值函數的比較

硬閾值處理使得信號不連續[12]，采用軟閾值函數處理后的信號相對于硬閾值更加平滑，但也由于對較大的小波系數進行了收縮處理而帶來了偏差，使得信號丟失了某些特征。

1.4 改進的相關閾值去噪算法

若帶噪信號長度為l，分解層數為j，估計噪聲的方差為δn，小波分解點數為N，根據式（14）求得全局閾值T，由式（11）計算第j層小波系數w( j,n)與第j+1層小波系數w( j+1,n)的相關系數，并歸一化得到co( j,n)。設改進新閾值變量為λ，其中：

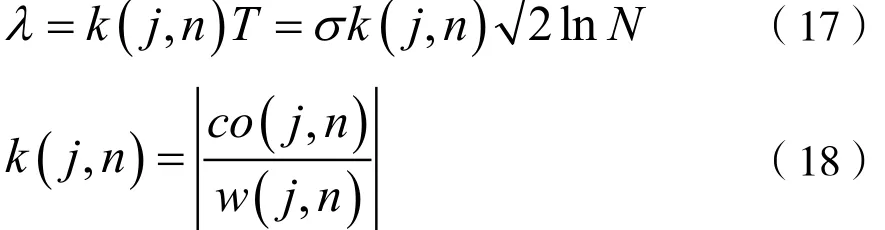
相比于常規閾值函數去噪法，此處相關系數當信號與噪聲幅度相近時，不會將信號作為噪聲去除，保證了小波系數的有效性。在此基礎上引入軟閾值進行去噪，改進的軟閾值函數必須滿足條件：當小波系數趨近于λ時，閾值函數w—( j,n)趨近于w( j,n)或0。

閾值函數w—( j,n)關于w( j,n)為增函數，且逐漸遞增時趨近于w( j,n)。

基于上述理論，設計閾值函數公式為：

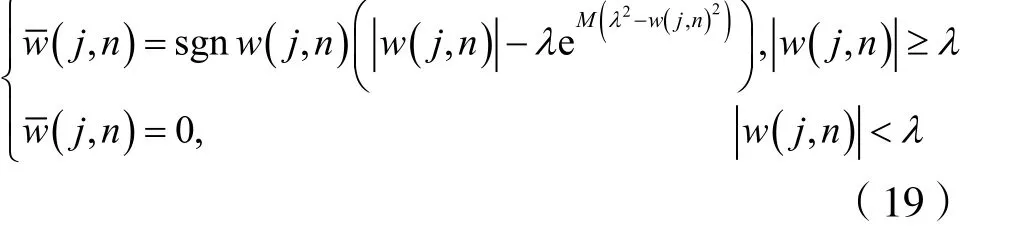
此閾值函數具有連續性，且在|w( j,n)|≥λ時高階可導。相關系數的引入，使得信號成分進一步加強，而噪聲成分得到削弱，并減少了有效信號缺失的狀況。此外，可調節參數M的引入，使得去噪函數適應各種情況。當信噪比較大時，可以適當加大M值，范圍通常設定在0.1～1。

2 結果比較

選取一段正弦波信號并加入噪聲，使得信噪比SNR=5 dB。采用相關法和改進的相關閾值函數法對含噪信號去噪處理，并計算信噪比。小波分解至5層，采用sym8小波基，結果如圖2所示。

選取水聲信號中的聲信標信號作為仿真模型，其特征為高頻窄脈沖。使用Matlab構造仿真信號，信號長度l=10 s，頻率fs=37.5 kHz，周期T=1 s，波形為正弦波，加噪后信噪比為0 dB。同樣，小波分解至5層，采用sym8小波基仿真，結果如圖3、圖4所示。

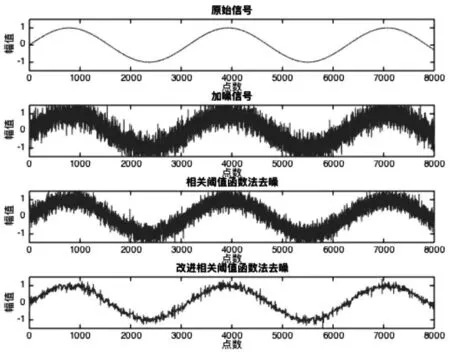
圖2 兩種算法去噪情況比較

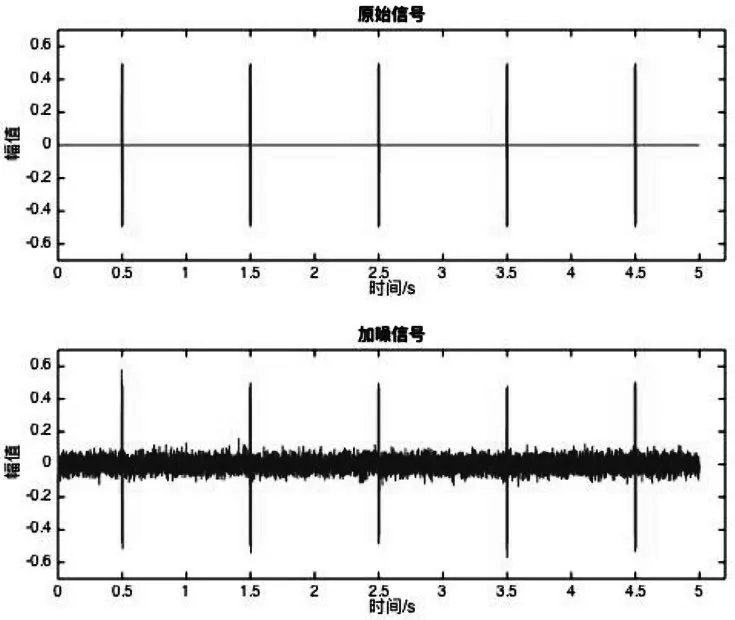
圖3 原始信號和加噪信號

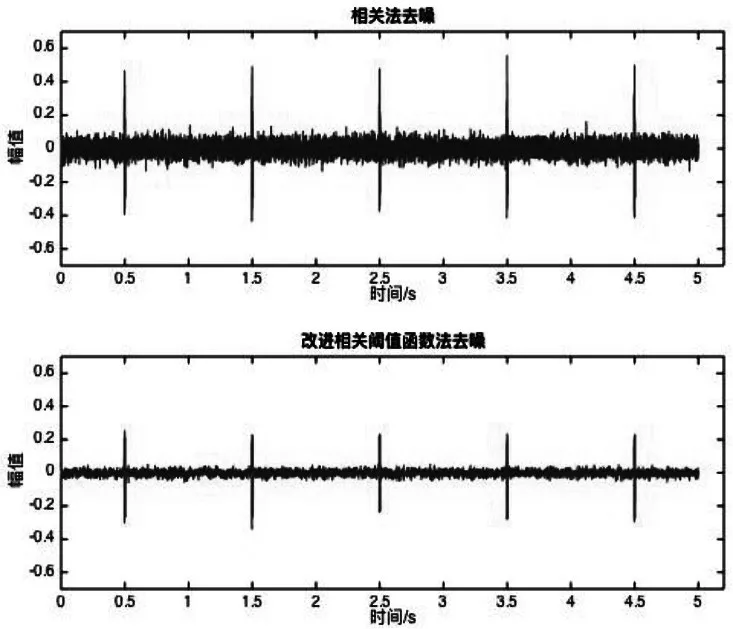
圖4 去噪后的信號

通過對比可以看出，相關去噪法去噪后依然保留了很多尖刺，起伏較大，而改進的相關閾值去噪法去噪明顯，波形較為平滑。為進一步說明去噪效果，對上述兩種信號去噪前后的信噪比和均方誤差進行了比較，結果如表1、表2所示。

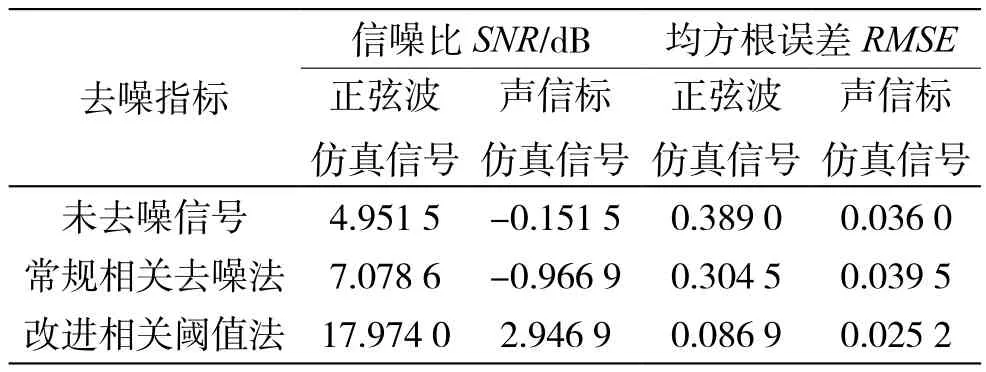
表1 兩種去噪方法去噪效果對比

從表1可以看出，改進相關閾值法均方誤差更小，能夠穩定提高信噪比，效果優于常規相關去噪法，而相關去噪法在提高信噪比的同時，甚至出現了均方根誤差不穩定的情況。此外，通過調整可調因子M值（如表2所示）發現，當設定值M在0.1～1，算法具有較好且穩定的性能。因此，所提出的改進相關閾值函數去噪法優于常規相關去噪法。

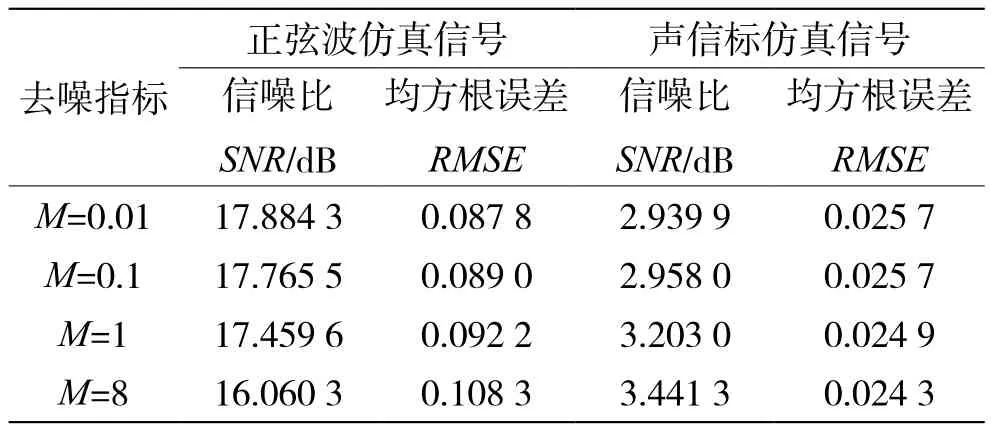
表2 可調因子去噪效果分析

聲信標信號為f=37.5 kHz的脈沖信號，周期T=1 s。選取一段海底深度1 900 m的聲信標信號進行去噪處理，結果如圖5所示。

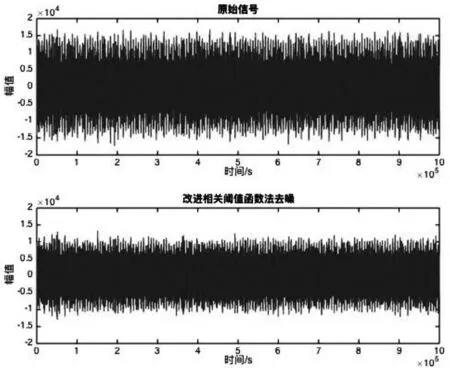
圖5 聲信標數據處理消噪結果

從圖5可以看出，深度1 900 m的聲信標信號已被噪聲完全湮沒，且不能直接分辨出信號。經本文所提方法處理后，抑制了部分噪聲，改善了信噪比，為后續處理步驟奠定了基礎。

3 結 語

基于常規小波空域相關算法的優勢，本研究利用多尺度間小波系數相關性，結合軟閾值去噪算法原理，提出了一種新型相關閾值去噪方法。經仿真分析，本研究提出的改進算法去噪效果優于常規小波空域相關去噪算法，能在最大程度保留原信號小波系數，同時平滑信號，且信號邊沿信息完整，具有更高的信噪比和更小的均方根誤差。因此，所提去噪方法非常適用于水聲信號的去噪。

[1] 惠俊英,生雪莉.水下聲信道[M].哈爾濱:哈爾濱工程大學出版社,2011.HUI Jun-ying,SHENG Xue-li.Underwater Acoustic Channel[M].Harbin:Harbin Engineering University Press,2011.

[2] 劉鯖潔,陳桂明.FFT和小波變換在信號降噪中的應用[J].數據采集與處理,2009,24(b10):58-60.LIU Qing-jie,CHEN Gui-ming.The Application of FFT and Wavelet in Signal Denoising[J].Data Acquisiton and Processing,2009,24(b10):58-60.

[3] 向東陽,吳正國,侯新國.改進的多小波變換系數相關去噪算法[J].高電壓技術,2011,37(07):1728-1733.XIANG Dong-yang,WU Zheng-guo,HOU Xin-guo.An Improved Multi Wavelet Transform Correlation Denoising Method[J].High Voltage Techni-que,2011,37(07):1728-1733.

[4] Donoho D L.De-noising by Soft-thresholding[M].IEEE Press,1995.

[5] 劉娟花,李福德.基于小波變換的信號去噪研究[J].西安理工大學學報,2004,20(03):289-292.LIU Juan-hua,LI Fu-de.The Reaserch of Signal Denoising Based On Wavelet Transform[J].Journal of Xi’an University of Technology,2004,20(03):289-292.

[6] 厲茜.基于相關模型的平穩小波維納濾波器圖像去噪算法[D].長春:吉林大學,2004.LI Qian.The Image Denoising Algorithm of Stable Wavelet Wiener Filter Based on Correlation Model[D].Changchun:Jilin University,2004.

[7] 肖倩,王建輝,方曉柯等.一種基于互相關函數的小波系數相關閾值去噪方法[J].東北大學學報:自然科學版,2011,32(03):318-321.XIAO Qian,WANG Jian-hui,FANG Xiao-ke,et,al.A Denoising Method Based on Wavelet Coefficient Correlation Threshold of Mutual Correlation Function[J].Journal of Northeastern University(Natural Science Editon),2011,32(03):318-321.

[8] Xu Y,Weaver J B,Healy D M,et al.Wavelet Transform Domain Filters:a Spatially Selective Noise Filtration Technique[J].IEEE Transactions on Image Processing a Publication of the IEEE Signal Processing Society,1994,3(06):747-758.

[9] Daubechies I.Ten lectures on Wavelets[M].Capital City Press,1992.

[10] Mallat S.A Wavelet Tour of Signal Processing[J],The Sparse Way,1999,31(03):83-85.

[11] Zhang L,Bao P.Denoising by Spatial Correlation Thresholding[J].IEEE Transactions on Circuits &Systems for Video Technology,2003,13(06):535-538.

[12] 張仁輝,杜民.小波分析在信號去噪中的應用[J].計算機仿真,2005,22(08):69-72.ZHANG Ren-hui,DU Min.Application of Wavelet Analysis in Signal Denoising[J].Computer Simulation,2005,22(08):69-72.