基于壓縮傳感的高精度同步相量測量方法
于華楠,杜 瑤,郭樹旭
(1.東北電力大學 信息工程學院,吉林省 吉林市132012;2.吉林大學 電子科學與工程學院,長春 130012)
0 引 言
廣域測量系統(Wide area measurement system,WAMS)作為電網動態實時監測的新技術和重要手段,能實時地反映全網系統的動態變化,對電網的安全穩定運行起到了重要的作用[1]。而基于GPS技術的同步相量測量單元(Phasor measurement unit,PMU)正是WAMS系統的核心與基礎[2,3],并已被廣泛應用在電網中以獲得電網的實時動態變化,為實現電力系統動態監測提供了可能。
目前,國內外學者提出了多種同步相量測量算法,主要包括離散傅里葉變換(Discrete Fourier transform,DFT)法[4]、過零點檢測法(Zero crossing technique)[5]和數字濾波器法[6,7]等。其中,由于DFT算法適用于快速運算,且具有良好的諧波抑制特性,在靜態條件下具有較好應用價值,而被廣泛應用到同步相量測量中。但在非同步采樣的情況下,現有的DFT算法往往會在幅值和頻率測量上出現誤差,且誤差會隨著非同步性的增強而急劇增大,導致出現頻譜泄露和柵欄效應,使溫測量結果達不到實際應用的要求[8]。因此,這種誤差使DFT算法存在一定的局限性,降低了相量測量的準確度,以至于直接影響到WAMS的應用效果。同步相量的不準確測量最終將導致電網的動態安全監控能力下降,嚴重時將影響電網的安全穩定運行[9]。
本文將壓縮傳感理論與DFT算法相結合,在無顯著延長總觀測時間的條件下,改善了算法性能,實現了對信號的精確測量,為同步相量測量裝置(Phasor measurement unit,PMU)的實現打下了良好基礎。
1 相量測量基本原理
同步相量測量裝置(Phasor measurement unit,PMU)是用于同步相量的測量與輸出,并進行動態數據記錄的裝置[10,11]。PMU的基本原理為:首先由GPS接收器輸出1 PPS信號,經過鎖相振蕩器后,信號被劃分成一定數量的脈沖用于采樣,再對信號進行濾波,然后經數模(A/D)轉換器量化,最后按照離散傅里葉變換原理,經微處理器計算出相量[12]。PMU裝置是電力系統實時動態監測的重要組成部分,因此,其必須具有較高的精確度和可靠性,確保電力系統運行處于安全、穩定的狀態,同時保障數據測量的精度。PMU的典型結構如圖1所示。

圖1 PMU結構圖Fig.1 Structure of PMU
在實際測量時,電網頻率總是在工頻(50 Hz)附近波動,使系統頻率和采樣頻率不能同步,造成非同步采樣,導致出現頻譜泄露和柵欄效應,影響系統測量精度。因此,為消除或減小由于非同步采樣造成的DFT測量誤差,本文提出了一種基于壓縮傳感的修正離散傅里葉變換的同步相量測量算法。
2 CS-DFT算法
2.1 壓縮傳感理論
壓縮傳感(Compressed sensing,CS)理論是由Donoho等[13,14]提出的一種新型的信息獲取指導理論。該理論指出:對可壓縮的信號可通過遠低于奈奎斯特標準的方式進行數據采樣,仍能精確地恢復出原始信號。壓縮傳感的優點在于信號的投影測量數據量遠遠小于傳統采樣方法所獲得數據量,突破了奈奎斯特采樣定理的瓶頸,使得高分辨率信號的采集成為可能。
壓縮傳感理論主要包括3個方面:稀疏表示、編碼測量和重構算法。圖2為壓縮傳感理論的基本框架。

圖2 壓縮傳感理論基本框架Fig.2 Basic framework of compressed sensing theory
下面從這3個方面對壓縮傳感理論進行分析:
設測量信號為x∈Rn×1,其中n為信號長度,對x進行壓縮傳感的過程如下。
(1)稀疏表示:信號的稀疏變換就是信號必須在某種變換下稀疏表示,這是壓縮傳感的先驗條件。設計過完備字典D={D1,D2,…,Dn},使信號x在過完備字典上具有稀疏性,即:
x=Da
(1)
式中:a是稀疏變量。
(2)編碼測量:在編碼測量中最重要的一步是確定投影矩陣,為了確保信號的線性投影能夠保持信號的原始結構,投影矩陣必須滿足約束等距性(Restricted isometry property,RIP)條件。設觀測矩陣為Φ∈Rm×n(m?n),則測量向量為y=Φx。
(3)信號重構:先運用重構算法由測量值及投影矩陣重構原始信號,即從測量向量y中恢復出原始信號x,然后利用重構算法求解最優問題min‖x‖,s.t.y=Φx。
2.2 信號的建模
本文以信號的標準形式為出發點,來表示不同特征的電力信號[15]:
s(t)=Acos(?t+φ)
(2)
式中:?為角頻率;φ為初相角;A為幅值,其利用歐拉公式可以展開為:
(3)
由于實際同步相量測量信號能夠通過多個正弦波疊加的形式來表示,因此可利用復指數形式表示為:
(4)
式中:Ah為正弦信號的幅值;φh為相角;fh為第h個波形分量的頻率值,且fh=h·f0,其中f0為基波頻率,h為正弦波的個數;t為時間。
現給定長度為N的樣本序列,對其進行DFT算法處理,可得到一組相應的N個頻域系數,即:

(5)
式中:k為采樣點數,0≤k (6) 式中:v為離散歸一化頻率。 為提高同步相量測量算法的頻率分辨率,由頻率分辨率的定義: (7) 可知,首先引入插值因子P(P為一個大小合適的整數),使N′=PN,以此使算法具有高頻率分辨率,即: (8) 式中:N為采樣點數;T為采樣間隔。 由此,同步相量測量信號的歸一化頻率為: (9) (10) (11) 0≤k 為了使同步相量的測量運算起來更加簡單、直觀,可將式(8)寫成更緊湊的矩陣形式: s≈Da (12) 式中:s為包含同步相量測量信號DFT系數的向量;D為N×N′維矩陣;a為包含同步相量測量信號的相量值的向量,且由于a中大多數元素均為零,因此,可認為a具有稀疏性。 在實際測量測量中,還需要考慮噪聲等不定因素,因此,式(12)為: X=s+n=Da+e (13) 式中:X為原始測量向量;e為噪聲信號。 因此,由上述分析可知,可將該問題看作為壓縮傳感問題,即考慮將CS方法與DFT算法相結合應用于同步相量測量中。其中,用CS理論解求解(13)的表示如下: (14) 式中:‖a‖0是l0的范數,即a的非零元素的個數;ε為給定的閾值。 引入矩陣DSt,其僅由以下算法步驟選擇的D矩陣的列組成,最初DS0有零列。該迭代計數器設置t=1。 步驟2 查找索引lt,使得: (15) 式中:上標H表示復共軛轉置矩陣;rt-1為殘差值;t為迭代次數。這一步迭代覆蓋了該算法的索引恢復部分。 步驟4 計算一個新的向量: (16) 式中:t是非零元素。這一步的迭代提供了逐步細化的估計。 總的來說,CS-DFT算法是壓縮傳感與DFT算法的融合。首先利用離散傅里葉變換對測量信號進行稀疏化,再通過狄利克雷函數來構造觀測矩陣,最后,OMP算法在稀疏矩陣約束范圍內搜索最優的匹配原子,提取特征信息,最后重構出原測量信號,為同步相量測量的進一步分析實驗奠定了良好的基礎。 本文采用基波頻率為50 Hz的同步相量測量信號,信號采樣點數為1024個,采樣頻率為5.12 kHz,時間為0.2 s,對測量信號進行分析,總結其基本特征,構建典型測量信號的數學模型,包括諧波和間諧波信號、頻率斜升信號、幅度和相位調制信號,以及幅度和相位階躍信號,如圖3所示。 圖3 測量信號模型Fig.3 Model of measurement sign 目前,衡量相量測量單元(PMU)性能的主要指標有兩種:一是采用幅度誤差和相位誤差分別評價的方法;二是采用綜合矢量誤差(Total vector error,TVE)來評價同步相量測量裝置的測量誤差[15]。但由于TVE指標更為科學、全面,可同時反映相量誤差和幅度誤差,因此,本文采用TVE評價方法。 TVE定義如下: (17) 式中:XR為理想信號相量的實部;XI為理想信號相量的虛部;XR(n)為實測相量的實部;XI(n)為實測相量的虛部。 利用本文方法對典型測量信號進行MATLAB仿真實驗,得到其DFT分析和CS-DFT分析。 (1)在本次實驗中,以相位調制信號和相位階躍信號為例,其中,相位調制信號的采樣頻率為5.12 kHz,載波頻率為100 Hz,采樣點數為1024個,信號頻率為40 Hz;相位階躍信號的采樣頻率為5.12 kHz,采樣點數為1024個,信號頻率為50 Hz,實驗對比結果分別如圖4、圖5所示。 圖4 相位調制信號的DFT和CS-DFT分析Fig.4 DFT and CS-DFT analysis of phasemodulation signal 圖5 相位階躍信號的DFT和CS-DFT分析Fig.5 DFT and CS-DFT analysis of phase step signal 由圖4和圖5可以看出,本文CS-DFT方法能夠有效地消除或減弱現有基于離散傅里葉變換的同步相量測量裝置中普遍存在的頻譜泄露和柵欄效應,提高了相量測量的準確度,減小了測量誤差,為WAMS系統打下了良好的基礎,為實現電力系統動態監測提供了可能。 (2)在本次實驗中,分別用DFT和CS-DFT兩種算法對信號進行相量測量,得到各時刻的TVE值如圖6、圖7所示,其中以相位調制信號為例,時間為0.5 s,采樣點數為1024個,采樣頻率為5.12 kHz。圖6為在相位調制信號下的傳統DFT算法的TVE值,圖7為在相位調制信號下的CS-DFT算法的TVE值。 圖6 相位調制信號下DFT算法的TVE值Fig.6 TVE of DFT under phase modulation signal 圖7 相位調制信號下CS-DFT算法的TVE值Fig.7 TVE of CS-DFT under phase modulation signal 由圖6和圖7可明顯看出,DFT算法和CS-DFT算法的TVE值分別控制在0.6%和0.14%以下,TVE值均在合理范圍內,且CS-DFT算法的TVE值均小于DFT算法,由此可證明兩種算法均能滿足相量測量的要求,CS-DFT算法的性能更優。 (3)為進一步證明CS-DFT算法的測量精度和通用性,使測量結果更加準確,在本次實驗中,以實際獲取的工頻測量信號為例,如圖8所示。 顯而易見,該工頻測量信號含有干擾信號,對其分別用DFT和CS-DFT兩種算法進行分析實驗,得到各時刻的TVE值如圖9所示。 圖8 工頻測量信號Fig.8 Power frequency measuring signal 圖9 工頻測量信號下DFT和CS-DFT算法的TVE值Fig.9 TVE of DFT and CS-DFT under power frequencymeasuring signal 由圖9可明顯看出,在對不同測量信號進行MATLAB仿真實驗時,CS-DFT算法的TVE值均小于DFT算法,由此得出結論,CS-DFT算法指標優于DFT算法,CS-DFT算法對測量信號實現了精度更高的測量。 本文提出一種基于壓縮傳感理論的同步相量測量方法,該方法可對測量信號的同步相量進行準確、有效的測量,同時可明顯消除或減小由于非同步采樣造成的離散傅里葉變換的測量誤差,在很大程度上改善了傳統DFT算法的測量精度,能夠滿足WAMS系統的相關標準及要求,為實現電力系統動態監測和安全穩定運行提供了有力的保障。 [1] 李建,謝小榮,韓英鐸. 同步向量測量的若干關鍵問題[J]. 電力系統自動化,2005,29(1):45-48. Li Jian, Xie Xiao-rong, Han Ying-duo. Key issues of the synchronized vector measurement [J]. Automation of Electric Power Systems, 2005, 29(1):45-48. [2] 吳京濤,謝小榮,王立鼎,等. 廣域測量系統在電力系統的發展與展望[J]. 電力設備,2006,7(3):26-29. Wu Jing-tao, Xie Xiao-rong, Wang Li-ding, et al. Wide Area Measurement System Development and Prospect in the power system [J]. Electric Power Equipment, 2006, 7(3):26-29. [3] Alasti H. Non-uniform-level crossing sampling for efficient sensing of temporally sparse signals [J]. Wireless Sensor Systems, 2014, 4(1):27-34. [4] 王茂海,孫元章. 基于DFT的電力系統相量及功率測量新算法[J]. 電力系統自動化,2005,29(2):20-24. Wang Mao-hai, Sun Yuan-zhang. A DFT-based method for phasor and power measurement in power systems [J]. Automation of Electric Power Systems, 2005, 29(2):20-24. [5] 周捷,陳堯,崔建中. 母線電壓同步相角測量算法研究及實現[J]. 繼電器,2002,30(3):13-16. Zhou Jie,Chen Yao,Cui Jian-zhong. Study and implementation of the algorithm for bus synchronized voltage phase angle measurement [J]. Relay,2002,30(3):13-16. [6] Kamwa I, Samantaray S R, Joos G. Compliance analysis of PMU algorithms and devices for wide-area stabilizing control of large power systems [J]. IEEE Trans on Power Systems, 2013, 28(2):1766-1778. [7] 汪芙平,靳夏寧,王贊基. 實現動態相量測量的FIR數字濾波器最優設計[J]. 中國電機工程學報,2014,34(15):2388-2395. Wang Fu-ping, Jin Xia-ning, Wang Zan-ji.Optimal design of FIR digital filters for dynamic phasor measurement[J]. Proceedings of the CSEE, 2014, 34(15):2388-2395. [8] 徐建源,王亮,林莘,等. 基于遞推DFT同步相量測量算法的研究[J]. 高壓電器,2011,47(11):40-44. Xu Jian-yuan, Wang Liang, Lin Shen, et al. Based on recursive DFT phasor measurement algorithm [J]. High Voltage Apparatus, 2011, 47(11):40-44. [9] 丁濤,董柏峰,顧偉,等. 基于PMU的電壓穩定動態線性化指標優化切負荷算法[J]. 電力系統保護與控制,2013,41(9):27-33. Ding Tao, Dong Bai-feng, Gu Wei, et al. Optimization of a load shedding scheme using dynamic voltage stability linearized index based on PMU [J]. Power System Protection and Control, 2013, 41(9):27-33. [10] Faiz J, Lotfi-fard S, Shahri S H. Prony-based optimal bayes fault classification of overcurrent protection [J]. IEEE Transactions on Power Delivery, 2007, 22(3):1326-1334. [11] Mai R K, He Z Y, Fu L, et al. A dynamic synchrophasor estimation algorithm for online application [J]. IEEE Transactions on Power Delivery, 2010, 25(2):570-578. [12] 畢天姝,劉灝,楊奇遜. PMU 算法動態性能及其測試系統[J]. 電力系統自動化,2014,38(1):62-67. Bi Tian-shun, Liu Hao, Yang Qi-xun. PMU algorithm and dynamic performance test system [J]. Automation of Electric Power Systems, 2014, 38(1):62-67. [13] Donoho D L. Compressed sensing [J]. IEEE Transactions on Information Theory, 2006, 52(4):1289-1306. [14] Donoho D L, Tsaig Y. Extensions of compressed sensing[J]. Signal Processing, 2006, 86(3):533-548. [15] C37.118—2005. IEEE standard for synchrophasors for power systems[S].2.3 算法實現




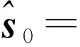
3 仿真實驗
3.1 測量信號模型

3.2 算法性能評價
3.3 仿真實驗及結果分析
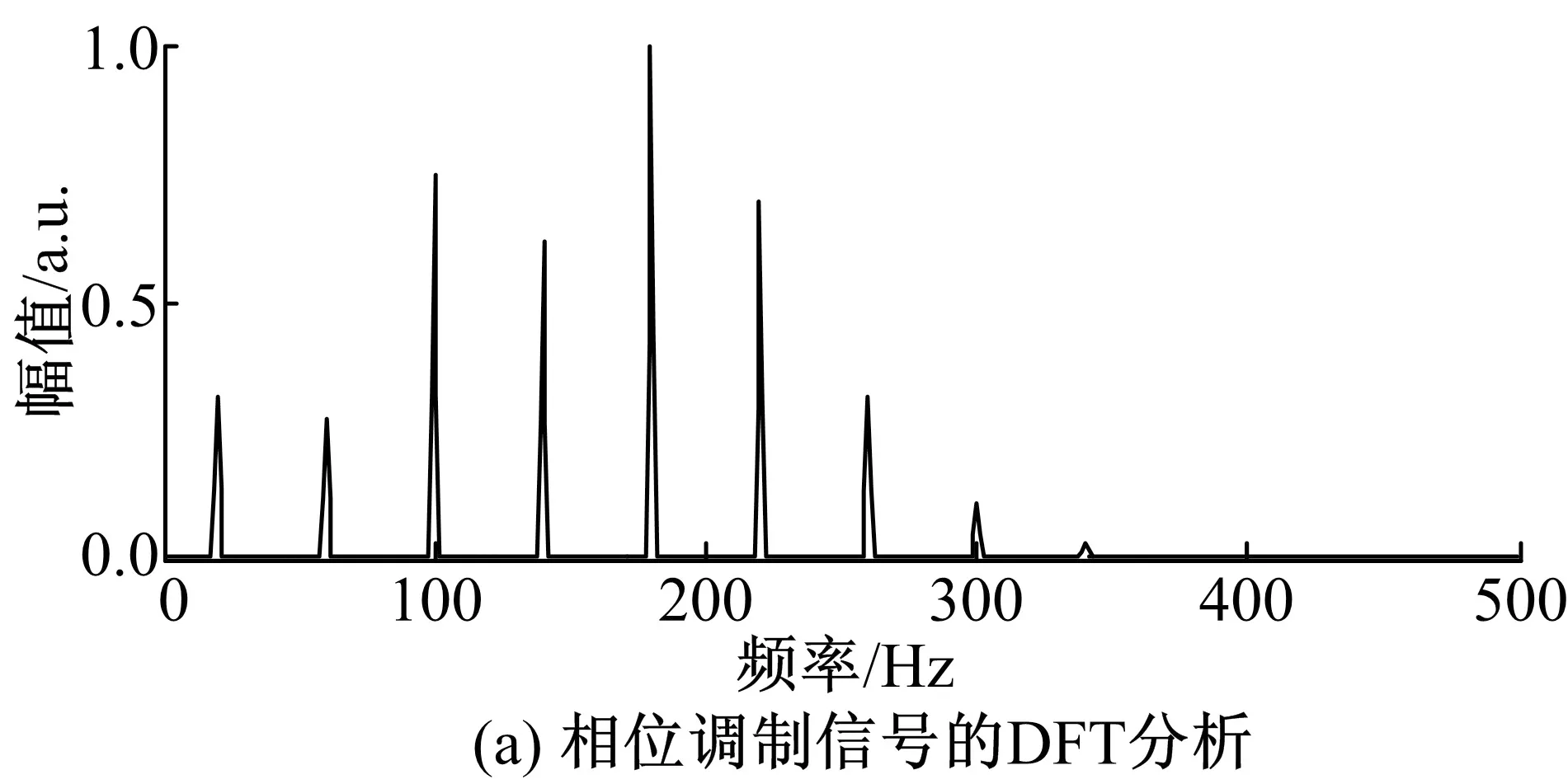





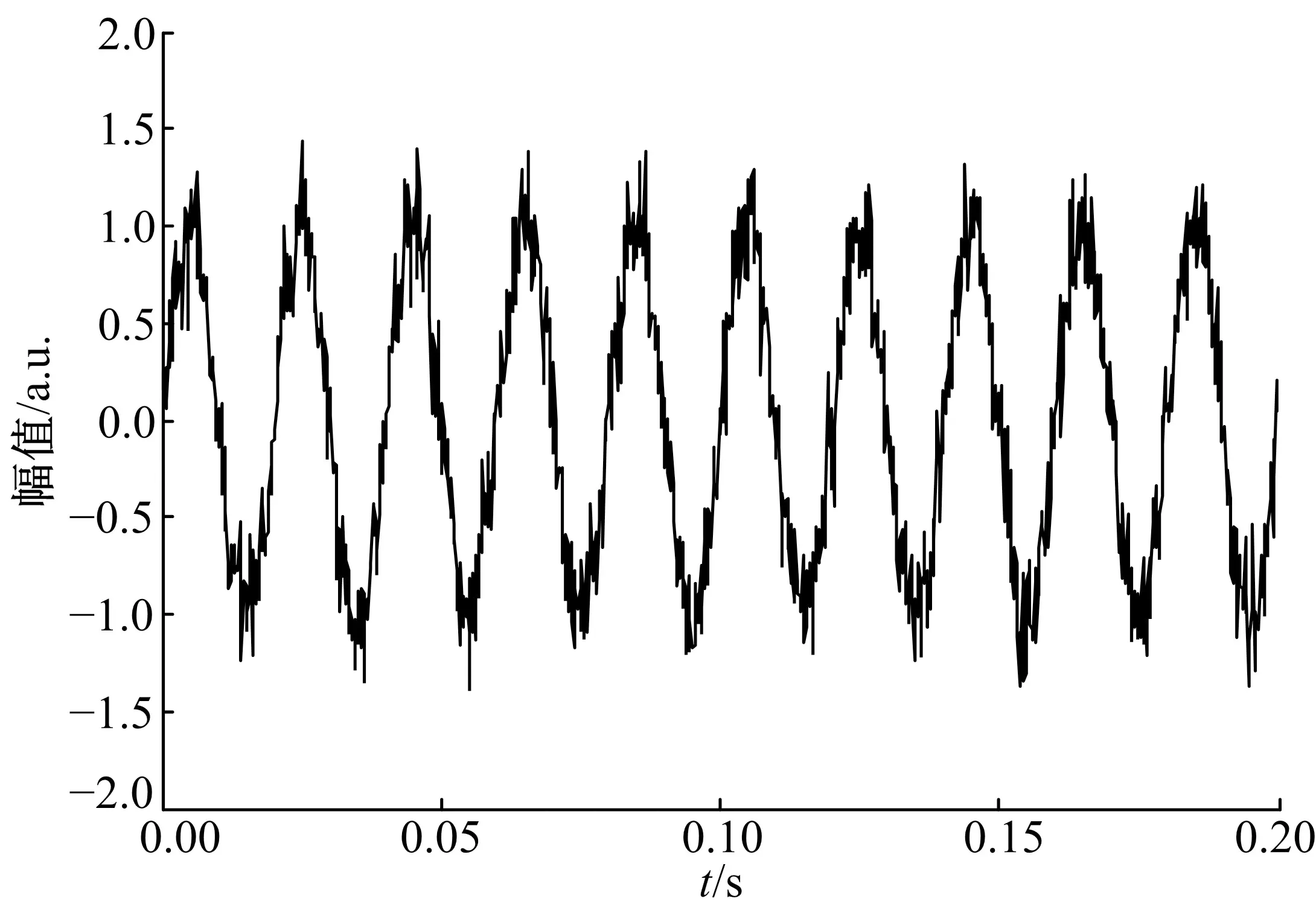

4 結束語

