基于半陷門單向函數的公鑰密碼
趙 博, 秦貴和, 趙永哲, 楊文迪
(1.吉林大學 計算機科學與技術學院,長春 130012;2.華東師范大學 計算機科學與軟件工程學院,上海 200062)
0 引 言
1976年,Diffie和Hellman[1]發表了著名文章《密碼學的新方向”,文章引入了“公鑰密碼”的概念,并提出基于“陷門單向函數(Trapdoor one-way function)”來構造公鑰密碼的思想。不久,第一批公鑰密碼方案便被提了出來,它們分別是Merkle和Hellman基于背包問題的MH密碼體制[2]以及Rivest、Shamir和Adelman基于整數分解問題的RSA密碼體制[3]。隨后Rabin、ElGamal、ECC等公鑰密碼體制也相繼問世。
進入到21世紀,現有公鑰密碼(RSA、ElGamal、ECC等)日益受到量子計算的威脅[4,5],為了應對挑戰,國際密碼學界提出了“后量子密碼學(Post-quantum cryptography,PQC)”的新學科方向。PQC的主要目標便是研究能抵抗量子計算的公鑰密碼(Quantum resistant public key cryptography),目前主要基于量子計算機不擅長計算的數學難題(比如NPC問題)來設計密碼,該類密碼主要有如下幾個研究方向:基于格上困難問題的密碼[6]、基于糾錯碼譯碼問題的密碼[7]、基于多變量的密碼[8]、基于辮子群(Braid Group)的密碼[9]以及基于背包問題的密碼[2,10]。
但目前所提出的抗量子計算公鑰密碼方案中的絕大多數都已被證明是不安全的。盡管不斷有新方案被提出,但從構造方法來看,這些方案不外乎兩大類:其一是基于“陷門單向函數”,這類公鑰密碼占絕大多數,其關鍵在于如何設計陷門。其二則是基于“非對稱密鑰交換”,其關鍵在于如何實現非對稱的密鑰交換,這往往要用到“單向函數”。一般說來,尋找單向函數要比尋找陷門單向函數容易得多,但單向函數不可逆,故不能直接用來實現公鑰密碼。而利用陷門單向函數雖可直接實現公鑰密碼,但由于“陷門性”和“單向性”的固有矛盾,使得二者很難兼顧。為了構造陷門,就必然要犧牲單向性;反之亦然。
本文重點研究了如何設計實現半陷門單向函數,以及如何基于半陷門單向函數來構造公鑰密碼。
1 半陷門單向函數的設計與實現
為了同時兼顧陷門性和單向性,本文引入了“半陷門單向函數(Semi-trapdoor one-way function,STOF)”的概念,其定義如下:
定義1 “半陷門單向函數”是一族“半可逆”的陷門函數:ft:X→Y,滿足:
(1)已知ft和x∈X,計算y=ft(x)是容易的。

由于半陷門單向函數分別涉及單向性和陷門性,所以在設計時要同時對二者進行構思,這就需要選擇合適的困難問題。為便于描述,文中常用的術語和基本符號如表1所示。

表1 基本符號
1.1 子集和問題與背包密碼
“子集和問題(Subset sum problem,SSP,)”是“0-1背包問題”的一個特例。其定義如下:
SSP是著名的NPC問題。大多數背包密碼都是基于SSP來構造的。為了保證解密的唯一性,公鑰背包向量還必須滿足USS(Unique Subset Sum),即唯一子集和條件。但已有的的背包密碼通常無法抵御“低密度攻擊”,背包向量的“密度”定義如下:

由文獻[11-13],若DA>1,則A通常不滿足USS條件。事實上,很多USS背包向量的密度都?1。早期算法[14]可破解密度小于0.6463的背包密碼,改進后算法[15]則可破解密度小于0.9408的背包密碼。故為了抵御低密度攻擊,公鑰背包除應滿足USS條件外,還應具有高密度(大于0.9408),但這二者往往很難兼顧,這也是設計背包密碼的難點所在。
若DA<1∧DA≈1,則A中SSP通常有唯一解。而若DA>1∧DA≈1,則A中SSP通常有多解。這兩種情形均易受到基于格的攻擊[16,17]。只有當DA≈1時,對A中SSP無有效的解法。Impagliazzo和Naor亦證明,當DA=1時,求解A中SSP是最困難的[18]。多年來,對SSP最快的通用解法仍是Schroeppel和Shamir在1981年提出的[19],算法的時空復雜度分別為O(n·2n/2)和O(n·2n/4)。最近才有人對其進行了優化[20],但改進算法仍是指數級的,只是將時間復雜度降為O(n·2n/3)。
若在[1,2n]中均勻隨機選擇A=(a1,…,an),則A通常是難解的。實驗發現,如此得到的A通常不滿足USS條件。實際上,當DA≈1時,判定A是否滿足USS條件亦是NPC問題[21]。
1.2 基于SSP的半陷門單向函數
可基于SSP的難解和易解性來設計半陷門單向函數。為此引入“半超遞增背包向量”的定義如下:

顯然,對于半超遞增背包向量,可快速求出其SSP解的后半部,且易證如下定理:

(1)A中SSP易解當且僅當A[1,n]中SSP易解。
(2)A為USS背包當且僅當A[1,n]為USS背包。
(3)若A[1,n]中SSP是難解的,則求解A中SSP的前半部亦是困難的。
基于半超遞增背包向量,可得半陷門單向函數ft:{0,1}2n→N的設計方案如下:
(1)選擇安全參數n;

(4)隨機選取M,W∈N+,其中:

(5)隨機選取(1,2,…,2n)的置換π,并用(π,M,W)對A模乘變換得B=(b1,b2,…,b2n),其中bπ(i)=Wai(modM);
(6)以t=(A,π,M,W-1)為陷門(A不用全保存,僅保存A[n+1,2n]即可),并將B公開;


1.3 ft的安全性分析


(1)



(2)


式中:m為滿足1 (3) 由式(3)可得等價的陷門t′=(A″,π′,M′,U),從而完全破解ft,其中: 由于B是直接由A經模乘變換所得,故可基于Lenstra關于固定變元數量的整數規劃問題可在多項式時間內求解,以及A的“半超遞增”性來破解(M′,U)[14,22]。而ft在該攻擊下是不安全的。 與MOOC融合的路徑選擇,是國內外圖書館界開展理論探討與實踐探索的重點內容。智力支持、技術支持、信息資源支持、實體空間支持,是圖書館與MOOC融合的4條主要路徑。從已有研究內容看,國內圖書館界主要側重論述通過開展版權服務、信息素養教育、嵌入課程輔導等提供智力支持,通過開展課程制作協助、學習者行為搜集分析與研判、MOOC平臺技術優化等提供技術支持來與MOOC進行融合。然而,目前國內支持MOOC發展的相關政策及法律環境尚不完善,圖書館現有智力資源、技術力量與MOOC的發展需要尚不匹配,圖書館所能提供的智力支持和技術支持與國內現階段MOOC發展的實際需求之間相差較遠。 改進思路是使(xπ(n+1),…,xπ(2n))不是由(xπ(n+1),…,xπ(2n))∈{0,1}n直接經模乘變換得到,而是由無明顯特征的背包向量經模乘變換得到,如此可使上述攻擊無效,改進方案如下: (1)選擇安全參數n。 (5)隨機選取Δ=(δ1,δ2,…,δ2n)∈{-1,0,1}2n,ω∈ZM;并用(M,Δ,ω)對A進行變換得C=(c1,c2,…,c2n)=A+Δ·ω(modM),即: ci=(ai+δiω)(modM)(i=1,2,…,2n)。 (6)隨機選取(1,2,…,2n)的置換π,并用(π,M,W)對C模乘變換得B=(b1,b2,…,b2n),即:bπ(i)=Wci(modM) (i=1,2,…,2n)。 (2)Fork=-n2Ton1Do S:=(SC-kω)(modM); Fori=2nDownto (n+1) Do If(S≥ai) Then xπ(i):=1; S:=S-ai; Else xπ(i):=0; EndIf EndFor Xk:=(xπ(n+1),…,xπ(2n)); 輸出Xk; EndIf EndFor (4) 由于半陷門單向函數不能單獨用來構造公鑰密碼。所以我們的方案構思是:以(ft,g)為公鑰,t為私鑰。這里ft:X→Y是半陷門單向函數,而函數g:X→Z則應滿足: (1)由g和x∈X,計算z=g(x)是容易的。 問題的關鍵是:對于給定的半陷門單向函數ft,如何構造滿足上述條件的函數g。 基于上述思路,本文給出了一種新的公鑰密碼方案,即STOF_PKC。STOF_PKC是基于第1節所構造的半陷門單向函數ft,以及F2上一個n×2n矩陣G來實現的,方案由密鑰生成、加密、解密三個算法構成,具體如下: 2.2.1 密鑰生成算法: (1)選擇安全參數n; (2)構造半陷門單向函數ft,其陷門t=(A,Δ,ω,π,M,W),輸出參數為B; (5)以t為私鑰,(B,G)為公鑰。 2.2.2 加密算法: 明文消息為x=(x1,x2,…,x2n)∈{0,1}2n{0},發送方對x加密過程如下: (1)獲得接收方的公鑰(B,G); (3)將密文(y,z)發送給接收方。 2.2.3 解密算法: (2)Fori:=1 TomDo EndFor (3)算法結束,所輸出者即為候選明文(集)。 由STOF_PKC的解密算法,易知: (1)若明密文之間是一對一的,則密文經解密后可唯一確定明文。 (2)若明密文之間是多對一的,則密文經解密后能得到一個明文集合,且該集合恰好包含與給定密文對應的所有明文。 (3)若密文不對應任何明文,則密文解密后得空集。 理想情形是每一個密文都僅對應唯一的明文,此時不僅可提高解密效率,還可保證解密的唯一性。令明文空間P={0,1}2n{0},則STOF_PKC滿足解密唯一性的充要條件是:不存在x,x′∈P(x≠x′)使ft(x)=ft(x′)∧G·x=G·x′。 設B的所有22n-1種非零子集和共有n_ss種取值,其中只與唯一子集和對應的取值共有n_uss種,則n_uss≤n_ss,且B滿足USS條件當且僅當n_uss=n_ss。顯然,若B滿足USS條件,則STOF_PKC必滿足解密唯一性。但這是NPC問題,無有效的判定算法。所以通過實驗來對此進行分析,實驗對不同的n,獨立生成10 000個ft實例,然后對DB、n_ss、n_uss計算平均值,并統計B滿足USS條件的出現數量,結果見表2。 表2 實驗結果 由實驗結果,可以看出: (5) 首先給出Semi-SSP(半子集和問題)的定義: (1)1≤i1 SSP和Semi-SSP的區別在于,前者對每個背包分量都要精確判定其是否屬于給定的“子集和”,而后者只需對一半背包分量進行精確判定。若SSP可解,則Semi-SSP必可解,反之亦然。即Semi-SSP也是NPC問題。關于STOF_PKC的安全性,有: 定理2 破解STOF_PKC等價于求解B中的Semi-SSP。 (6) (7) (8) 對于n>16,由 (9) k=16,…,n-1 可得: (10) (11) 本文引入了“半陷門單向函數”的概念,并給出了基于半陷門單向函數來構造公鑰密碼的思路。在此基礎上,給出了一種新的背包密碼方案STOF_PKC,并證明了破解STOF_PKC等價于求解B中的Semi-SSP。因此,若B中的Semi-SSP是難解的,則STOF_PKC便是安全的。但尚有一些新問題有待解決,比如是否存在其他實現半陷門單向函數的方法、是否存在其他基于半陷門單向函數的公實現簽名等,需要進行更深入的探索。 [1] Diffie W,Hellman M E. New directions in cryptography[J]. IEEE Transactions on Information Theory, 1976, 22:644-654. [2] Merkle R C,Hellman M E. Hiding information and signatures in trapdoor knapsacks[J]. IEEE Transactions on Information Theory, 1978, 24:525-530. [3] Rivest R L. A method for obtaining digital signatures and public-key cryptosystems[J]. Communications of the Acm, 1983, 26:96-99. [4] Shor P W. In algorithms for quantum computation: Discrete logarithms and factoring, foundations of computer Science[C]∥Proceedings on Symposium,Murray Hill,NJ,USA, 1994:124-134. [5] Grover L K. A fast quantum mechanical algorithm for database search[C]∥Proceedings of the Twenty-eighth Annual ACM Symposium on Theory of Computing,Philade lphia,PA,USA, 1996:212-219. [6] Poulakis D. On the cryptographic long term security[J]. Journal of Applied Mathematics & Bioinformatics, 2013,3(1):1-15. [7] Courtois N, Finiasz M, Sendrier N. In how to achieve a mceliece-based digital signature scheme[C]∥ International Conference on the Theory and Application of Cryptology and Information Security, Gold Coast, Australia, 2001: 157-174. [8] Porras J, Baena J, Ding J Zhfe.A new multivariate public key encryption scheme[Z].Post-Quantum Cryptogaphy,2014:229-245. [9] Dehornoy P. Using shifted conjugacy in braid-based cryptography[J]. Computer Science,2006,418:65-73. [10] Okamoto T,Tanaka K,Uchiyama S. Quantum public-key cryptosystems[J]. International Journal of Theoretical Physics, 2011, 51:912-924. [11] Elkies N D. An improved lower bound on the greatest element of a sum-distinct set of fixed order[J]. Journal of Combinatorial Theory, 1986, 41:89-94. [12] Guy R K. Unsolved Problems in Number Theory[M].New York-Berlin:Springer-Verlag,2001:17-35. [13] Kate A, Goldberg I. Generalizing cryptosystems based on the subset sum problem[J]. International Journal of Information Security,2011, 10:189-199. [14] Brickell E F. Breaking iterated knapsacks[C]∥Advances in Cryptology, Proceedings of CRYPTO’84, Santa Barbara, California, USA, 1984:342-358. [15] Coster M J,Joux A, Lamacchia B A, et al.Improved low-density subset sum algorithms[J]. Computational Complexity 1999, 2:111-128. [16] Joux A. A practical Attack Against Knapsack based Hash Functions (Extended )[M].Berlin Heidelberg:Springer,1994:58-66. [18] Impagliazzo R, Naor M. Efficient cryptographic schemes provably as secure as subset sum[J]. Journal of Cryptology,1996,9:199-216. [19] Schroeppel R, Shamir A. AT=O(2n/2),S=O(2n/4) algorithm for certain NP-complete problems[J]. Siam Journal on Computing, 1981,10(3): 456-464. [20] Li Qing-hua, Li Ken-li, Jiang Sheng-yi, et al. An optimal parallel algorithm for the knapsack problem[J]. Journal of Software, 2003, 14(14):891-896. [21] Christos H Papadimitriou. On the complexity of unique solutions[J]. Journal of the ACM, 1984, 31(2):392-400. [22] Shamir A. A polynomial time algorithm for breaking the basic Merkle-Hellman cryptosystem[J].IEEE Transactions on Information Theory,1984,30(5):699-704.

1.4 ft的改進方案









2 基于半陷門單向函數的公鑰密碼
2.1 方案構思


2.2 方案實現





3 分析驗證
3.1 STOF_PKC解密的正確性和唯一性分析









3.2 STOF_PKC的安全性分析
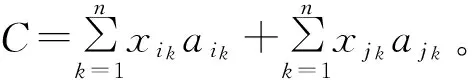






4 結束語

