新型擺線針輪行星減速器傳動系統的振動特性

陳忠敏，侯 力，段 陽，張 祺，楊忠學，蔣易強

(1. 四川大學 制造科學與工程學院，成都 610065；2. 四川建安工業有限責任公司 技術中心，四川 雅安 625000；3. 攀枝花學院 機械工程學院，四川 攀枝花 617000)

0 引 言

擺線針輪行星減速器具有傳動比變換范圍大、體積小、傳動精度高等特點，常用于替代兩級、三級傳動的普通圓柱齒輪減速器和圓柱蝸桿減速器。伴隨機器人、精密機械傳動、高新技術設備等行業需求的不斷提高，擺線針輪行星減速器的工作性能必將在苛刻的振動、噪聲和可靠性等技術標準要求下進一步提升。由于擺線針輪行星減速器的振動效應直接反映傳動系統的性能與工作可靠性，所以國內外學者對擺線針輪行星減速器的研究已從基礎靜力學向彈性動力學深入。Chen等[1]依據齒輪嚙合基本原理，推導出少齒差行星傳動的嚙合方程、嚙合副的共軛齒廓方程和接觸線方程等，并分析擺線輪與針齒的共軛嚙合特性，提出采用包絡法形成擺線軌跡的思路。Xu等[2]提出一種可精確預估擺線針齒動態嚙合對數、確定接觸點位置并獲取接觸載荷的動力學分析方法。Li[3]運用彈性接觸理論研究參數變化下的行星減速器運行中的接觸問題。Hsieh[4]研究擺線輪修形量對擺線針輪行星減速器動態性能的影響。Song等[5]通過數值仿真和實驗研究擺線針輪減速器的傳動特點以及針輪動態性能。李俊陽等[6]通過變形協調設計出漸開線少齒差行星傳動，利用仿真與實驗研究其空程回差、潤滑及動力學特性的改善情況。Sun等[7]研究擺線針輪行星減速器的針輪驅動情況以及應力的分布區域，給出修正后的針輪接觸應力的計算方法。孫章棟等[8]研究擺線針輪傳動的接觸熱彈流潤滑特性，得到擺線針輪副完整嚙合周期內摩擦力及摩擦損失功率變動。楊冰等[9]分析并測試擺線針輪行星減速器工作的振動和噪聲。何衛東[10]通過改變環板式針擺行星傳動的結構，以及對主、從齒的齒廓進行優化修緣來降低其振動，并進行了實驗研究。

上述擺線針輪行星減速器的振動研究，在建模和分析中都忽略一些非線性因素，研究不夠深入，有些工作缺乏試驗和工程數據。再結合現有擺線針輪行星減速器使用現狀，由于轉矩和轉速的波動、各零部件的制造誤差和裝配誤差、零部件的磨損等，導致擺線針輪行星減速器的傳動精度降低、傳動振動和噪聲迅速上升，甚至出現卡死的現象。因此，針對現有擺線針輪行星減速器存在的一些技術不足和研究忽略的影響因素，提出一種安裝減振襯墊的新型擺線針輪行星減速器，并綜合考慮嚙合副間的非線性因素影響，對新設計的擺線針輪行星減速器的振動進行研究，為后續擺線針輪行星減速器的動態設計、降噪提供理論依據和技術支持。

1 新型擺線針輪行星減速器傳動原理

新型擺線針輪行星減速器主要結構部件：偏心驅動輸入機構(部件7、12～16、19)、減振件(部件17和18)、擺線針輪嚙合機構(部件3～6、8和9)和輸出傳動機構(部件1、2、10、11、20和21)，結構原理圖如圖1所示。

圖1 新型擺線針輪行星減速器結構原理圖Fig.1 Structure schematic diagram of newpin-cycloid speed reducer

減振件是新型擺線針輪行星減速器減振降噪的關鍵傳動件，圖2示出了減振襯墊的安裝位置，主要用于減小、阻斷電機和傳動過程中產生的高頻波動，并向低頻段轉移，提高傳動精度。

圖2 減振襯墊安裝位置示意圖Fig.2 Installation diagram of damping mat

傳動原理：偏心激波套筒、偏心激波套筒軸承I和II相對于高速軸偏心安裝；偏心激波套筒軸承I和II運動相位相差180°；偏心激波套筒軸承I和II外圈分別裝有減振襯墊Ⅰ和Ⅱ；在減振襯墊I和II外圈上裝有相位相差180°的擺線外齒輪I和Ⅱ。高速軸轉動，帶動偏心激波套筒、偏心激波套筒軸承I和II轉動，帶動擺線外齒輪I和II以高速軸軸線為中心做公轉運動。擺線外齒輪Ⅰ和Ⅱ的外齒廓與滾動柱銷套筒相嚙合，滾動柱銷套筒的軸線由滾動柱銷所固定，故滾動柱銷套筒會對擺線外齒輪I和II產生與其公轉方向相反的力，推動擺線外齒輪Ⅰ和Ⅱ相對于高速軸以擺線外齒輪I和II的軸線為中心進行反向自轉，且推動高-低速連接柱銷套筒及高-低速鏈接柱銷以低速軸為中心相對于高速軸反向轉動，繼而帶動低速軸相對于高速軸做反向轉動，從而達到減速增矩的目的。

2 系統內部激勵

擺線輪傳動系統的動態激勵是產生噪聲和振動的根本原因，文中僅研究擺線輪與滾動柱銷套筒、擺線輪柱銷孔與高-低速連接柱銷套筒間嚙合時的內部激勵，包括時變剛度、制造安裝誤差以及嚙入沖擊激勵。

圖3為擺線輪傳動系統內部激勵計算流程圖，利用擺線輪與滾動柱銷套筒、擺線輪柱銷孔與高-低速連接柱銷套筒嚙合副嚙合接觸分析的結果，可準確進行內部激勵的計算。相關幾何接觸分析和承載接觸分析以及擺線輪與滾動柱銷套筒、擺線輪柱銷孔與高-低速連接柱銷套筒嚙合副嚙合接觸分析見嚙合分析文獻所述計算方法[3-5, 11-13]。

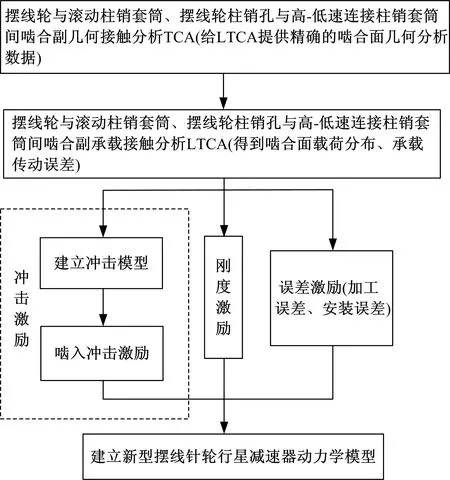
圖3 內部激勵計算流程圖Fig.3 Calculation flow chart of internal excitations

2.1 計算時變剛度激勵

要精確建立擺線輪與滾動柱銷套筒、擺線輪柱銷孔與高-低速連接柱銷套筒的嚙合剛度模型比較困難，文中采用分解擺線輪運動過程來模擬擺線輪的整個運動過程，利用擺線輪與滾動柱銷套筒、擺線輪柱銷孔與高-低速連接柱銷套筒嚙合副承載接觸分析得到不同嚙合位置的接觸力和接觸變形，從而得到該位置的嚙合剛度。擺線針輪行星減速器傳動比為29，故高速軸轉動一周，擺線輪旋轉約12.4°。在整個嚙合過程中，若某嚙合位置有多對擺線輪參與嚙合，那么該嚙合位置的嚙合綜合剛度是由在該位置同時參與嚙合的單對嚙合剛度疊加而成，將嚙合剛度的離散值通過多項式擬合和Fourier 級數變換展開成周期函數。

圖4為擺線輪與滾動柱銷套筒嚙合副兩個嚙合周期內的嚙合剛度變化趨勢和擬合曲線，綜合剛度值以約12°為周期變化，與理論計算周期12.4°基本一致。剛度最大值為2.4×108N/m，最小值為1.28×108N/m，差值接近1倍。圖5為擺線輪柱銷孔與高-低速連接柱銷套筒嚙合副兩個嚙合周期內的嚙合剛度變化趨勢和擬合曲線，綜合剛度值周期也與計算周期12.4°接近，最大值為1.74×108N/m，最小值為0.48×108N/m，差值約2.5倍。由于嚙合區域隨嚙入或嚙出呈現周期性變化，故綜合剛度的最大值和最小值相差較大，且具有周期性，是系統產生振動和噪聲的一個重要因素。

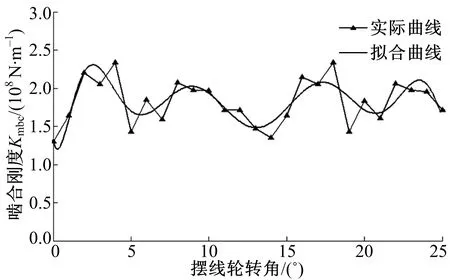
圖4 擺線輪與滾動柱銷套筒嚙合綜合剛度曲線圖Fig.4 Synthetical meshing stiffness curve ofcycloid gear with rolling pin-sleeve

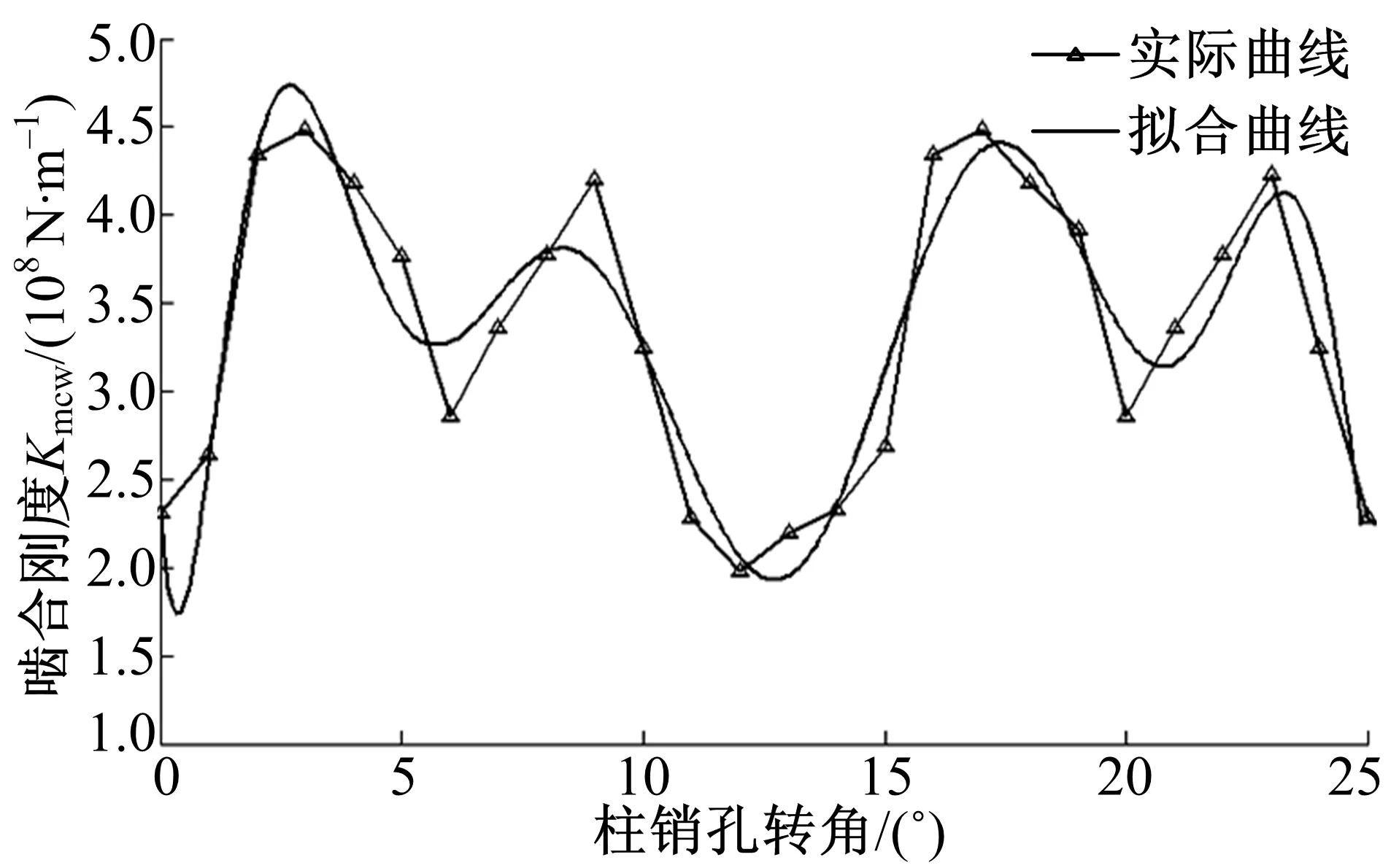
圖5 柱銷孔與高-低速連接柱銷套筒嚙合綜合剛度曲線圖Fig.5 Synthetical meshing stiffness curve of cylindricalpin hole with high-low speed connection pin-sleeve

2.2 計算傳動誤差激勵

研究中僅考慮擺線輪齒形誤差和基節誤差，根據擺線輪加工精度等級通過查手冊，合成系統等效誤差，再通過簡諧函數來模擬誤差。低轉速下，擺線輪制造安裝誤差引起的軸向位移也是擺線輪高速運動時振動的激勵源。根據擺線輪齒形誤差和基節誤差，利用擺線輪副承載接觸分析得到低轉速下長周期內的軸向位移，經Fourier 級數展開后其周期函數曲線見圖6。

圖6 軸向位移曲線Fig.6 Axial displacement

2.3 計算沖擊激勵

嚙合沖擊主要是由嚙入、嚙出和節點沖擊組成，三者對于擺線輪傳動性能的影響，嚙入沖擊最大，故本文僅考慮嚙入沖擊對系統的影響。最大嚙入沖擊力計算公式[14]：

(1)

式中：Δv是嚙入沖擊速度；J1、J2對應嚙合物體1和2的轉動慣量；rb1、rb2對應嚙合物體1和2的瞬時嚙合線對應的瞬時基圓半徑；b是擺線輪寬；qs是初始嚙入點處的綜合柔度。

將得到的嚙合點的沖擊力通過多項式擬合以及Fourier級數變換展開成周期函數。轉速1400 r/min時，一個嚙合周期內擺線輪與滾動柱銷套筒、擺線輪柱銷孔與高-低速連接柱銷套筒的嚙入沖擊力曲線見圖7。

圖7 嚙入沖擊力曲線圖Fig.7 Meshing impact

3 空間動力學模型

在實際工程中，擺線針輪行星減速器系統的傳動是非常復雜的，故基于以下假設建立振動模型：不考慮擺線針輪行星減速器傳動系統中各旋轉、滑動、嚙合接觸等部位的摩擦力影響；用等效彈簧剛度表示傳動系統中回轉副、嚙合副和支持軸承處所產生的彈性變形；減振襯墊I和II的物理和幾何參數一致，擺線輪I和II的物理和幾何參數一致。

應用集中參數法建立新型擺線針輪行星減速器系統的非線性振動模型，圖8是簡化后的振動模型，建立的振動系統包含8個自由度：

{δ}={yH，θH，yb,θb,yc，θc，yw，θw}

(2)

式中：yi、θi表示高速軸H、滾動柱銷套筒b、擺線輪c、低速軸w的垂直振動位移和扭轉振動位移，i=H,b,c,w。

圖8 傳動系統的非線性振動模型Fig.8 Nonlinear vibration model of transmission system

需將減振襯墊的影響考慮到系統內部各部件的振動微分方程中，得到垂直和扭轉方向的振動微分方程：

(3)

(4)

(5)

(6)

式中：mi、Ii分別為高速軸H、滾動柱銷套筒b、擺線輪c、低速軸w的質量和轉動慣量，i=H,b,c,w；Ci、Ki分別為支撐等效元件模型的阻尼和剛度，i=H,b,w；Cθ、Kθ分別為高速軸扭轉阻尼和扭轉剛度；Cr、Kr分別為減振襯墊徑向阻尼和剛度；Ca、Ka分別為減振襯墊扭轉阻尼和剛度；Cmbc、Kmbc分別為擺線輪與滾動柱銷套筒嚙合阻尼和時變嚙合剛度；Cmcw、Kmcw分別為擺線輪柱銷孔與高-低速連接柱銷套筒嚙合阻尼和時變嚙合剛度；fi(yi)為間隙型非線性力-位移函數，i=H,b,w；TH、Tw為輸入轉矩和輸出轉矩；rc為擺線輪分度圓半徑；Rw為柱銷孔中心圓半徑；rp為滾動柱銷中心圓半徑；ebc、ecw為靜態傳遞誤差；Δybc、Δycw為動態傳遞誤差。

嚙合線上的相對位移：

(7)

各嚙合副法向阻尼均由下式求得：

(8)

式中：ζv為各嚙合副對應的相對嚙合阻尼系數，計算中取0.065；K為各嚙合副對應的平均嚙合剛度；m為各嚙合副對應的等效質量。

當yi>3bi(振動間隙)，間隙型非線性力-位移函數的非線性程度并不明顯，近似轉化為分段線性函數：

(9)

4 動力學模型的求解與分析

表1為新型擺線針輪行星減速器的等效機構參數，利用仿真擺線輪與滾動柱銷套筒、擺線輪柱銷孔與高-低速連接柱銷套筒嚙合特性的結果，得到上述嚙合綜合剛度圖4和圖5，以及低轉速下擺線輪的軸向位移圖6和嚙合沖擊激勵圖7。采用變步長四階Runge-Kutta對降階后的振動微分方程組求解，對比剛性與非剛性結構下的擺線輪、低速軸的垂直振動和扭轉振動。

4.1 垂直振動對比

圖9為傳動系統達到工作穩態時擺線輪的垂直振動位移。圖9(a)中振動平衡點位置維持在-10 μm，且在0.01 s后趨于穩定，幅值約為2.8 μm。圖9(b)中振動平衡時間約0.07 s，振動平衡點位置維持在-7 μm，幅值約1.5 μm。非剛性系統下的擺線輪的平衡振動位移值比剛性振動模型的對應值降低約3 μm，振動幅值減小。

表1 等效機構參數Table 1 Equivalent mechanism parameters

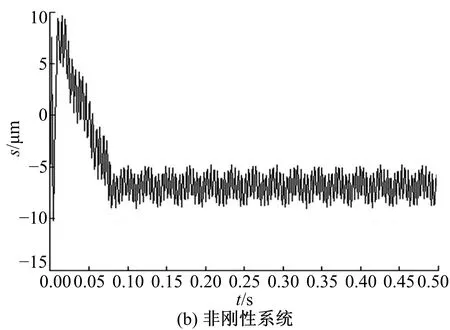
圖9 擺線輪垂直振動位移Fig.9 Vertical vibration displacement of cycloid gear

圖10為低速軸垂直振動位移。圖10(a)低速軸經小幅振動后達到振動平衡時間約為0.05 s，平衡點位置在9.2 μm，振動幅值約為0.6 μm。圖10(b)振動平衡時間約為0.06 s，振動平衡點位置在7.5 μm，振動幅值約為0.5 μm。非剛性系統下的低速軸的平衡點振動位移值比剛性振動模型的對應值降低約1.7 μm，振動幅值降低約0.3 μm 。圖9、圖10的結果表明，在新型擺線針輪行星減速器中添加減振襯墊后，擺線輪和低速軸的垂直振動平衡點位移值和振動幅值都減小，在垂直方向起到減振的效果。

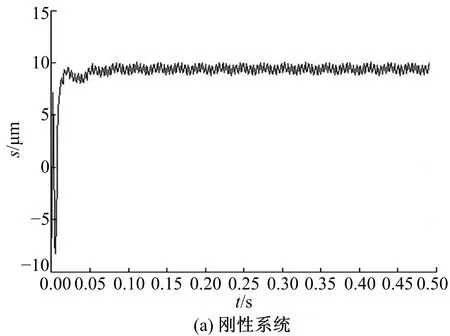
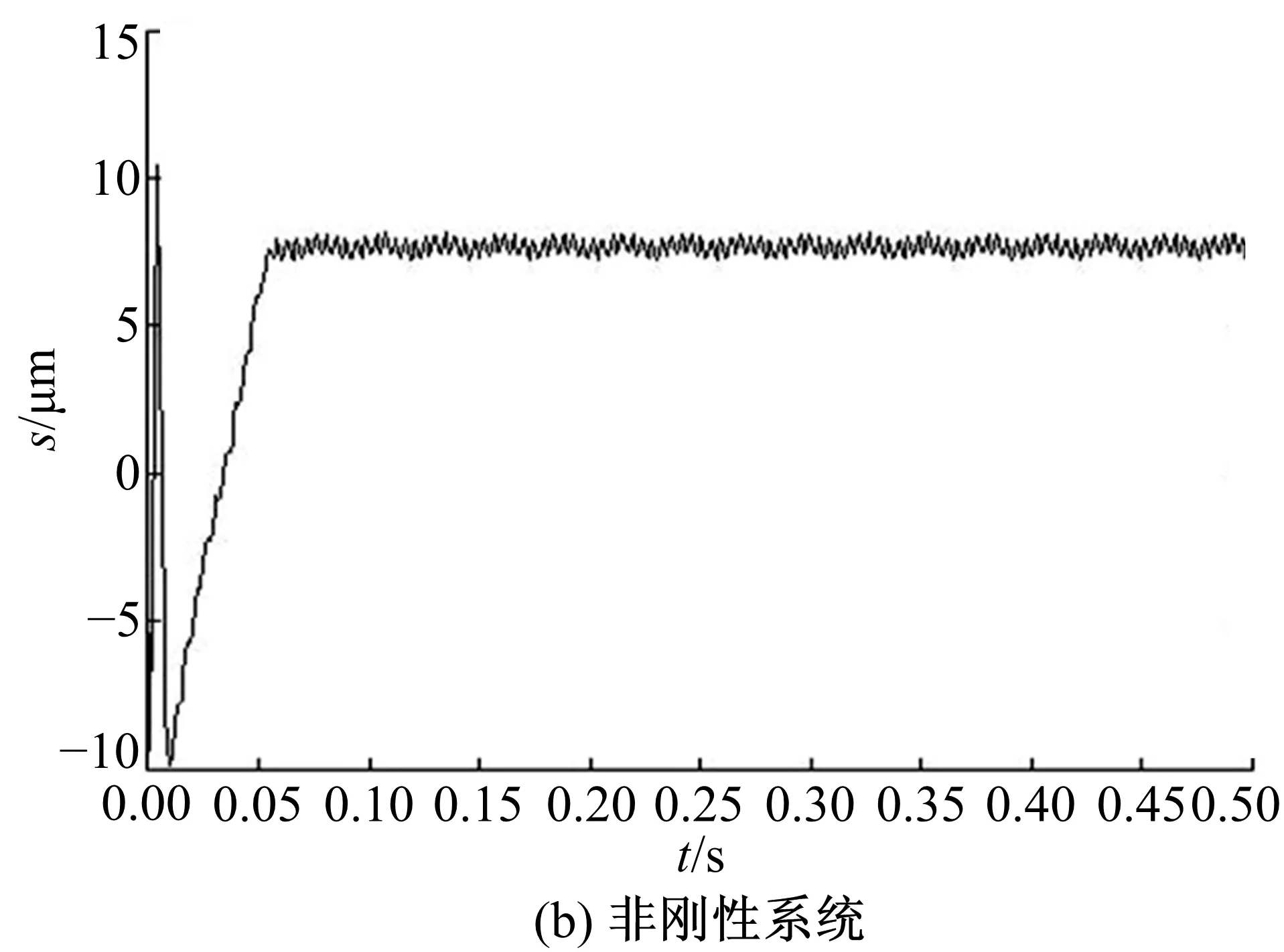
圖10 低速軸垂直振動位移Fig.10 Vertical vibration displacement of low speed shaft

圖11為傳動系統達到工作穩態時擺線輪的垂直振動速度。圖11(a)中速度振動幅值約為5.8 mm/s，圖11(b)中速度振動幅值約為4 mm/s。圖12為穩態時低速軸的垂直振動速度，圖12(a)中幅值約為1 mm/s，圖12(b)中幅值約為0.8 mm/s。圖11、圖12數據表明，新型減速器的擺線輪和低速軸的振動速度幅值均比剛性減速器的對應值小，減振襯墊使垂直方向的振動程度降低。圖13和圖14是剛性與非剛性結構下的擺線輪和低速軸的垂直振動位移-速度相圖，二者相圖為近似環形閉合曲面和不規則橢圓閉合曲面相互往復重疊由內向外交叉循環擴展，表明擺線輪和低速軸呈現穩態響應的近混沌狀態。此外，相圖中表明非剛性結構下的擺線輪和低速軸的垂直振動位移-速度相圖曲線比剛性情況的更具有規律性。圖15和圖16是對應圖13和圖14的擺線輪和低速軸垂直振動位移-速度Poincaré截面，圖中顯示各個截面均為成片分布的密集點，且每個點都可以在各自相圖曲線上一一對應。密集點存在一定方向性，但Poincaré截面的規律性并不強，說明剛性與非剛性結構下的擺線針輪和低速軸處于穩態響應的近混沌狀態，與各相圖分析結果一致。

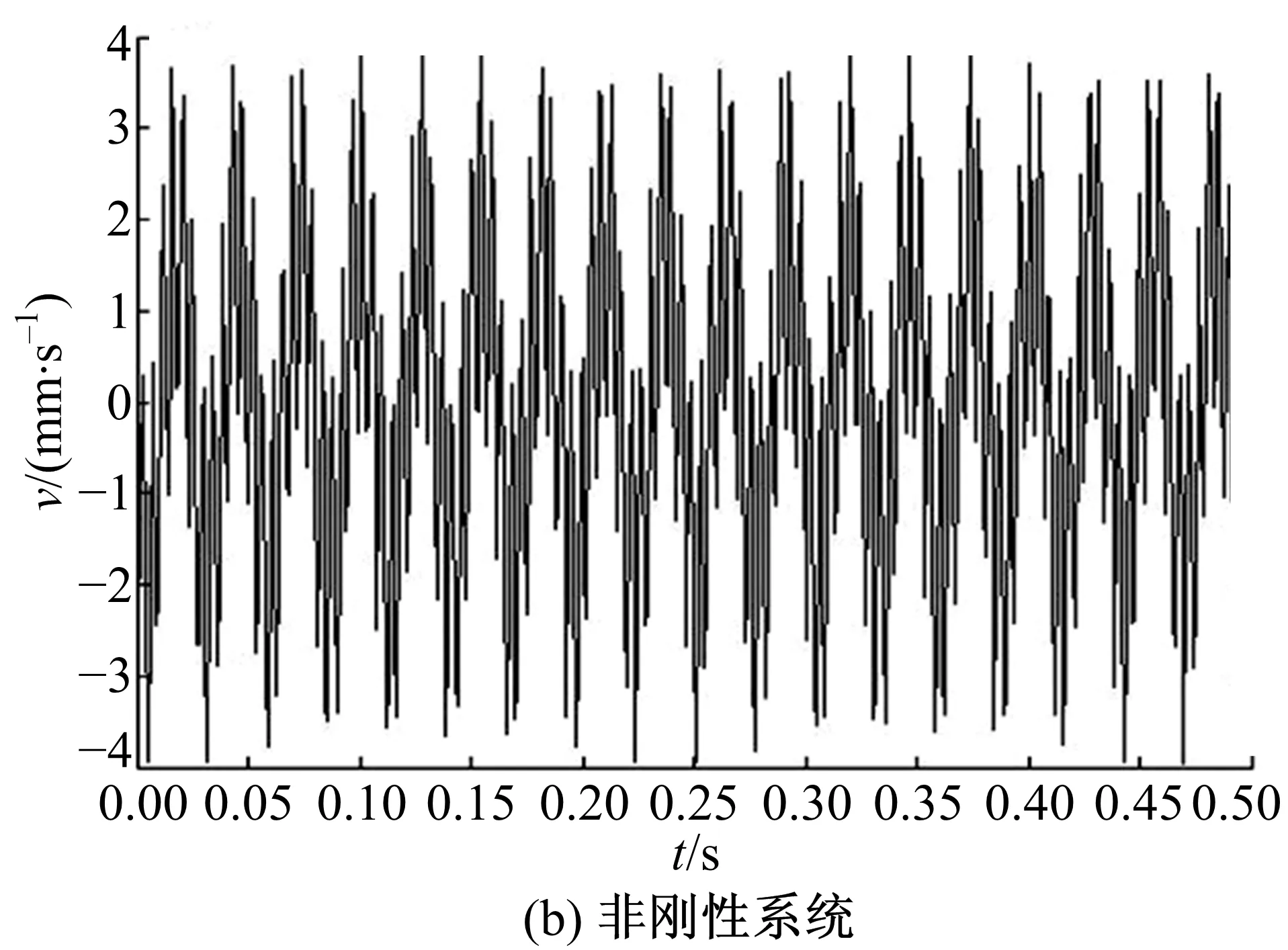
圖11 擺線輪垂直振動速度Fig.11 Vertical vibration velocity of cycloid gear

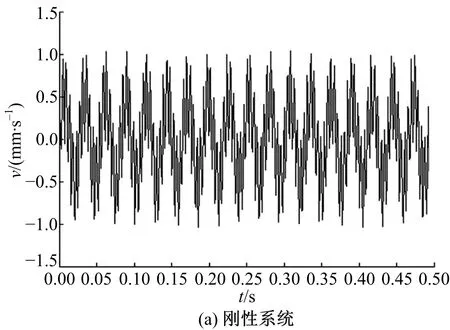
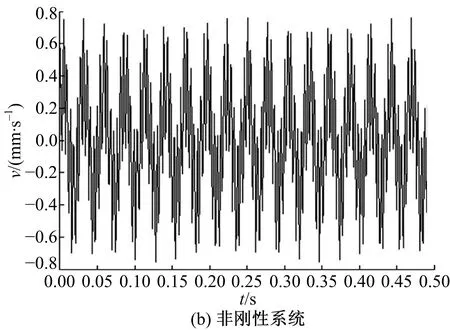
圖12 低速軸垂直振動速度Fig.12 Vertical vibration velocity of low speed shaft

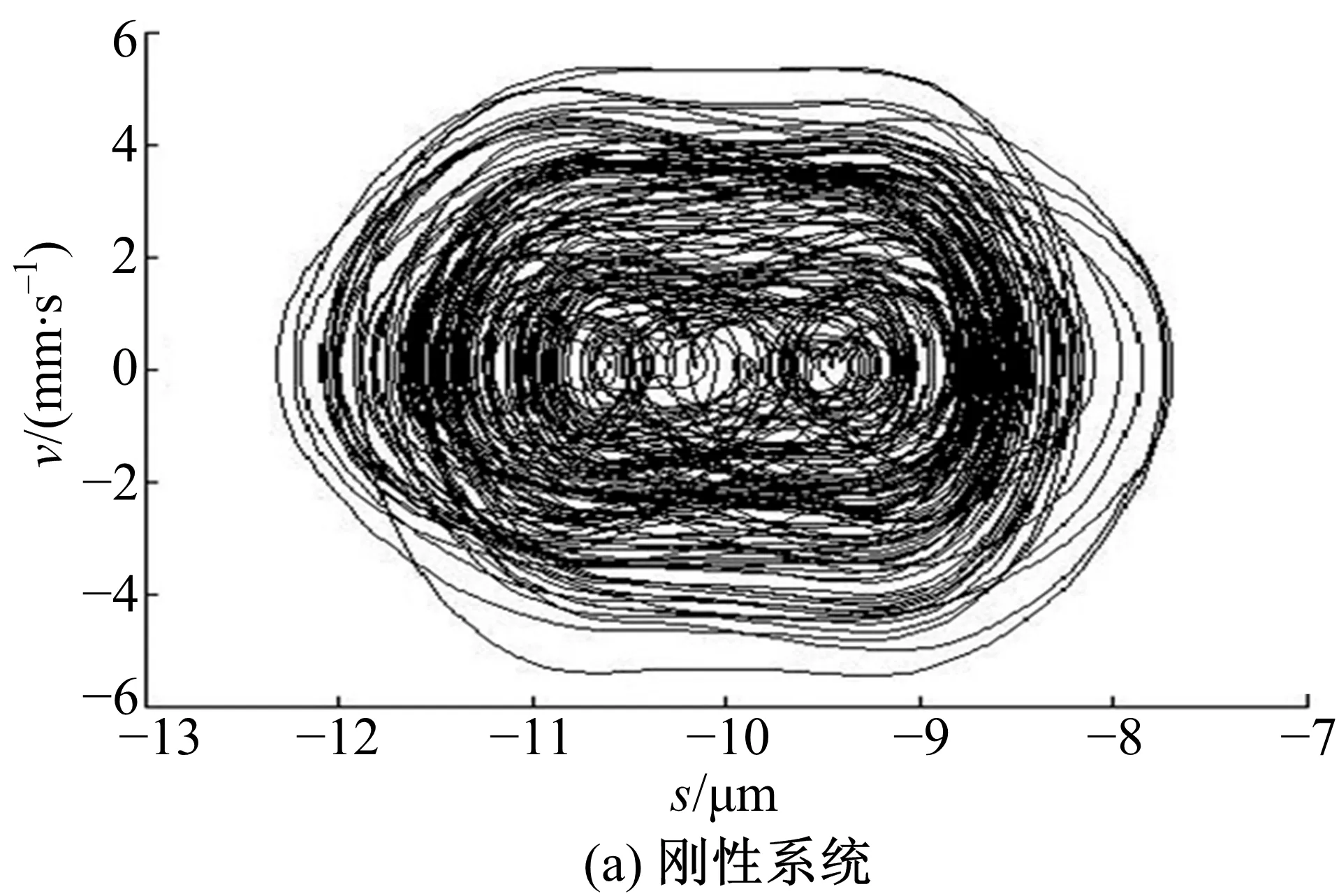
圖13 擺線輪垂直振動位移-速度相圖Fig.13 Vertical vibration displacement-velocityphase of cycloid gear

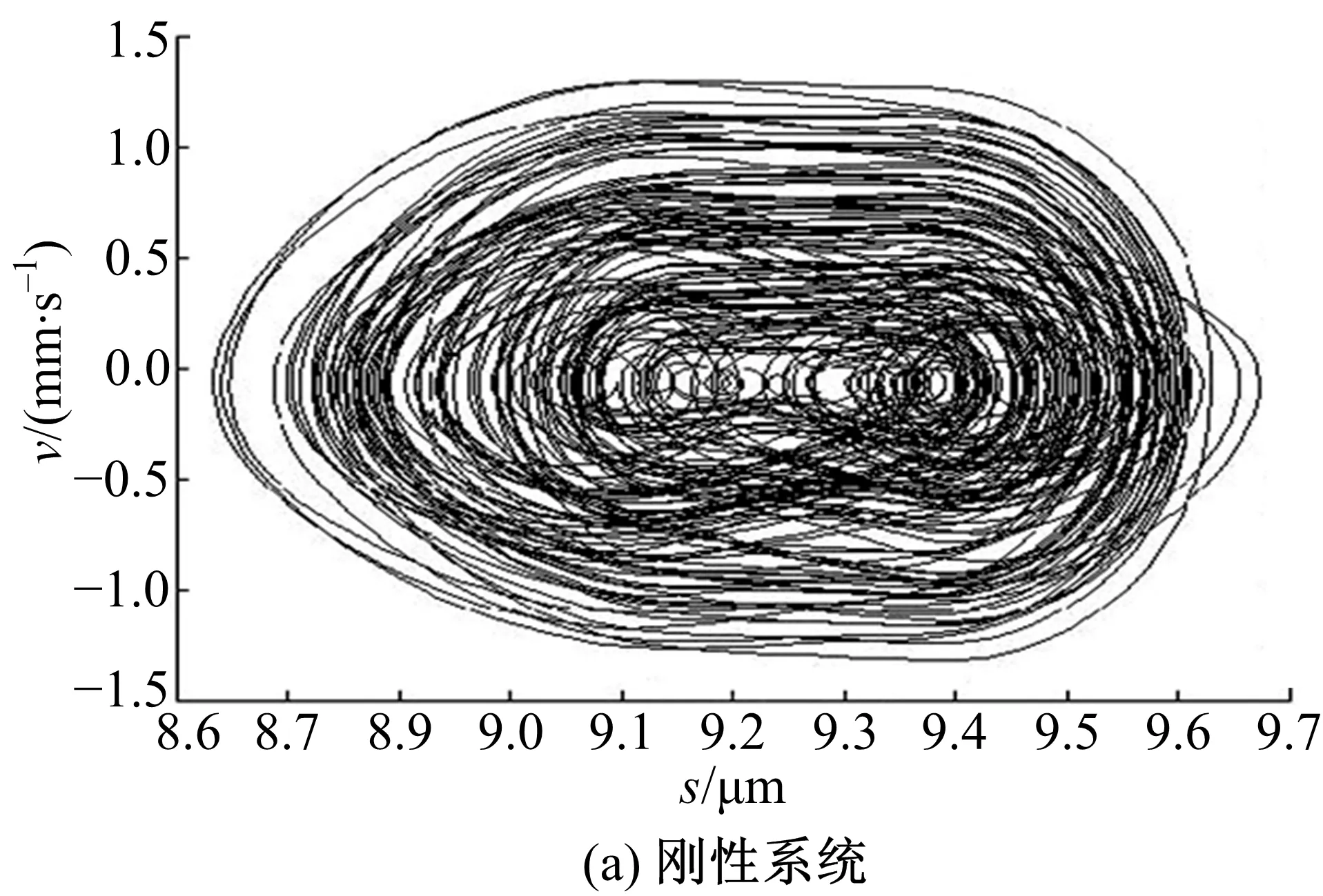
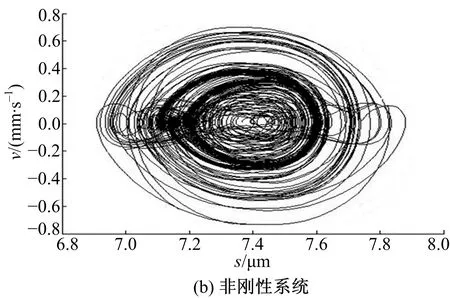
圖14 低速軸垂直振動位移-速度相圖Fig.14 Vertical vibration displacement-velocityphase of low speed shaft

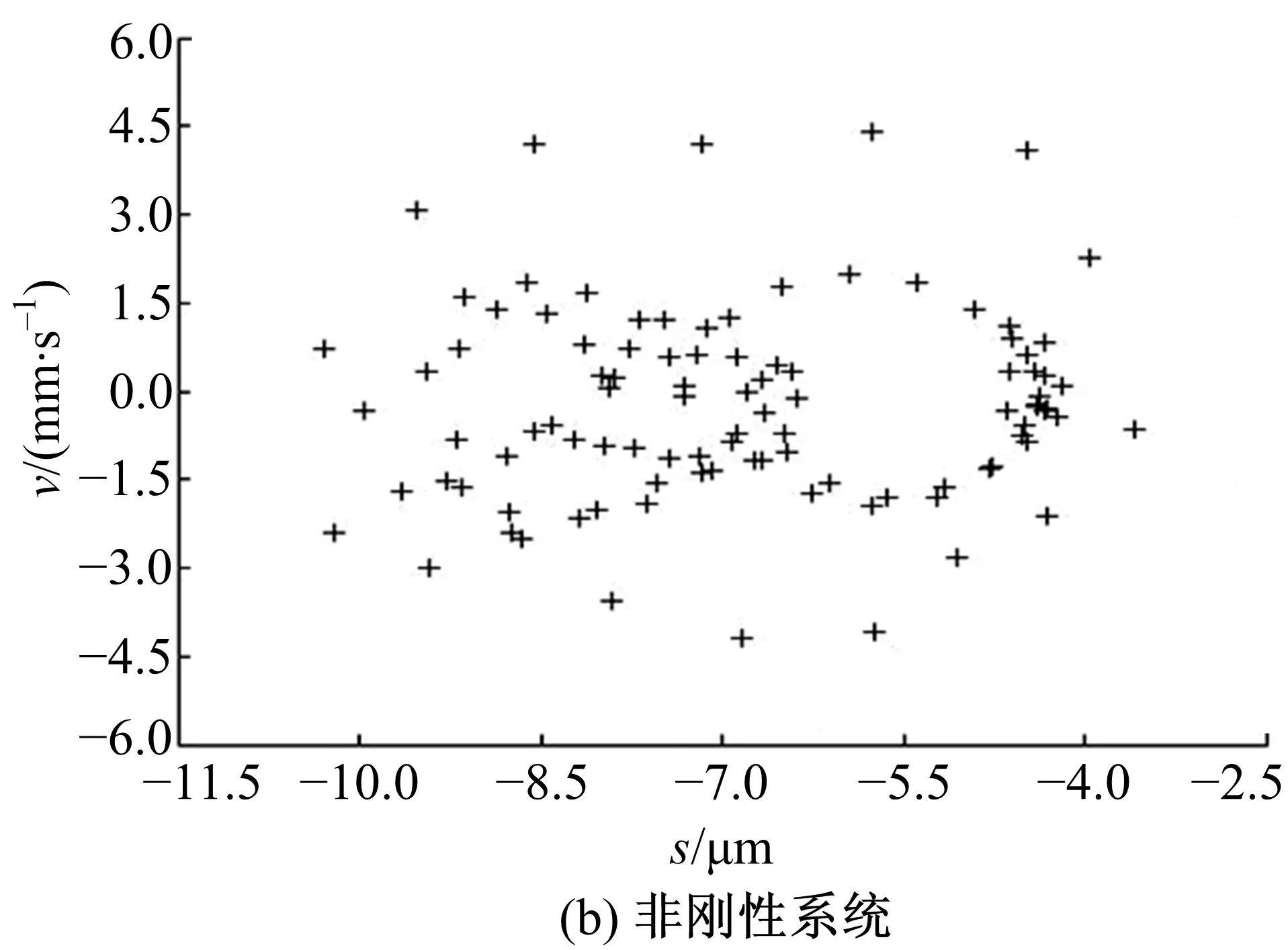
圖15 擺線輪垂直振動位移&速度Poincaré截面Fig.15 Vertical vibration displacement-velocityPoincaré section of cycloid gear

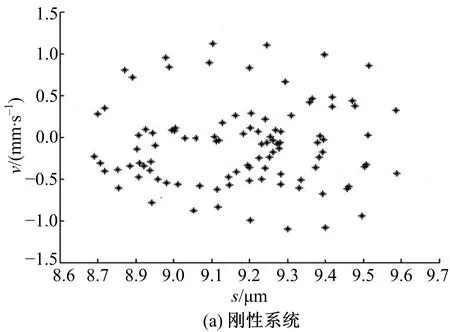
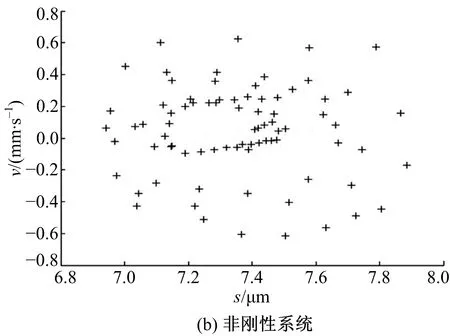
圖16 低速軸垂直振動位移-速度Poincaré截面Fig.16 Vertical vibration displacement-velocityPoincaré section of low speed shaft

4.2 扭轉振動對比

圖17為傳動系統工作穩態時擺線輪的扭轉振動角位移。圖17(a)中振動平衡點位置維持在0.02°，幅值約0.03°。圖17(b)中平衡點位置維持在0.028°，振動幅值約0.013°。對比兩種情況下的擺線輪扭轉振動，都很快達到振動平衡，圖17(b)中振動平衡點偏離角值比圖17(a)的對應值將近大0.01°，但振動幅值要小0.017°。說明新型擺線針輪行星減速器中添加減振襯墊后，由于減振襯墊的變形導致擺線輪的扭轉振動平衡點位置變大，同時對內部的振動起到緩沖，使振動幅值減小。

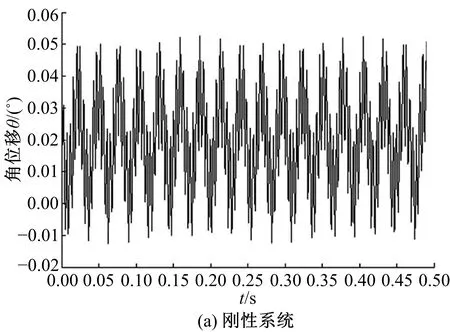
圖17 擺線輪扭轉振動角位移Fig.17 Torsional vibration angular of cycloid gear

圖18為傳動系統工作穩態時低速軸的扭轉振動角位移。圖18(a)中低速軸振動平衡點位置維持在-0.2°，幅值約0.3°。圖18(b)中振動平衡點位置維持在-0.1°，振動幅值約0.23°。對比兩種情況下的低速軸扭轉振動，都很快達到振動平衡，圖18(b)中低速軸的振動平衡點偏離角值比圖18(a)中的值小0.1°，振動幅值減小約0.07°。說明新型擺線針輪行星減速器中添加減振襯墊后，使低速軸的振動角位移和振動幅值都減小。

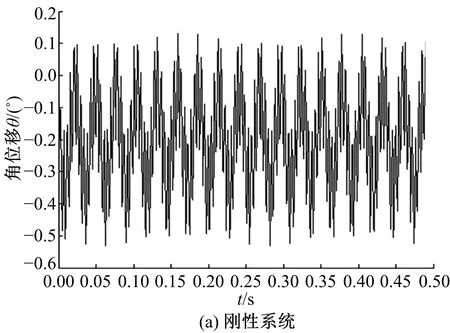
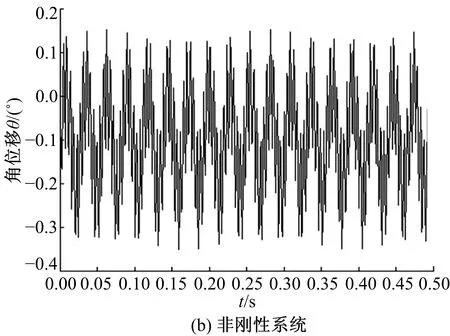
圖18 低速軸扭轉振動角位移Fig.18 Torsional vibration angular of low speed shaft

圖19為傳統系統工作穩態時擺線輪的扭轉振動角速度，圖19(a)中振動幅值約為70 °/s，圖19(b)中振動幅值約為50 °/s。圖20為工作穩態時低速軸的扭轉振動角速度，20(a)中振動幅值約為150 °/s，20(b)中振動幅值約為120 °/s。圖19和圖20的數據表明，新型減速器的擺線輪和低速軸振動角速度的幅值小于剛性結構下的對應值，說明減振襯墊在擺線輪和低速軸扭轉方向起到減振作用。

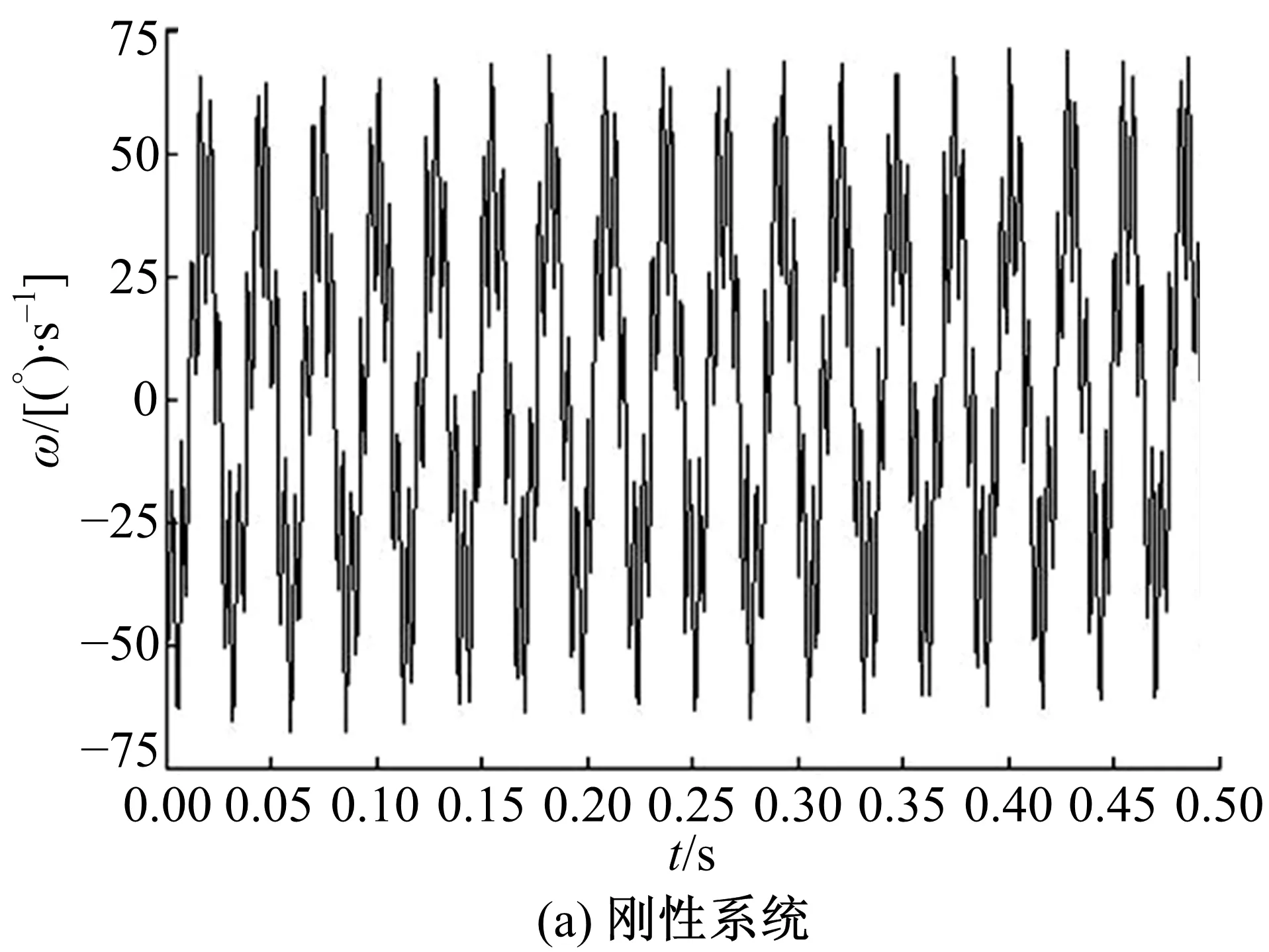
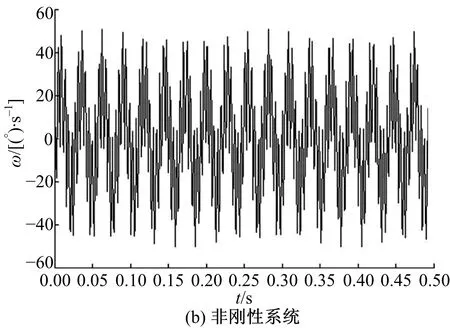
圖19 擺線輪扭轉振動角速度Fig.19 Torsional vibration angular velocity of cycloid gear

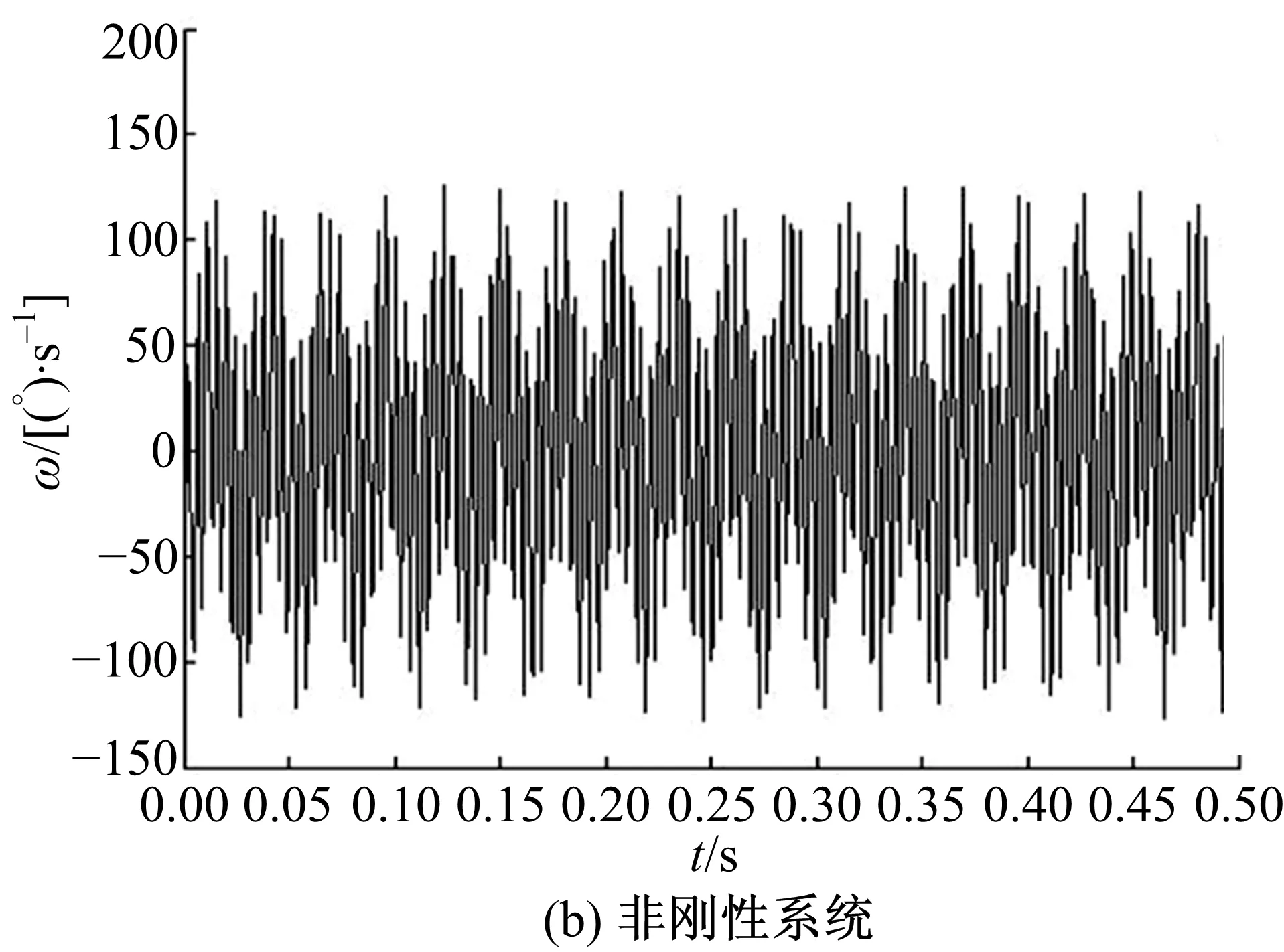
圖20 低速軸扭轉振動角速度Fig.20 Torsional angular velocity of low speed shaft

圖21和圖22是剛性與非剛性結構下的擺線輪和低速軸的扭轉振動角位移-角速度相圖，表明擺線輪和低速軸呈現穩態響應的近混沌狀態，這一點與前述垂直振動情況相同。圖23和圖24是對應圖21和圖22的擺線輪和低速軸扭轉振動角位移-角速度Poincaré截面，圖中顯示各個截面均為成片分布的密集點，且每個點都可以在各自相圖曲線上一一對應。密集點存在一定方向性，但Poincaré截面的規律性并不強，說明剛性與非剛性結構下的擺線針輪和低速軸處于穩態響應的近混沌狀態，與各相圖分析結果一致。對比垂直振動和扭轉振動的相圖與Poincaré截面，扭轉振動的規律性比垂直振動情況好。

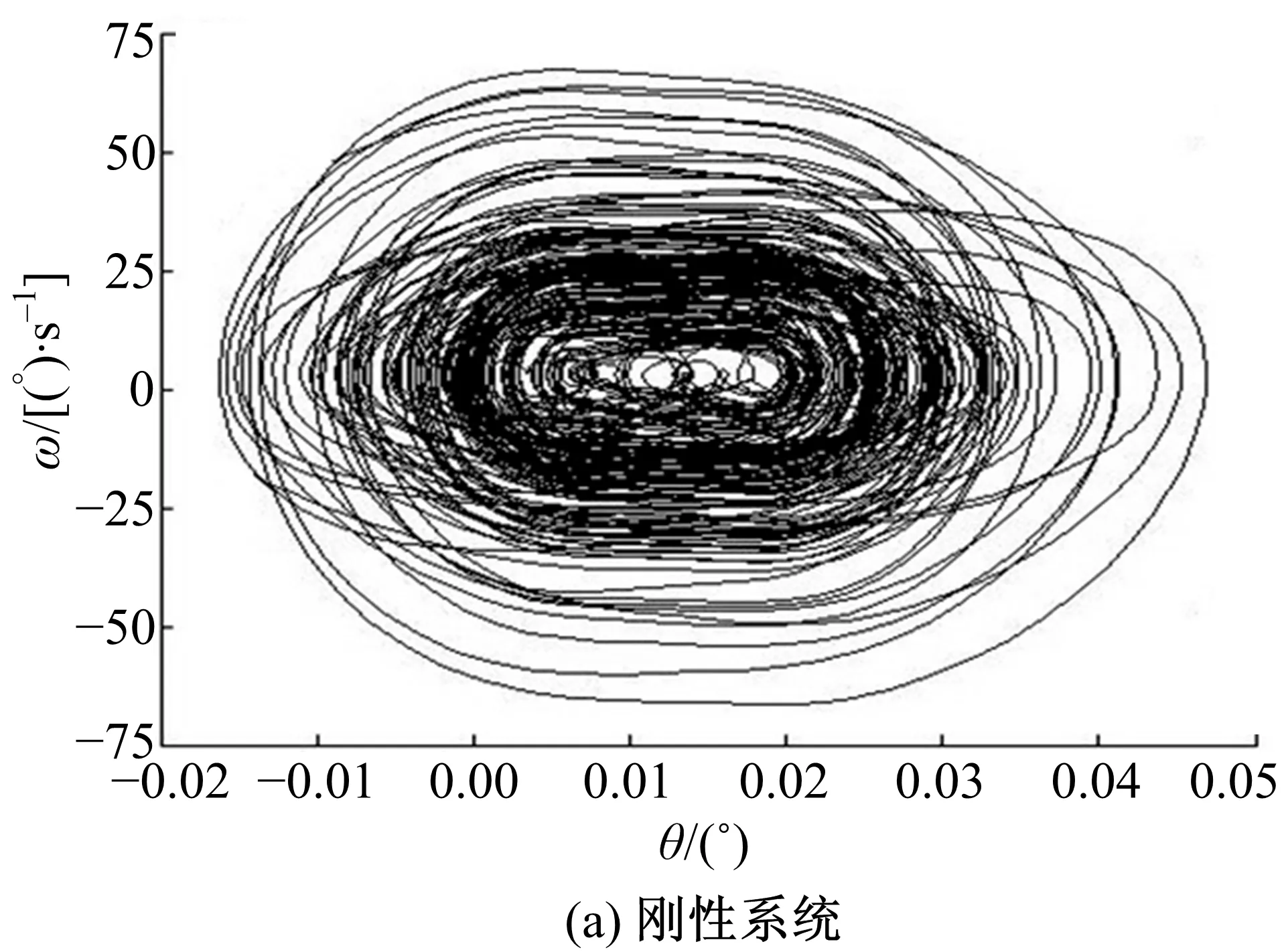
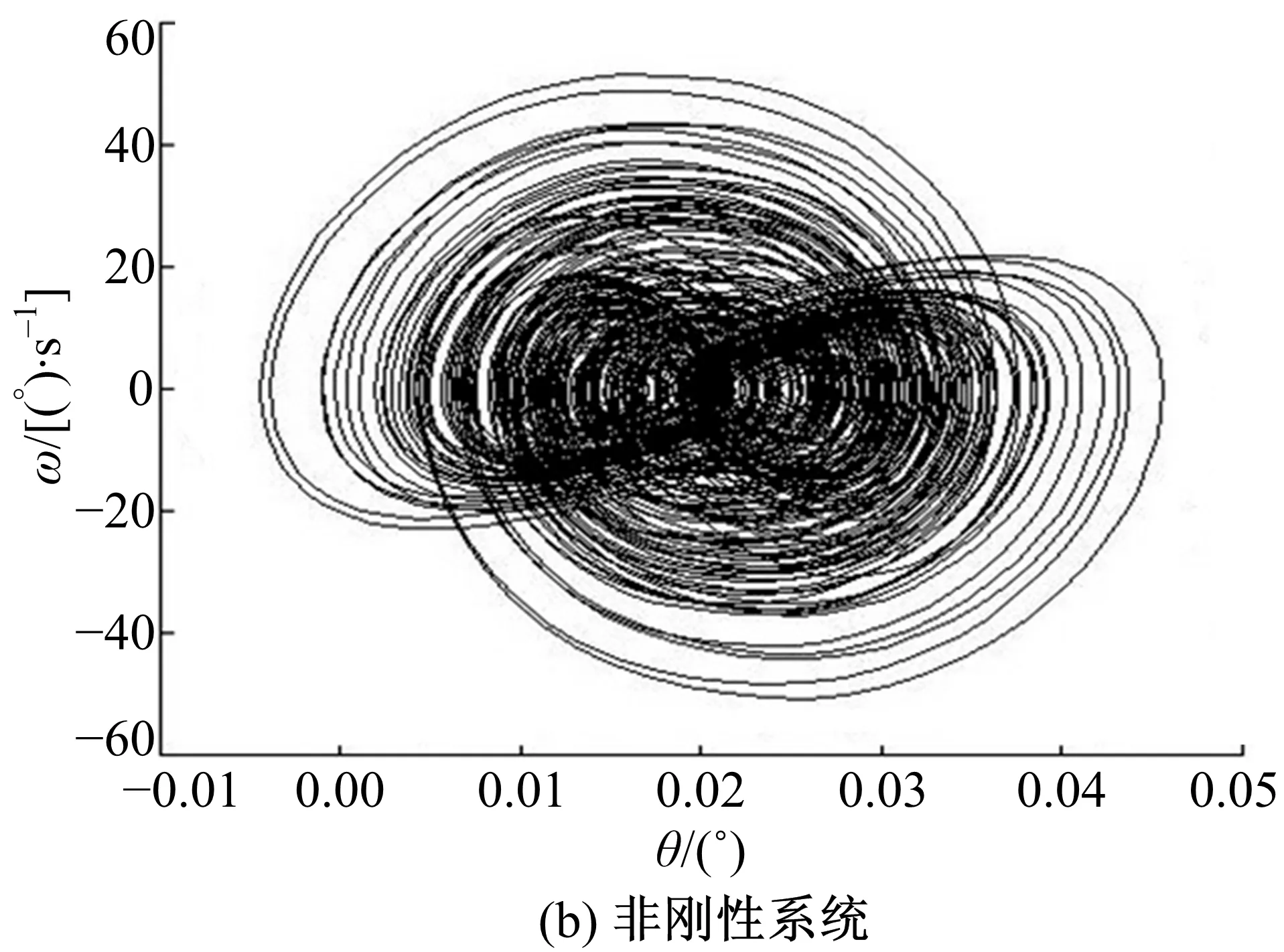
圖21 擺線輪扭轉振動角位移-角速度相圖Fig.21 Torsional vibration angular-angularvelocity phase of cycloid gear

圖22 低速軸扭轉振動角位移-角速度相圖Fig.22 Torsional vibration angular-angularvelocity phase of low speed shaft

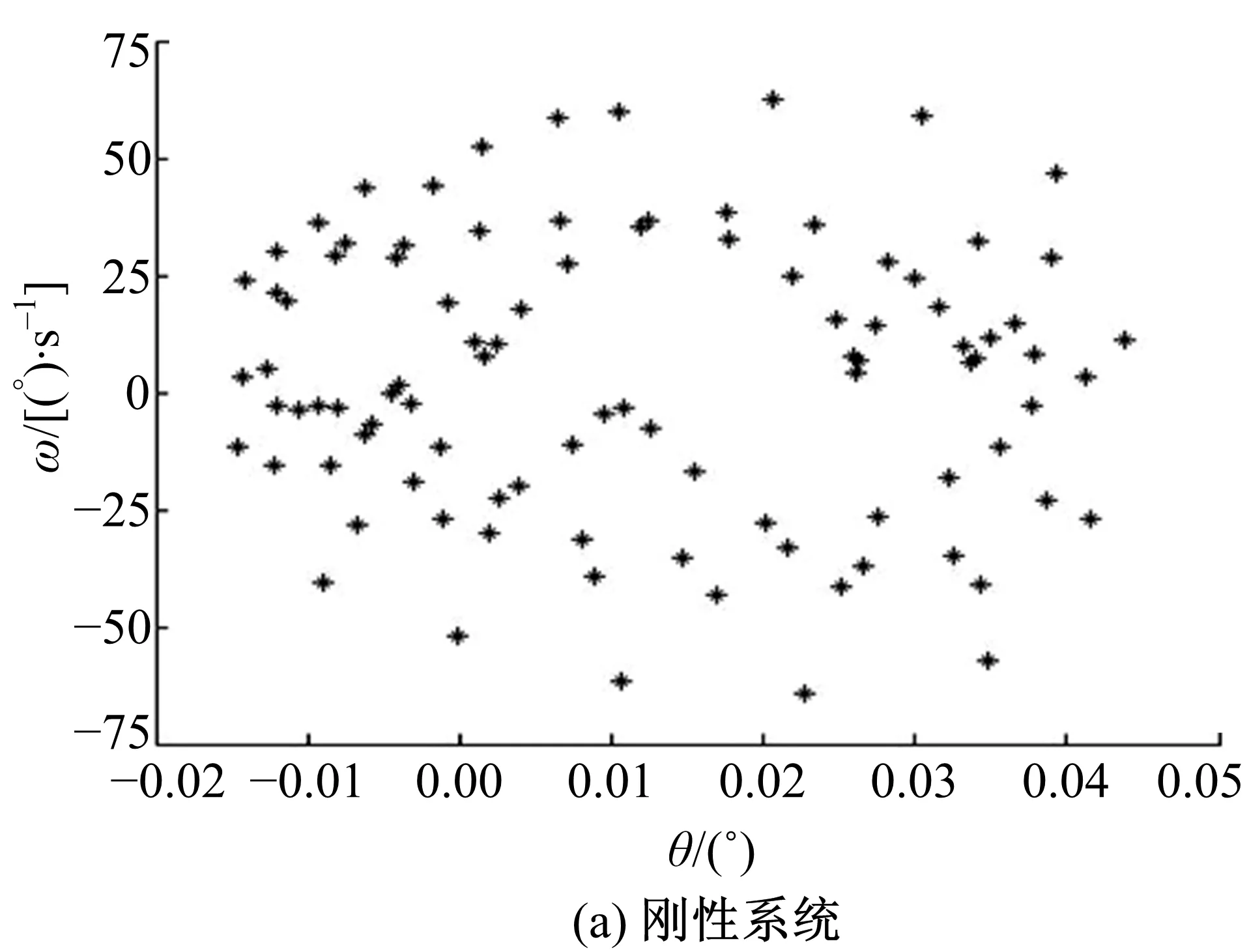
圖23 擺線輪扭轉振動角位移-角速度Poincaré截面Fig.23 Torsional vibration angular-angular velocityPoincaré section of cycloid gear

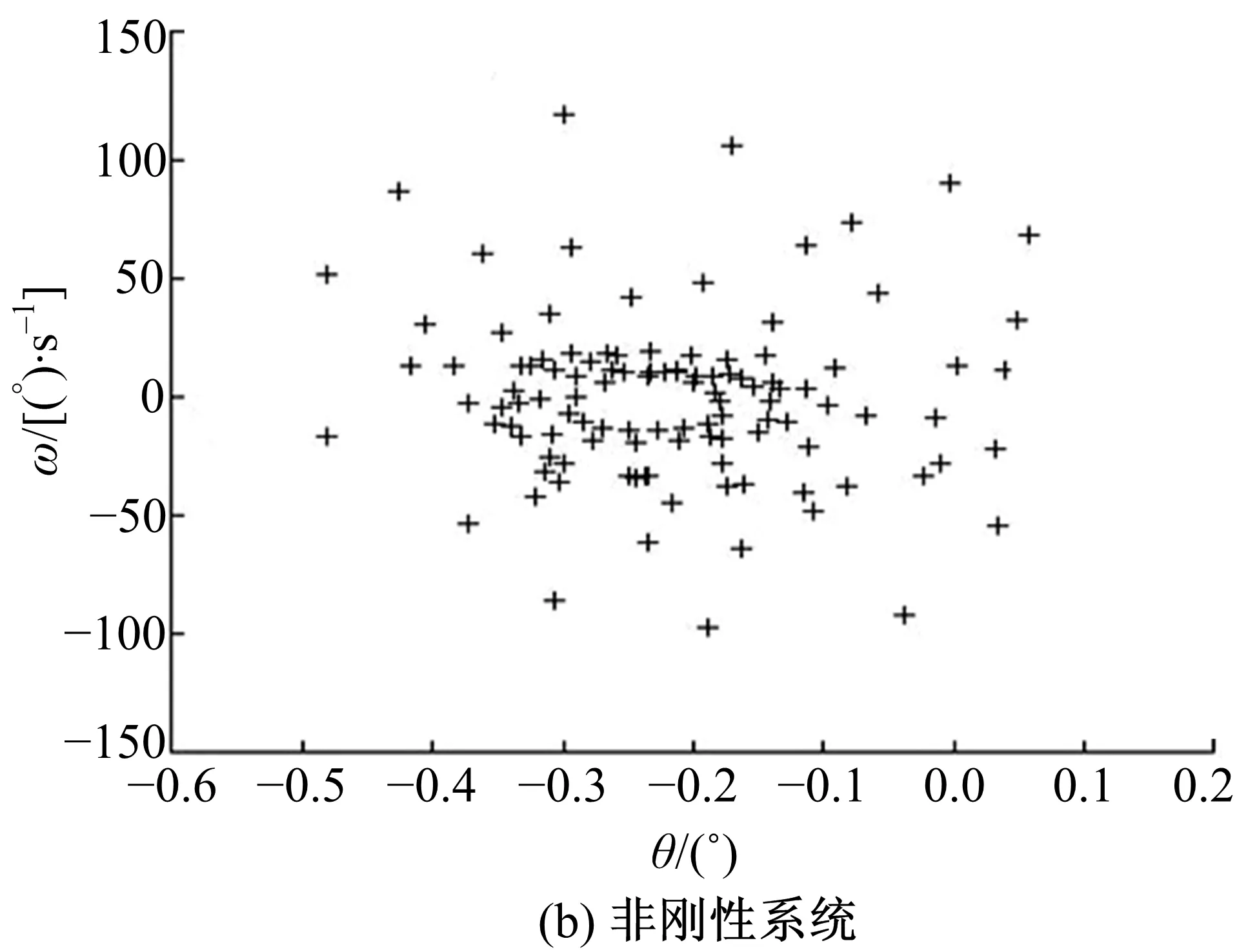
圖24 低速軸扭轉振動角位移-角速度Poincaré截面Fig.24 Torsional vibration angular-angular velocityPoincaré section of low speed shaft

5 振動測試

依據《GB8543-1987》對新型擺線針輪行星減速器的擺線輪和低速軸二者的表面進行振動測試，采用加速度傳感器獲取加速度振動信號，通過信號采集處理分析儀對采集的數據進行記錄和分析處理。

實驗主要設備：INV3020C型高精度信號采集處理儀、INV9832 ICP三向加速度傳感器、INV1841電荷調理儀等設備以及DASP V10數據采集與信號處理軟件。實驗中主要分析新型擺線針輪行星減速器的擺線輪和低速軸的垂直方向振動，并與傳統擺線針輪行星減速器的相關測試值進行比較，傳感器布置點如圖25所示。

圖25 傳感器布置Fig.25 Sensor sites

表2為輸入轉速分別為500、1000、1500 r/min三種工況下測試點處振動加速度的測試值，實驗中對每處測試點的振動加速度測取3次后求平均值，作為測試值。

結果表明：理論研究中的3種不同轉速工況下擺線輪垂直振動加速度峰值頻率分別出現在826.2、1392.4 和1832.7 Hz，與實驗測得的擺線輪垂直振動加速度值出現的峰值頻率821.4、1382.3和1824.5 Hz比較接近；不同轉速下低速軸垂直振動加速度峰值頻率分別出現在51.3、114.6和162.5 Hz，與實驗測得的低速軸垂直振動加速度值出現的峰值頻率46.6、107.4和153.4 Hz也比較接近。同時可以看到，擺線輪垂直振動加速度峰值0.8527、1.4622和1.9337 m/s2也接近實驗測得的峰值0.8251、1.2236和1.6854 m/s2；低速軸垂直振動加速度峰值0.2566、0.3725和0.6113 m/s2與實驗測得的峰值0.2225、0.3426和0.5817 m/s2也比較接近。此外，與傳統擺線針輪行星減速器對應工況下的擺線輪垂直振動加速度測試值0.7833、1.0832和1.5894 m/s2，以及對應的低速軸垂直振動加速度測試值0.2055、0.2988和0.4727 m/s2相比較，二者的測試值和幅值均降低。以上動力學分析表明：新型擺線針輪行星減速器的振動理論分析結果與實驗所測數據結果比較吻合，達到了預期研究目標。

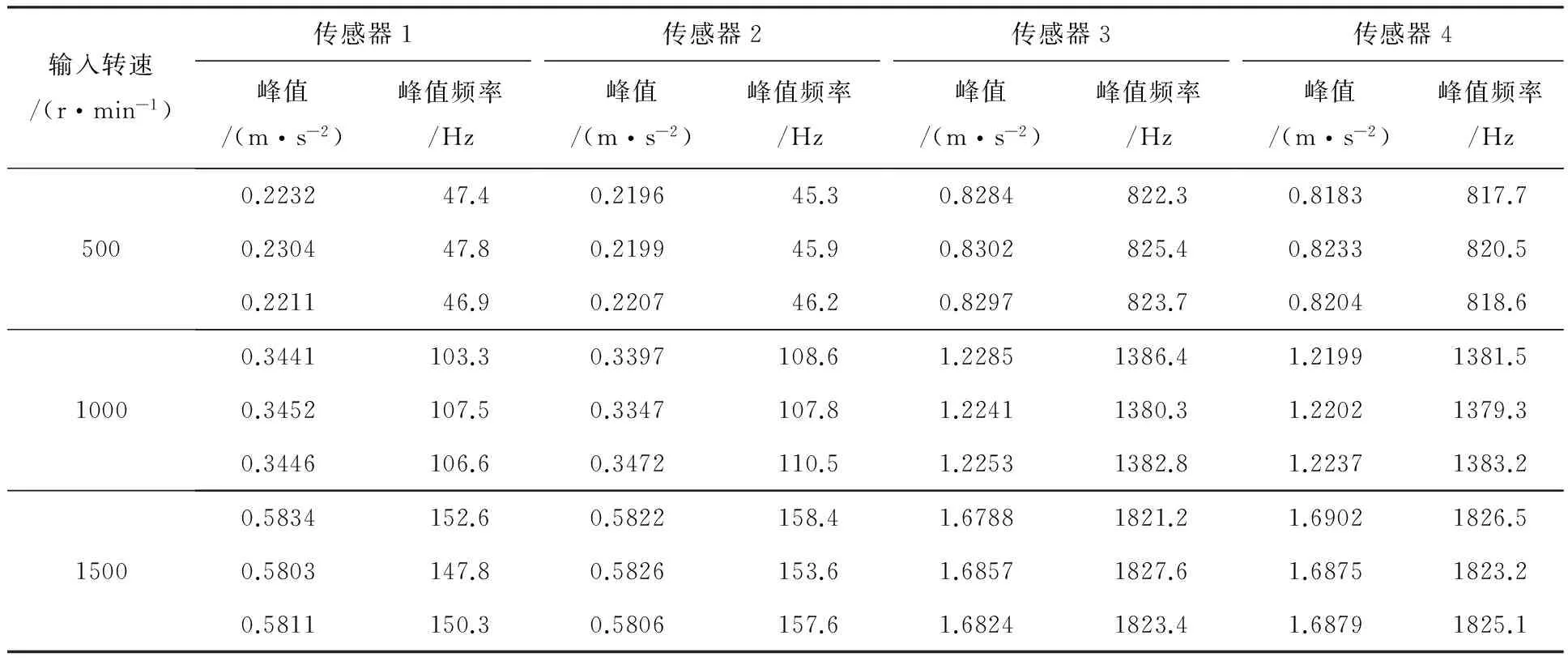
表2 實驗測試值Table 2 Test data

6 結 論

(1)以降低剛性擺線針輪行星減速器工作時的振動和提高其可靠性為主要研究目標，提出了一種安裝減振襯墊的新型擺線針輪行星減速器，并基于集中參數理論和牛頓第二定律建立其8自由度的多因素耦合動力學方程，對剛性與非剛性結構下的擺線輪和低速軸的垂直振動和扭轉振動進行仿真與實驗比較分析。

(2)基于文中建立的振動模型進行仿真實驗，仿真數據表明：采用減振襯墊，擺線輪和低速軸的垂直振動和扭轉振動變化更加平穩，為后續動態設計提供了理論依據。

(3)完成新型擺線針輪行星減速器樣機實驗測試，實驗結果與文中理論分析結果符合較好，驗證了新型擺線針輪行星減速器工作時的振動特性比剛性結構的系統要好，說明文中提出的安裝減振襯墊具有可行性，為其減振降噪提供了一種結構設計方案。

(4)研究中忽略了摩擦、回轉零件的偏心質量、箱體的變形等因素，在后續建立更加精確的動力學模型中應考慮這些參數的影響。

[1] Chen Bing-kui, Fang Ting-ting, Li Chao-yang. Gear geometry of cycloid drives [J]. Science in China Series E: Technological Sciences, 2008, 51(5): 598-610.

[2] Xu Li-xin, Yang Yu-hu. Dynamic modeling and contact analysis of a cycloid-pin gear mechanism with a turning arm cylindrical roller bearing [J]. Mechanism and Machine Theory, 2016, 104: 327-349.

[3] Li S. Design and strength analysis methods of the trochoidal gear reducers [J]. Mechanism and Machine Theory, 2014, 81: 140-154.

[4] Hsieh Chiu Fan. Traditional versus improved designs for cycloidal speed reducers with a small tooth difference: the effect on dynamics [J]. Mechanism and Machine Theory, 2015, 86: 15-35.

[5] Song Yuan, Liao Qi-zheng. Modelling, simulation and experiment of a novel pure rolling cycloid reducer with involute teeth [J]. International Journal of Modelling, Identification and Control, 2014, 21(2): 184-192.

[6] 李俊陽，王家序. 漸開線少齒差行星傳動的變形協調設計[J]. 中國機械工程，2014，25(5)：576-580.

Li Jun-yang, Wang Jia-xu. Deformation and compatibility design of involute planetary gear drive with small teeth difference [J]. China Mechanical Engineering, 2014, 25(5): 576-580.

[7] Sun Ying-shi, Guan Tian-min, Zhang Xu. Dynamic simulation of cycloid wheel at two support points of needle gear pin for new three-gear pin-cycloid driven speed reducer [J]. Advanced Materials Research, 2011, 291: 1195-1199.

[8]孫章棟，朱才朝，劉懷舉. 擺線針輪傳動接觸熱彈流潤滑特性[J]. 振動與沖擊，2016，35(6)：174-180.

Sun Zhang-dong, Zhu Cai-chao, Liu Huai-ju. TEHL characteristics of a cycloid drive [J]. Journal of Vibration and Shock, 2016, 35(6): 174-180.

[9] 楊冰，劉巖. 雙曲柄四環板式針擺行星減速器減振降噪研究[J]. 兵工學報，2011，32(10)：1282-1286.

Yang Bing, Liu Yan. Vibration and noise reduction of a double crank four ring-plate-type cycloid speed reducer [J]. Acta Armamentarii, 2011, 32(10): 1282-1286.

[10] 何衛東. 雙曲柄環板式針擺行星傳動降低振動與噪聲的優化設計與試驗[J]. 機械工程學報，2010，46(23)：53-60.

He Wei-dong. Optimum design and experiment for reducing vibration and noise of double crank ring-plate-type pin-cycloid planetary drive [J]. Journal of Mechanical Engineering, 2010, 46(23):53-60.

[11] Blagojevic M, Marjanovic N, Djordjevic Z. Numerical and experimental analysis of the cycloid disc stress state [J]. Tehnicki Vjesnik, 2014, 21(2): 377-382.

[12] Litvin F L. Design simulation of meshing, and contact stress for an improved worm gear drive [J]. Mechanism and Machine Theory, 2007, 42: 940-959.

[13] 劉志峰，張志民. 基于多項式的等高齒錐齒輪時變嚙合剛度建模[J]. 吉林大學學報：工學版，2013，43(4)：939-944.

Liu Zhi-feng, Zhang Zhi-min. Modelling of high-spiral bevel gear mesh stiffness based on polynomial [J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(4): 939-944.

[14] 周長江，唐進元. 齒輪傳動的線外嚙合與沖擊摩擦[J]. 機械工程學報，2008，44(3)：75-81.

Zhou Chang-jiang, Tang Jin-yuan. Corner contact and impact friction of gear drive [J]. Journal of Mechanical Engineering, 2008, 44(3): 75-81.