基于彈性連接結構的電動輪縱向振動特性

毛 鈺，左曙光，林 福，曹佳楠，鄭玉平

(同濟大學 新能源汽車工程中心,上海 201804)

0 引 言

電動輪系統是由輪胎懸架、輪轂電機及其控制器組成的多體和多物理場系統，電機的電磁激勵與結構動力學的相互耦合作用使得電動輪系統涌現出新的動力學問題[1-3]。在電動輪系統動力學問題研究方面，Luo等[4]考慮了輪轂電機電磁激勵特征，分析了路面不平度激勵和由于電機定轉子動態偏心引起不平衡磁拉力耦合作用下電動輪垂向振動響應。Wang[5]、Sun[6]等主要針對開關磁阻電機不平衡磁拉力引起的電動輪動力學問題進行了研究。目前電動輪系統所表現出的垂向振動問題得到了較為廣泛的研究，但關于輪轂電機轉矩特征引起的電動輪系統縱向動力學問題研究較少。清華大學李建秋等[7,8]指出由于電動輪系統的轉矩激勵未經緩沖直接作用于輪胎將會引起輪胎滑移率和縱向力波動等動力學現象。張立軍等[9]基于輪轂電機-輪胎總成非線性動力學模型分析了輪轂電機轉矩波動引起的輪胎縱向接地力的階次振蕩。但上述研究都沒有具體結合電動輪系統動力學特征對其縱向振動特性進行分析。

針對電動輪存在的動力學問題，學者提出了相應的結構改進方案對系統特性進行優化。在電動輪系統結構改進優化方面，Nagya[10]采用動態吸振器形式的電動輪將輪轂電機質量轉換為吸振器質量，利用分離出來的電機質量進行吸振。馬英等[11]利用彈簧阻尼機構實現了在輪轂電機與車軸之間安裝直線電機的電動輪結構，通過輪內主動減振改善了車輛平順性和輪胎接地性能。羅玉濤等[12]提出了一種新型內置懸置系統的電動輪拓撲結構方案，通過設置橡膠襯套將電機轉化為與簧上質量并聯的質量，改善車輛垂向動力學特性。上述減振方案主要針對路面不平度激勵引起的車輛垂向振動問題，對于輪轂電機轉矩波動激勵下縱向振動問題的減振效果并未進行討論，而且在進行優化改進效果評價時僅分析了單一車速(或電機轉速)下的振動特性，未考慮整個電機工作轉速范圍內的效果。

為分析并改善電動輪縱向振動問題，本文首先通過確定輪轂電機加速工況下轉矩波動特征和建立電動輪系統縱扭耦合振動模型，分析了現有輪轂電機和輪輞剛性連接的結構形式下電動輪系統縱向振動特性，并結合模態特征解釋了系統振動現象；其次采用了輪轂電機和輪輞彈性連接的結構形式以規劃電動輪系統模態特征，對比分析了彈性連接結構的減振效果；最后通過連接參數對振動特性的影響分析確定了能夠實現減振效果的彈性連接參數合理取值范圍。

1 基于剛性連接結構的電動輪振動特性分析

1.1 電動輪動力學建模及分析

參考前期研究[13]建立基于剛性環輪胎模型的電動輪縱扭耦合動力學模型，如圖1所示，具體為：輪胎等效為剛性的圓環，與輪輞通過胎側相連，胎側等效為徑向和周向的剛度和阻尼；輪輞和輪轂電機通過螺栓剛性相連，二者等效為同一集中質量；輪輞經懸架擺臂及襯套與車身在縱向連接，根據Kelvin-Voigt模型將橡膠襯套等效為彈簧和阻尼器的并聯。模型包括輪胎環和輪輞/電機等質量的面內扭轉和縱向平移自由度以及車身的縱向平移自由度。輪胎扭轉自由度和縱向平移自由度通過考慮輪胎松弛特性的瞬態刷子模型實現耦合。該模型對于反映輪轂電機轉矩波動下電動輪振動特性的適用性已通過臺架試驗得到驗證[14]。模型運動學方程如下所示：

圖1 基于剛性連接電動輪系統模型Fig.1 Electric wheel model based on rigid connection

(1)

式中：xb、xa分別為輪胎和輪輞/電機的縱向位移；θb、θa分別為輪胎和輪輞/電機的旋轉角；Fcx為輪胎的縱向力；Re為輪胎半徑；mb、ma、md、mu分別為輪胎、輪輞、電機和1/4車身的質量；Iby、Iay、Idy分別為輪胎、輪輞和電機的轉動慣量；kb、cb分別為輪胎的縱向剛度和阻尼；kbθ、cbθ分別為輪胎的旋轉剛度和阻尼；kux、cux分別為懸架襯套的剛度和阻尼；kc、cc分別為胎面的縱向剛度和阻尼。電動輪模型參數如表1所示。

表1 電動輪結構及電機相關參數Table 1 Parameters of electric wheel model

注：p為電極對數；Ld(Lq)為d(q)軸電感；φf為永磁體磁通。

根據線性系統理論可確定系統極點，具體可參考文獻[15]，并進而得到模態參數如表2所示。

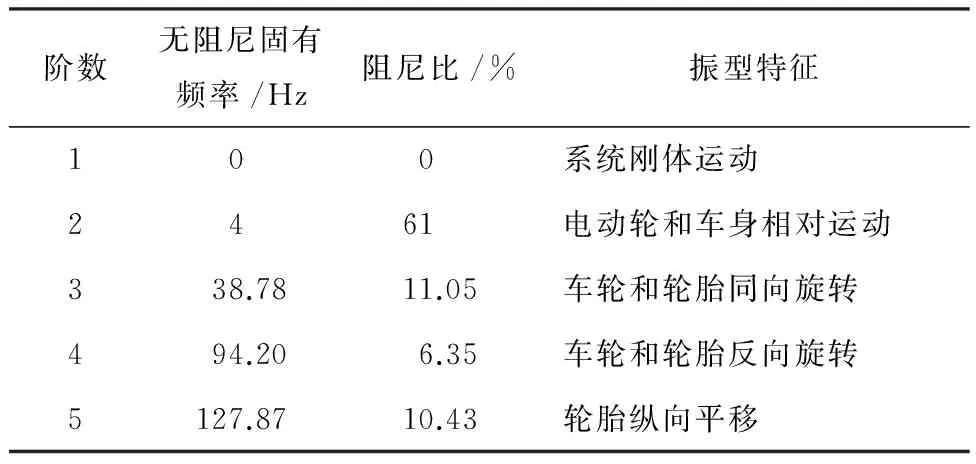
表2 剛性連接電動輪模態參數Table 2 Modal parameters of electric wheelwith rigid connection

1.2 輪轂電機轉矩波動分析

本文所研究的電動輪采用的輪轂電機為永磁同步電機，其轉矩波動主要來源于永磁體磁場非正弦分布、齒槽轉矩及電流諧波，該電機為分數槽集中繞組永磁同步電機，由于前期經過斜槽等結構改進優化，其轉矩波動受永磁體磁場非正弦分布、齒槽轉矩的影響比較小，主要取決于供電電流諧波，因此忽略電機結構特征，理想電機電磁轉矩模型為:

(2)

式中：id(iq)為d(q)軸電流；ia、ib、ic分別為A、B、C三相電流；θ為電機電角度；Te為電機輸出電磁轉矩。相關參數如表1所示。

根據仿真得到加速過程中的電機相電流，然后由式(2)確定輪轂電機電磁轉矩，分別如圖2、3所示。

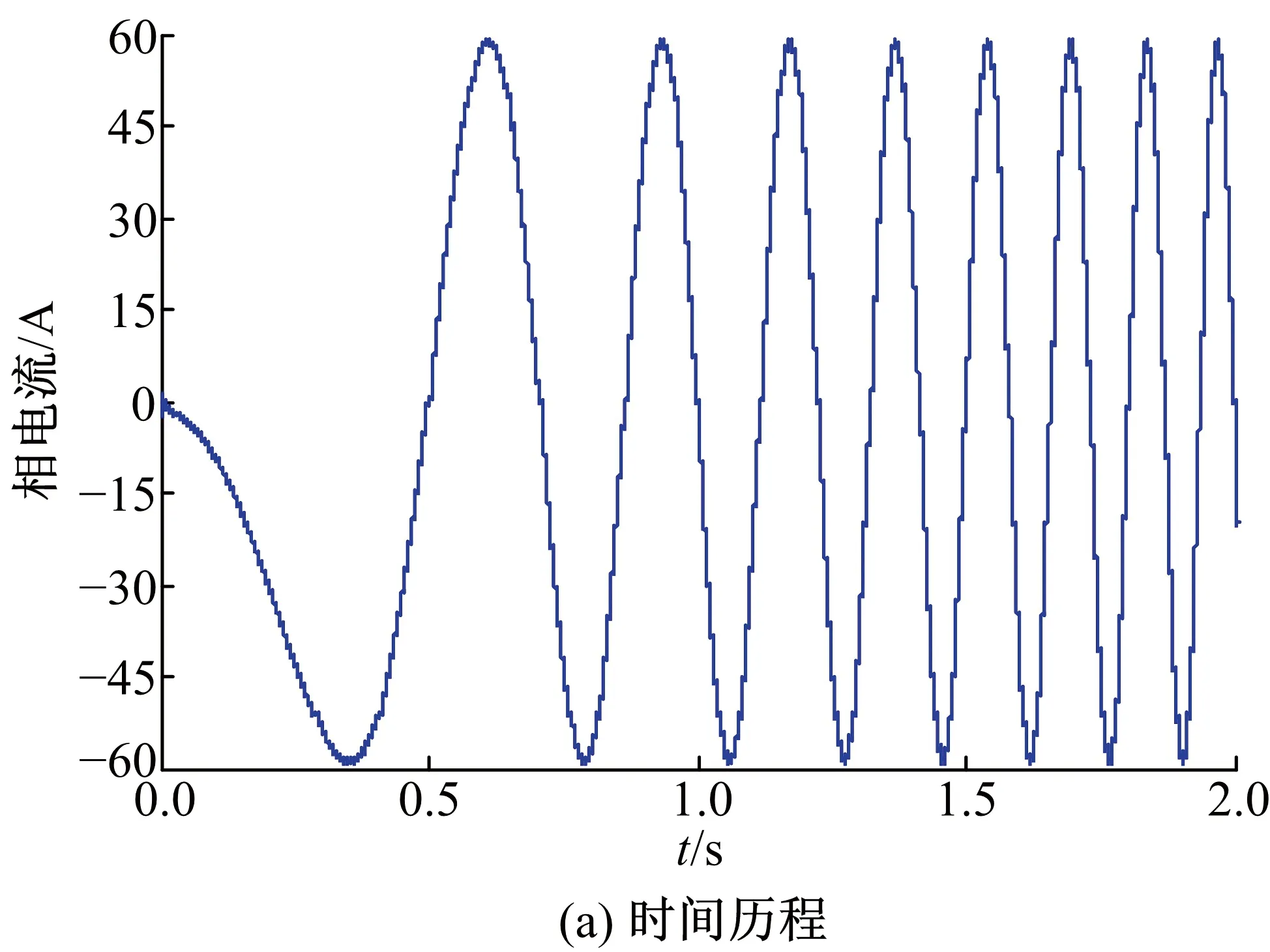
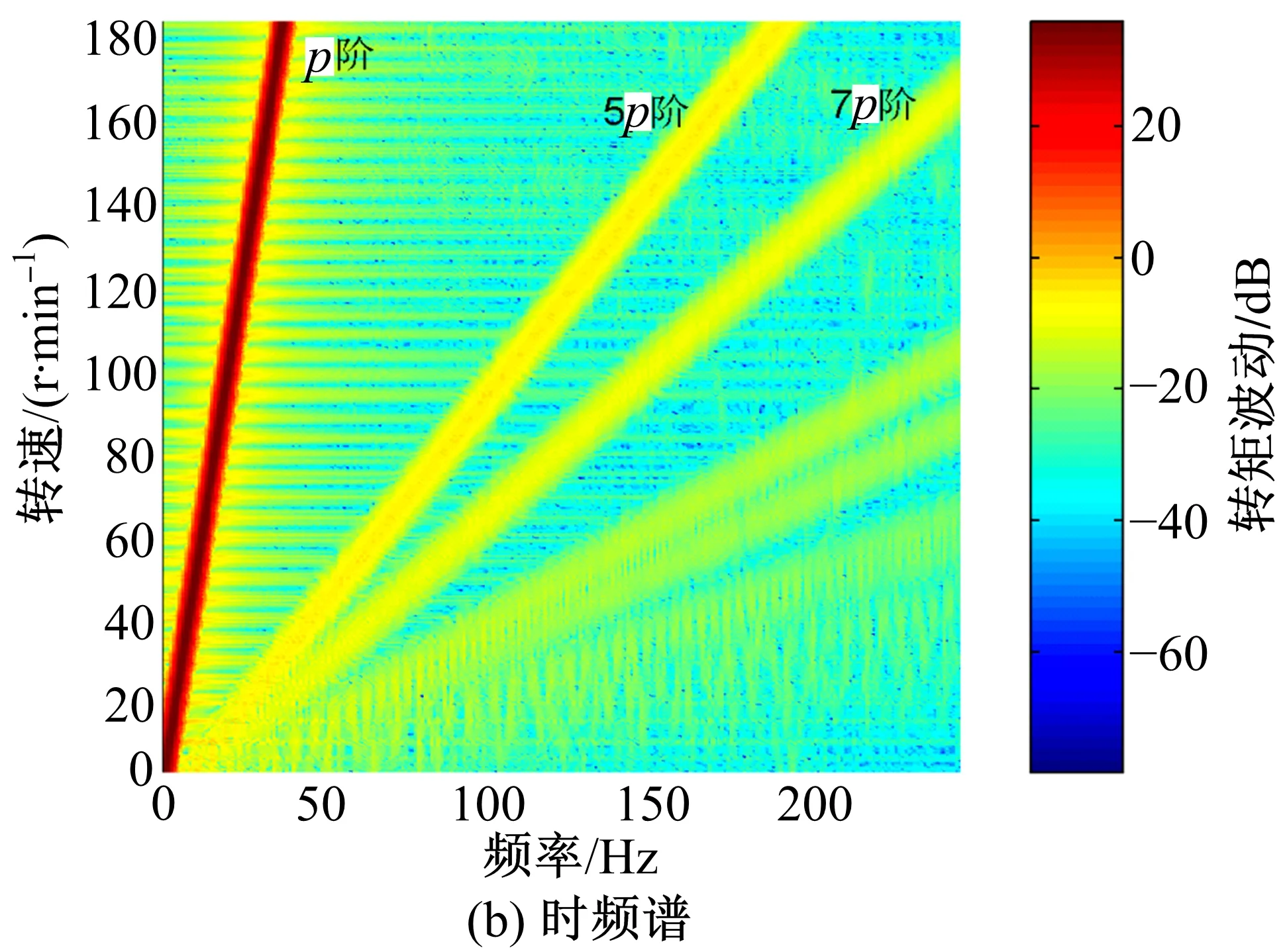
圖2 電機相電流信號Fig.2 Phase current of in-wheel motor

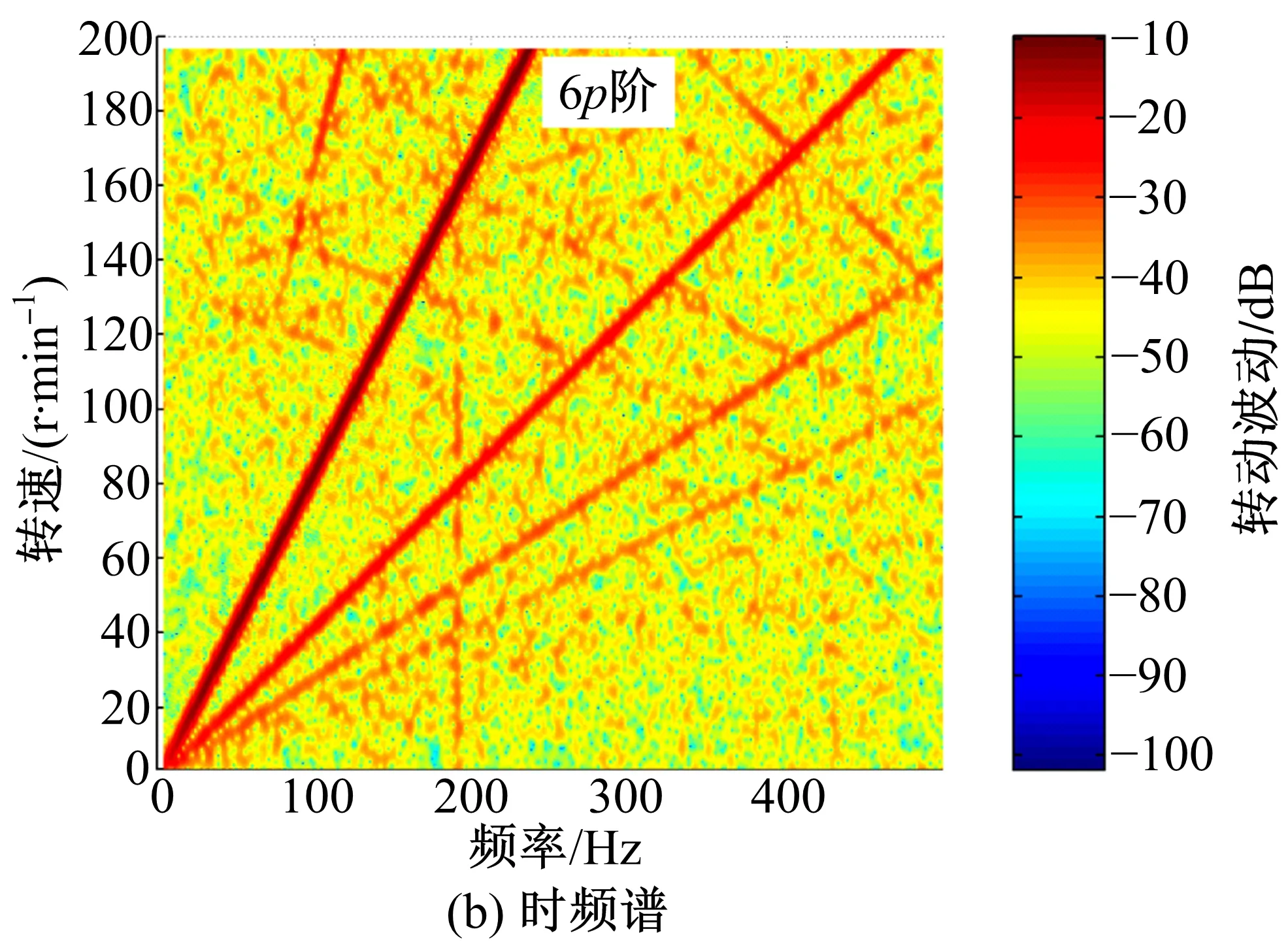
圖3 電機轉矩信號Fig.3 Electromagnetic torque of in-wheel motor

由圖2、圖3可知，電機相電流中除主導的基頻外還存在基頻5、7倍等諧波成分，電流諧波進而引起電機輸出轉矩波動，波動具有階次特征，主要階次為電流基頻的6階(對應轉頻的6p=72階)。轉矩波動直接作用于車輪將引起電動輪系統振動問題。

1.3 電動輪系統響應分析

考慮到輪轂電機轉矩波動具有階次特征，即轉矩波動頻率與轉速成正比，為反映電動輪在整個頻段內的振動特性，選取加速工況進行分析。將圖3所示的輪轂電機轉矩波動作用于電動輪縱扭耦合模型仿真得到了系統振動響應。圖4、圖5分別為轉矩波動激勵下輪胎和電機縱向振動加速度結果，在轉矩波動下系統表現出階次振動，主要振動階次為轉頻的6p階。

提取輪胎和電機6p階振動切片分別如圖6、圖7所示，輪胎振動主要集中在96 Hz，對應車輪和輪胎反向旋轉模態；電機振動主要集中在40 Hz，對應車輪和輪胎同向旋轉模態。電動輪同向和反向兩階旋轉模態對應頻率相差較大，使電動輪系統產生共振的敏感電機工作轉速范圍較寬(30～35 r/min和80～100 r/min)，電機轉速為33 r/min時，轉矩波動(頻率為40 Hz)激發電動輪同向旋轉模態，從而使電機振動顯著增加；電機轉速為80 r/min時，轉矩波動(頻率為96 Hz)激發電動輪反向旋轉模態，從而使輪胎振動變得突顯。針對上述問題，本文考慮輪輞和電機彈性連接的結構形式對電動輪系統縱向振動特性進行優化。

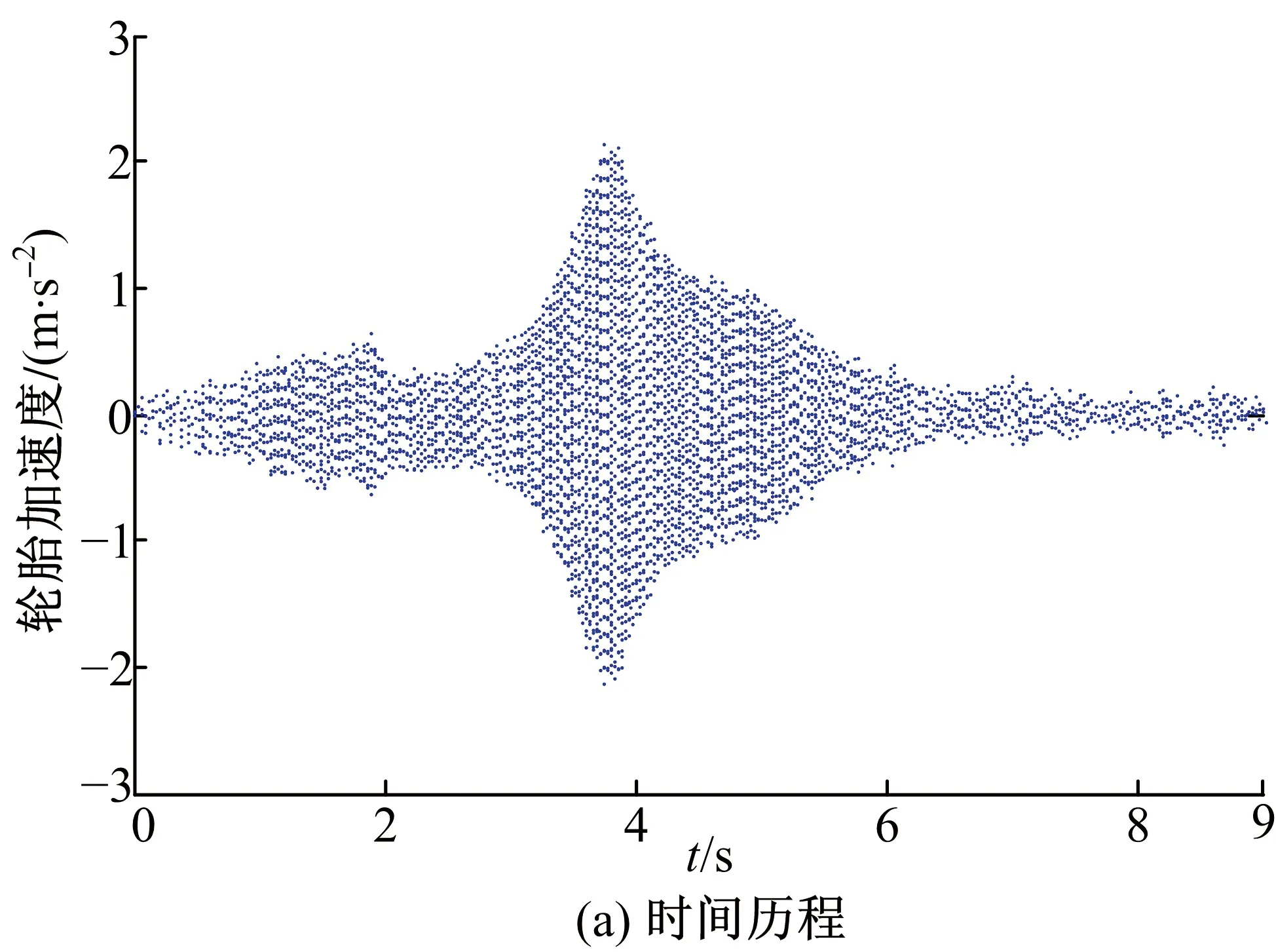
圖4 輪胎加速度信號Fig.4 Tire acceleration

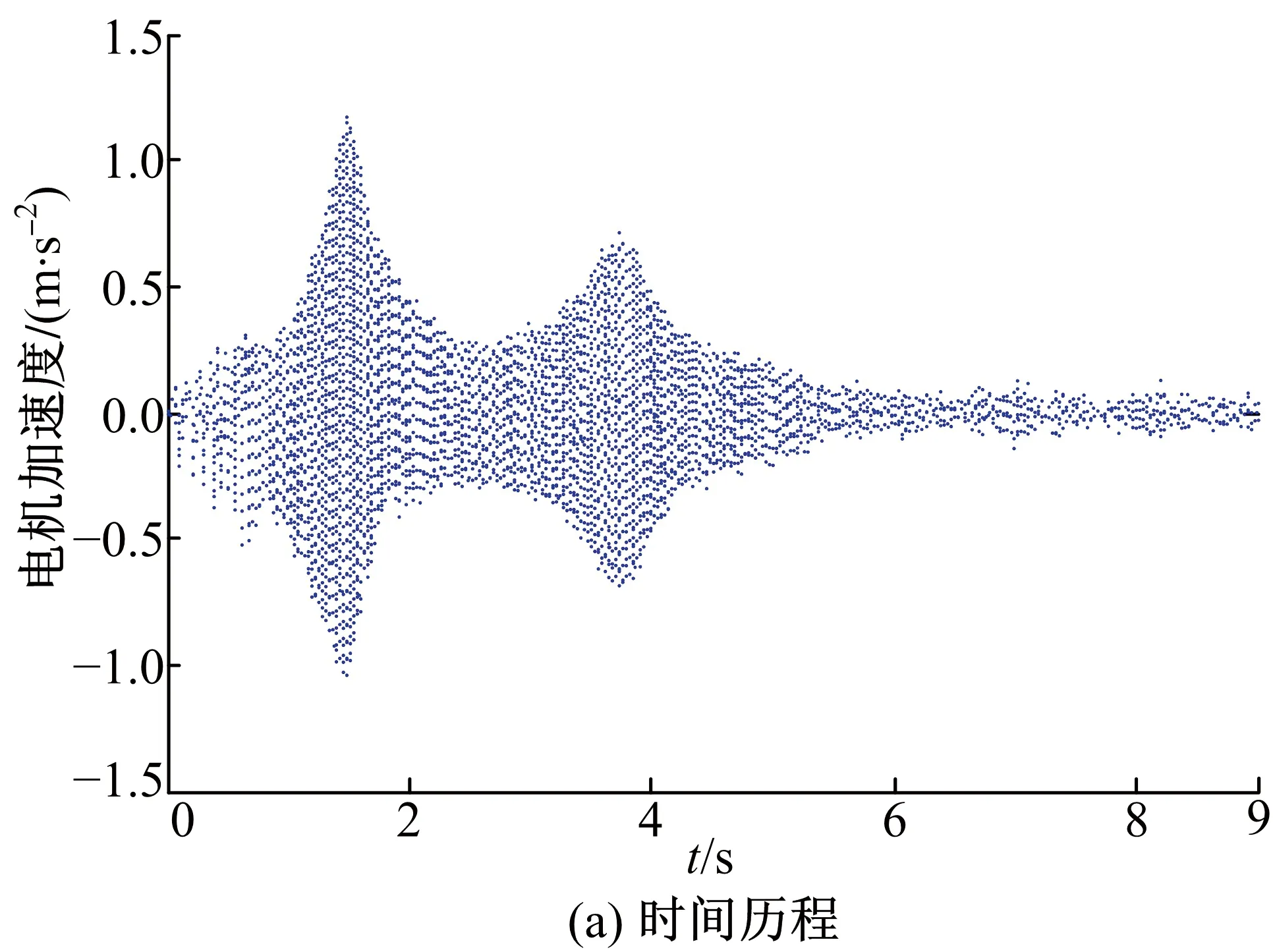
圖5 電機加速度信號Fig.5 Motor acceleration

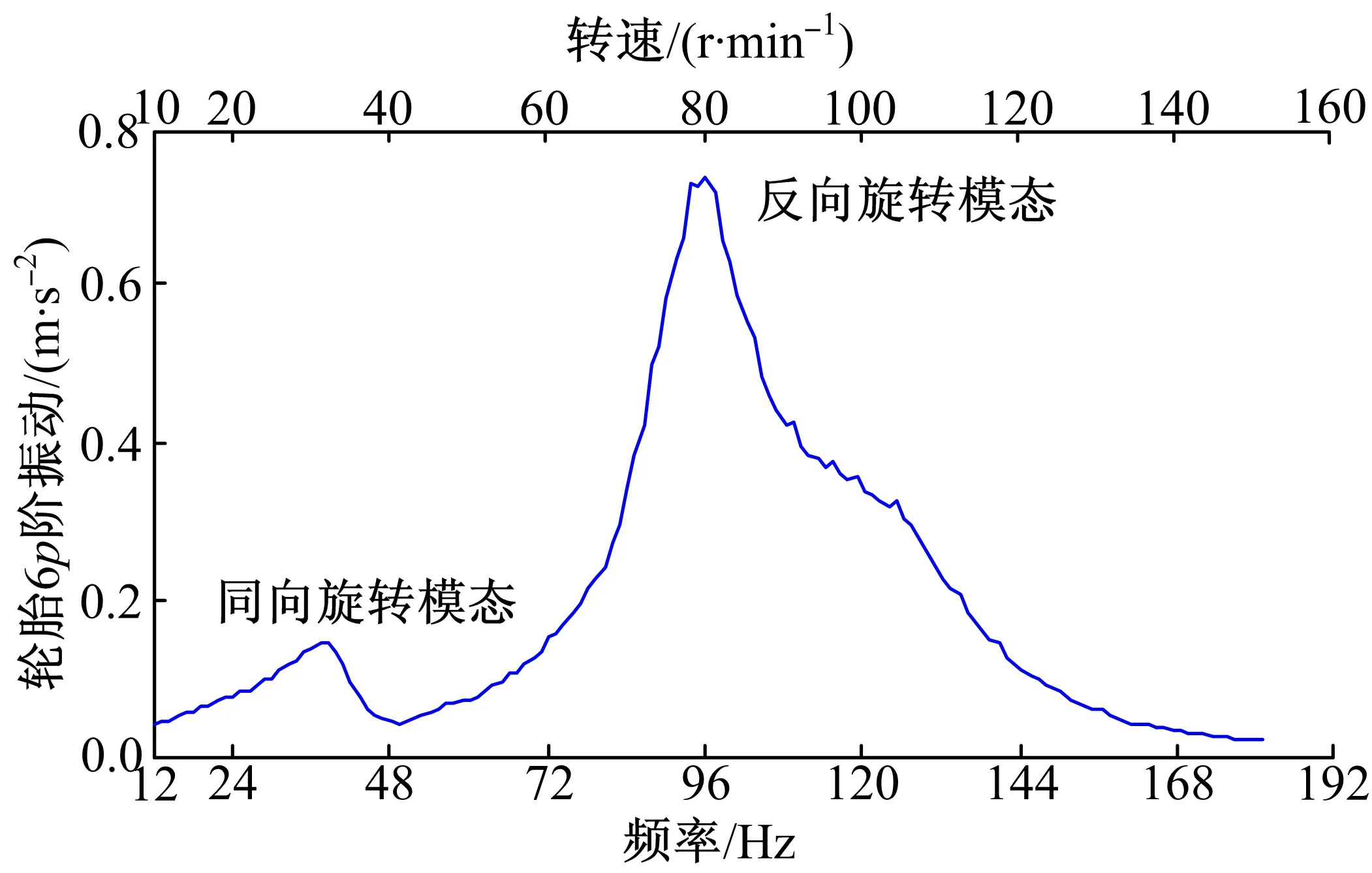
圖6 輪胎6p階振動Fig.6 6pth order vibration of tire

圖7 電機6p階振動Fig.7 6pth order vibration of motor

2 基于彈性連接結構的電動輪振動特性分析

2.1 考慮彈性連接的電動輪動力學建模

圖8為考慮彈性連接改進后的電動輪結構。輪轂電機內定子采用懸臂方式通過軸承支撐于轉子內端蓋，并通過花鍵與轉向節進行裝配實現其固定，附有表貼式永磁體的轉子與轉子內端蓋通過螺栓連接為一體，轉子內端蓋與輪輞內緣通過螺栓連接，圓周方向均布有5個螺栓以實現轉矩從轉子到輪輞的傳遞，并且在連接處填充橡膠材料構成扭轉減振結構以實現轉矩的柔性傳遞。相較于剛性連接布置形式，彈性連接方案在電動輪動力傳遞中引入緩沖減振結構，從而能夠改善電動輪系統振動特性。

圖8 考慮彈性連接的電動輪結構Fig.8 Electric wheel structure based on elastic connection

考慮輪輞和電機在徑向和周向的連接彈性得到如圖9所示的改進電動輪系統模型，與剛性連接模型不同之處在于輪輞和電機為通過彈簧連接的兩個集中質量，因此模型包括輪胎環、輪輞、電機等質量的面內扭轉和縱向平移自由度以及車身的縱向平移自由度。模型運動學方程為：

(3)

圖9 基于彈性連接的電動輪系統模型Fig.9 Electric wheel model based on elastic connection

式中：xa、xd分別為輪輞和電機的縱向位移；θa、θd分別為輪輞和電機的旋轉角；kd、cd分別為輪輞和電機的等效縱向連接剛度和阻尼；kdθ、cdθ分別為輪輞和電機的等效周向連接剛度和阻尼。由于電動輪周向均布有n=5個連接螺栓，連接半徑r=0.15 m。在連接螺栓處布置橡膠懸置，由單個懸置的剛度k和阻尼c按下式確定連接參數：

(4)

參照文獻[12]根據經驗仿真時設置k=6×104N/m,c=100 N·s/m。

2.2 考慮彈性連接的電動輪動力學分析

由式(3)確定的考慮彈性連接的電動輪縱扭耦合振動方程是線性定常的，基于線性系統理論進行分析確定電動輪系統模態特征如表3所示。

表3 彈性連接電動輪模態參數Table 3 Modal parameters of electric wheel withelastic connection

考慮彈性連接后釋放了輪輞的縱向平移和周向旋轉自由度，因此相對剛性連接增加了第6和第7階模態，振型即表現為輪輞的縱向平移和周向旋轉。另外，考慮彈性連接后對電動輪系統振動貢獻較大的兩階旋轉模態對應頻率有所降低，而且相互靠近；同時由于橡膠懸置的阻尼作用，兩階旋轉模態阻尼比有所增加。

2.3 考慮彈性連接的電動輪系統振動響應

將輪轂電機轉矩波動施加于考慮彈性連接的電動輪系統模型，得到輪胎和電機縱向加速度響應，并與剛性連接時的振動響應進行對比，如圖10、圖11所示。

新增的6、7兩階輪輞運動模態對系統振動貢獻較小，在輪胎和電機縱向振動中占主導作用的仍然是電動輪旋轉模態，由于兩階旋轉模態頻率降低，彈性連接電動輪結構形式下輪胎和輪輞振動峰值往低頻移動，即彈性連接結構形式能夠有效衰減轉矩波動引起的在45 Hz和100 Hz附近的中頻振動，但同時會在24～30 Hz低頻處引起系統共振，低頻振動峰值較之前的中頻振動峰值小。在彈性連接情況下電動輪系統出現的兩處主導共振頻率更為接近，其敏感轉速范圍(20～25 r/min)相比剛性連接時的敏感轉速范圍更窄，在整個電機工作轉速范圍內產生的振動影響更小。

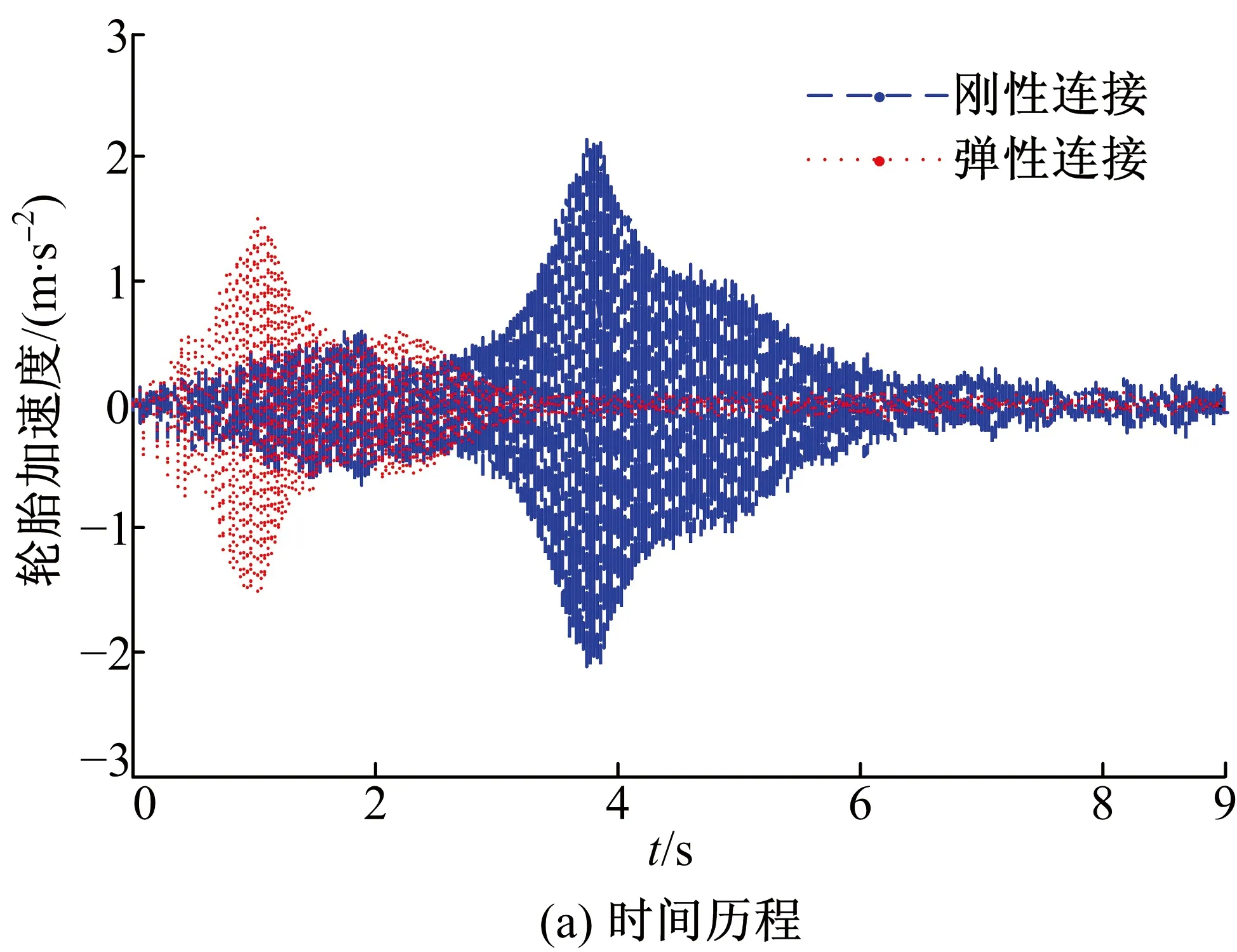
圖10 剛性連接與彈性連接時輪胎振動加速度對比Fig.10 Comparison of tire vibration between rigidand elastic connection

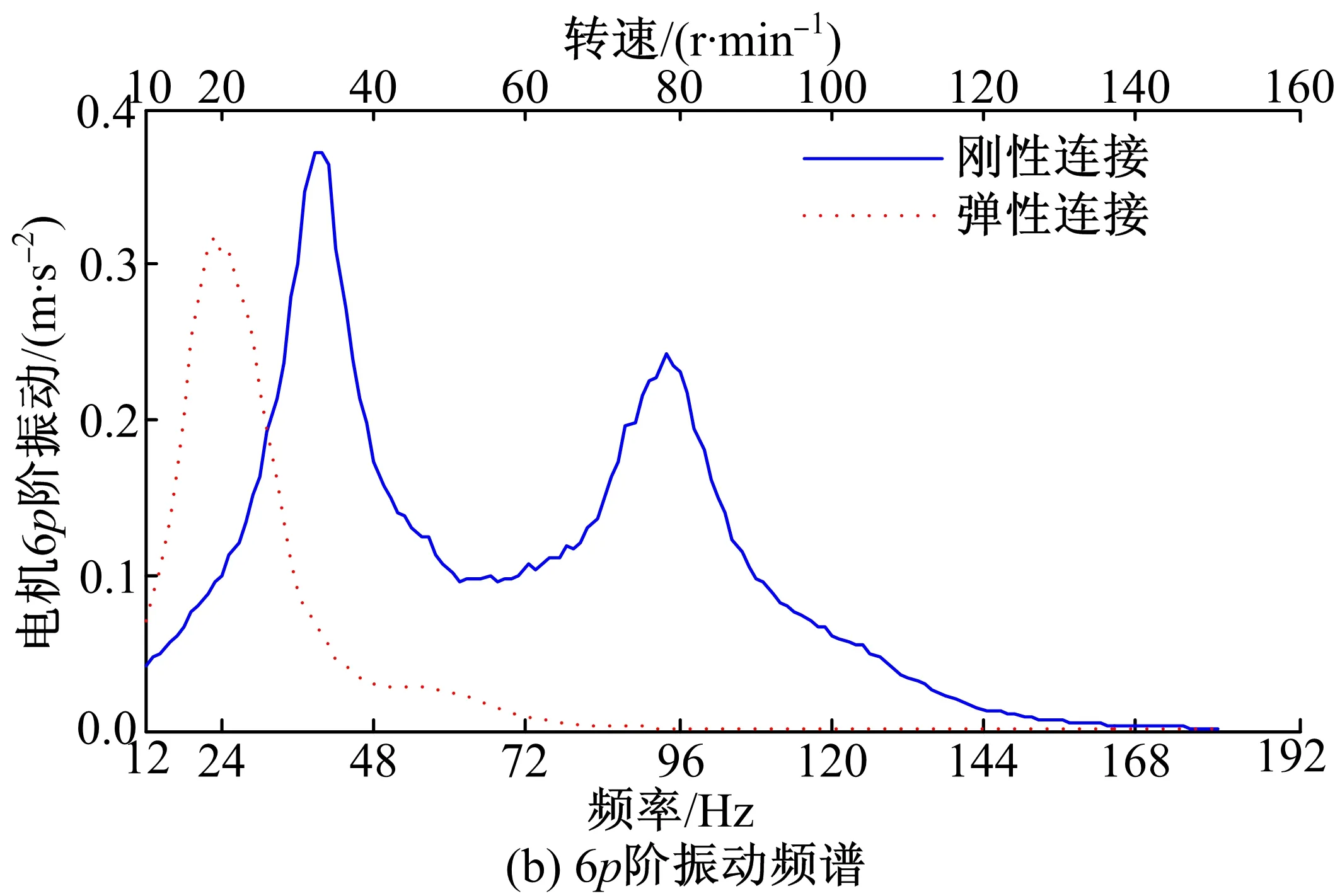
圖11 剛性連接與彈性連接時電機振動加速度對比Fig.11 Comparison of motor vibration between rigidand elastic connection

3 彈性連接參數對電動輪系統振動的影響分析

輪轂電機和輪輞彈性連接布置改變了電動輪系統模態頻率分布，使對系統振動貢獻較大的兩階旋轉模態往低頻移動，因此在電機整個工作轉速范圍內能夠有效衰減原模態頻率(100 Hz)附近的中頻振動，但同時會在較低頻率處出現新的共振峰值。彈性連接結構通過規劃電動輪系統模態特征為其振動特性的優化提供了更大的空間，為合理設計彈性連接結構需研究連接參數對電動輪系統模態參數及振動特性的影響。

圖12、圖13分別為不同連接剛度輪胎和電機頻響函數對比。連接剛度會對電動輪系統在整個頻段內的振動產生影響，隨著連接剛度的減小，輪胎和電機的共振峰往低頻移動，當連接剛度較大時，新出現的共振峰值較剛性連接時更顯著，對整個頻段內系統振動特性而言，彈性連接并未有效衰減振動，如表4所示，對于該連接參數轉矩波動下輪胎和電機振動均方根值相比剛性連接時有一定的增加；當剛度較小時，共振峰值明顯下降，而且共振帶寬較小，相對剛性連接在整個頻帶內振動影響更小，如表4所示，輪胎和電機振動加速度均方根值有所下降。因此為使彈性連接結構能夠具有較好的減振效果，彈性連接剛度需控制在一定范圍內。

圖12 不同連接剛度下輪胎頻響函數Fig.12 Frequency response of tire vibration underdifferent connection stiffness

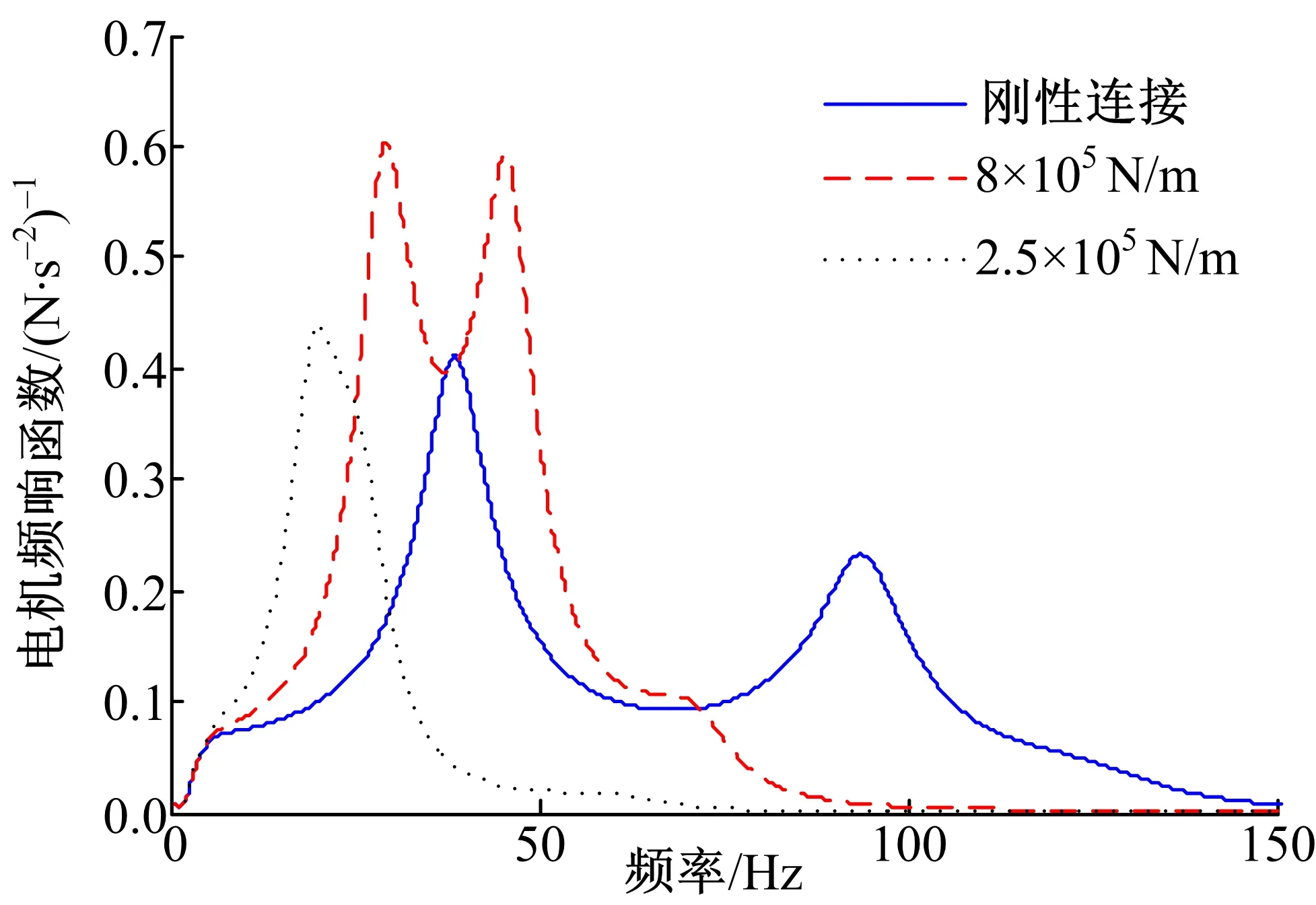
圖13 不同連接剛度下電機頻響函數Fig.13 Frequency response of motor vibration underdifferent connection stiffness

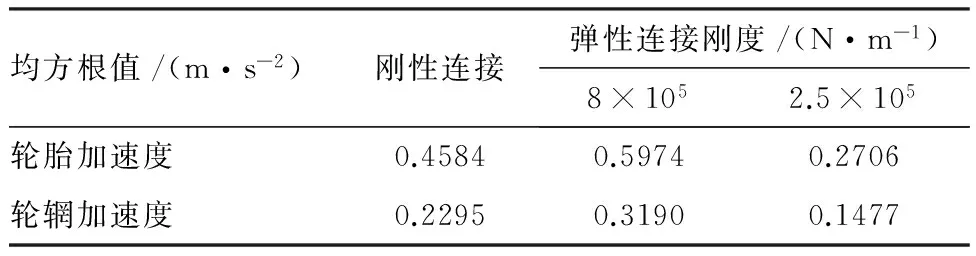
表4 振動均方根值對比Table 4 Comparison of vibration RMS underdifferent connection stiffness

圖14、圖15分別為不同連接阻尼下輪胎和電機的頻響函數對比。連接阻尼的改變不影響共振出現的頻率，僅對共振峰幅值有影響，隨著阻尼的增加，旋轉模態頻率處的共振峰值有一定的下降。

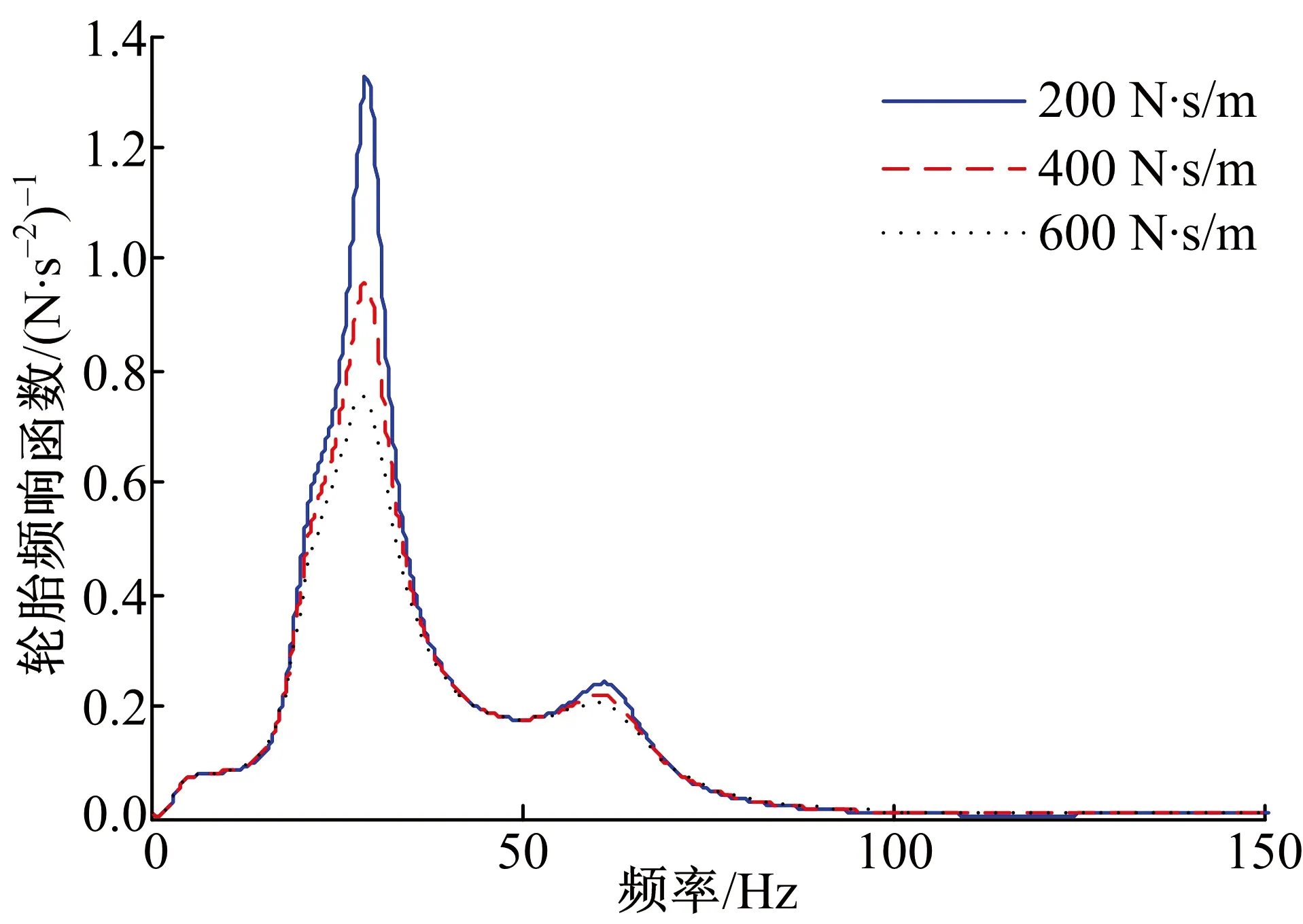
圖14 不同連接阻尼下的輪胎頻響函數Fig.14 Frequency response of tire vibration underdifferent connection damping

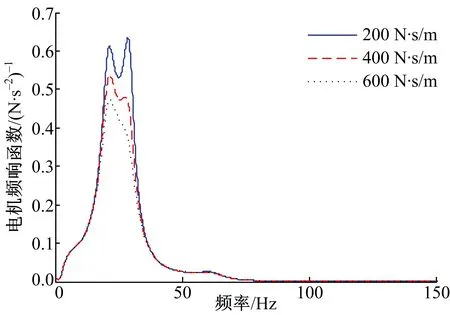
圖15 不同連接阻尼下的電機頻響函數Fig.15 Frequency response of motor vibration underdifferent connection damping

為進一步確定能夠使彈性連接結構具有較好減振效果的連接參數取值范圍，仿真得到轉矩波動下輪胎和電機縱向振動加速度均方根值隨彈性連接參數變化分別如圖16、圖17所示。由于連接剛度會改變電動輪系統各共振峰的相對位置和幅值，從而對整個頻段內的振動產生影響，而連接阻尼只改變共振峰幅值，僅影響旋轉模態頻率處的振動，所以連接剛度比連接阻尼對電動輪系統振動影響大，振動指標隨連接剛度變化更明顯。輪胎和電機振動指標隨連接剛度增加而增加，當連接阻尼較小時其增加趨勢更明顯。輪胎和電機振動指標隨連接阻尼增加而降低，當阻尼增加到一定程度時其變化趨于平緩。

圖16 輪胎振動均方根值隨連接參數的變化Fig.16 Variations of tire vibration RMS withconnection parameters

圖17 電機振動均方根值隨連接參數的變化Fig.17 Variations of motor vibration RMS withconnection parameters

圖16、圖17中灰色平面為剛性連接時輪胎和電機加速度均方根水平，由圖中曲面交線確定合理的彈性連接參數范圍如圖18所示。為使彈性連接結構具備減振效果應使彈性連接剛度較低而連接阻尼較大，即圖中虛線下方，而且越靠近右下角區域其減振效果越好。但考慮到動力傳遞的可靠性需求和相對運動空間的限制，連接剛度不宜過小，基于上述因素可進一步縮小連接參數的有效區域。

圖18 連接參數有效取值區間Fig.18 Effective area of connection parameters values

4 結 論

(1)輪轂電機轉矩波動激勵下電動輪系統表現出縱向振動，對振動貢獻較大的模態為輪胎和車輪間的同向旋轉和反向旋轉模態。在現有剛性連接結構下由于兩階旋轉模態頻率相距較大，電動輪系統在電機工作范圍內整體振動特性較差。

(2)采用輪轂電機和輪輞彈性連接的結構方式能夠降低電動輪系統兩階旋轉模態頻率并使二者相互靠近，因此在電機整個工作轉速范圍內能夠有效衰減原模態頻率(100 Hz)附近的中頻振動，縮短了使電動輪系統產生共振的敏感電機轉速范圍，根據連接參數的影響規律進一步確定電動輪彈性連接參數的合理取值范圍，本文的研究為電動輪系統采用彈性連接構型進行優化設計提供了參考。

[1] Tahami F, Kazemi R, Farhanghi S. A novel driver assist stability system for all-wheel-drive electric vehicle [J]. IEEE Transactions on Vehicular Technology, 2003, 52(3): 683-692.

[2] Chen Y, Wang J M. Design and evaluation on electric differentials for overactuated electric ground vehicles with four independent in-wheel motors [J]. IEEE Transactions on Vehicular Technology, 2012, 61(4): 1535-1542.

[3] Wang R, Chen Y, Feng D, et al. Development and performance characterization of an electric ground vehicle with independently-actuated in-wheel motors [J]. Journal of Power Sources,2011,196(8): 3962-3971.

[4] Luo Y T, Tan D. Study on the dynamics of the in-wheel motor system [J]. IEEE Transactions on Vehicular Technology, 2012, 61(8): 3510-3518.

[5] Wang Y Y, Li P, Ren G. Electric vehicles with in-wheel switched reluctance motors: coupling effects between road excitation and the unbalanced radial force [J]. Journal of Sound and Vibration, 2016, 372: 69-81.

[6] Sun W, Li Y, Huang J, et al. Vibration effect and control of in-wheel switched reluctance motor for electric vehicle [J]. Journal of Sound and Vibration, 2015, 338: 105-120.

[7] Song Z Y,Li j,Wei Y T, et al. Interaction of in-wheel permanent magnet synchronous motor with tire dynamics [J]. Chinese Journal of Mechanical Engineering，2015, 28(3): 470-478.

[8] Li J Q,Song Z Y,Wei Y T,et al. Influence of tire dynamics on slip ratio estimation of independent driving wheel system [J]. Chinese Journal of Mechanical Engineering， 2015, 27(6): 1203-1209.

[9] 張立軍，錢敏，余卓平. 輪轂電機-輪胎總成非線性動力學特性仿真分析[C]∥第五屆中國智能交通年會暨第六屆國際節能與新能源汽車創新發展論壇優秀論文集(下冊)， 北京: 電子工業出版社, 2009: 162-168.

[10] Nagya Go. Development of an in-wheel drive with advanced dynamic-damper mechanism [J]. JSAE Review, 2003, 24(4): 477-481.

[11] 馬英, 鄧兆祥, 謝丹. 電動輪車輛輪內主動減振系統設計與研究[J]. 系統仿真學報, 2014, 26(11): 2770-2778.

Ma Ying, Deng Zhao-xiang, Xie Dan. Design and study of active suspension system on electric vehicles with In-wheel-motor [J]. Journal of System Simulation, 2014, 26(11): 2770-2778.

[12] 羅玉濤, 譚迪. 一種帶新型內置懸置系統的電動輪結構研究[J]. 汽車工程, 2013, 35(12): 1105-1110.

Luo Yu-tao, Tan Di. A research on the hub-motor driven wheel structure with a novel built-in mounting system[J]. Automotive Engineering, 2013, 35(12): 1105-1110.

[13] 毛鈺, 左曙光, 林福. 轉矩波動下電動輪系統機電耦合振動特性[J]. 吉林大學學報:工學版, 2017 , 47 (3):908-916.

Mao Yu， Zuo Shu-guang，Lin Fu. Electromechanical coupled vibration characteristics of electric wheel under torque ripple [J]. Journal of Jilin University (Engineering and Technology Edition), 2017,47(3):908-916.

[14] 左曙光，段向雷，吳旭東. 電動輪-懸架系統臺架振動特性試驗分析[J]. 振動與沖擊, 2014, 33(12): 165-187.

Zuo Shu-guang, Duan Xiang-lei, Wu Xu-dong. Vibration test analysis of a electric wheel-suspension system on a test bed [J]. Journal of Vibration and Shock, 2014, 33(12): 165-187.

[15] 毛鈺，左曙光，林福, 等. 轉矩波動下電動輪縱向階次振動特性試驗及理論分析[J]. 同濟大學學報:自然科學版, 2016, 44(11): 1735-1742.

Mao Yu, Zuo Shu-guang, Lin Fu, et al. Experimental and theoretical analysis for horizontal order vibration characteristics of electric wheel under torque ripple [J]. Journal of Tongji University(Natural Science), 2016, 44(11): 1735-1742.