基于疲勞和13°沖擊性能的組裝式車輪優化設計

王登峰，張 帥，汪 勇，陳 輝

(吉林大學 汽車仿真與控制國家重點實驗室，長春 130022)

0 引 言

車輪是汽車行駛系中最主要的承載件，其綜合性能是衡量汽車性能的重要指標之一；同時，作為非簧載質量，其輕量化程度對汽車性能有重要影響[1]。

在車輪疲勞試驗性能的仿真分析上，Shang等[2]對鋼制車輪沖壓過程進行了仿真分析和試驗驗證，研究了殘余應力對車輪彎曲疲勞壽命的影響；Ballo等[3]通過材料拉伸試驗得到A356-T6鋁合金車輪的S-N曲線，仿真分析了車輪的彎曲疲勞壽命和應變并得到了試驗驗證；Oery等[4]研究了輪胎參數在徑向疲勞試驗仿真分析中的作用，結果表明輪胎豎直剛度對徑向疲勞預測有重要影響。

從Bends?e 等[5]提出拓撲優化的均勻化方法以來，拓撲優化的方法在結構優化設計中得到了深入發展和應用[6-9]。Zhang等[10]對鋁合金車輪進行了拓撲優化，并仿真分析了優化后車輪的強度和剛度。Hu等[11]以輪輞和輪緣厚度為設計變量、彎曲疲勞和徑向疲勞工況的車輪最大應力為約束并以車輪質量最小為目標，對鋁合金車輪進行了優化。Xiao等[12]基于彎曲疲勞試驗對鋼制車輪進行了多目標拓撲優化，以柔度和模態頻率為目標對車輪進行輕量化設計，并進行了應力分析和試驗驗證。

國內外學者在車輪13°沖擊性能的仿真分析上取得了不少成果。臧孟炎等[13]對鋁合金車輪13°沖擊過程進行仿真分析，比較了仿真和試驗的車輪應變，確認了有限元模擬的有效性。尹冀等[14]基于不同應變率下的輪轂材料本構模型對車輪13°沖擊試驗進行了有限元模擬，結合試驗驗證了仿真模型的有效性。Chang等[15]對車輪13°沖擊試驗進行了有限元仿真，分析了車輪的應變能密度，通過試驗對比得出總塑性功可以預測車輪的失效。鄭玉卿等[16]用Abaqus分析了鑄鋁車輪的13°沖擊，以等效塑性應變作為損傷指標判定車輪是否滿足動態沖擊測試標準。Vinothkumar等[17]使用Abaqus對車輪13°沖擊進行了仿真分析，通過與試驗測得的主應變對比，驗證了有限元分析的正確性。閆勝昝等[18]通過仿真分析研究了充氣壓力對鋁合金車輪沖擊試驗和徑向載荷試驗車輪應力值的影響。Tsai等[19]通過ANSYS分析了鋁合金車輪的13°沖擊試驗，在車輪沒有裝配輪胎的情況下，仿真研究了輪胎吸能0%、20%和40%三種工況下鋁合金車輪的應變。張響[20]模擬了鋁合金車輪的低壓鑄造，進行了疲勞壽命和沖擊試驗的簡化仿真分析，實現了工藝過程模擬與結構有限元模擬的仿真技術集成。Chauhan等[21]對車輪13°和90°沖擊進行了仿真分析，并通過試驗驗證了車輪等效塑性應變和應變能密度對車輪失效預測的有效性。此外，國內外學者在車輪新材料的應用和輪胎對沖擊試驗仿真的影響方面也進行了研究[22-25]。

綜上可知，以上研究多集中在疲勞和沖擊試驗的仿真分析和試驗驗證上，或者是研究車輪應變和應變能密度對車輪失效的預測；在優化設計中將沖擊性能僅用作檢驗校核優化后的車輪，而不是直接作為約束條件；車輪輕量化設計時沒有對車輪進行參數化，而是在參數化階段設置多組模型進行對比或者僅將車輪厚度作為設計變量，極大減弱了車輪結構的變形能力，優化空間和效果有限。同時，以上研究僅涉及概念設計階段基于疲勞試驗的拓撲優化，沒有研究參數化階段的多目標優化；沒有綜合研究疲勞性能和沖擊性能與車輪結構的關系；所研究的車輪均為單一材料的整體式結構，沒有研究異種材料連接的組裝式車輪。

1 動態疲勞試驗參數設置

根據《乘用車車輪性能要求和試驗方法》(GB/T 5334-2005)，車輪應滿足動態彎曲疲勞試驗和動態徑向疲勞試驗要求。

1.1 動態彎曲疲勞試驗參數

車輪動態彎曲疲勞試驗方法如圖1所示。試驗時在加載軸末端施加力F產生彎矩，車輪在恒定的彎矩作用下旋轉，達到10萬次循環前車輪不能出現新可見裂紋、加載點位移偏移量不能超過初始全加載位移偏移量的20%。

取加載軸長度L=1 m。試驗彎矩M(N·m)和加載力F(N)滿足下式：

M=(μR+d)FvS

(1)

(2)

式中：μ為輪胎與路面間的摩擦因數；R為輪胎靜負荷半徑(m)；d為車輪偏距(m)；Fv為車輪最大垂直靜負荷(N)；S為強化試驗系數。

圖1 車輪動態彎曲疲勞試驗示意圖Fig.1 Schematic diagram of wheel dynamicbending fatigue test

結合車輪型號，試驗參數確定如下：μ=0.7，R=0.316 m，d=0.053 m，Fv=6027 N，S=1.6。由式(1)和式(2)可知：M=2644 N·m，F=2644 N。

1.2 動態徑向疲勞試驗參數

車輪動態徑向疲勞試驗方法如圖2所示。車輪在試驗臺上轉動時，轉鼓向其傳遞徑向負荷Fr，在循環50萬次前車輪不能出現新可見裂紋。

圖2 車輪動態徑向疲勞試驗示意圖Fig.2 Schematic diagram of wheel dynamic radial fatigue test

車輪的徑向負荷Fr(N)，滿足下式：

Fr=FvK

(3)

式中：Fv為車輪最大垂直靜負荷(N)；K為強化試驗系數。

結合車輪型號，試驗參數確定如下：Fv=6027 N，K=2.25。根據式(3)，則Fr=13561 N。車輪充氣壓力選為0.45 MPa。

車輪的徑向負荷通過輪胎對稱加載在輪輞兩側的胎圈座上，并在2θ0角度內成余弦分布，如圖3所示。

圖3 車輪徑向加載示意圖Fig.3 Schematic diagram of wheel radial loading

在圖3中設立柱坐標系，設單側胎圈座受力為F，加載處半徑為rb(mm)，加載面的寬度為b(mm)，單個加載壓力為A(MPa)、與豎直方向夾角為θ(rad)，則加載壓力的余弦振幅A0(MPa)推導如下：

(4)

(5)

根據Stearns等[26]研究，θ0取2π/9時最能模擬載荷的真實情況。結合車輪型號，rb=202.8 mm，b=20 mm。根據式(5)，A0=1.88 MPa。

2 組裝式車輪設計

圖4 車輪概念設計模型Fig.4 Concept design model of wheel

2.1 車輪聯合拓撲優化建模

在車輪概念設計模型中裝配1 m長的加載軸，將該模型導入HyperMesh中進行幾何清理，并采用四面體單元進行網格劃分。其中，輪輞單元大小為4 mm、輪輻拓撲空間單元大小為5 mm、加載軸單元大小為10 mm，允許最小尺寸均為2 mm。共離散為417049個單元，94754個節點。

設置動態彎曲疲勞試驗和動態徑向疲勞試驗兩個工況，進行車輪聯合拓撲優化。動態彎曲疲勞試驗工況下，加載軸和車輪安裝面之間的螺栓連接用RBE2模擬，約束輪輞內側外沿節點的全部自由度，在加載軸末端施加2644 N的力。動態徑向疲勞試驗工況下，約束車輪安裝面上5個螺栓孔的全部自由度，胎圈座2θ0內加載振幅為1.88 MPa的余弦壓力，兩胎圈座之間的輪輞外表面上加載0.45 MPa的充氣壓力。車輪聯合拓撲優化的有限元模型，如圖5所示。

圖5 車輪聯合拓撲優化有限元模型Fig.5 Finite element model for united topologyoptimization of wheel

輪輞、輪輻和加載軸分別賦予鎂合金AZ91D，鋁合金6061和A3鋼的材料屬性。各材料參數如表1所示。

表1 材料參數Table 1 Material parameters

有限元分析時，使用材料的許用應力作為應力約束來保障車輪的強度，鎂、鋁合金的安全系數s取1.2來計算許用應力，材料屬性見表2。

表2 鎂、鋁合金材料屬性Table 2 Materialproperties of magnesium alloyand aluminum alloy

2.2 車輪聯合拓撲優化

在優化設計中，把剛度增大問題等效為柔度減小問題來研究，柔度則用應變能來定義[29,30]。多個工況的柔度加權和即為加權柔度，如下式所示:

(6)

在Optistruct中進行聯合拓撲優化。為了模擬動態疲勞試驗時載荷的周向動態變化，添加周向對稱約束[31]。為了模擬車輪的鍛壓工藝，添加拔模約束。為了清晰觀測拓撲優化結果中的材料分布，添加最小密度單元約束，約束單元最小尺寸為2 mm。約束車輪的強度和剛度，車輪強度用許用屈服應力約束，動態彎曲疲勞試驗工況的車輪剛度通過車輪節點的最大偏移量約束，動態徑向疲勞試驗工況的車輪剛度通過車輪的加權柔度約束。以車輪單元密度為設計變量，最大von Mises應力、節點最大偏移量為約束條件，質量最小為目標函數進行聯合拓撲優化。拓撲優化的數學模型為：

式中：m(ρ)為車輪質量(t)；σb(ρ)和σr(ρ)分別為動態彎曲疲勞試驗和動態徑向疲勞試驗工況下輪輻的最大von Mises應力(MPa)；σd為輪輻許用屈服應力(MPa)，σd=158.3 MPa；D(ρ)為動態彎曲疲勞試驗工況下車輪節點的最大偏移量(mm)；D0為車輪節點許用偏移量(mm)，D0=0.8 mm；Cr(ρ)為動態徑向疲勞試驗工況下車輪的加權柔度(N·mm)；Cr0為車輪柔度許用值(N·mm)，Cr0=3800 N·mm；ρ為單元密度。

2.3 車輪聯合拓撲優化結果

設置車輪的單元密度為0.3時，車輪聯合拓撲結果如圖6所示。

圖6 車輪聯合拓撲優化結果Fig.6 United topology optimization results of wheel

如圖6所示，拓撲優化結果中車輪的材料分布由內部的應力傳遞路徑決定，材料密度與應力值有關。動態彎曲疲勞試驗時，彎矩沿著車輪安裝面螺栓孔從輪輻傳遞到輪輞并依次遞減。動態徑向疲勞試驗時，兩胎圈座之間的輪輞表面受均勻氣壓，胎圈座承受了在2θ0角度內成余弦分布的徑向負荷，應力沿著輪輞向輪輻擴散。所以聯合拓撲優化時，輪輻根部形狀受動態彎曲疲勞試驗工況影響大；輪輞和輪輻交接處受動態徑向疲勞試驗工況影響大，該處材料密度分布均勻，在設計組裝式車輪時可以設計成圓環。

2.4 組裝式車輪建模

在HyperView中，將聯合拓撲優化的車輪結構導出三維幾何模型。參照該模型尺寸，在UG中建立拓撲優化后的組裝式車輪模型，如圖7所示。

圖7 組裝式車輪模型Fig. 7 Assembled wheel model

3 車輪13°沖擊性能分析

3.1 試驗工況

根據《道路車輛輕合金車輪沖擊試驗方法》(GB/T 15704-2012)，車輪應滿足13°沖擊試驗要求，試驗方法如圖8所示。將試驗車輪和輪胎總成安裝到試驗機上，車輪的軸線應與鉛直方向成(13±1)°角；沖錘在輪緣最高點上方(230±2)mm處，并與輪緣重疊(25±1)mm；然后釋放重錘，進行沖擊。沖擊結束后不能有可見裂紋穿透車輪中心部分的截面，車輪中心部分與輪輞不能分離，1 min內輪胎氣壓不能全部泄露。

圖8 車輪13°沖擊試驗示意圖Fig.8 Schematic diagram of 13 ° impact test of wheel

沖錘質量滿足下式：

m=0.6W+180

(8)

式中：m為沖錘質量(kg)；W為車輪最大靜載荷(kg)。

結合車輪型號，試驗參數確定如下：W=615 kg，輪胎充氣壓力為0.245 MPa。根據式(8)，則m=549 kg。

3.2 控制方程

車輪沖擊的有限元仿真分析，屬于材料非線性、幾何非線性和接觸非線性的問題，采用拉格朗日法描述物體的運動和變形，每個節點和整體都滿足質量、動量和能量守恒。在笛卡爾坐標系Ox1x2x3中，質量守恒方程、動量守恒方程和能量守恒方程如式(9)所示：

(9)

式中：ρ0(a)為初始時刻，點ai(i=1,2,3)處的物質密度；ρ(x)為經歷時間t后，點xj(a1,a2,a3,t)(j=1,2,3)處的物質密度，也記為ρ；vi為點xi處的速度；Xi為單位體積的體力；σij為應力場；u為單位質量內能；hi為熱通量矢量h的分量；Vij為應變率張量。

其中，物體在運動和變形過程中的應力邊界條件、位移邊界條件和接觸邊界條件如下式所示：

(10)

式中：σij為應力場；nj(j=1,2,3)為邊界面的外法線方向余弦；Ti(i=1,2,3)為面力載荷；xi為位置坐標；Di(t)為位移函數。

通過將以上邊界條件代入各節點進行運算可以得到每一個節點的運動規律和能量變化規律，即整個結構碰撞響應的特征關系。

本文采用LS-DYNA進行沖擊仿真，用罰函數法處理接觸問題，分別對單個部件和整體采用局部和整體沙漏控制。采用顯式中心差分算法，其穩定性決定于時間步長，積分時間步長滿足下式：

(11)

式中：ξ為系統阻尼比；ωmax為系統最大固有頻率；Ls為單元特征長度；c為物質中的聲速；ρ為物質密度；E為物質彈性模量。

3.3 材料模型

鎂、鋁合金在沖擊過程中受應變硬化和應變率硬化的影響較大，因此，需要設置考慮應變率效應的鎂、鋁合金材料模型。

AZ91D鎂合金和6061鋁合金試件按照GB/T 2975-1998進行取樣，并按照GB/T 228-2002進行靜態拉伸試驗，分別在0.003、0.01、0.1、1、10、25、100和1000 s-1應變率下測量AZ91D和6061的應力應變數據，結果如圖9所示。

圖9 車輪材料應力-應變實驗曲線Fig.9 Stress-strain experimental curves of wheel materials

輪胎分為胎面、兩胎側、胎體(Carcass)和內襯層(Inner liner)5個部分建模，胎體采用各向同性彈性材料，使用MAT1材料模型；胎面、兩胎側和內襯層采用各向同性超彈性材料，使用Yeoh材料模型。

Yeoh模型適合模擬炭黑填料天然橡膠的大變形行為，并且可以用簡單的單向拉伸試驗的數據去模擬其他變形的力學行為。Yeoh形式可以產生典型的S形的橡膠應力-應變曲線，其表達式如下：

(12)

式中：Ci0和Di均為待定材料模型參數；J為彈性體積比；I1為第一階應變不變量。

對于不可壓縮材料，Yeoh形式簡化為下式：

(13)

在小變形情況下，C10代表初始剪切模量；由于第2個系數C20為負，在中等變形時可反映材料的軟化現象；但由于第3個系數C30為正，在大變形情況下又可描述材料的硬化現象。

依據文獻[32]，胎面、兩胎側和內襯層的橡膠材料材料參數見表3。胎體的材料參數如下：密度為7.80×10-9t/mm3；彈性模量為2.07×5 MPa；泊松比為0.3。

表3 各橡膠材料的Yeoh模型參數Table 3 Parameters of Yeoh model for rubber materials

3.4 邊界條件

在Hypermesh中建立車輪13°沖擊試驗臺架的有限元模型，如圖10所示。

圖10 車輪13°沖擊試驗臺架有限元模型Fig.10 Finite element model of test bench in 13° impact of wheel

圖10中，臺架上、下支架用4個天然橡膠墊固連，并通過轉動臂連接。為了避免出現較大的沙漏和質量增加、甚至負體積或節點速度過高等錯誤，每個橡膠墊分別用一個彈簧單元來模擬橡膠的靜態變形特征和一個阻尼單元來模擬橡膠的動態阻尼特性。彈簧單元采用SDMAT1材料模型，k=326 N/mm；阻尼單元采用SDMAT2材料模型，c=500 N·s/mm。上、下支架和轉動臂的銷孔之間的轉動使用Revolute joint功能來實現。

在Hypermesh中建立車輪13°沖擊試驗的有限元模型，設置沖錘正對輻條和正對窗口兩種工況，如圖11所示。

圖11 車輪13°沖擊試驗有限元模型Fig.11 Finite element models of 13° impact test of wheel

輪輞和輪輻分別離散為邊長為4 mm和5 mm的四面體單元，輪胎、試驗臺架和沖錘分別離散為邊長為10 mm、30 mm和30 mm的四邊形和三角形混合殼單元。輪輞和輪輻之間的螺栓連接用RBE2模擬。共離散為519 762個單元，118 515個節點。

AZ91D鎂合金輪輞、6061鋁合金輪輻和A3鋼試驗臺架采用各向同性彈塑性材料，使用MAT24材料模型。A3鋼沖錘采用剛體材料，使用MAT20材料模型。

在輪胎和輪輞安裝貼合部位的接觸面間定義*Contact_shell_edge_to_surface_offset來模擬預緊力，該定義采用罰函數算法、約束平動與轉動、考慮失效。輪胎和輪輞中間定義*Airbag_simple_pressure_volume氣囊，初始氣壓為0.245 MPa。

為了節省計算時間，設置沖擊初始時刻沖錘在輪緣最高點上方2 mm處，則初始速度v=-2124 mm/s。沖錘配重0.549 t。整個模型都施加重力場，g=9800 mm/s2。約束下支架底板的所有自由度和沖錘的轉動自由度。根據式(11)，時間步長設為10-6s。模型計算結束時間設為0.05 s。

3.5 性能分析

將兩個工況下的有限元模型分別導入LS-DYNA進行計算，仿真計算后，質量增加了0.23%、能量變化了0.07%，均低于5%的要求。這證明了有限元模型的仿真結果是可信的。仿真計算中兩個有限元模型的能量變化曲線如圖12所示。

由圖12可知，沙漏能幾乎為零，總能量保持不變。隨著時間的增加，動能減小、內能增大，在45 ms時沖擊結束，之后各能量保持不變。

在兩種工況下，沖擊開始時輪胎內的氣壓有所降低，沖擊結束時趨于穩定，如圖13所示。

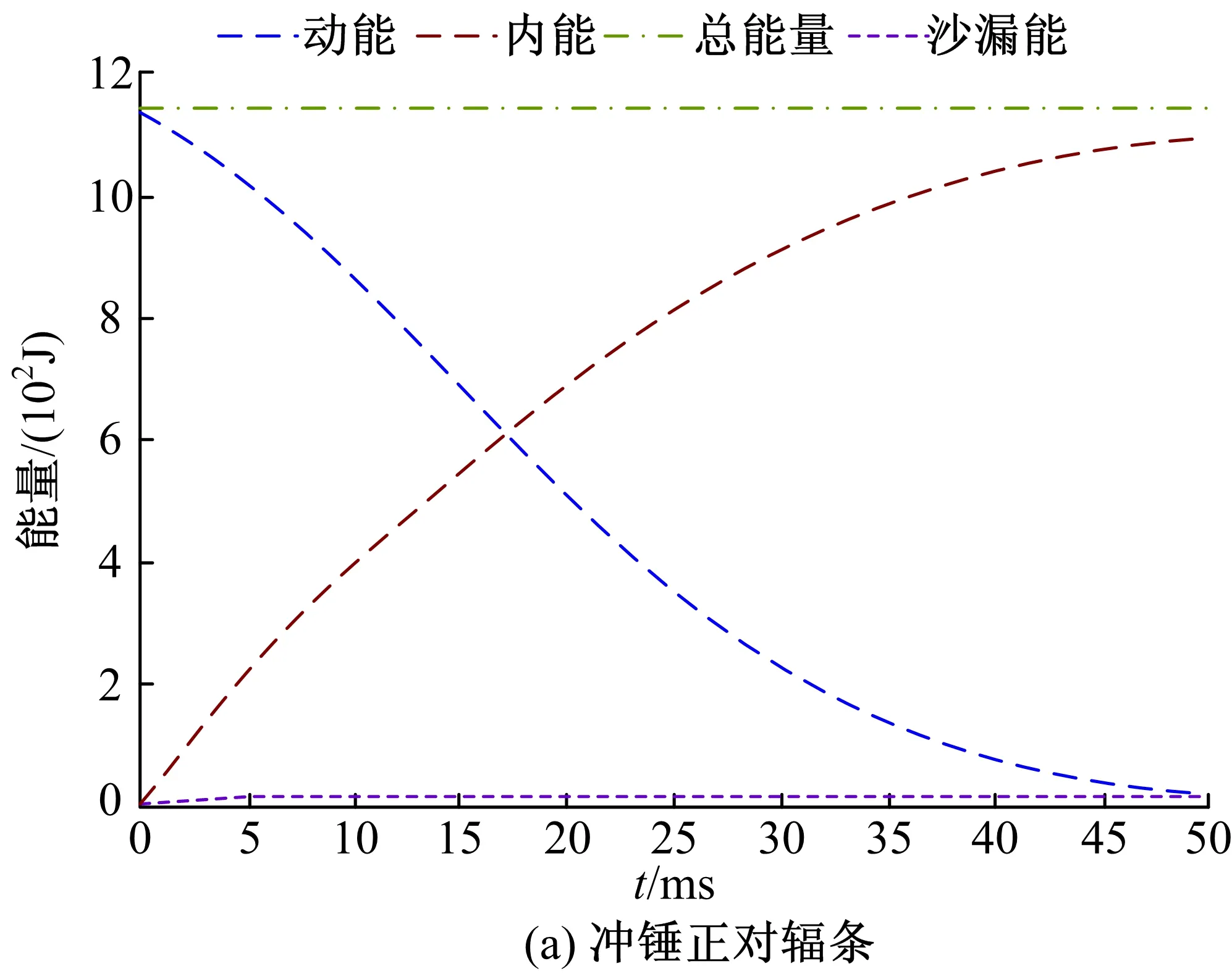
圖12 仿真分析中的能量變化曲線Fig. 12 Energy variation curves in simulation analysis

圖13 車輪13°沖擊中輪胎氣壓曲線Fig.13 Tirepressure curves in 13° impact test of wheel

車輪的最大應變發生在輪輻根部上表面，輪輞的應變很小。車輪在兩種工況下的應變云圖如圖14所示。

由圖14可知，沖錘正對輻條沖擊時，該輻條根部上表面的應變最大，為7.20%；沖錘正對窗口沖擊時，該窗口兩側輻條根部的應變最大，為6.53%。沖錘正對輻條沖擊時，車輪的受力變形更大、損傷更嚴重。所以，后文的多目標優化中，將以沖錘正對輻條沖擊時輪輻的應變為目標、沖錘正對窗口沖擊時輪輻的應變為約束。但是輪輻的應變小于8.7%，輪輞的應變遠小于8.1%，均不會產生裂紋；輪輻與輪輞連接處的應變也很小，不會發生輪輻與輪輞分離。車輪模型滿足13°沖擊試驗要求，并有進一步的優化空間。

圖14 車輪應變云圖Fig.14 Straincountours of wheel

6061鋁合金輪輻彈性變形極限的應變為0.28%，13°沖擊后應變超過0.28%的輪輻單元，如圖15所示。

圖15 應變大于0.28%的輪輻單元Fig.15 Disc elements of strain larger than 0.28%

由圖15可知，大于彈性極限應變的單元多集中在輪輻根部。輪輻根部的結構尺寸對車輪13°沖擊性能的影響很大，在多目標優化設計時，減小其他部位尺寸而增大輪輻根部尺寸能同時滿足車輪的輕量化和13°沖擊性能的提升。此外，在沖擊部位的輪輻和圓環交結處、圓環螺栓孔處也聚集了大于彈性極限應變的單元。

4 組裝式車輪多目標優化設計

4.1 車輪參數化建模

為了研究組裝式車輪結構與13°沖擊性能之間的關系，并對車輪進行多目標優化設計，需要建立參數化車輪模型[33,34]。

基于網格變形技術，采用DEP-MeshWorks軟件分別對沖錘正對輻條沖擊和正對窗口沖擊兩種工況下的車輪進行參數化，建立組裝式車輪的參數化模型，定義10個厚度變量和2個形狀變量(記為x1，x2，…，x12)，如圖16所示。表4給出了各設計變量的取值范圍。

圖16 車輪設計變量及參數化模型Fig.16 Design variables and parametric model of wheel表4 各設計變量及取值范圍Table 4 Designvariables and range of values

設計變量變量描述初始值下限上限x1/mm輪輻根部寬度增量0-55x2/mm輪輻頂部寬度增量0-44x3/mm輪輻根部厚度增量0-44x4/mm輪輻正面圓弧縮放系數10.81.2x5/mm輪輻背面圓弧縮放系數10.81.2x6/mm輪輻頂部厚度增量0-22x7/mm輪輻通槽寬度增量0-44x8/mm輪輻通槽長度增量0-44x9/mm輪轂厚度增量0-55x10/mm輪輻環厚度增量0-22x11/mm輪輞環厚度增量0-22x12/mm輪輞厚度增量0-11

4.2 近似模型

為了提高優化效率，使用近似模型進行多目標優化設計[35]。采用徑向基RBF網絡近似模型代替有限元計算來獲取各設計變量和各性能指標之間的關系[36,37]。在兩個有限元模型中，使用最優拉丁超立方設計方法分別采樣80個試驗點來擬合近似模型；另外采用Box-Behnken設計分別采樣10個試驗點來檢驗近似模型精度。通過決定系數R2檢驗近似模型的精度[38]，其表達式為

(14)

R2的值越接近1，則近似模型的擬合精度越高。各性能指標的決定系數R2值均大于92%，滿足近似模型擬合精度要求。部分性能指標的近似模型精度檢驗結果如圖17所示。

圖17 部分性能指標的近似模型精度Fig.17 Surrogate model accuracy of partialperformance indexes

4.3 多目標優化設計

綜合考慮車輪13°沖擊的性能指標，對組裝式車輪進行多目標優化設計，優化的數學模型為:

(15)

式中：m(x)為車輪質量(kg)；εsd(x)和εsr(x)分別為沖錘正對輻條沖擊時輪輻和輪輞的最大應變；εwd(x)和εwr(x)分別為沖錘正對窗口沖擊時輪輻和輪輞的最大應變；εd0和εr0分別為輪輻和輪輞的許用應變，εd0=8.7%，εr0=8.1%；x為設計變量，xL和xU分別為設計變量取值的下限和上限。

將13°沖擊性能指標計算軟件集成到多學科優化設計平臺Isight軟件中，建立基于徑向基RBF網絡近似模型和第二代非劣排序遺傳算法(NSGA-Ⅱ)的組裝式車輪多目標優化分析模型，如圖18所示。

圖18 車輪多目標優化分析模型Fig.18 Multi-objectiveoptimization andanalysis model of wheel

4.4 優化結果分析

經過8002次迭代，優化得到的Pareto前沿如圖19所示。

圖19 Pareto前沿Fig. 19 Pareto frontier

依據圖19，車輪質量和輪輻沖擊應變兩個目標函數是相互矛盾的，其中一個最優要以另一個最差為代價。本文優先考慮車輪的輕量化，沖擊性能屬于次要目標，因此要在滿足車輪13°沖擊性能的條件下盡量降低質量。在Pareto前沿中選取一個妥協解，如圖中綠點所示。優化前后各設計變量和各性能指標的對比分別如表5和表6所示。

表5 優化前、后設計變量取值Table 5 Values of design variables before and afteroptimization

表6 優化前、后各性能值對比Table 6 Values of performance indexes before and afteroptimization

5 結 論

(2)建立了車輪13°沖擊試驗的有限元模型，并檢驗了模型的可信性。使用了輪胎的Yeoh材料模型，基于不同應變率下AZ91D和6061的材料本構關系分別分析了沖錘正對輻條和正對窗口沖擊兩種工況下車輪的應變，其中沖錘正對輻條沖擊時車輪應變更大。

(3)大于輪輻彈性極限應變的單元多集中在輪輻根部。輪輻根部的結構尺寸對車輪13°沖擊性能的影響很大，減小其他部位尺寸而增大輪輻根部尺寸能同時滿足車輪的輕量化和13°沖擊性能的提升。

(4)基于網格變形技術建立了兩種工況下車輪的參數化模型，使用Isight軟件集成各工況的計算軟件并綜合運用DOE采樣、近似模型理論和NSGA-Ⅱ對車輪進行多目標優化設計，得到了Pareto前沿。在綜合考慮并滿足了車輪13°沖擊性能的條件下選取了一個妥協解，并對比分析了優化前、后車輪各性能指標的變化，結果表明：相對于同型鑄造鋁合金整體式車輪，本文設計的組裝式車輪減重30.65%。

(5)通過對車輪的聯合拓撲優化、13°沖擊性能的仿真分析和參數化建模，實現了一套基于車輪疲勞性能和13°沖擊性能的結構設計流程和優化方法，為車輪多目標優化設計提供了理論和技術依據。

[1] Hirano A. Study on wheel stiffness considering balance between driving stability and weight [C]∥SAE Paper，2015-01-1755

[2] Shang D, Liu X, Shan Y, et al. Research on the stamping residual stress of steel wheel disc and its effect on the fatigue life of wheel [J]. International Journal of Fatigue, 2016, 93: 173-183.

[3] Ballo F, Frizzi R, Mastinu G, et al. Lightweight design and construction of aluminum wheels [C]∥SAE Paper, 2016-01-1575.

[4] Oery T, Sankaran R T, Nesarikar A S. Simulation and test correlation of wheel radial fatigue test [C]∥SAE Paper, 2013-01-1198.

[5] Bends?e M P, Kikuchi N. Generating optimal topologies in structural design using a homogenization method [J]. Computer Methods in Applied Mechanics and Engineering, 1988, 71(2): 197-224.

[6] Jeong S H, Yoon G H, Takezawa A, et al. Development of a novel phase-field method for local stress-based shape and topology optimization [J]. Computers and Structures, 2014, 132(1): 84-98.

[7] Liu J, Ma Y. A survey of manufacturing oriented topology optimization methods [J]. Advances in Engineering Software, 2016, 100: 161-175.

[8] Deaton J D, Grandhi R V. A survey of structural and multidisciplinary continuum topology optimization: post 2000 [J]. Structural and Multidisciplinary Optimization, 2014, 49(1): 1-38.

[9] Sangree R, Carstensen J V, Gaynor A T, et al. Topology optimization as a teaching tool for undergraduate education in structural engineering [C]∥Structural Engineering Proceedings of the Structures Congress, Portland, OR，2015: 2632-2642.

[10] Zhang Z J, Jia H L, Sun J Y, et al. Application of topological optimization on aluminum alloy automobile wheel designing [J].Advanced Materials Research , 2012,562-564: 705-708.

[11] Hu J H,Liu X X, Sun H X, et al. Development and application of light-weight design of the aluminum alloy wheel [C]∥Applied Mechanics and Materials Trans Tech Publications, 2013, 310: 253-257.

[12] Xiao D, Zhang H, Liu X, et al. Novel steel wheel design based on multi-objective topology optimization [J]. Journal of Mechanical Science and Technology, 2014, 28(3): 1007-1016.

[13] 臧孟炎, 秦滔. 鋁合金車輪 13°沖擊試驗仿真分析[J]. 機械工程學報, 2010, 46(2): 83-87.

Zang Meng-yan, Qin Tao. Simulation analysis of car A-alloy wheel 13° impact test [J]. Journal of Mechanical Engineering, 2010, 46(2): 83-87.

[14] 尹冀, 朱平, 章斯亮. 考慮應變率效應的鋼制車輪沖擊仿真與試驗[J]. 上海交通大學學報, 2013, 47(6): 967-971.

Yin Ji, Zhu Ping, Zhang Si-liang. Simulation and experimental study of steel wheel impact test considering strain rate effect [J]. Journal of Shanghai Jiaotong University, 2013, 47(6): 967-971.

[15] Chang C L, Yang S H. Simulation of wheel impact test using finite element method [J]. Engineering Failure Analysis, 2009, 16(5): 1711-1719.

[16] 鄭玉卿, 劉建峰. 基于 Abaqus 顯式算法的鑄鋁車輪碰撞模擬[J]. 汽車工程, 2011, 33(2):152-155.

Zheng Yu-qing, Liu Jian-feng. Impact simulation of casting aluminum wheel using Abaqus/explicit [J]. Automotive Engineering, 2011, 33(2):152-155.

[17] Vinothkumar S, Srinivasan S, Nesarikar A K. Simulation and test correlation of wheel impact test [C]∥SAE Paper, 2011-28-0129.

[18] 閆勝昝, 童水光, 朱訓明. 輪胎充氣壓力對車輪應力分布影響的數值模擬[J]. 浙江大學學報:工學版, 2009, 43(3): 565-569.

Yan Sheng-zan, Tong Shui-guang, Zhu Xun-ming. Numerical simulation on influence of tire pressure to stress distribution in wheel [J]. Journal of Zhejiang University (Engineering Science), 2009, 43(3): 565-569.

[19] Tsai G C, Huang K Y. 13° impact test analysis of aluminum alloy wheel [C]∥Advanced Materials Research, Trans Tech Publications, 2013, 631: 925-931.

[20] 張響. 鋁合金車輪數字化仿真及工藝優化[D]. 浙江: 浙江大學材料與化學工程學院, 2008.

Zhang Xiang. Aluminum wheel digital simulation and process optimization [D]. Zhejiang: College of Materials and Chemical Engineering, Zhejiang University, 2008.

[21] Chauhan M R, Kotwal G, Majge A. Numerical simulation of tire and wheel assembly impact test using finite element method [C]∥SAE Paper, 2015-26-0186.

[22] 王寧, 杜林秀, 吳迪, 等. 超級鋼汽車車輪強度有限元分析[J]. 東北大學學報 ：自然科學版, 2006, 27(7): 779-781.

Wang Ning, Du Lin-xiu, Wu Di, et al. FEM analysis of strength of automotive wheels made from ultra-fine grain steel [J]. Journal of Northeastern University (Natural science), 2006, 27(7): 779-781.

[23] 暢世為, 張維剛. 復合材料車輪沖擊試驗仿真分析[J]. 汽車工程, 2010, 32(1): 65-68.

Chang Shi-wei, Zhang Wei-gang. A simulation analysis on the impact test of composite wheel [J]. Automotive Engineering, 2010, 32(1): 65-68.

[24] Tiwari D, Arora J, Khanger R. Study of parameters affecting the impact performance of an alloy wheel and noble approach followed to improve the impact performance [C]∥SAE Paper, 2015-01-1514.

[25] Shang R, Altenhof W, Hu H, et al. Kinetic energy compensation of tire absence in numerical modeling of wheel impact testing [C]∥SAE Paper, 2005-01-1825.

[26] Stearns J,Srivatsan T S, Prakash A, et al. Modeling the mechanical response of an aluminum alloy automotive rim [J]. Materials Science and Engineering A, 2004, 366(2): 262-268.

[27] Sah S K, Bawase M A, Saraf M R. Light-weight materials and their automotive applications [C]∥SAE Paper, 2014-28-0025.

[28] Ballo F, Mastinu G, Gobbi M. Lightweight design of a racing motorcycle wheel [C]∥SAE Paper, 2016-01-1576.

[29] Collet M,Bruggi M, Duysinx P. Topology optimization for minimum weight with compliance and simplified nominal stress constraints for fatigue resistance [J]. Structural and Multidisciplinary Optimization, 2016,55(3): 1-17.

[30] Bruggi M, Duysinx P. Topology optimization for minimum weight with compliance and stress constraints [J]. Structural and Multidisciplinary Optimization, 2012, 46(3): 369-384.

[31] Rozvany G I N. On symmetry and non-uniqueness in exact topology optimization [J]. Structural and Multidisciplinary Optimization, 2011, 43(3): 297-317.

[32] 李兵. 計及復雜胎面花紋的子午線輪胎結構有限元分析[D]. 合肥: 中國科學技術大學工程科學學院, 2008.

Li Bing. Finite element structural analysis for radial tires with complex tread patterns considered [D]. Hefei: School of Engineering Science, University of Science and Technology of China, 2008.

[33] Yi G, Kim N H. Identifying Boundaries of Topology Optimization Results using basic Parametric Features [M]. New York: Springer, 2016: 1-14.

[34] Hahn Y, Cofer J I. Study of parametric and non-parametric optimization of a rotor-bearing system[C]∥Turbine Technical Conference and Exposition, American Society of Mechanical Engineers, 2014: V07AT28A001-V07AT28A001.

[35] Leifsson L, Hermannsson E, Koziel S. Optimal shape design of multi-element trawl-doors using local surrogate models [J]. Journal of Computational Science, 2015, 10: 55-62.

[36] Golzari A, Sefat M H, Jamshidi S. Development of an adaptive surrogate model for production optimization [J]. Journal of Petroleum Science and Engineering, 2015, 133: 677-688.

[37] Pan I, Das S. Kriging based surrogate modeling for fractional order control of microgrids [J]. IEEE Transactions on Smart Grid, 2015, 6(1): 36-44.

[38] Mehmani A, Chowdhury S, Messac A. Predictive quantification of surrogate model fidelity based on modal variations with sample density [J]. Structural and Multidisciplinary Optimization, 2015, 52(2): 353-373.