基于等效晃動模型的液罐車防側翻控制策略

趙偉強，封 冉，宗長富

(吉林大學 汽車仿真與控制國家重點實驗室，長春 130022)

0 引 言

隨著中國道路交通的迅速發展，利用液罐車運輸液體危化品所占的比例越來越大。液罐車具有噸位大、質心高的特點，同時由于罐內液體的流動特性，當液罐車在彎道行駛或緊急避障時，車輛狀態的改變會使液體對罐壁產生沖擊，從而進一步降低液罐車的行駛穩定性，易使其發生側翻事故，進而導致危化品的泄漏、燃燒甚至爆炸，不但造成大量人員傷亡、財產損失并且嚴重污染環境。

目前，針對液罐車的研究主要集中于罐內液體晃動的動力學機理分析、罐體結構的優化等。文獻[1]運用流體體積(VOF)法對非滿載液罐車在極限工況時罐內液體晃動動力學特性進行數值模擬，并分析了液罐內防波板數量、結構以及充液比等影響因素。文獻[2，3]研究了橢圓形截面液罐車罐體幾何尺寸對整車側傾穩定性的影響，得出液罐車所受罐內液體沖擊力及力矩最小時的長軸與短軸比例值及具體尺寸。液罐結構優化能在一定程度上提高其穩定性，但其效果遠不如對車輛應用主動控制策略[4-7]。

液罐車動力學模型需兼顧準確性及計算速度，液體晃動簡化模型主要包括準靜態模型以及等效機械模型[8-10]，其中準靜態模型中不包含液體的晃動，然而等效機械模型既考慮了車輛側傾時液體質心偏移產生的側傾力矩，又考慮了液體對罐體壁面的沖擊效應[11-15]。

針對目前提高液罐車穩定性的方法以及液罐車模型兩方面的不足，本文建立了液罐車等效晃動動力學模型，并提出基于差動制動的液罐車防側翻控制策略；通過Trucksim/Simulink聯合仿真，驗證了液體晃動對車輛運動的影響以及防側翻控制策略的有效性。

1 液罐車動力學模型

本文的研究對象為單車式液罐車且罐體為矩形，裝載貨物為煤油，車輛側視圖、俯視圖及后視圖如圖1～圖3所示。

圖1 液罐車側視圖Fig.1 Left view of tank truck

圖2 液罐車俯視圖Fig.2 Top view of tank truck

圖3 液罐車后視圖Fig.3 Rear view of tank truck

在部分充液情況下，液罐內液體在車輛運動的激勵下將產生對液罐壁面的沖擊力，進而影響車輛的運動狀態，沖擊力的大小可用來表征液體晃動的劇烈程度。

1.1 液罐車車體部分動力學模型

本文采用3自由車輛模型，包括車輛側向、橫擺和側傾運動，在建立動力學模型時，需要對實際車輛作如下假設：①模型以前輪轉角作為輸入；②汽車在水平路面行駛，忽略車輛的垂直運動；③不考慮車輛的俯仰運動；④忽略空氣動力的作用；⑤忽略左、右輪胎由于載荷的變化引起輪胎特性的變化以及輪胎回正力矩作用。

根據達朗伯原理，可對液罐車車體部分建立動力學平衡方程。

沿y軸力平衡式：

(1)

繞z軸橫擺力矩平衡式：

(2)

繞x軸側傾力矩平衡式：

(3)

式中：Fyl表示液體晃動對罐壁的沖擊力；hFyl為沖擊力作用點到側傾軸線的距離，由雙向耦合關系知，兩值可由液體晃動模型求解得到。

1.2 液體晃動等效模型

目前，針對儲液罐內液體晃動現象的沖擊動力學研究方法主要有：數值模擬法、機械動力學等效法和物理試驗法。其中數值模擬法求解過程復雜，物理實驗法試驗要求高、危險性較大，為保證模型計算的實時性，通常將液體晃動問題等效為機械模型。由于單擺模型可有效反映液體在橫向激勵中的晃動特性，因此本文采用單擺模型描述罐內液體運動。

液體晃動單擺模型示意圖如圖4所示，其中液體質量分為固定質量mo及等效單擺質量mp兩部分，固定質量質心位于距罐底部ho處，單擺質量位于距罐底部hp處。

圖4 等效單擺模型示意圖Fig.4 Equivalent pendulum model

具體計算公式如下：

ml=ρhsed

(4)

(5)

mo=ml-mp

(6)

(7)

(8)

式中：hs為罐內液體深度；e、d分別為罐體的長與寬。

單擺模型可近似看做系于液罐中心處，即所有的旋轉被認為在該點附近發生，因此，罐體的中心和單擺質量之間的距離可以被認為是等效擺長lp。液體的固有頻率與等效擺長有關，計算公式如下：

(9)

單擺模型的動力學方程和橫向激勵產生的晃動力以及液體晃動對罐底的力矩計算方程如下：

(10)

(11)

M=Fylhp+mpglpθ

(12)

式中：θ為等效擺角；cl為液體等效阻尼系數。

2 防側翻控制策略

2.1 預警指標

判定車輛是否會發生側翻，目前應用比較廣泛的是橫向載荷轉移率法，橫向載荷轉移率(LTR)是指車輛兩側車輪上的垂直載荷之差與垂直載荷之和的比值，具體表達式如下：

(13)

式中：Fzl和Fzr分別為車輛左、右車輪上的垂直載荷。

在極限工況下，若一側車輪抬起脫離地面，此時LTR為-1或1，因而該值可反映車輛的側傾穩定性。由于左、右車輪垂直載荷不易直接測量，所以本文采用其等效表達式：

(14)

式中：C、K分別為懸架阻尼與剛度值；φ為車輛側傾角；T為車輛輪距。

2.2 制動輪缸壓力決策

本文基于差動制動設計防側翻控制策略，當預警模塊檢測到車輛將要側翻時，激活防側翻控制模塊，根據實際側傾角與理論側傾角的偏差求得補償橫擺力矩值，進而求得制動輪輪缸壓力值，從而防止車輛側翻。本文采用PID算法，補償橫擺力矩計算框圖如圖5所示。

φt為經3自由度液罐車模型計算得到的理想側傾角值，φa為來自Trucksim的實際車輛側傾角，eφ為二者的偏差值。補償橫擺力矩具體計算公式如下：

(15)

式中：kP為比例系數；TI是積分時間常數；TD是微分時間常數。

圖5 補償橫擺力矩計算框圖Fig.5 Calculation of additional yaw moment

能夠提供有效補償橫擺力矩的車輪有前輪和后外輪，但每個車輪效率不同，本文選擇車輛前輪作為制動輪。LTR數值可以反映車輛的轉向狀態，現制定制動車輪決策規則如下：若LTR∈[-1,0)，表示車輛向左側轉彎，此時選擇右前輪作為制動輪；同理，若LTR∈(0,1]，選擇左前輪作為制動輪。

制動輪缸壓力計算公式如下：

(16)

式中：ΔP定義為輪缸所需壓力；ΔMφ定義為根據側翻控制策略計算得出的附加橫擺力矩；Rw為車輪半徑；Sc為制動氣室有效作用半徑；Rc為制動器的有效作用半徑；L為決策車輪到車輛質心位置的距離。

3 仿真分析

本文中，首先比較相同工況下，車輛在裝載等質量的液體貨物與固體貨物時的運動狀態，以確認液體晃動對車輛側傾穩定性的影響。其次，當發現液罐車具有側翻危險時，對車輛進行差動制動主動防側翻控制，通過比較控制前、后的液罐車狀態值來證明防側翻控制策略的有效性。

3.1 液體晃動對車輛運動狀態的影響

為確認液體晃動對車輛響應的影響，本文選擇階躍工況進行仿真分析，比較了當車速分別為40 km/h與70 km/h時，裝載相同質量的固體貨物與液體貨物的車輛側向加速度、橫擺角速度以及側傾角。

階躍轉向的方向盤轉角為180°，轉角增大時間為0.66 s，如圖6所示。

由圖7～圖9可知，在低速行駛時，由于罐內液體的晃動，液罐車的側向加速度、橫擺角速度、給定階躍工況下，車速為40 km/h時的仿真曲線如圖7所示。

圖6 方向盤階躍轉角Fig.6 Step input of steering wheel angle

圖7 側向加速度時間歷程Fig.7 Lateral acceleration

圖8 橫擺角速度時間歷程Fig.8 Yaw rate

圖9 側傾角時間歷程Fig.9 Roll angle

側傾角明顯大于裝載等質量固體貨物車輛的對應值，即液罐車穩定性明顯較低。

相同階躍工況下，當車輛速度均達到70 km/h時，仿真結果如圖10所示，裝載固體貨物的車輛側傾角保持在3°以內，而液罐車側傾角在2.5 s左右達到76°，即液罐車發生側翻。

圖10 70 km/h時側傾角Fig.10 Roll angle under 70 km/h

3.2 防側翻控制

為證明防側翻控制策略的有效性，針對上述階躍工況下，車速為70 km/h的液罐車進行防側翻控制。仿真結果如圖11所示，在4 s左右液罐車側傾角降至2.3°，隨后保持穩定，即在本文控制策略作用下車輛未發生側翻。

圖11 階躍工況有、無控制策略時側傾角比較Fig.11 Roll angle comparison in step condition

液罐車在50 km/h、魚鉤工況下方向盤轉角為±294°，轉角增大時間為0.4 s，如圖12所示。此外，本文還比較了在50 km/h、魚鉤工況下有無控制時的側傾角、側向加速度、液體晃動力，分別如圖13～圖15所示。

圖13、圖14表明，若不采取任何安全措施，液罐車在3.5 s左右發生側翻；然而，由圖15可知，在主動防側翻控制策略作用下，液體晃動力可從最大峰值17 kN降低至3.5 kN，并最終維持穩定，液罐車側傾角及側向加速度可保持在安全范圍內，即該策略有效地提高了液罐車的側傾穩定性。

圖12 方向盤轉角Fig.12 Steering wheel angle in fishhook condition

圖13 魚鉤工況時側傾角Fig.13 Roll angle in fishhook condition

圖14 魚鉤工況時側向加速度Fig.14 Lateral acceleration in fishhook condition

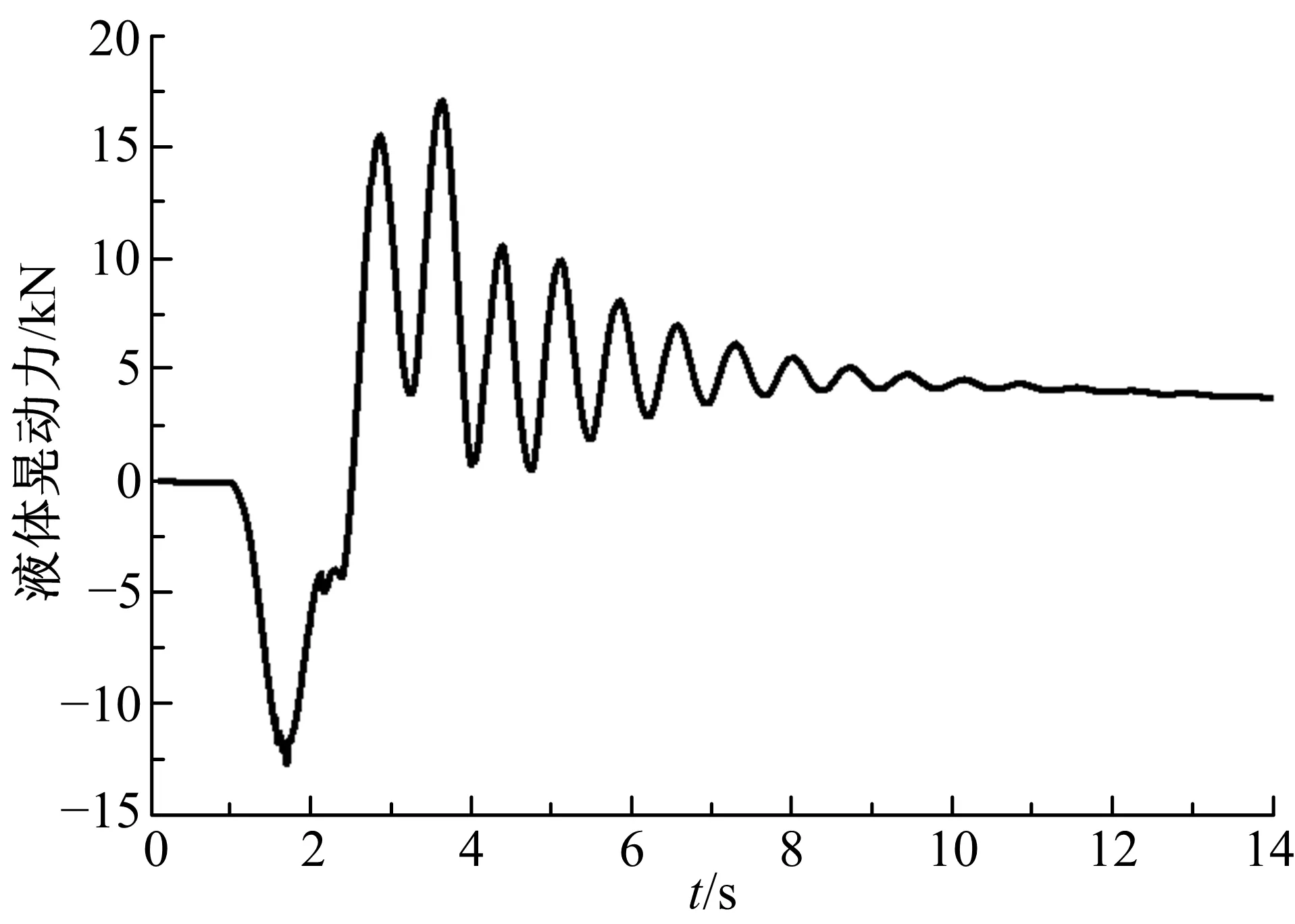
圖15 魚鉤工況時液體晃動力Fig.15 Sloshing force in fishhook condition

4 結束語

本文基于等效晃動模型對液罐車防側翻控制策略進行了研究。利用等效單擺模型模擬矩形液罐內液體的橫向晃動，并將該模型與3自由度車輛模型集成，建立了液罐車等效晃動動力學模型；驗證了階躍轉向工況下，液罐內液體晃動對車輛側向穩定性的影響；選取橫向載荷轉移率為側翻指標并利用差動制動方法，驗證了本文防側翻控制策略在階躍工況及魚鉤工況下的有效性。本文方法對于提高液罐車行駛穩定性，減少側翻事故具有一定的理論意義。

[1] 趙樹恩，趙靈鶴. 汽車罐車橫向運動液體晃動動力學特性模擬[J]. 應用數學和力學，2014，35(11)：1259-1270.

Zhao Shu-en,Zhao Ling-he.Dynamic Simulation of liquid sloshing characteristics for tank trucks in lateral movement [J]. Appllied Mathematics and Mechanics,2014,3(11):1259-1270.

[2] 于迪，李顯生，劉宏飛，等. 非滿載液罐車側傾穩定性模型研究[J]. 湖南大學學報：自然科學版，2016，43(8)：40-44.

Yu Di, Li Xian-sheng, Liu Hong-fei，et al. Research on roll stability model of partially-filled tankers [J]. Journal of Hunan University (Natural Sciences), 2016, 43(8): 40-44.

[3] 李顯生，于迪，張海景. 基于遺傳算法的液罐車側傾穩定性模型[J]. 中國公路學報，2015，28(7)：115-120.

Li Xian-sheng, Yu Di, Zhang-hai Jing. Roll stability model of tank truck based on genetic algorithm [J]. China Journal of Highway and Transport, 2015, 28(7):115-120.

[4] Avesta Goodarzi. Integrated yaw and roll moments control of articulated vehicles [C]∥SAE Paper, 2009-01-2874.

[5] Yoon Jang-yeol, Kim Dong-shin. Design of a rollover index-based vehicle stability control scheme [J]. Vehicle System Dynamics, 2007, 45(5): 459-475.

[6] 李顯生，鄭雪蓮，劉宏飛. 非滿載罐式半掛汽車列車側傾穩定性評價改進算法[J]. 吉林大學學報:工學版，2012，42(5):1089-1094.

Li Xian-sheng,Zheng Xue-lian, Liu Hong-fei. Improved algorithm on roll stability evaluation of partially filled tractor-tank semitrailer [J]. Journal of Jilin University (Engineering and Technology Edition), 2012, 42(5): 1089-1094.

[7] Acarman T, Ozguner U. Rollover prevention for heavy trucks using frequency shaped sliding mode control [J]. Vehicle System Dynamics, 2006, 44(10): 737-762.

[8] 胡曉明，李萬莉，孫麗，等. 液體晃動降低半掛液罐車行駛穩定性[J]. 農業工程學報，2013，29(6)：49-58.

Hu Xiao-ming, Li Wan-li, Sun Li, et al. Liquid sloshing reduces driving stability of semi-trailer liquid tank [J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(6): 49-58.

[9] 岳寶增，祝樂梅，于丹. 儲液罐動力學與控制研究進展[J]. 力學進展，2011，41(1)：79-91.

Yue Bao-zeng, Zhu Le-mei, Yu Dan. Recent advances in liquid-filied tank dynamics and control [J]. Advances in Mechanics, 2011, 41(1): 79-91.

[10] Mohammed B,Zu J W. Tractor-semitrailer model for vehicles carrying liquids [J]. Vehicle System Dynamics, 2006, 44(11): 871-885.

[11] 鄭雪蓮，李顯生，任園園,等. 非滿載罐體液體沖擊等效機械模型參數確定[J]. 湖南大學學報:自然科學版，2013，40(6):53-58.

Zheng Xue-lian, Li Xian-sheng, Ren Yuan-yuan, et al. Parameter values of equivalent mechanical model for liquid sloshing in partially-filled tanks [J]. Journal of Human University (Natural Sciences), 2013, 40(6):53-58.

[12] Chandrasekharan S, Guenther D A, Heydinger G J, et al. Development of a roll stability control model for a tractor vehicle [J]. SAE International Journal of Passenger Cars-Mechanical Systems, 2009, 2(1): 670-679.

[13] 胡曉明，李萬莉，趙志國,等. 液罐車罐體內液體橫向晃動研究[J]. 應用力學學報，2013，30(5)：641-646.

Hu Xiao-ming, Li Wan-li, Zhao Zhi-guo, et al. Horizontal fluid sloshing analysis in the body of tank truck [J]. Chinese Journal of Applied Mechanics, 2013, 30(5): 641-646.

[14] Lu Jian-bo, Messih David. An enhancement to an electronic stability control system to include a rollover control function [C]∥ SAE Paper, 2007-01-0809.

[15] 鄭雪蓮，李顯生，任園園,等. 瞬時液體沖擊對汽車罐車側傾穩定性的影響[J]. 吉林大學學報:工學版，2014，44(3)：625-630.

Zheng Xue-lian, Li-Xian-sheng, Ren Yuan-yuan, et al. Rollover stability analysis of tank vehicle impacted by transient liquid sloshing [J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(3): 625-630.