伯努利雙紐線右半有界區域內解析函數的優化性質

湯 獲，馬麗娜，牛瀟萌

（赤峰學院 數學與統計學院；赤峰學院 應用數學研究所，內蒙古 赤峰 024000）

1 引言

設C表示復平面,A表示在單位圓盤U={z∈C:|z|＜1}內解析且形如的函數類.

1967年,Macgregor[1]給出了優化的定義.

定義1設函數f和g在U內解析.若存在U內的解析函數 φ(z),使得 |φ(z)|≤1 和 f(z)=φ(z)g(z)(z∈U),則稱函數f在U內優于g,記作f(z)?g(z)(z∈U).

1970年,Roberston[2]引入了擬從屬的概念.

定義2設函數f和g在U內解析.若存在U內的解析函數φ(z),使得在 U 內解析且 |φ(z)|≤1 和 |ω(z)|≤|z|＜1(z∈U),滿足 f(z)=φ(z)g(ω(z))(z∈U),則稱函數f在U內擬從屬于g,記作f(z)?qg(z)(z∈U).我們注意到，當 φ(z)=1 時，f(z)=g(ω(z))(z∈U),此時稱函數f在U內從屬于g,記作f(z)?g(z)(z∈U)[3];當ω(z)=z時,擬從屬關系即為上述優化關系.因此,從屬關系和優化關系都是擬從屬關系的特殊情形.

1996年,Sokol和Stankiewicz[4]引入了伯努利雙紐線右半有界區域內的解析函數類BR*,討論了其凸半徑問題.

定義3設函數f∈A,則f屬于伯努利雙紐線右半有界區域內的函數類BR*當且僅當

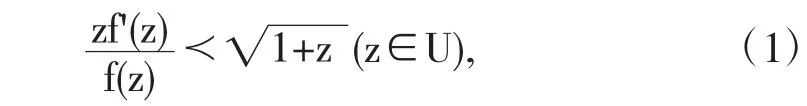
近年來,許多中外學者對由各種算子定義的不同單（多）葉解析函數類的優化問題做了大量研究,得到許多漂亮的結果[5-8].受上述工作的啟發,本文主要研究伯努利雙紐線右半有界區域內解析函數類BR*的優化性質,所得結果擴充了單復變幾何函數論中的優化理論.

圖1

2 定理及其證明

定理設函數f∈A和g∈BR*.若在U內f(z)優于 g(z),即 f(z)?g(z)(z∈U),則對 |z|≤r1,有 |f'(z)|≤|g'(z)|,其中r1是方程

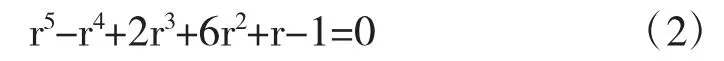
在區間(0,1)內的最小正根.

證明由于g∈BR*,故由從屬關系和（1）式,可得

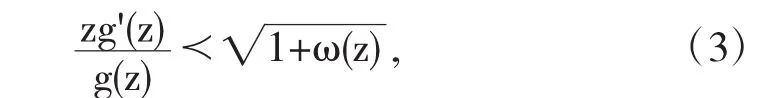
其中ω(z)=c1z+c2z2+…∈P,P表示在U內有界且滿足條件

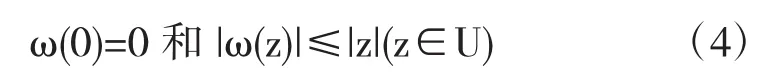
的解析函數類[9].

根據（3）式和（4）式,不難得到

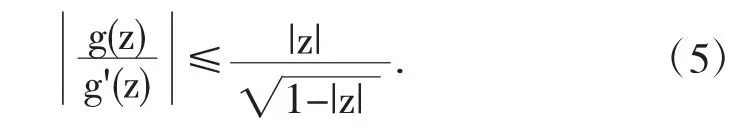
又f(z)?g(z),則由定義1可知

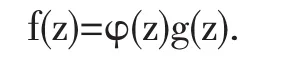
對上式兩邊關于z求導,可得

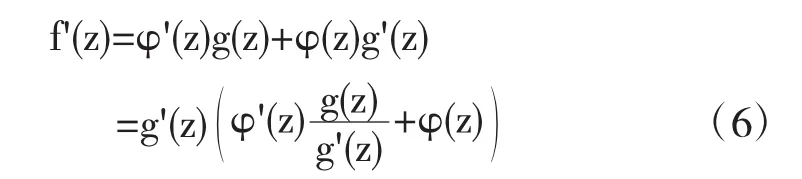
又注意到φ(z)∈P滿足不等式

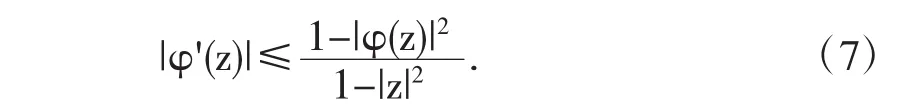
故將（5）式和（7）式代入（6）式,有

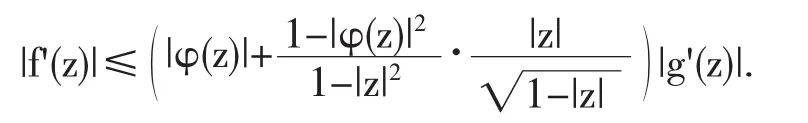
若取 |z|=r和 |φ(z)|=ρ(0≤ρ≤1),則上式可變為

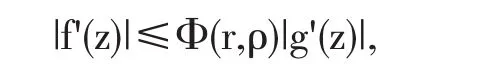
其中

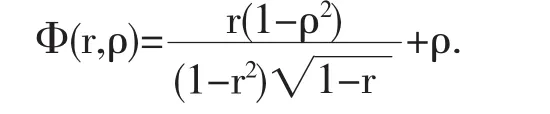
要確定r1,我們只需取

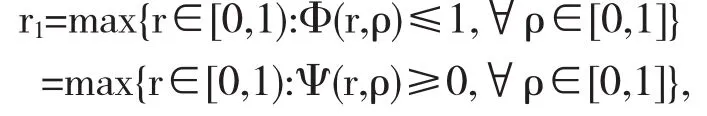
其中

顯然,當 ρ=1 時,Ψ(r,ρ)取得最小值, 即

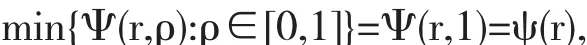
又因為函數 ψ(r)在(0,1)上連續,且 ψ(0)=1＞0,ψ(1)=-2＜0,故存在 r1,使得當 r∈[0,r1]時 ψ(r)≥0 成立,其中r1為方程（2）在區間(0,1)內的最小正根.定理得證.

〔1〕MacGregorT H.Majorization byunivalent functions[J].Duke Math J,1967,34：95-102.

〔2〕Roberston M S.Quasi-subordination and coefficient conjectures[J].Bull Amer Math Soc,1970,76：1-9.

〔3〕Srivastava H M,Owa S.Current Topics in Analytic Function Theory[M].World Scientific Publishing Company,Singapore,New Jersey,London,and Hong Kong,1992.

〔4〕Sokol J,Stankiewicz J.Radius of convexity of some subclasses of strongly starlike functions[J].Zesz Nauk Politech Rzeszowskiej Mat,1996,19：101-105.

〔5〕TangHuo,DengGuantie,LiShuhai.Majorization properties for certain classes of analytic functions involving a generalized differential operator[J].Journal of Mathematical Research with Applications,2013,33(5)：578-586.

〔6〕Li Shuhai,Tang Huo,Ao En.Majorization properties for certain new classes of analytic functions using the Salagean operator[J].J Inequal Appl,2013,2013：86.

〔7〕TangHuo,LiShuhai,DengGuantie.Majorization properties for a new subclass of -spiral functions of order [J].Mathematica Slovaca,2014,64(1)：39-50.

〔8〕Tang Huo,Aouf A K,Deng Guantie.Majorization problemsfor certain subclassesof meromorphic multivalentfunctionsassociated with the Liu-Srivastava operator[J].Filomat,2015,29(4)：763-772.

〔9〕Goodman A W.UnivalentFunctions[M].Mariner Publishing Company,Tampa,Florida,1983.

〔10〕Nehari Z.Conformal Mapping[M].Mac-Graw-HillBook Company,New York,Toronto and London,1955.