基于鏈路動態變化的產業網絡預測模型研究

王 斌王文平費為銀

(1.安徽工程大學數理學院,安徽蕪湖241000；2.東南大學經濟管理學院,江蘇南京211189)

1 引 言

經濟投入產出系統能夠被構建成產業網絡,節點表示系統中的各個產業或企業,鏈路表示相互之間的物質、副產品和能量的循環流動.網絡分析方法能夠探討產業網絡的結構和性質[1],能夠測量網絡中各個節點之間的交流,而且能夠解釋相互之間的影響和信息流動[2-4],因而它是分析經濟投入產出系統的一個有力工具.目前,產業網絡的構建主要基于投入產出表所反映的信息,并據此研究產業網絡結構特征及其演化,為產業結構的優化、以及產業的轉型升級提供合理的政策建議.如文獻[5—10]從整體的角度,以某個年份的投入產出表為基礎,研究產業網絡的無標度性、冪律分布和最大關聯樹等基本特征.文獻[11—15]從個體的角度,以幾個年份的投入產出表為基礎,研究產業網絡內的主導產業,如何在國家產業結構調整和優化升級過程中發揮各自的優勢和作用,以及探討產業網絡的演化,分析集群網絡之間的互動及部門角色的變動問題.可見,投入產出表對于研究產業網絡是多么的重要.但從時間維度看,基于投入產出表之上的產業網絡,只是研究了某些年份的產業網絡結構特征,而沒能克服借助靜態、歷史的數據研究產業網絡的局限.再從現實情況看,囿于編制投入產出表需要消耗大量的人力和物力,中國的投入產出表只是每五年編制一次,且表的公布年份距編表年份至少也會有2年～3年.較長的編表周期導致投入產出表注定是一種歷史數據,那么分析以該表為基礎的產業網絡,對于經濟結構變化較大的轉型經濟體來說,數年的滯后可能會影響研究結果的正確性.因此,及時、準確地預測產業網絡具有重要的意義.

若能克服投入產出表跨度大,不能及時、準確反映產業網絡結構變化的缺點,使得產業網絡的預測變得便捷可行,則能依據若干個年份的投入產出表,對產業網絡進行及時、動態的分析.事實上,隨著時間的演化,產業網絡中原有的鏈路可能消失或產生新的鏈路,從而表現出了較強的動態性和復雜性,處理如此問題選擇社會網絡分析法(SNA)十分適宜[16],鏈路預測又是網絡分析法中的重要任務之一.鏈路預測是指,依據已知的網絡結構等信息,預測網絡中尚未鏈接的兩個節點之間將來產生鏈接可能性的大小,該理論已經被廣泛應用于各種網絡分析當中[17-19].因此,鏈路預測是盡可能的推斷出兩個節點之間鏈接存在的可能性,具有重要的理論和實際意義.

在真實的網絡中,相比于用實驗結果去推斷兩個節點之間是否有相互作用關系,利用鏈路預測去預估節點將來的行為,或者識別兩個節點之間未來的鏈接,成本更為低廉.例如,在新陳代謝網絡與蛋白質相互作用網絡中,需要通過大量實驗結果推斷節點之間是否存在相互作用關系[20],高額的實驗成本自然不可避免.降低實驗成本,并且不失準確地推斷結論的理想方法,是針對這些網絡的結構特性、設計出一套足夠精確的鏈路預測算法,然后實驗在預測結果的指導下進行.已經有許多學者研究了鏈路預測的問題,這些研究主要是基于當前網絡的結構性質,預測任意兩個節點之間將來發生鏈接的概率,且研究的科學領域眾多.例如,Goldberg等[21]利用蛋白質網絡的局部集聚性,預測了缺失的鏈接；Manning等[22]構建了一個信息檢索網絡,節點代表關鍵詞或分類文件,通過預測兩者之間的關系,區分了未經辨識的文件.圖書推薦網絡是鏈路預測的另一個事例,Chen等[23]在用戶和書目之間建立了許多圖論測度,以期向用戶做圖書推薦.此系統是一個用戶—圖書的二部網絡,鏈路表示用戶對某種圖書的偏好.鏈路預測也可以被用于分析演化網絡,例如,Zhou等[24]利用鏈路預測理論分析了互聯網將來的形狀；Juszczyszyn等[25]利用馬爾科夫鏈構建了一個鏈路預測模型,分析了大學郵箱網絡的子圖結構隨時間的演化情況.解決鏈路預測問題一個最簡單的方法是所謂的得分算法,其中基于相似性的得分預測算法能夠得到很好的預測結果,并且網絡的拓撲結構性質能夠幫助選擇合適的相似性指標[26,27].隨后,學者們又考慮了加權網絡上的鏈路預測問題,發現含權指標的得分預測效果要好于無權的預測方法[28].這些研究都充分體現了得分預測算法的簡潔性,并且得分預測方法很容易和其他的方法相結合.例如,Aaron等[29]應用層級結構知識預測了丟失的鏈接,其中層級結構可以解釋許多網絡所表現出的右偏態度分布、高集聚系數和最短路徑長度性質.Chungmok等[30]從網絡度分布的角度,用數學規劃方法預測了網絡將來的結構,其中,預測問題被轉化為整數規劃問題,這樣做的目的是以便最大化鏈路預測得分總和.Chen等[31]構建了一個快速的相似性鏈路預測算法,并以真實的世界網絡進行了實證分析,結果表明新的算法比其他算法速度更快,而且精度更高.總之,學者們提出了諸多方法去解決鏈路預測問題,這些方法主要以測量節點之間相似性為基礎.其中目前應用最廣泛的測量方法、即相似性預測算法有結構等價指標CN、資源分配指標RA、約旦系數指標JC和阿達米克—亞達指標AA[32-34].

但是,以上的研究較少涉及到產業網絡的鏈路預測問題,并且隨著時間的演化,產業網絡中原有的鏈路可能消失或產生新的鏈路.相似性鏈路預測算法,雖然可以根據當前的產業網絡,預測任意兩個產業將來發生鏈接的概率.但是,產業網絡的拓撲結構隨時間而變化,產生了大量涉及節點和鏈路的動態信息,若能在鏈路預測的算法當中體現出這些有用信息,則預測的精度會有進一步的提高.為了檢驗這個設想,本文以中國2005年、2007年、2010年和2012年的四個投入產出表為研究對象,首先構建四個有權重的產業網絡,然后基于權重網絡提出一種新的鏈路預測算法,建立基于鏈路動態變化的產業網絡預測得分算法,識別兩個產業之間建立鏈接的可能性大小.與相似性預測算法相比,這種新的算法不僅考慮兩個節點之間的相似性程度,受到共同鄰居節點的影響(本文用控制變量α表示),而且考慮在前期網絡和當前網絡中,鏈路權重的變化程度(本文用變化率r表示).在考慮了變化程度的基礎上,又進一步考慮了鏈路權重變化的方向,即權重的增減情況(本文分別用三個參數δ,η,θ表示).此外,為了測試本文提出的預測算法性能優劣,又進一步引入了目前應用最廣泛的相似性鏈路預測算法作為對比,結果顯示本文提出的鏈路預測模型的預測精度更高.因此,在預測產業網絡的鏈路時,不僅要考慮當前產業網絡的鏈路情況,還要充分考慮產業網絡中鏈路的動態變化信息,這樣得出的結果才會更加準確可靠.

2 基于鏈路動態變化的產業網絡預測模型

產業網絡具有動態的演化結構,這些結構隨時間的演化而變化,新的節點不斷產生,新的鏈路不斷形成,以及其上的權重不斷改變,使得產業網絡結構具有動態性.針對產業網絡中鏈路動態變化的特性,并考慮到兩個節點鄰居的得分情況,本文提出的預測算法,在權重的特定比例上定義預測得分的增加或減少.

2.1 產業網絡模型的構建

本文旨在研究產業網絡中的鏈路預測方法,因此,首先討論如何構建產業網絡,而投入產出表是構建產業網絡的基礎,且能準確表達各個產業部門在生產與分配領域的經濟聯系.本文分析的投入產出表,是以直接消耗系數為元素所構成的矩陣.記A=(aij)n×n為直接消耗系數矩陣,其中aij,i,j=1,2,...,n為直接消耗系數,且aij∈[0,1].直接消耗系數反映了產業部門生產一個單位的總產品所需要消耗其他部門產品的比例,它是一個無量綱的數值,恒在[0,1]區間變化,因此不會發生隨著經濟的增長其絕對值隨之增加的情況,并且本文是根據歷年的投入產出情況,預測任意兩個產業部門之間未來的鏈接情況,而直接消耗系數既可以反映兩個部門之間有無聯系,又可以反映出聯系的緊密程度,其比值越接近于1,聯系越緊密；反之越稀疏.以直接消耗系數為鏈路,產業為節點構建的產業網絡考慮的是任意兩個產業部門之間的鏈接情況,與方向無關,因此本文研究無向網絡.同時,考慮到鏈接的重要性,借鑒劉剛等[6]的處理方法,僅將兩鏈接量作均值處理,再將所有產業對鏈接量的均值設為閾值,閾值以上的值定為有效鏈接.

2.2 產業網絡的結構指標

1)平均度

網絡的平均度定義為節點度數中心性的平均值,節點i的度數中心性表示與其相連邊的個數ki,其表達式為

其中Γ表示與節點i直接相連的節點組成的集合,亦稱為節點i的鄰居節點集.eij=1時表示節點i與j存在連邊,否則eij=0.度數中心性ki越大,表示產業部門i在產業網絡中與產業部門的聯系就越多,在相應的投入產出表中作用就越重要,與其它產業部門進行的物質、副產品和能量的交互往來就越多.

2)密度

網絡的密度ρ反映網絡節點間聯系的緊密程度,表達式定義為

其中L為網絡中實際存在的有效關聯數,N為網絡中所有產業部門的個數.ρ越大,表示在相應的投入產出表中,產業部門間的聯系越緊密.

3)簇系數

在網絡中,網絡的簇系數是所有節點簇系數的均值,而節點的簇系數定義為

其中ei表示節點i的鄰居節點之間實際存在的邊的個數,ki表示節點i的度數中心性.

網絡的簇系數表示的內涵是,你的朋友圈或熟人圈中的每個人都是相互認識的.事實上,因為你的朋友大部分是你的同事、同學和鄰居,所以他們互相認識的概率自然應該很大.

4)平均最短距離

平均最短距離d是網絡的一個重要結構指標,網絡中所有節點之間的平均最短距離定義為

其中N為網絡中所有節點的個數,dij為連接節點i和j最短路徑上的邊的個數.

網絡中的搜索、路由等相關算法的高效實現皆與平均最短距離緊密相關.在相應的投入產出表中,平均最短距離越小,表示任意兩個產業部門之間的物質、副產品和能量的流動就越便捷.

2.3 演化情形

本文定義產業網絡中鏈路動態變化,為網絡中任意兩個節點之間物質流從一種狀態到隨后另一種狀態的變化情況.觀察歷年的產業網絡可以發現,節點之間的權重有衰減、保持不變和增加三種情形.由于節點對(u,v)之間的權重ω(u,v)往往隨著時間的變化而變化,因此可用ω(u,v,t),t∈[0,∞)表示網絡中節點對(u,v)之間的權重ω(u,v)是時間t的函數.在產業網絡中,任意一對節點之間的權重增減數值各不相同,為了便于定義隨后的預測得分,本文引進變化率r(0＜r＜1),基于任一t1時刻的產業網絡中任意一對節點(u,v)之間的權重ω(u,v,t1)(0),定義三個集合E1=[0,(1-r)ω(u,v,t1)),E2=[(1-r)ω(u,v,t1),(1+r)ω(u,v,t1)),E3=[((1+r)ω(u,v,t1),∞),顯然然后,視權重ω(u,v,t),t＞t1與三個集合的隸屬關系,把權重的演化情況分別分為衰減、保持不變和增加三種類型.

1)衰減

當產業網絡從t1時刻的狀態演化到t時刻的狀態時,若節點對(u,v)之間的權重ω(u,v,t)較權重ω(u,v,t1)為減少,且ω(u,v,t)∈E1時,定義此時的衰減函數為

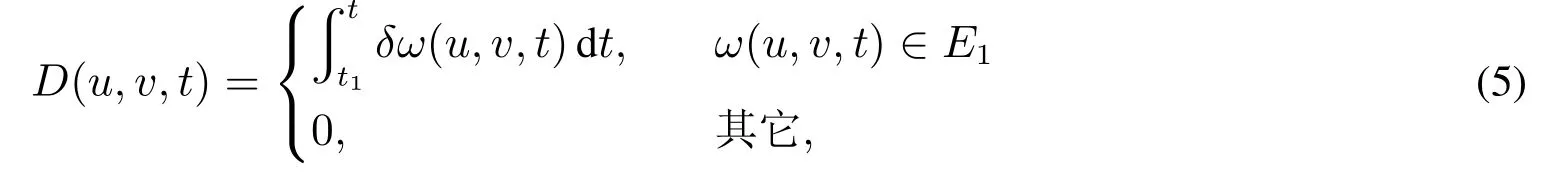
其中δ為負數,表示權重在衰減.

由于節點對之間的權重從t1時刻的狀態演化到t時刻的狀態時,其變化過程中權重是連續變化的,因此衰減函數可用積分表示.

2)保持不變

當產業網絡從t1時刻的狀態演化到t時刻的狀態時,若節點對(u,v)之間的權重ω(u,v,t)較權重ω(u,v,t1)變化不大,即ω(u,v,t)∈E2時,定義此時的不變函數為

其中η為非負數,表示權重的變化細微,可以忽略不計.

3)增加

當產業網絡從t1時刻的狀態演化到t時刻的狀態時,若節點對(u,v)之間的權重ω(u,v,t)較權重ω(u,v,t1)為增加,且ω(u,v,t)∈E3時,定義此時的增加函數為

其中θ為非負數,表示權重在增加.

由以上的定義可知,參數θ,δ和η的關系應為θ＞η＞δ,三者的數值將在評估預測算法的性能時確定,選擇預測精度最高的參數值.

2.4 基于鏈路動態變化的產業網絡預測得分

與相似性預測算法不同,本文提出的算法不僅考慮兩個節點之間的相似性程度受共同鄰居節點的影響,而且考慮前期網絡和當前網絡中,鏈路權重的變化程度,在考慮了變化程度的基礎上,又進一步考慮鏈路權重變化的方向,即權重的增減情況,來定義節點對(u,v)在區間[t1,t2],t2＞t1上的預測得分score(u,v)為

其中P(u,v,t)=D(u,v,t)IE1+C(u,v,t)IE2+I(u,v,t)IE3,S(u,v,t)=+P(y,v,t)],Γ(u)表示節點u的鄰居節點的集合,IEi,i=1,2,3是Ei的示性函數.

P(u,v,t)計算了產業網絡中節點對(u,v)從t1時刻的狀態演化到t時刻的狀態時的得分.假定節點y是節點u,v共同的鄰居節點,令S(u,v,t)表示分別與節點u,v相鄰的節點對(u,y)與(y,v),從t1時刻的狀態演化到t時刻的狀態時的所有得分之和.參數α是控制變量,表示鄰居節點影響到節點u和v之間關系的程度.score(u,v)就是基于鏈路動態變化的產業網絡預測模型的得分計算公式.特別,在ω(u,v,t1)=0的情形下,若ω(u,v,t)=0,則設P(u,v,t)=0；若ω(u,v,t)?=0,則設P(u,v,t)=θ.由此構建的式(8)包含了兩個節點間的相似性程度受共同鄰居節點的影響,節點間的鏈路權重變化程度,以及變化的方向等動態信息,其中利用三個連續區間E1、E2和E3,把投入產出表每五年更新一次,這種離散的跳躍,分別歸類到這三個區間,據此構建連續變化性模型,來預測當前產業網絡的鏈接情況.

2.5 模型的預測算法精度實驗設計及敏感性分析

2.4節提出的基于鏈路動態變化的產業網絡預測模型,既考慮了兩個節點之間的相似性程度受共同鄰居節點的影響,又考慮了在前期網絡和當前網絡中,鏈路權重的變化程度以及變化的方向.那么該模型的算法精度如何,本文將引入相關指標作進一步分析.目前,共有三種衡量鏈路預測算法精度的指標,分別為AUC(area under the receiver operation characteristic curve),Precision和Ranking score[35].它們對預測精度衡量的側重點不同.由于本文以整個產業網絡為研究對象,因此使用AUC指標從整體上來衡量算法的精度,并且產業網絡是小規模的網絡,因此本文在計算AUC時,采用逐項遍歷方法,即每次從網絡中選取一條邊進行測試,余下的邊作為訓練集,然后測試這條邊,得到一個相應的預測精度.最后遍歷網絡中的每條邊,計算平均值,作為整個網絡的預測精度.同時,在基于鏈路動態變化的產業網絡預測算法式(8)中,為了得到算法精度最優的參數值,本文將采用正交試驗設計[36],及其統計方法確定所需的參數,并分析數值模擬結果對相關參數的敏感性.

3 基于鏈路動態變化的產業網絡預測模型實證分析

本文以中國投入產出表為例,選出2005年、2007年、2010年和2012年的中國投入產出直接消耗系數表作為研究對象,以直接消耗系數為鏈路,產業部門為節點構建產業網絡.由于本文提出的預測算法,主要考慮產業網絡中鏈路動態變化的情況,即在產業網絡中保持節點個數不變,考察隨著時間的演化,網絡中任意兩個節點之間鏈路的斷開或鏈接情況,然后據此預測下一期的產業網絡.而在中國歷年的投入產出表中,產業部門的名稱和數目(網絡中的節點)并不是完全一致.因此,本文采用文獻[37]的處理方法,只對前后不統一的產業部門,即2005年的旅游業,2007年、2010年、2012年的水利、環境和公共設施管理業,對這兩個產業部門進行合并與整理,而其他的產業部門不會改動,因此在刪除這兩個產業部門后,對其余產業部門之間、產生的新鏈路或消失的鏈路影響甚微.鑒于此,把2005年投入產出表中旅游業所在的行與列刪除,把2007年、2010年、2012年投入產出表中的水利、環境和公共設施管理業所在的行與列刪除.利用前文構建產業網絡的方法,得到四個年份的有權重的、且是無向的產業網絡,如圖1所示,從左到右,從上到下分別是2005年、2007年、2010年和2012年的產業網絡.

圖1 四個年份的中國產業網絡Fig.1 China’s industrial network in four years

利用式(1)～式(4),對各個年份產業網絡的結構指標進行分析,得到的結果如表1所示.

表1 各個年份產業網絡的參數Table 1 Parameters of industrial network in each year

由表1可知,平均度和密度逐年減小,平均最短距離逐年增大,而簇系數沒有明顯的變化規律.結果表明物質、副產品和能量的循環流動可以到達更遠的產業部門,資源的利用更加充分,但從數值上看,這種變化又不太顯著.四個年份的產業網絡的平均度、密度、簇系數和平均最短距離的標準差很小,各項指標相似,說明四個產業網絡的結構非常接近,因此可以構建新的鏈路預測模型.

3.1 產業網絡的預測

由于我國投入產出表每五年編制一次,中間年份再出一次延長表,分別于1997年、2002年、2007年和2012年四個年份出版,而2000年、2005年和2010年的表格是投入產出表的延長表.其中2005年以前的投入產出表距本文所預測的2015年投入產出關系已達十多年之久,對于預測結果無顯著的影響.因此,本文將用2005年、2007年、2010年和2012年的產業網絡,去預測下一年份即2015年產業網絡的鏈接情況.這四個年份的結構指標在上節已做了詳細分析,結果非常接近.因此,可以利用基于鏈路動態變化的產業網絡預測模型中的式(8),計算2015年產業網絡中任意兩個節點之間的得分,再利用2.1節中產業網絡模型的構建方法,得到2015年的產業網絡.進而,可將2015年產業網絡的預測結果、與過去幾年的真實數據相比較,分析產業的轉型升級、遷移等情況.下面將以產業網絡結構指標中的度數中心性為例,分析產業重要性的演化情況.利用式(1),計算預測得到的2015產業網絡中各個產業的度數中心性,再與2005年和2010年相比較,結果如表2所示.

從表2可以看出,批發和零售業度數中心性在2005年的網絡中居于第九位,2010年網絡中上升到第二位,最后來到了2015年網絡中的第一位,重要性可見一斑.事實上,批發和零售業是各個產業部門的產品實現價值的重要媒介,是連接商品生產和消費的主要環節.除了批發和零售業以外,化學工業度數中心性的位置也在提升,由2005年的第七位,到2010年的第四位,最后上升到2015年的第二位,可見其在當下產業網絡中的重要性.度數中心性發生顯著變化的還有金融業,由2005年和2010年的前十位以外進入到2015年的第四位,它在產業網絡內度數中心性位置的提升,說明了其是配置社會資源和融通資金作用的源動力,是現在經濟生活的命脈和媒介.批發和零售業與金融業屬于第三產業,“十二五”規劃結束后,第三產業的度數中心性在前十個產業中占到了六席,產業結構優化調整的效應從預測得到的產業網絡中得到了充分的體現.為了得到預測方法精度,下節將給出計算預測算法精度的實驗設計和敏感性分析.

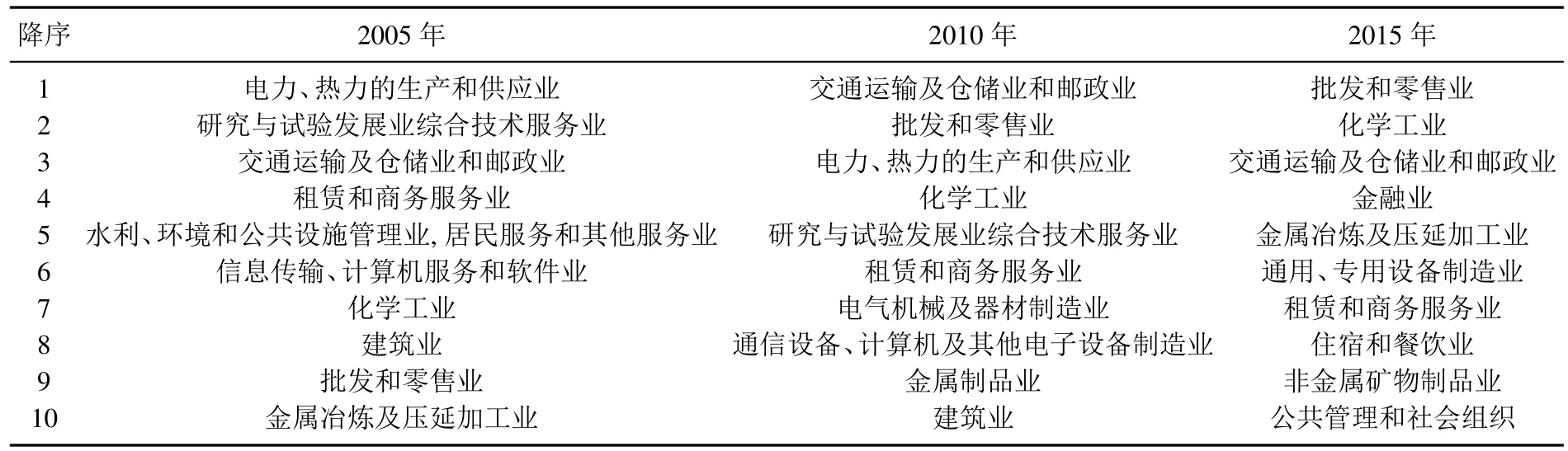
表2 三個年份度數中心性排在前十的產業部門Table 2 Three-year-degree centrality ranked in the top ten of the industry sector

3.2 產業網絡預測算法精度實驗設計及敏感性分析

實例數據來源于上節所構建的2005年、2007年、2010年和2012年的產業網絡,依據預測精度指標AUC,通過正交試驗設計和對參數的敏感性分析,給出基于鏈路動態變化的產業網絡預測模型參數的最優設定值.

1)正交試驗設計

在基于鏈路動態變化的產業網絡預測算法式(8)中,為了得到算法精度最優的參數值,本文將采用正交試驗設計及其統計方法確定所需的參數,并分析參數的敏感性.正交試驗設計(orthogonal experimental design)是多因素多水平的實驗設計方法[36],依據具體問題選擇合適的正交表是使用正交法的關鍵.在基于鏈路動態變化的產業網絡預測算法中,共有五個參數,依據各個參數所表示的不同意義,r、α和θ分別選取兩個水平,δ選取四個水平,η選取五個水平,在此基礎上設計正交表.然后,依據正交表進行仿真實驗,并將結果列表示意.α的兩個水平分別設為0.05和0.1,先分析α=0.05的情況,再分析α=0.1的情況.當α=0.05時,利用網絡的兩個版本進行研究.一個是基于四個權重產業網絡,當變化率r設為25%,另一個變化率r設為50%.計算不同版本下的AUC值并列表顯示.當變化率r設為25%,且α=0.05,θ=2時,通過MATLAB 7.0編程計算得到AUC值,如表3所示.當變化率r設為25%,且α=0.05,θ=3時,AUC的值,如表4所示.

表3 變化率r設為25%時AUC的值(α=0.05,θ=2)Table 3 The AUC values underr=25%(α=0.05,θ=2)

表4 變化率r設為25%時AUC的值(α=0.05,θ=3)Table 4 The AUC values underr=25%(α=0.05,θ=3)

當變化率r設為50%,且α=0.05,θ=2時,AUC的值,如表5所示；當變化率r設為50%,且α=0.05,θ=3時,AUC的值,如表6所示.

從表3～表6可以看出,預測精度AUC最大是表5中的值0.979 3,相應的參數δ,η,θ取值分別為-0.5,0.5,2,同時r=0.5.當α=0.1時,仍然利用產業網絡的兩個版本進行研究.一個是基于四個權重產業網絡,當參數α變化率r設為25%,另一個變化率r設為50%,計算不同版本下的AUC值.計算的方法同α=0.05時的情況,這里就不再贅述.比較分析得到的結果發現,當α,r,δ,η和θ的取值分別為0.05、0.5、-0.5、0.5和2時,預測精度AUC最大.

表5 變化率r設為50%時AUC的值(α=0.05,θ=2)Table 5 The AUC values underr=50%(α=0.05,θ=2)

表6 變化率r設為50%時AUC的值(α=0.05,θ=3)Table 6 The AUC values underr=50%(α=0.05,θ=3)

2)參數的敏感性分析

由以上分析的結果可知,當分別以r=0.5和r=0.25,α=0.05和α=0.1,對預測精度AUC進行變化分析時,得到鏈路預測算法中各個參數α,r,δ,η和θ的取值分別為0.05、0.5、-0.5、0.5和2時,預測精度AUC最大.為了研究數值模擬結果對這兩個參數的敏感性,在此做一個敏感性分析,以一定區間的取值范圍為參考,考慮r和α對預測精度AUC的變動趨勢.不失一般性,r的取值范圍為[0.1,0.8],間距設為0.05；α的取值范圍為[0,1.5],間距設為0.05,計算其對預測精度AUC的影響,得到趨勢圖2.當r在[0.1,0.8]范圍內取值時,得到預測精度AUC的極差為0.058 3,均值為0.960 3和標準差為0.018 6；而當α在[0,1.5]范圍內取值時,得到預測精度AUC的極差為0.161 3,均值為0.867 3和標準差為0.052 8.可見,預測精度對這些參數的變化不很敏感,但α比r的敏感性要高,說明在計算預測精度時,優先考慮到兩個節點的關系受到鄰居節點的影響程度.

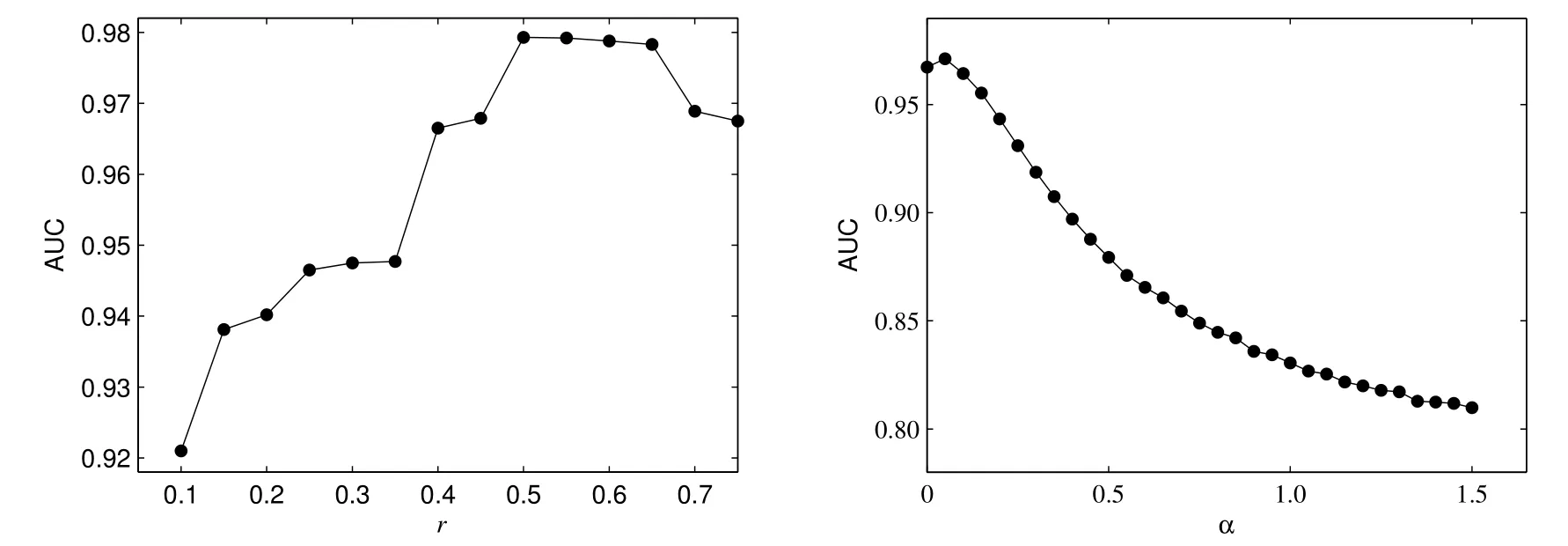
圖2 AUC的變化趨勢Fig.2 The change trend of AUC values

3.3 預測算法精度的對比分析

為了測試本文提出的預測算法性能的優劣,進一步引入相似性鏈路預測算法作為對比.相似性鏈路預測算法指標有兩類,一類是基于無權網絡的相似性指標,如式(9)～式(12)所示；另一類是基于權重網絡的指標,如式(13)～式(16)所示.它們分別為CN指標(common neighbors,又稱結構等價指標)、RA指標(resource allocation指標,資源分配指標)、JC指標(Jaccard’s coefficident指標,約旦系數指標)和AA指標(Adamic-Adar指標,阿達米克－亞達指標)[32-34].這八個指標的具體表示式為

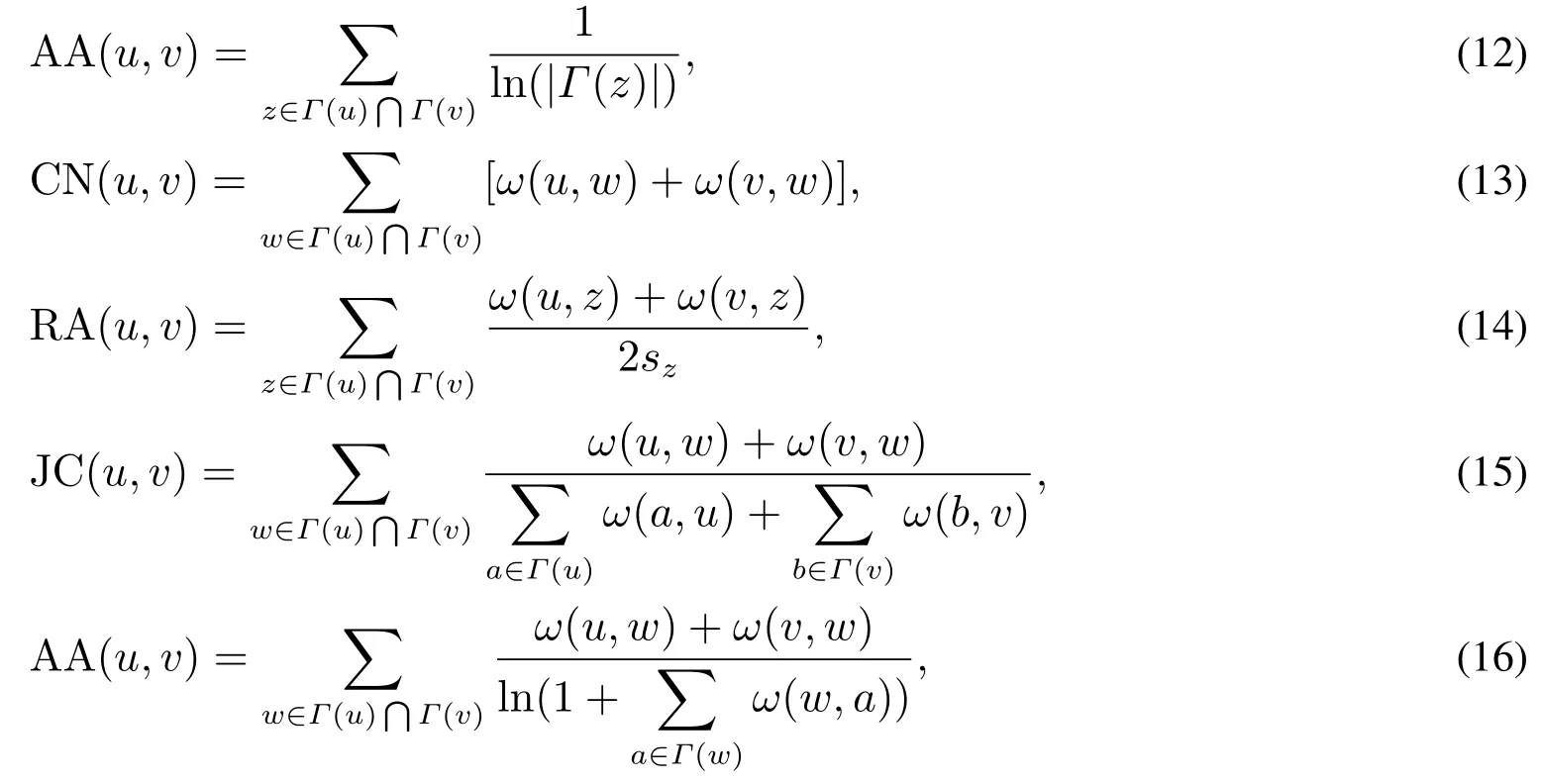
其中Γ(u)和Γ(v)分別表示節點u和v的鄰居節點的集合,|Γ(z)|表示節點z的度,sz表示節點z的強度.

在文獻[32—34]中,沒有考慮節點u,v之間的權重ω(u,v)與時間的關系,因此式(13)～式(16)中只利用ω(u,v)表示節點u,v之間的權重,而本文提出的預測模型中考慮了節點u,v之間的權重ω(u,v,t)與時間相關,并據此提出了基于鏈路動態變化的產業網絡預測模型.許小可等[38]研究發現,如果任意兩節點之間的最短距離長度大于等于2時,那么可以使用以上基于共同鄰居算法的八種鏈路預測算法.由于在2005年、2007年、2010年和2012年的產業網絡中,任意兩節點之間的最短距離長度大于等于2,因此,可以使用相似性鏈路預測算法作比較.

截至目前,由于2015年包含42部門的投入產出表,尚未對外公布,因此無法分析2015年產業網絡的真實情況.因此本文采用鏈路預測中的常用做法,再結合本文研究的產業網絡的特征,利用2.5節中所介紹的預測精度指標AUC,去衡量本文算法與相似性鏈路預測算法哪個更加優越.現將相似性鏈路預測算法的精度AUC,計算得到的結果,列于表7.

表7 相似性鏈路預測算法的精度AUCTable 7 The AUC values of prediction accuracy based on similarity link prediction algorithm

其中AUC的最大值為0.840 8,而基于鏈路動態變化的產業網絡鏈路預測算法的精度為0.979 3.與相似性鏈路預測算法的精度相比較,顯然本文算法的預測精度最大.因此在預測產業網絡的鏈路時,不僅要考慮產業網絡當前的鏈接情況,還要充分考慮產業網絡的演化情況,這樣得出的結果才會更加準確可靠.

4 結束語

當考慮了產業網絡的鏈路動態變化因素時,通過對中國2005年、2007年、2010年和2012年產業網絡的拓撲結構及鏈路權重變化的分析,提出了一種新的產業網絡預測算法模型.新的預測算法不僅考慮了產業網絡中鏈路的動態變化信息,而且考慮到兩個節點鄰居的得分情況,在權重的特定比例上定義預測得分的增加或減少,最后把每個變化過程的得分相加即得產業網絡的鏈路預測得分.實證結果表明,利用正交實驗設計方法,只要其中的參數選取合適,則新的產業網絡預測算法模型具有理想的預測精度.并且相比于相似性鏈路預測算法,本文提出的基于鏈路動態變化的產業網絡預測模型的預測精度更加理想.因此鏈路上的動態變化信息對預測產業網絡具有重要意義.

為使產業網絡的預測更加準確,研究者們應該充分考慮過往信息對產業網絡鏈路預測的重要性.由于數據的易得性,本文僅僅考慮了中國產業網絡的演化情況.其實,產業網絡(產業共生網絡)形態各異,既有宏觀上的產業網絡,又有中觀或微觀上的產業網絡,深入研究這些網絡的鏈路預測很有意義,可以指導產業的升級或遷移等問題.在將來的工作中,將更加注重這方面的研究.