Boost變換器的環路補償設計

(廣西大學 電氣工程學院，廣西 南寧 530004)

1 引言

一直以來，開關電源中環路的補償和計算都是一個難點問題，也是工程應用中需要重點關注的部分。在開關電源的設計中需要使電源擁有一個良好的靜態指標和動態指標，這就要求在人們除了對主電路進行精心計算還需要一個良好的反饋控制系統，而補償網絡直接影響著反饋回路的性能因此補償回路的設計非常重要。由于在開關變換器中電感的等效串聯電阻和輸出濾波電容的等效串聯電阻ESR會給變換器引入一個右半平面的零點，從而對整個環路的設計帶來影響，因此分析這兩個電阻對環路所帶來的影響有著重要的研究意義[1-2]。

本次設計是以傳統的Boost變換器為例，來研究非線性器件中的等效串聯電阻對變換器環路所帶來的影響，并應用小信號分析法建立模型，最后利用仿真分析來驗算系統的合理性[3]。

在開環增益為1時，系統的總開環相位延遲必須小于360°。在截止頻率出開環相位延遲小于360°的角度稱為相位裕量。為使系統在最惡劣情況下仍能穩定，要求系統至少有35°到45°的相位裕量。據此原則進行環路設計，可以實現在溫度發生變化或負載突變時都能滿足穩定調節[4-5]。

2 本次設計的主要技術指標

輸入電壓：Vin=10V；輸出電壓Vo=20V；開關頻率f=50kHz；電感L=20uH，RL=0.005Ω；電容C=1000uF，RC=0.005Ω，R1=10kΩ，R2=10kΩ。

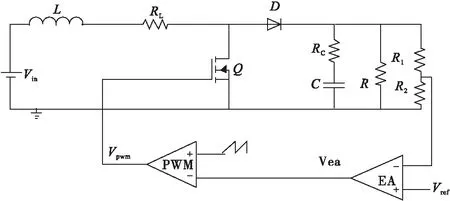
圖1 Boost變換器的原理圖

其負反饋控制框圖如圖2所示。

圖2 Boost變換器的閉環控制系統

其中Gvd(s)為變換器的占空比d(s)到輸出電壓Vo(s)的傳遞函數，Gm(s)為PWM脈寬調制器的傳遞函數，H(s)表示反饋網絡的傳遞函數，G(s)為補償網絡的傳遞函數[6]。

(1)

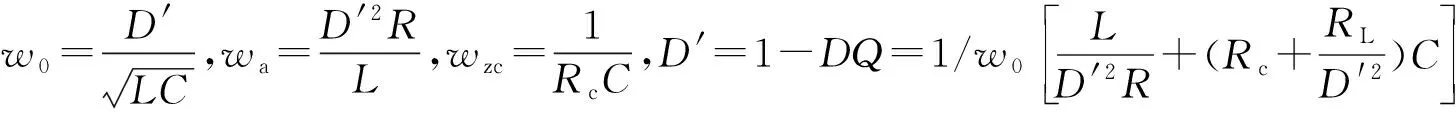
PWM脈寬調制信號的傳遞函數為：

Gm(s)=1/Vm

(2)

反饋網絡的傳遞函數為：

H(s)=R2/(R1+R2)

(3)

因此Boost變換器的回路增益傳遞函數為：

(4)

由式(4)可以看出Boost變換器的傳遞函數存在一個右半平面的零點，為了避免此零點引起過多的相移，一般取環路帶寬為其頻率的1/4～1/5，此處取1/5即fg=10kHz[7]。

3 Boost變換器補償網絡的設計

將Boost變換器的參數數據代入式(4)中得到：

(5)

用Matlab來分析不加補償器時Boost變換器的Bode圖，如圖3所示。

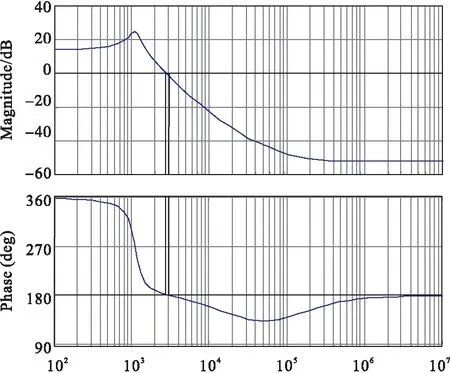
圖3 不加補償網絡的Bode圖

從上圖中可以看出在低頻時增益保持不變，整個增益以-40dB/decade穿越0dB線，穿越頻率fc=2.76kHz。相位裕度為2.07°，顯然系統是一種不穩定的狀態，需要添加補償網絡來提高系統的穩定性，所添加的補償網絡在fg處應該提供一個+20dB/decade的斜率，采用雙零雙極點補償電路，如圖4所示[8]。

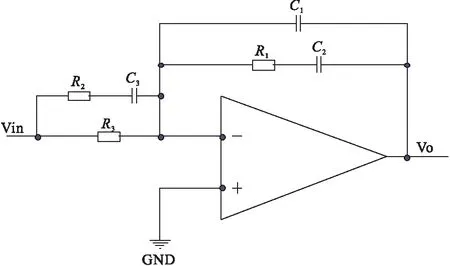
圖4 補償電路

傳遞函數：

(6)

補償網絡為有源超前-滯后網絡，有兩個零點、三個極點(R3≥R2，C2≥C1)。零點頻率為:

(7)

極點頻率為：

(8)

設置控制器的兩個零點均為fz1=fz2=0.5fp0=563Hz；第一個極點fp1用來抵消右半平面的零點fz，fp1=fz=19.9kHz；第二個極點fp2用來增加高頻衰減率，其值為fp2=10fc=27.6kHz。設R1=10kΩ，在高頻段的電壓放大倍數為Av2=(fp1/fc)*42=R1/R2=300，可得R2=33Ω，將上述參數代入到式(7)、(8)中得出相應為參數為：

C2=28.3nF，C3=0.242μF，C1=577pF，R3=1.2kΩ

補償函數為：

(9)

補償后的系統Bode圖如圖5所示。

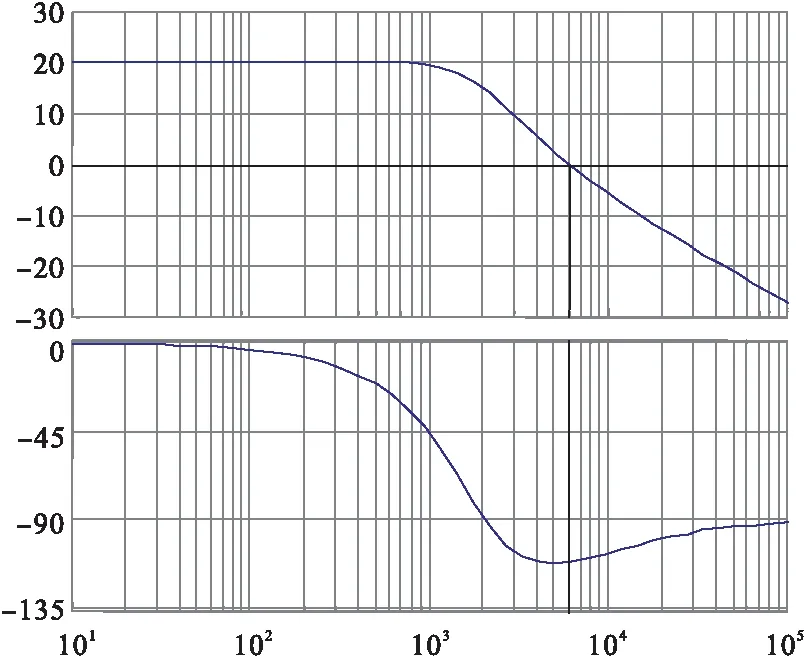
圖5 補償后的Bode圖

從圖中可以看出系統的相位裕度為68.4dB，穿越頻率為6.09kHz。此時整個系統是處于穩定的狀態。

4 結論

本文利用Boost變換器的小信號傳遞函數，將控制理論與變換器的環路補償相結合，通過設計合適的相位裕量來保證開關電源的穩定性，其過程經實驗證明具有較好的通用性，對實際電路中參數的選取具有很好的指導意義。