壓電噴油器壓電執行器熱-電-機械耦合遲滯特性

孟育博,張幽彤,王志明,張曉晨,樊利康,李 濤

(1.山東大學 能源與動力學院,濟南250011;2.北京理工大學 機械與車輛學院,北京100081)

0 引 言

壓電陶瓷元件由于壓電效應和逆壓電效應而作為傳感器或執行器被廣泛應用于工業中。同時這些驅動由于響應快、輸出力大和緊湊設計等特性被用于現代發動機噴油系統中,基于壓電堆的噴油器被用于燃油噴射閥的開啟與閉合[1,2]。由于壓電執行器相比于傳統的電磁閥執行器具有更快的響應速度,因此能夠對多次噴射之間的時間間隔進行精確控制,有助于降低排放。同時,基于壓電堆的噴油器能夠提高噴油壓力,可以達到250 MPa;噴油壓力越高,噴油量越精確,燃燒越高效。當壓電堆用作執行器應用時,采用式(1)進行線性壓電材料的描述[3]。

式中:S3為應變;T3為機械應力;E3為電場強度;為順應彈性系數;為固定應力下的壓電系數。此外,加工企業的數據庫也僅有這些方程和參數。

由于執行器工作在較寬的工作范圍中,且大部分時間工作在非線性狀態,線性工作方式只占較小的一部分,因此式(1)不能全面描述執行器的特性[4,5]。對于壓電材料而言,非線性遲滯現象是其基本特征且對壓電執行器的精確控制具有很大的影響,因此遲滯特性不可忽略。相應的,由于噴油器處在發動機缸蓋十分關鍵的位置,因此溫度的影響也不可忽略。

壓電致動器在正常運行情況下的性能和可靠性是促進壓電執噴油器技術進一步發展的關鍵。因此,壓電執行器的研究得到廣泛的關注。應力、溫度對壓電執行器性能的影響已有相關的研究[6,7]。在文獻[8]中應力和電場的綜合效應已經被分析,文獻[9]中溫度和電場的綜合效應也被研究,并得出在固定預緊力條件下壓電耦合系數的多項式:

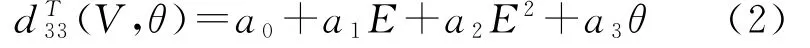
式中:E為電場強度;θ為溫度;a0、a1、a2、a3為試驗耦合系數。

文獻[10]對執行器位移的增加進行試驗分析,而文獻[11]對位移的增加嘗試從物理的角度進行解釋。在壓電執行器的實際應用中,輸入場(例如電場、機械場和溫度場)都不是恒定的。因此,在耦合遲滯建模過程中,需要對材料甚至整個執行器有一個精確的描述。

為了提高壓電執行器的控制精度,國內外學者對壓電陶瓷執行器數學模型進行研究。提出了模擬其遲滯特性的Preisash模型、Maxwell模型、Dahl模型和Duhem模型等。

Preisash模型是最常用的數學模型之一[12],但是存在在線實現復雜的缺點;Maxwell模型存在求解計算過程過于復雜的缺點[13];Dahl模型參數較多,參數的辨識過程比較復雜[14]。而Duhem模型是輸入信號導數的函數,模型輸出與輸入信號的速率相關,符合壓電材料中遲滯非線性的動態特性,能夠更精確地描述壓電致動器的遲滯特性[15]。

本文研究了應用于噴油器的壓電執行器的遲滯特性。在準靜態條件下對壓電致動器熱-電-機械性能進行測試。在試驗的基礎上,對所建立的模型參數進行辨識并進行試驗驗證。

1 試驗設置

一般而言,壓電執行器產生的最大應變為0.1%～0.15%[16],且壓電堆執行器由許多層壓電執行器片組成,如圖1所示,因此壓電堆執行器的位移是單層壓電執行器片位移的總和。在本文中,商業應用的鋯鈦酸鉛壓電堆執行器被用于試驗研究。執行器使用溫度范圍為－20～120℃,居里溫度為240℃。表1顯示了用于試驗研究的執行器的幾何結構和產品性能。

圖1 壓電執行器結構示意圖Fig.1 Structure of piezoelectric actuator

壓電堆執行器的測試裝置原理圖如圖2所示,壓電堆執行器固定在預緊力測試裝置中,采用矩形彈簧(47 N/mm)和螺母進行預緊力的施加,通過旋轉螺母改變彈簧的形變來改變預緊力的大小,同時采用力傳感器(量程為0～3 k N,精度為滿量程的0.3%)進行預緊力的測試。預緊力裝置固定在夾具上;加熱裝置安裝在預緊力裝置外,熱電偶(量程為－20～200℃,偏差為±1.5℃)用于溫度的測量,溫度調節通過PID控制器來完成。采用激光位移傳感器(量程±1 mm,分辨率0.1μm)測量位移,并把信號傳輸到處理設備,用于執行器輸出特性的研究。

表1 PZT執行器特性Table1 Characteristics of PZT actuator

圖2 測試裝置示意圖Fig.2 Diagram of test equipment

2 固定機械載荷下的測試

為了研究機械載荷對壓電執行器特性的影響,按照下述測試方法進行測試:①預緊機械載荷從小(例如200 N)到大逐漸增加;②電壓采用單極驅動,最大電壓為150 V;③測試溫度為25℃。

圖3為不同機械載荷下的電壓-位移曲線,電壓信號頻率為5 Hz。由圖可以看出,預緊機械載荷不僅影響壓電堆執行器峰值大小,并且還影響遲滯曲線的形狀和面積。由于預緊力能夠影響執行器自生熱,因此在設計預緊機械載荷時應當考慮對遲滯曲線形狀的影響。壓電堆執行器遲滯環所代表的能量正是執行器生熱的主要來源。

圖3 不同載荷下的遲滯曲線Fig.3 Hysteresis curve under different load

圖4中,峰值位移作為預緊力的函數被記錄,預緊力為[200,1200]N。最大位移出現在大約800 N。相對于200 N時的位移輸出,800 N時的位移輸出增加約4.3μm。應當注意的是,在所給執行器數據中這個值為29μm,也就是預緊力為0 N的值。因此,這個預緊力數值可以作為壓電執行器基礎結構優化設計的參考值。

圖4 不同載荷下的峰值位移Fig.4 Peak displacement under different load

3 固定溫度的測試

為了評估溫度對壓電執行器特性的影響,根據下面的設置進行一系列的評估測試:①采用測試2中所加的預緊力;②電壓采用單極驅動,最大電壓為150 V;③溫度變化從25℃到80℃。

圖5是在載荷(預緊力)為800 N、頻率為5 Hz、電壓從0到150 V時,不同溫度下的電壓-位移曲線。溫度對壓電堆執行器的影響主要體現在,在一定的范圍內壓電堆執行器隨著溫度的升高總體呈現上升的趨勢。為了定量研究溫度對位移輸出的影響,特別把在電壓為150 V時不同溫度下的位移值提取出來,如圖6所示。

圖5 預緊力為800 N時的遲滯曲線Fig.5 Hysteresis curve when load is 800 N

圖6 預緊力為800 N時位移隨溫度的變化曲線Fig.6 Displacement curve changes with temperature when load is 800 N

由圖6可以看出,在溫度從25℃到增加到60℃時,位移增加約為0.6μm,從60℃到增加到80℃時,位移增加約為0.1μm。因此,壓電執行器在從25℃到60℃時,溫度對位移輸出的影響較大;從60℃變化到80℃過程中,影響逐漸減小。而應當注意的是,廠家所提供的是常溫下預緊力為零時獲得的位移。

4 遲滯模型搭建和仿真

4.1 遲滯模型

Duhem模型是一種動態模型,該模型最大的優點就是具有明確的數學表達式,適當地調整模型參數可以準確反映不同遲滯非線性,因此選用Duhem遲滯模型對壓電陶瓷系統非線性建模。Duhem模型的基本表達式為:

式中:Ve為施加到壓電堆(無壓電效益)電容的電壓;S為輸出位移;α為權重系數且α＞0;f(Ve)和g(Ve)為表達非線性的兩個輔助函數。

根據Weierstrass第一逼近定理,對Duhem模型中的連續函數f(Ve)和g(Ve),在滿足精度σ＞0條件下,應用多項式函數進行逼近。設f(Ve)、g(Ve)階次分別為n、m,令,其多項式分別為:

為了便于對參數進行辨識,取m＝5,n＝5。

由文獻[17]可知,壓電執行器電壓降可以表示為:

式中:Ve為輸出電壓;Vp為壓電執行器上的電壓降;Q為機電耦合系數;Cp為電容。

由機電耦合系數與壓電材料的關系可得機電耦合系數的表達式為:

式中:A為壓電堆有效面積;h為單層厚度;d(T)為電壓系數。

同理可計算出壓電堆整體的電容:

式中:N為壓電執行器層數;εT為介電系數。

根據文獻[18]可得電壓系數和溫度之間的關系式:

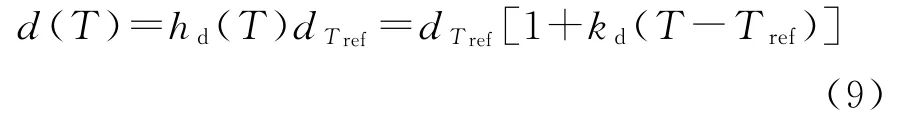
式中:Tref＝20℃;d Tref為相對溫度下的壓電系數;hd(T)為相對溫度的乘數因數;kd為擬合因數,且應修改為ηd。

4.2 仿真結果分析

根據試驗結果,采用Matlab對方程(2)的參數α、f(Ve)和g(Ve)進行辨識,通過對參數的調整,使試驗結果和模擬結果實現良好的一致性。

在25℃,機械載荷為800 N時壓電執行器仿真和試驗結果如圖7所示,誤差如圖8所示。

由圖7和圖8可以看出,模型的輸出和試驗數據基本吻合,相對誤差小于5%,主要出現在最大輸入電壓的中間,原因可能是由于遲滯方程的簡化。

圖7 模型擬合結果Fig.7 Experimental result and model result

圖8 模型擬合的相對誤差Fig.8 Relative error between measured displacement and simulation

為了得到不同溫度下的仿真結果,根據所測試的不同溫度下的試驗結果,對參數ηd進行辨識。辨識結果如圖9所示。ηd通過對試驗結果的擬合得到,擬合值為:Kd＝1.5×10－3℃－1。

圖9 乘數因子與溫度之間的線性關系Fig.9 Linear relationship between multiplier factor and temperature

在相同的驅動電壓下,三個不同溫度條件下的試驗和仿真結果如圖10所示。由圖10可以看出,不同溫度下試驗數據和仿真結果具有良好的一致性。為相似壓電執行器的遲滯現象的控制和控制精度的提高奠定良好的基礎。

圖10 不同溫度下的試驗和仿真結果Fig.10 Experimental and model results at different temperatures

5 結 論

(1)本文對應用于噴油器中的壓電執行器準靜態遲滯特性進行測量,得到在不同預緊力、不同溫度條件下的位移遲滯曲線。在預緊力為200～1200 N范圍內,壓電執行器輸出特性隨著預緊力的增大呈現先增大后減小的趨勢。壓電執行器位移輸出特性在800 N時達到最大值,比200 N時的位移增加約4.3μm;在溫度為25～80℃范圍內,預緊力為定值時,壓電執行器位移輸出特性隨著溫度的增加而增加。在溫度從25℃增加到60℃時,位移增加約為1.8μm,從60℃增加到80℃時,位移增加約為0.2μm。

(2)一個包括壓電堆遲滯特性和溫度影響的數學模型被用來對試驗結果進行模擬。在不同溫度下試驗數據和仿真結果具有較好的一致性。模型為執行器遲滯特性的控制提供了良好的基礎。

[1]Biggio M,Butcher M,Giustiniani A,et al.Memory characteristics of hysteresis and creep in multi-layer piezoelectric actuators:an experimental analysis[J].Physica B,2014,435(1):40-43.

[2]衛海橋,裴自剛,馮登全,等.壓電噴油器多次噴射對GDI汽油機顆粒物排放的影響[J].吉林大學學報:工學版,2016,42(1):1-8.Wei Hai-qiao,Pei Zi-gang,Feng Deng-quan,et al.Effect of multi-injection with piezo injection on particulate emission in gasoline direct injection engine[J].Journal of Jilin University(Engineering and Technology Edition),2016,42(1):1-8.

[3]高長銀.壓電效應新技術及其應用[M].北京:電子工業出版社,2011.

[4]Webber K G,Franzbach D J,Koruza J,et al.Determination of the true operational range of a piezoelectric actuator[J].Am Ceram Soc,2014,97(9):2842-2849.

[5]Jiang W,Zhang R,Jiang B,et al.Characterization of piezoelectric materials with large piezoelectric and electromechanical coupling coefficients[J].Ultrasonics,2003,41(2):55-63.

[6]Senousy M S,Li F X,Mumford D,et al.Thermo-electro-mechanical performance of piezoelectric stack actuators for fuel injector applications[J].Journal of Intelligent Material Systems and Structures,2009,20(4):387-399.

[7]Han Y M,Moo B K,Choi S B.Control performance investigation of piezoelectric actuators under variation of external heat environment[J].Trans Korean Soc Noise Vib Eng,2015,25(10):707-713.

[8]Butcher M,Davino D,Masi A,et al.An experimental evaluation of the fully coupled hysteretic electromechanical behavior of piezoelectric actuators[J].Physica B,2016,486:116-120.

[9]Senousy M,Rajapakse R,Gadala M.Experimental investigation and theoretical modeling of piezoelectric actuators used in fuel injectors[J].IUTAM Bookseries,2011,24:219-227.

[10]Koruza J,Franzbach D J,Schader F,et al.Enhancing the operational range of piezoelectric actuators by uniaxial compressive preloading[J].Applied Physics,2015,48(21):215-302.

[11]Dittmer R,Webber K G,Aulbach E,et al.Optimal working regime of lead-zirconate-titanate for actuation applications[J].Sensors and Actuators A Physical,2013,189(2):187-194.

[12]Lin S I E.The theoretical and experimental studies of a circular multi-layered annular piezoelectric actuator[J].Sensors and Actuators A Physical,2011,165(2):280-287.

[13]Quant M,Elizalde H,Flores A,et al.A comprehensive model for piezo ceramic actuators:modelling,validation and application[J].Smart Materials and Structures,2009,18(12):125011.

[14]Xu Q S,Li Y M.Dahl model-based hysteresis compensation and precise positioning control of anXYparallel micromanipulator with piezoelectric actuation[J].Journal of Dynamic Systems,Measurement and Control,2010,132(4):041011.

[15]Ossart F,Meunier G.Comparison between various hysteresis models and experimental data[J].Journal of Applied Physics,1990,67(9):5379-5381.

[16]Grunbichler H,Kreith J,Bermejo R,et al.Influence of the load dependent material properties on the performance of multilayer piezoelectric actuators[J].Springer Netherlands,2011,24:243-253.

[17]Fukada E.History and recent progress in piezoelectric polymers[J].IEEE Transactions on Ultrasonics,Ferroelectrics and Frequent Control,2000,47(6):1277-1290.

[18]Leonardo A,Andrea T.Piezoelectric injectors for automotive applications:modeling and experimental validation of hysteretic behavior and temperature effects[J].Journal of Dynamic Systems,Measurement and Control,2013,135(1):011005.