基于滑動(dòng)平均法的軌道交通短時(shí)客流實(shí)時(shí)預(yù)測(cè)

孟品超,李學(xué)源,賈洪飛,李延忠

(1.長(zhǎng)春理工大學(xué) 理學(xué)院,長(zhǎng)春130022;2.吉林大學(xué) 交通學(xué)院,長(zhǎng)春130022;3.北華大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,吉林省吉林市132013)

0 引 言

軌道交通中滑動(dòng)平均法模型簡(jiǎn)單易用,目前多用于對(duì)數(shù)據(jù)預(yù)處理,如裴益軒等[1]在實(shí)例應(yīng)用中用滑動(dòng)平均法給出了濾掉高頻干擾信號(hào)的算法;胡松等[2]用滑動(dòng)平均法濾波衰減了較高頻率的噪聲信號(hào),達(dá)到提高信噪比的目的;何耀等[3]在所提出模型的基礎(chǔ)上,采用滑動(dòng)平均濾波法削弱噪聲項(xiàng)干擾,起到了較好的估計(jì)效果。Hatchett等[4]鑒于較長(zhǎng)移動(dòng)平均效果差的狀況,重新給出了移動(dòng)平均最佳長(zhǎng)度的建議。Shih等[5]將N點(diǎn)滑動(dòng)平均的方法應(yīng)用到普通示波血壓確定過(guò)程,從而在可接受精確度范圍內(nèi)非常方便且無(wú)創(chuàng)地獲得中樞主動(dòng)脈收縮壓值。

軌道交通客流具有周期性,每天客流波動(dòng)具有一定規(guī)律性。客流時(shí)間序列在每天同一時(shí)間段客流量具有相似性,其構(gòu)成的時(shí)間序列具有一定的平穩(wěn)性。因此,可采用滑動(dòng)平均法對(duì)歷史客流數(shù)據(jù)在每天同一時(shí)間間隔內(nèi)構(gòu)成的時(shí)間序列進(jìn)行建模,并采用滑動(dòng)平均法[6]來(lái)一步預(yù)測(cè)相同時(shí)間間隔內(nèi)的客流量。滑動(dòng)平均模型簡(jiǎn)單,不需大量樣本,且計(jì)算速度快,具有較高的預(yù)測(cè)精度。故本文提出了一種基于滑動(dòng)平均法的軌道交通短時(shí)客流預(yù)測(cè)算法。

1 滑動(dòng)平均法

1.1 基本算法

總體上波動(dòng)較為平穩(wěn)的離散時(shí)間序列{y t}可看成規(guī)律性成分的穩(wěn)定性部分{f t}和受噪聲因素影響的隨機(jī)性波動(dòng){e t}兩部分組成,故較為平穩(wěn)的離散時(shí)間序列{y t}可分成兩部分:

為減弱隨機(jī)誤差{e t}影響,通常可對(duì)總樣本量為N的原始時(shí)間序列數(shù)據(jù){y t}作滑動(dòng)平均處理,即對(duì)非平穩(wěn)的時(shí)間序列{y t},在合適的樣本量為n的小區(qū)間上看作近似平穩(wěn)的,其中n為滑動(dòng)平均參數(shù),然后在這個(gè)近似平穩(wěn)的區(qū)間上采用式(2)進(jìn)行平均處理,得到的值可以作為下一時(shí)刻的預(yù)測(cè)值。

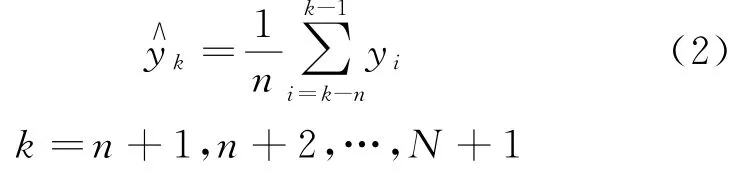
對(duì)于時(shí)間序列{y t}逐一對(duì)各小區(qū)間內(nèi)數(shù)據(jù)進(jìn)行局部平均化處理,得到減弱了噪聲因素{e t}影響的預(yù)測(cè)時(shí)間序列。這樣滑動(dòng)平均所得到的},隨機(jī)波動(dòng)因受到平均的作用而比原時(shí)間序列{y t}減小了,也就是更加平滑了。

1.2 平均相對(duì)誤差檢驗(yàn)

針對(duì)預(yù)測(cè)算法的精度,Dhuyvetter and Kastens[7]采用平均絕對(duì)誤差的方法衡量預(yù)測(cè)精度,Hatchett[8]考慮使用均方根誤差來(lái)衡量預(yù)測(cè)精度,這兩種衡量方法效果差別不大。本文擬采用消除量綱影響的平均相對(duì)誤差來(lái)比較不同滑動(dòng)參數(shù)下的預(yù)測(cè)誤差。

取不同的滑動(dòng)參數(shù)n就會(huì)有不同的滑動(dòng)平均結(jié)果[9],滑動(dòng)參數(shù)n過(guò)小,起不到抑制隨機(jī)波動(dòng)的作用;滑動(dòng)平均參數(shù)n過(guò)大,越顯均勻,但同時(shí)可能濾掉高頻變化的規(guī)律性部分,導(dǎo)致總體預(yù)測(cè)精度不好。因此,應(yīng)該選擇一個(gè)較為合理的滑動(dòng)參數(shù)n值來(lái)做滑動(dòng)平均。選擇較合理的滑動(dòng)參數(shù)n的方法是,選取不同的滑動(dòng)參數(shù)n值,計(jì)算不同n值對(duì)應(yīng)的預(yù)測(cè)序列后,計(jì)算各自平均相對(duì)誤差RME(n):

比較不同的RME(n),平均相對(duì)誤差最小時(shí)所對(duì)應(yīng)的滑動(dòng)參數(shù)取值是合理的。RME(n)的值反映了取不同滑動(dòng)參數(shù)時(shí)滑動(dòng)平均預(yù)測(cè)的結(jié)果與歷史數(shù)據(jù)的擬合程度,所以這種挑選方法是合理的。

2 基于滑動(dòng)平均的短時(shí)客流實(shí)時(shí)預(yù)測(cè)

2.1 基于滑動(dòng)平均法的短時(shí)客流實(shí)時(shí)預(yù)測(cè)

以每天為單位生成的原始客流時(shí)間序列受隨機(jī)因素影響,波動(dòng)強(qiáng)烈,呈現(xiàn)出明顯的非平穩(wěn)特征,但歷史客流數(shù)據(jù)在每天同一時(shí)段內(nèi)的數(shù)據(jù)具有相似性,其組成的時(shí)間序列起伏變化不會(huì)太大,可被視為變化較平穩(wěn)的時(shí)間序列。所以,由歷史客流時(shí)間序列每天同一時(shí)刻數(shù)據(jù)構(gòu)成的時(shí)間序列,用滑動(dòng)平均方法對(duì)下一天處于相同時(shí)間段數(shù)據(jù)進(jìn)行預(yù)測(cè),可得到基于歷史數(shù)據(jù)的預(yù)測(cè)客流時(shí)間序列,接下來(lái)根據(jù)實(shí)時(shí)客流數(shù)據(jù)進(jìn)行實(shí)時(shí)預(yù)測(cè)[10]。其方法簡(jiǎn)單、運(yùn)算速度快,又具有較好的預(yù)測(cè)精度。具體算法步驟如下:

步驟1 生成原始客流時(shí)間序列矩陣。

其中,N為每天生成的原始客流數(shù)據(jù)量,m為采集客流數(shù)據(jù)樣本的天數(shù)。m天歷史客流數(shù)據(jù)在每天同一時(shí)間段j的客流量所生成的新客流時(shí)間序列為:。

步驟2 確定用于滑動(dòng)平均的參數(shù)n j。參數(shù)n j＝2,3,…,m－1,計(jì)算n j取不同值時(shí)的滑動(dòng)結(jié)果:

不同的滑動(dòng)參數(shù)n j所對(duì)應(yīng)的預(yù)測(cè)平均相對(duì)誤差為:

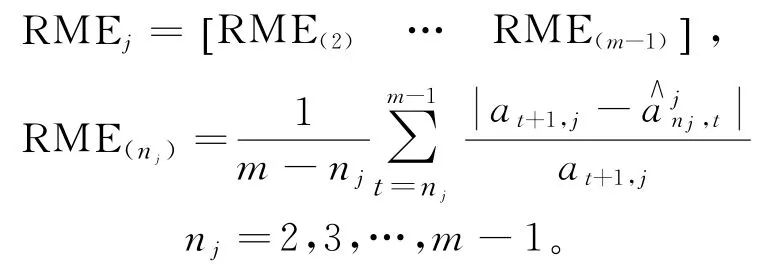
步驟3 采用滑動(dòng)平均法預(yù)測(cè)第m＋1天各時(shí)刻的客流量數(shù)據(jù)。將取值最小時(shí)的滑動(dòng)參數(shù)n j對(duì)應(yīng)的作為第m＋1天時(shí)刻j的客流量預(yù)測(cè)值,同理,可以得到第m＋1天的預(yù)測(cè)客流時(shí)間序列:

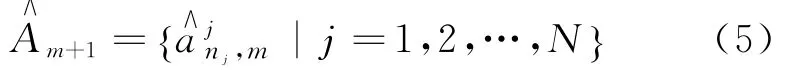
步驟4 基于實(shí)時(shí)客流數(shù)據(jù)對(duì)預(yù)測(cè)客流量進(jìn)行實(shí)時(shí)預(yù)測(cè)。實(shí)時(shí)預(yù)測(cè)結(jié)果為:

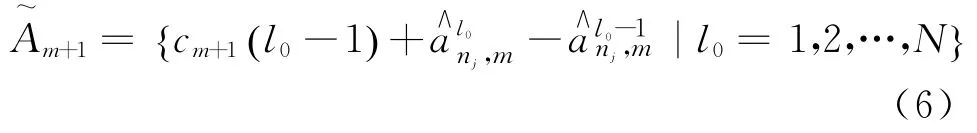
2.2 評(píng)價(jià)方法

本文擬采用平均相對(duì)誤差(RME)和均方根誤差(RMSE)這兩種方法來(lái)對(duì)算法預(yù)測(cè)的誤差效果進(jìn)行評(píng)價(jià)[11]。

2.2.1 RME

平均相對(duì)誤差用來(lái)評(píng)價(jià)預(yù)測(cè)客流數(shù)據(jù)與真實(shí)客流數(shù)據(jù)之間的相對(duì)誤差的平均值,其計(jì)算公式為:

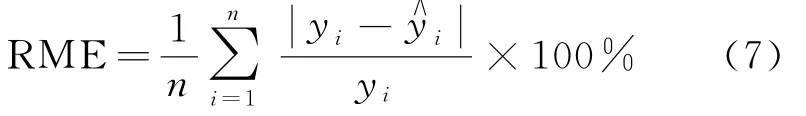
式中:y i為真實(shí)客流數(shù)據(jù);為對(duì)應(yīng)的預(yù)測(cè)客流數(shù)據(jù);n為每天采樣的客流數(shù)據(jù)量。

RME越接近于0,說(shuō)明客流預(yù)測(cè)精確度越高。

2.2.2 RMSE

均方根誤差用于評(píng)價(jià)預(yù)測(cè)客流數(shù)據(jù)與真實(shí)數(shù)據(jù)誤差平方和的均值平方根,其公式如下:

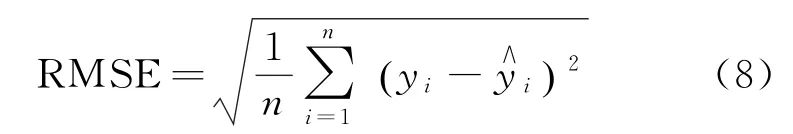
RMSE越接近于0,說(shuō)明客流預(yù)測(cè)算法越準(zhǔn)確。

3 實(shí) 驗(yàn)

基于本文提出的方法,針對(duì)2015年4月1日到29日上海地鐵一號(hào)線人民廣場(chǎng)站進(jìn)站和莘莊站進(jìn)站刷卡信息,分別采取5 min和15 min時(shí)間粒度采樣生成原始客流時(shí)間序列。由于運(yùn)營(yíng)時(shí)間不同,5 min粒度時(shí),人民廣場(chǎng)站每一個(gè)完整運(yùn)營(yíng)日將獲得212個(gè)進(jìn)站觀測(cè)值,莘莊站將獲得204個(gè)進(jìn)站觀測(cè)值;15 min粒度時(shí),人民廣場(chǎng)站每一個(gè)完整運(yùn)營(yíng)日將獲得70個(gè)進(jìn)站觀測(cè)值,莘莊站將獲得68個(gè)進(jìn)站觀測(cè)值。共獲得29天的原始客流數(shù)據(jù)。

實(shí)驗(yàn)首先通過(guò)最小平均相對(duì)誤差檢驗(yàn)方法確定滑動(dòng)平均參數(shù)n j,然后用式(5)得出最小平均相對(duì)誤差條件下第30天各時(shí)刻預(yù)測(cè)值。再根據(jù)實(shí)時(shí)客流數(shù)據(jù)用式(6)對(duì)預(yù)測(cè)結(jié)果處理,得到實(shí)時(shí)客流預(yù)測(cè)結(jié)果,并與支持向量機(jī)(SVM)、反向傳播神經(jīng)網(wǎng)絡(luò)(BPNN)、小波神經(jīng)網(wǎng)絡(luò)(WNN)和小波組合支持向量機(jī)(WS)4種算法預(yù)測(cè)客流量誤差進(jìn)行比較。

3.1 人民廣場(chǎng)地鐵站進(jìn)站客流預(yù)測(cè)

2015年4月1日人民廣場(chǎng)地鐵站進(jìn)站客流經(jīng)過(guò)5 min和15 min采樣后得到客流時(shí)間序列如圖1所示。圖2為采用滑動(dòng)平均方法預(yù)測(cè)4月30日5:45～5:50、6:00～6:15這兩個(gè)時(shí)間段內(nèi)客流量時(shí),選取不同的滑動(dòng)參數(shù)n j進(jìn)行預(yù)測(cè)所對(duì)應(yīng)的平均相對(duì)誤差。基于實(shí)時(shí)交通客流數(shù)據(jù),通過(guò)滑動(dòng)平均方法,得到4月30日的5 min粒度和15 min粒度預(yù)測(cè)客流時(shí)間序列,其結(jié)果如圖3所示。幾種不同預(yù)測(cè)方法的實(shí)驗(yàn)誤差見(jiàn)表1。

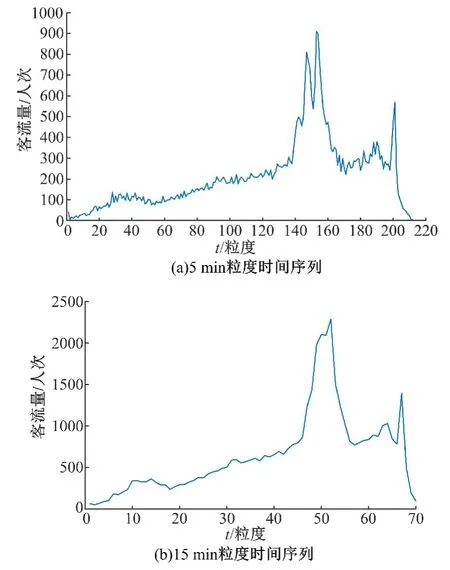
圖1 2015年4月1日人民廣場(chǎng)進(jìn)站客流5 min和15 min粒度時(shí)間序列Fig.1 Entrance passenger flow time series with 5 min and 15 min at People’square station on April 1st,2015

圖2 預(yù)測(cè)不同時(shí)間段客流量時(shí)不同n j對(duì)應(yīng)的RMEFig.2 RME corresponding to different n j while predicting the passenger flow between 5:45～5:50 and 6:00～6:15

圖3 2015年4月30日人民廣場(chǎng)站進(jìn)站實(shí)時(shí)預(yù)測(cè)客流5 min和15 min粒度時(shí)間序列Fig.3 Real-time forecast of entrance passenger flow time series with 5 min and 15 min at People’square station on 30th April,2015

表1 2015年4月30日人民廣場(chǎng)進(jìn)站客流預(yù)測(cè)結(jié)果比較表Table 1 Comparison between predicted entrance passenger flows at People’s square station on April 30th,2015

通過(guò)表1對(duì)人民廣場(chǎng)站進(jìn)站短時(shí)客流預(yù)測(cè)結(jié)果分析可以發(fā)現(xiàn),基于滑動(dòng)平均法的實(shí)時(shí)客流預(yù)測(cè)精度最高,且計(jì)算耗時(shí)也遠(yuǎn)遠(yuǎn)少于其他方法。從圖1和2可以看出,采取15 min粒度采樣生成的原始客流時(shí)間序列更平滑,故預(yù)測(cè)15 min粒度的客流序列的平均相對(duì)誤差更小。從圖2可以看出,預(yù)測(cè)不同時(shí)間段的客流量所采用的滑動(dòng)參數(shù)是依據(jù)預(yù)測(cè)RME最小標(biāo)準(zhǔn)自適應(yīng)選取的。對(duì)比圖3(a)(b)可知,在晚高峰時(shí)段客流數(shù)據(jù)波動(dòng)強(qiáng)烈,導(dǎo)致擬合效果稍差。而本文提出的基于實(shí)時(shí)客流數(shù)據(jù)的滑動(dòng)平均預(yù)測(cè)方法對(duì)晚高峰波動(dòng)較強(qiáng)烈的數(shù)據(jù)具有較好預(yù)測(cè)效果。

3.2 莘莊地鐵站進(jìn)站客流預(yù)測(cè)

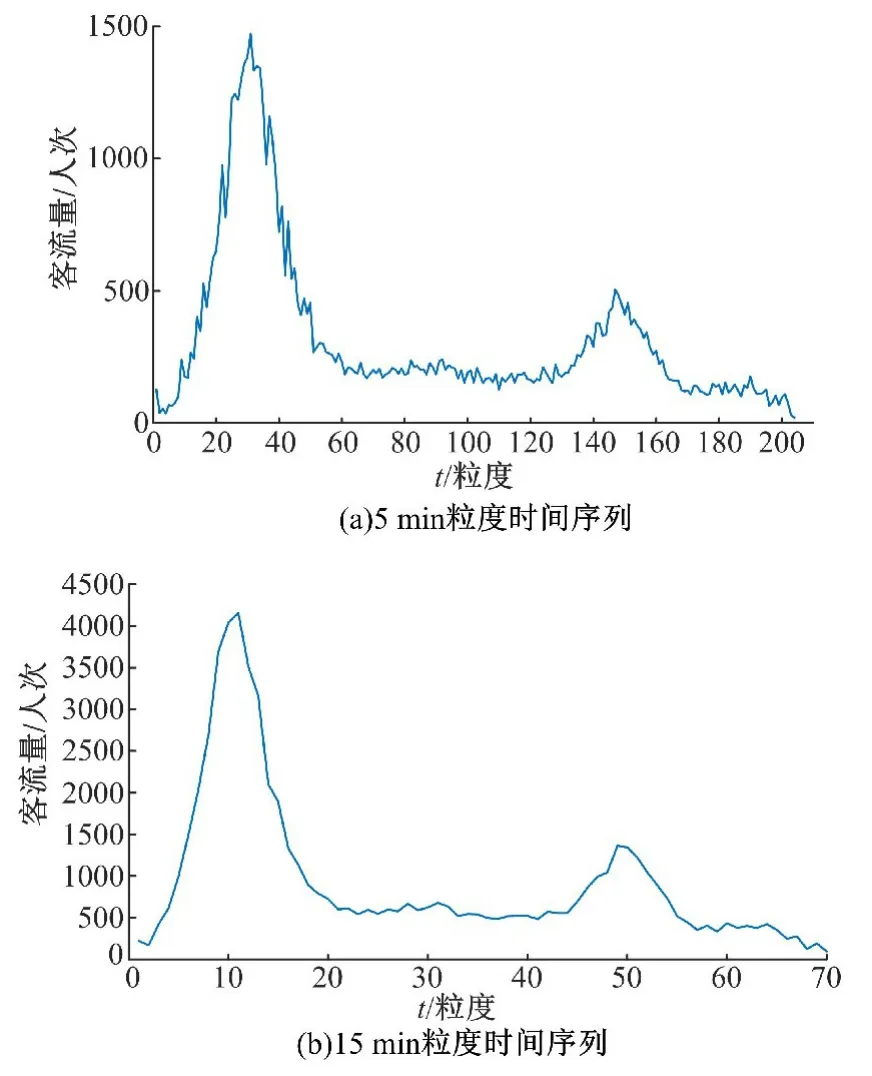
圖4 2015年4月1日莘莊站進(jìn)站客流5 min和15 min粒度時(shí)間序列Fig.4 Entrance passenger flow time series with 5 min and 15 min at Xinzhuang station on April 1st,2015

圖5 預(yù)測(cè)不同時(shí)間段客流量時(shí)不同n j對(duì)應(yīng)的RMEFig.5 RME corresponding to different n j while predicting passenger flow between 6:00～6:05 and 9:15～9:30

2015年4月1日上海市地鐵一號(hào)線莘莊進(jìn)站客流經(jīng)5 min粒度和15 min粒度采樣得到原始客流時(shí)間序列如圖4所示。圖5(a)(b)分別為采用滑動(dòng)平均方法預(yù)測(cè)4月30日6:00～6:05、9:15～9:30這兩個(gè)時(shí)段客流時(shí),取不同滑動(dòng)參數(shù)n j進(jìn)行預(yù)測(cè)對(duì)應(yīng)的平均相對(duì)誤差。采用與實(shí)驗(yàn)1同樣方法得到4月30日5 min粒度和15 min粒度預(yù)測(cè)客流時(shí)間序列如圖6所示。幾種不同方法的預(yù)測(cè)誤差見(jiàn)表2。

圖6 2015年4月30日莘莊站進(jìn)站實(shí)時(shí)預(yù)測(cè)客流5 min和15 min粒度時(shí)間序列Fig.6 Real-time forecast of entrance passenger flow time series with 5 min and 15 min at Xinzhuang station on 30th April,2015

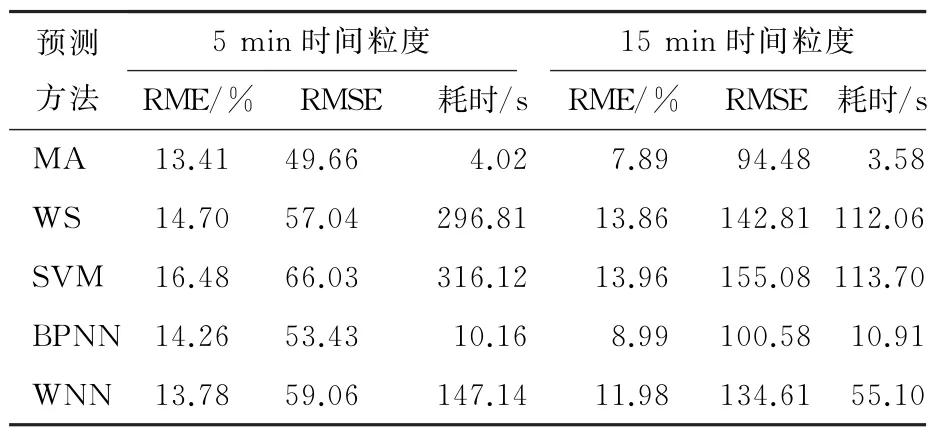
表2 2015年4月30日莘莊站進(jìn)站客流預(yù)測(cè)結(jié)果比較表Table 2 Comparison between predicted entrance passenger flows at Xinzhuang Station on April 30th,2015

通過(guò)表2對(duì)莘莊站進(jìn)站短時(shí)客流預(yù)測(cè)結(jié)果分析可以發(fā)現(xiàn),基于實(shí)時(shí)交通客流的滑動(dòng)平均預(yù)測(cè)方法精度高于其他4種預(yù)測(cè)方法,且運(yùn)算時(shí)間優(yōu)于其他方法。從圖4可看出,15 min粒度采樣生成的原始客流時(shí)間序列更平滑,波動(dòng)性減弱,預(yù)測(cè)精度比5 min粒度的提高很多。對(duì)比圖6(a)(b)可以發(fā)現(xiàn),在波動(dòng)強(qiáng)烈的早高峰時(shí)段,預(yù)測(cè)算法的擬合效果也較好,故本文提出的基于實(shí)時(shí)交通數(shù)據(jù)的滑動(dòng)平均方法對(duì)早高峰客流數(shù)據(jù)也具有較好的預(yù)測(cè)效果。

4 結(jié)束語(yǔ)

針對(duì)軌道交通客流歷史數(shù)據(jù)在每天相同時(shí)段內(nèi)具有一定相似性的特點(diǎn),以及當(dāng)前應(yīng)用于短時(shí)客流預(yù)測(cè)領(lǐng)域算法復(fù)雜、計(jì)算速度慢的不足,本文將算法簡(jiǎn)單、計(jì)算速度快的滑動(dòng)平均方法應(yīng)用于軌道交通短時(shí)客流領(lǐng)域。通過(guò)采用滑動(dòng)平均算法對(duì)人民廣場(chǎng)站和莘莊站兩站點(diǎn)進(jìn)站客流進(jìn)行預(yù)測(cè)并驗(yàn)證。結(jié)果表明,本文提出的基于滑動(dòng)平均算法的實(shí)時(shí)客流預(yù)測(cè)方法精度高于非線性預(yù)測(cè)方法支持向量機(jī)、BP神經(jīng)網(wǎng)絡(luò)和小波神經(jīng)網(wǎng)絡(luò),也明顯高于小波和支持向量機(jī)的組合預(yù)測(cè)方法。同時(shí),滑動(dòng)平均方法還具有算法簡(jiǎn)單、計(jì)算速度快的優(yōu)點(diǎn),具有較好的預(yù)測(cè)效果。

[1]裴益軒,郭民.滑動(dòng)平均法的基本原理及應(yīng)用[J].火炮發(fā)射與控制學(xué)報(bào),2001(1):21-23.Pei Yi-xuan,Guo Min.The fundamental principle and application of sliding average method[J].Gun Launch&Control Journal,2001(1):21-23.

[2]胡松,江小煒,楊光,等.滑動(dòng)平均濾波在微弱脈沖信號(hào)檢測(cè)中的應(yīng)用[J].計(jì)算機(jī)與數(shù)字工程,2007,35(10):169-172.Hu Song,Jiang Xiao-wei,Yang Guang,et al.Using of moving average filter in faint pulse signal detection[J].Computer and Digital Engineering,2007,35(10):169-172.

[3]何耀,劉興濤,張陳斌,等.基于動(dòng)力電池組內(nèi)阻模型的絕緣檢測(cè)算法[J].吉林大學(xué)學(xué)報(bào):工學(xué)版,2013,43(5):1165-1170.He Yao,Liu Xing-tao,Zhang Chen-bin,et al.Insulation detection algorithm for high-power battery system based on internal resistance model[J].Journal of Jilin University(Engineering and Technology Edition),2013,43(5):1165-1170.

[4]Hatchett R B,Brorsen B W,Anderson K B.Optimal length of moving average to forecast futures basis[J].Journal of Agricultural and Resource Economics,2009,35(1):18-33.

[5]Shih Y T,Cheng H M,Sung S H,et al.Application of the N-Point moving average method for brachial pressure waveform-derived estimation of central aortic systolic pressure[J].Hypertension,2014,63(4):865-870.

[6]潘紅宇.時(shí)間序列分析[M].北京:對(duì)外經(jīng)濟(jì)貿(mào)易大學(xué)出版社,2015.

[7]Dhuyvetter K C,Kastens T L.Forecasting crop basis:practical alternatives[C]∥Proceedings of the NCR-134 Conference on Applied Commodity Price Analysis,Forecasting,and Market Risk Management,Chicago,USA,1998:49-67.

[8]Hatchett R B.Optimal length of moving averages to use when forecasting basis[D].Stillwater Ok:Department of Agricultural Economics,Oklahoma State University,2009.

[9]楊林泉.預(yù)測(cè)與決策方法應(yīng)用[M].北京:冶金工業(yè)出版社,2011.

[10]劉寒冰,李國(guó)恒,譚國(guó)金,等.基于時(shí)間序列的邊坡位移實(shí)時(shí)預(yù)測(cè)方法[J].吉林大學(xué)學(xué)報(bào):工學(xué)版,2012,42(增刊1):193-197.Liu Han-bing,Li Guo-heng,Tan Guo-jin,et al.Real-time prediction method of slop displacement based on time series analysis[J].Journal of Jilin University(Engineering and Technology Edition),2012,42(Sup.1):193-197.

[11]楊軍.地鐵客流短時(shí)預(yù)測(cè)及客流疏散模擬研究[D].北京:北京交通大學(xué)電子信息工程學(xué)院,2013.Yang Jun.Research on metro passenger flow shorttime prediction and evaluation simulation[D].Beijing:School of Electronic and Information Engineering,Beijing Jiaotong University,2013.