基于CFD的超大型液化氣船型線優化

，，

(中國船舶工業集團公司第七○八研究所，上海 200011)

近年來，超大型液化氣船市場需求日漸增長，從世界商船隊保有量上看以DWT計2016年全年較2015年增幅最大的是液化氣運輸船。超大型液化氣船一般以中高速為主，船東營運過程中往往存在多個航速點和吃水工況。該船型在單一設計航速下的性能指標已不能滿足船東多工況營運的需求，船東對新設計船的多工況點兼顧的優化設計愈發重視[1- 2]。為此，對某超大型液化氣船2種不同風格的艏部形式(傳統球鼻形艏部與直立楔形艏)進行計算分析。首先結合CAESES優化平臺和RAPID勢流計算軟件，采用改進的遺傳算法NSGA- II分別對2種風格的球首進行了自動優化計算，得到基于目標函數(不同工況下的興波阻力系數Cw)的Pareto最優解集。然后分別從Pareto解集中選取優化后的線型，采用粘流計算軟件STAR- CCM+進行了總阻力對比。最終選取直立楔形艏線型進行了船模試驗驗證。在對線型研究的同時，提出適用于工程實際的優化設計流程。

1 船型尺度及特征

超大型液化氣船往往為中高速船型，其興波阻力成分占總阻力比例較大。進一步的，通常艏部型線對興波成分具有較大影響。因此本文研究時僅考慮艏部的型線優化。

1.1 主尺度和參數

本船為某84 000 m3級超大型全冷式液化氣船，A型貨罐，艉機型。主尺度和參數如下。

總長Loa=227.0 m；

垂線間長LPP=223.5 m；

型寬B=36.6 m；

設計吃水Td=11.4 m；

設計航速Vs=16.8 kn。

1.2 艏部特征

選取2種不同風格的艏部作為本船初始線型進行優化對比，艏部特征對比見圖1。其一為傳統形式的球鼻艏，如圖1a)左所示，球鼻艏在液化氣船型上較為常見，主要性能特征體現在高速段能較好地改善興波，但對不同吃水和低速段的兼顧性不一定好；其二為直立楔形艏，其側面輪廓為直立型，而橫向為楔形的扁平狀，如圖1b)所示，其水線進流角很小，其壓載吃水下的阻力性能一般會比較好，關于這一點下文會有進一步的計算驗證。

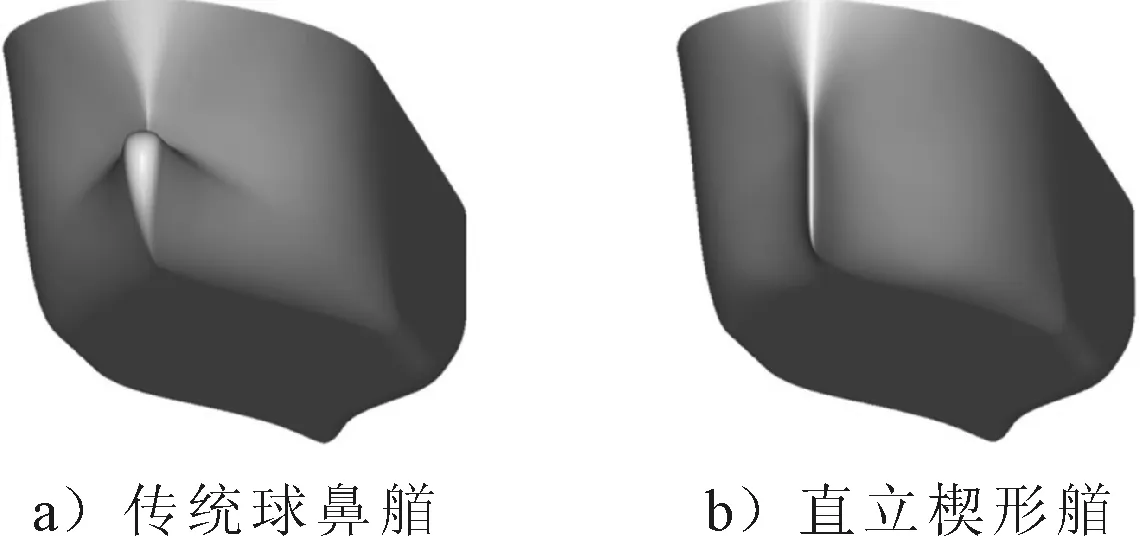
圖1 艏部特征對比

2 型線優化

2.1 優化流程

本船型線優化時船東要求考察設計吃水和壓載吃水下多個工況點的阻力性能。針對艏部優化，當前勢流方法已具備相當的準確性[3- 6]，擬采用勢流軟件RAPID結合CAESES優化平臺進行艏部的自動優化。根據經驗勢流軟件往往在壓載工況下會出現不收斂的情況，而采用自動優化手段評估其壓載工況的效果有限，且本船優化時考慮到船東實際營運過程中對設計吃水下兩個航速的切實關注，本文仿真優化流程將分為前后兩個階段。

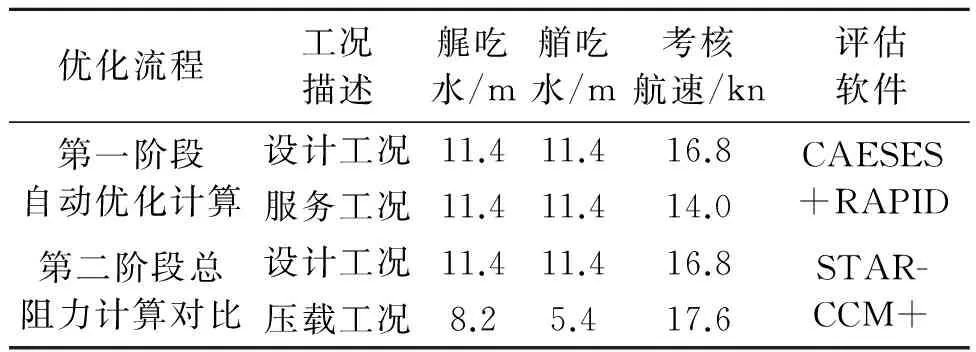
表1 仿真優化流程

2.2 第一階段：自動優化計算

由于第一階段優化為2種不同的艏部并行進行計算，并且過程類似，因此以下內容僅以直立楔形艏為例說明。

2.2.1 設計變量及目標函數

針對直立楔形艏，選取3個控制參數作為設計變量，并且列出了其上下限變化范圍，見表2和圖2。

表2設計變量m

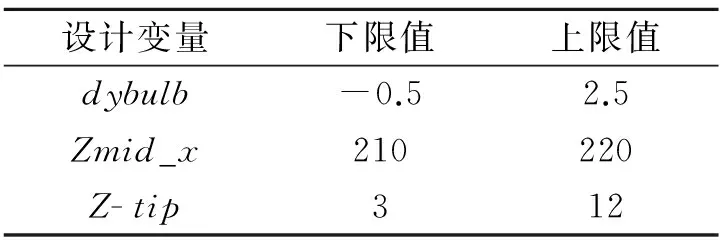
設計變量下限值上限值dybulb-0.52.5Zmid_x210220Z-tip312

表中，dybulb為艏部區域最大剖面半寬變化量(y坐標值)，表征艏部區域胖瘦的參數；Zmid_x為艏部區域最大剖面沿船長方向的位置(x坐標值)，表征最大剖面的縱向分布的參數；Z_tip為隱形艏剖面最前點的高度(z坐標值)，表征艏部形式的翹平度的參數。

圖2 設計變量示意

需要特殊說明的是，最大剖面半寬趨勢線由CAESES的feature definition建立，它與Z_tip存在一定的幾何函數關系，因此Z_tip可以表征隱形艏的上翹程度。

取設計吃水2個航速下的興波阻力系數作為其目標函數，分別為11.4 m/16.8 kn下的興波阻力系數Cw1和11.4 m/14 kn下的興波阻力系數Cw2。優化結果應使得Cw1和Cw2均達到最小，因此這是一個典型的多目標優化問題。

為得到合理的線型并且不影響船舶總布置，必須對船體變形區域進行一定的約束控制，設置船舶在設計吃水下的排水體積作為自動變形的約束變量。該值上下浮動設置為不超過400 m3。

2.2.2 改進的非劣分類遺傳算法NSGA- II

多目標優化中，由于存在目標之間的沖突和無法比較的現象，一個解在某個目標上是最好的，在其他的目標上可能比較差。多目標優化問題中Pareto最優解僅為其一個可以接受的非劣解，另一方面，多目標優化問題通常都具有多個最優解。因此多目標優化問題的設計關鍵在于求取Pareto最優解集。

NSGA- Ⅱ是目前最流行的多目標進化算法之一，它降低了非劣排序遺傳算法的復雜性，具有運行速度快、解集收斂性好的優點，成為其他多目標優化算法性能的基準。NSGA- Ⅱ算法是Srinivas和Deb于2000年在NSGA的基礎上提出的，它比NSGA算法更加優越：采用快速非支配排序過程、精英保留策略和無參數小生境操作算子，克服了傳統、NSGA算法的計算復雜度高、非精英保存策略和需要特別指定共享半徑的缺點，使準Pareto域中的個體能擴展到整個Pareto域，并均勻分布，保持了種群的多樣性[5]。主要特點體現如下。

1)不需要用戶指定一些類似Fitness sharing方法中niche count(小生境大小)之類的參數。這些參數的輕微不同有可能導致結果很大的差異，所以用戶主觀指定的參數越少越好。

2)非支配集排序(non- dominated sorting)的時間復雜度相對其他算法較低。已有的排序方法時間復雜度為O(M·N3)(M為目標函數個數；N為種群個體數目)，NSGA- Ⅱ的排序方法時間復雜度為O(M·N2)。

3)維護了精英個體。維護精英個體能明顯地提高多目標GA的效果。

本文計算采用NSGA- II算法，種群數設置為20，算法迭代次數為16，突變概率為0.06，交叉概率為0.9。

2.2.3 自動優化計算結果

采用NSGA- Ⅱ優化算法，迭代次數320次，耗時525 min，得到以dybulb，Z_tip，Zmid_x為設計變量，以Cw1，Cw2為目標函數的計算結果。圖3～圖6為各控制參數運行時歷。

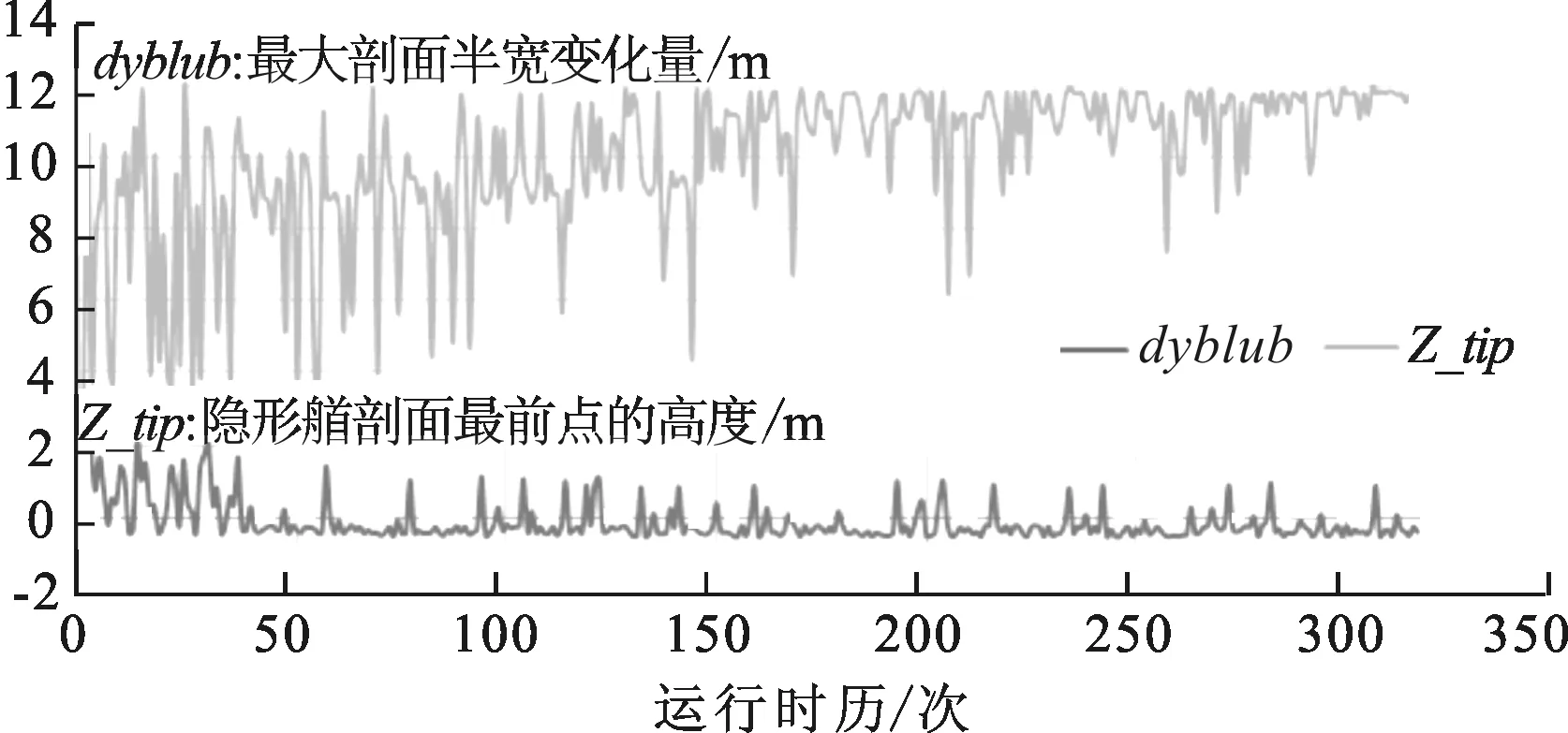
圖3 設計變量運行時歷(dybulb，Z_tip)

圖4 設計變量運行時歷(Zmid_x)

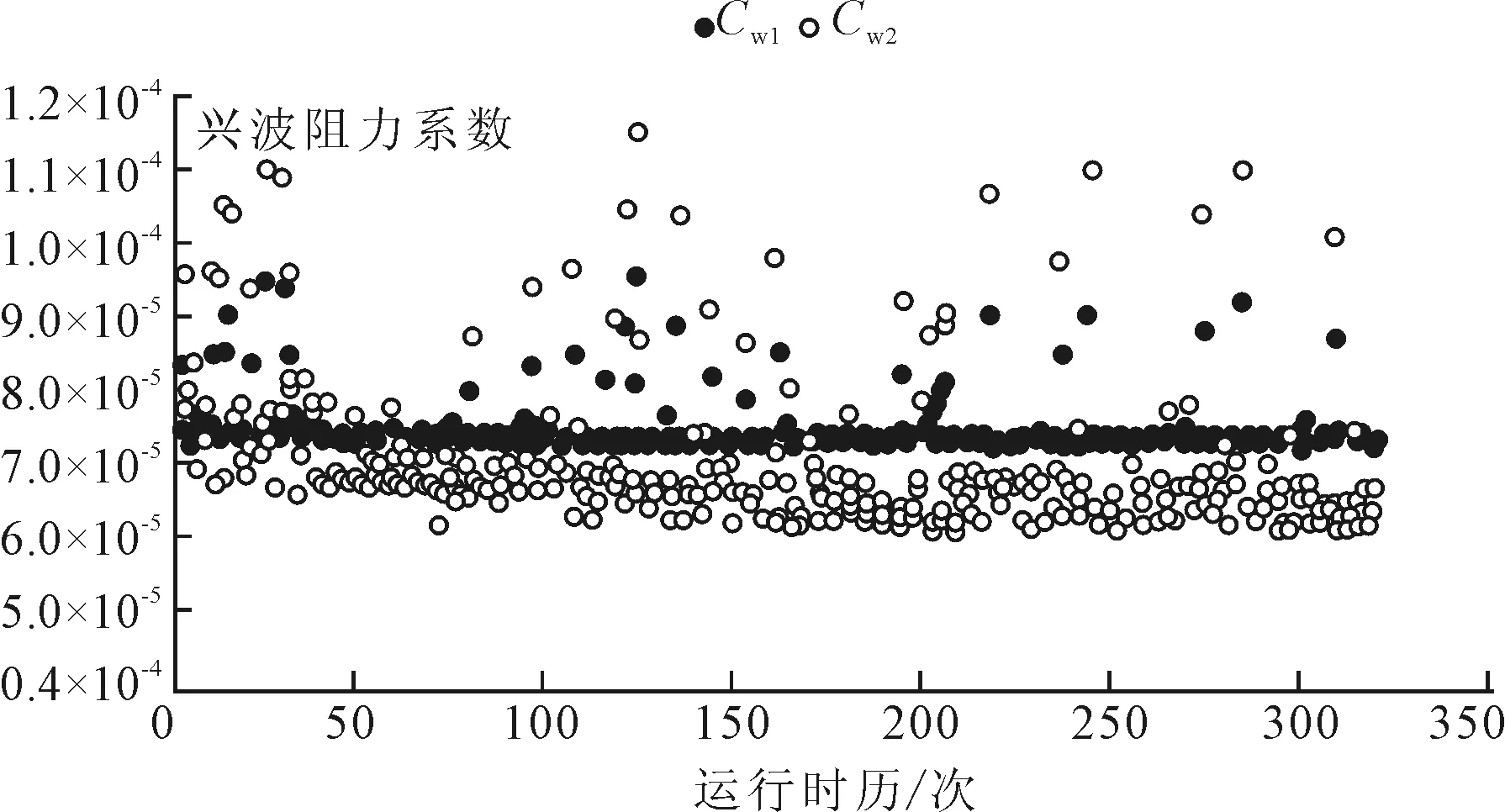
圖5 目標函數Cw1、Cw2運行時歷

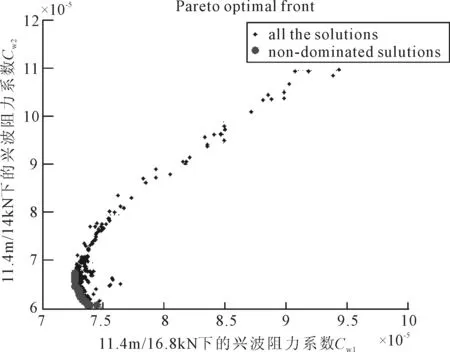
圖6 目標函數Cw1、Cw2的Pareto最優解集

由圖5可見，興波阻力系數在改進的遺傳算法優化下不斷減小并逐步趨于穩定，而我們亦可以看出，NSGA- Ⅱ算法收斂速度較快。

圖6中灰色部分的點(左下角區域)組成的區域即為計算得到的關于服務工況和設計工況下興波阻力系數的Pareto最優解集，其中存在多個非劣解[6]。從Pareto最優解集中選出符合本船實際需求的解作為優化后的線型。提取相關數據可以發現，優化后的船舶興波阻力系數較之初始線型在設計航速下減小了2.09%，在服務航速下減小了7.72%。對于本船來講，弗汝德數在0.2以上，其興波阻力成分占比較大，興波阻力的有效優化將反應到總阻力的降低。

船舶主要控制參數及目標函數在優化前后的對比見表3。

表3 控制參數及計算效果前后對比

由表3可見，優化型線的最大剖面半寬(dybulb)較之原型略瘦，球艏最大剖面位置(Zmid_x)后移，艏部最前點(Z-tip)上翹。這些變化綜合起來起到了降低興波阻力性能的效果。據此可以得出結論，針對直立楔形艏的阻力優化，其艏部前端高度應略上翹，其最大剖面縱向位置不宜過于靠前，對于本例為92%～93%LPP為優，同時應保證最大剖面不要過大。

對優化過程的所有設計變量進行主成分分析[7]，可以得到圖7。圖中“O”狀點集為開始的160個算例，“x”狀點集為后面的160個算例，可以看到在優化的初始階段，“O”狀點集較多的沿Zmid_x變量分布，而沿dybulb的分布比較分散且平均，這說明在優化進程的初始階段Zmid_x亦即最大剖面的縱向分布影響較大。而后160個算例中，“x”狀點集中的分布在Z_tip附近，說明在優化進程的后半部分Z_tip亦即表征艏部翹平度的參數影響較大。根據圖7的主成分分析，可以分析出優化算法在優化的前期主要考察最大剖面的縱向分布，同時兼顧對最大剖面胖瘦的變化考察，待趨勢穩定后逐漸轉向對艏部前點翹平度的局部變化考察，可以據此得到后續優化設計時的調整思路，從而進一步提高優化效率。本文提出的這一分析思路結合了統計分析方法中的主成分分析方法，在多參數優化時具有一定的借鑒意義。

以設計航速下的波形分布對比為例(見圖8)，可以看出優化后的線型其波形分布要優于初始線型，艏部波峰區和肩部的波谷區域均得到有效的改善，另外在船舯部位波形明顯平坦許多，從而印證了阻力系數的變化趨勢是正確的。

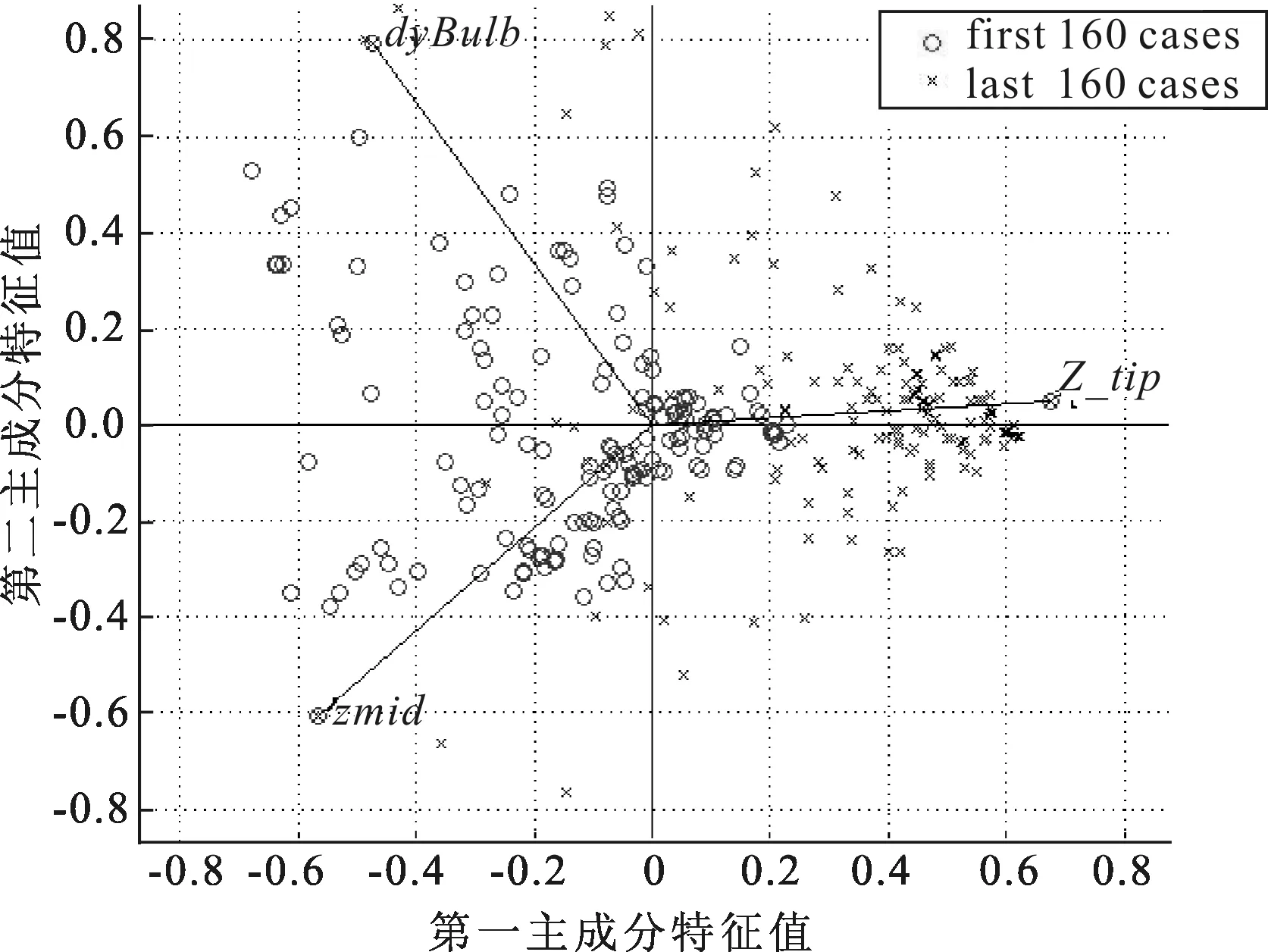
圖7 控制參數的主成分分析

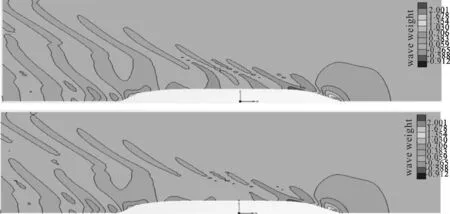
圖8 設計航速的波形分布對比

2.3 第二階段：總阻力計算驗證

根據前面的分析，對直立楔形艏和傳統球鼻艏兩種風格的球艏并行進行關于艏部的自動優化選型，由此得到2個不同風格的艏部型線的優化結果。采用STAR- CCM+粘流計算軟件對這2個線型進行了總阻力計算對比，該軟件網格劃分功能十分強大，對于不同類型船舶，只要替代原流場網格的船體便可劃分出與原始網格形式及數量相當的新網格。在需要精確描述流場的地方單獨添加較密的長方體或其他形狀的網格塊[12]。因此該軟件在保證計算精度的同時可以節省計算時間。對于本文來講，艏部風格不同，計算時需對艏部網格進行加密，同時采用三維非定常分離隱式求解器，使用二階時間離散格式，并在出口處設置消波區[8]。

計算工況為設計工況和壓載工況，結果見表4。

表4 粘性流計算結果對比 %

表4為換算到實船的有效功率Pe對比值。在壓載工況下，直立楔形艏的阻力值則較多的好于傳統球艏。可以推測這是因為在壓載工況下直立楔形艏在水線處進流角較小，能夠有效地減小破波、碎波的影響，因此阻力性能優于傳統球鼻艏；而在設計吃水下由于其隱形艏的作用，仍然具有較強的興波疊加作用，從而降低整體的阻力，使得設計工況下兩者的差別并不太大。

圖9是基于STAR- CCM+軟件計算后得到的計算波形對比，可以發現直立楔形艏在壓載工況下其興波波形要遠好于傳統球鼻艏線型，恰好證明了前面結論的正確性。

圖9 優化后：傳統球鼻艏線型(左)與直立楔形艏(右)線型的波形分布對比

3 船模試驗驗證

由于船東要求在優化時需兼顧考慮壓載航行下的阻力性能，而直立楔形艏在壓載工況下阻力特性良好，因此本船最終選取該線型作為最終船模試驗線型，并于2015年在708所的拖曳水池進行了相關船模試驗。試驗結果在設計工況下滿足設計規格書要求，在壓載工況下航速較預期提高約1.7%，這一試驗結果和CFD分析結論保持了一致性。見圖10。

其中各分圖為：側視圖(上)，斜艏視圖(左下)，正視圖(右下)

圖10 采用直立楔形艏進行船模試驗

4 結論

1)引入一種新型艏部形式- 直立楔形艏，通過計算分析得到了該形式的艏部基本特性。該艏部形式應用于超大型液化氣船上是較新的應用案例，通過模型試驗，驗證了該線型的阻力特性滿足設計要求。

2)通過與傳統球鼻艏計算對比可知，直立楔形艏在壓載工況下由于其水線較長且進流角很小，因此其阻力性能較好。通過自動型線優化，可以保證其設計工況下阻力性能仍和傳統球鼻艏保持相當，而壓載工況下的優越性將使其受到青睞。

3)提出了適用于前期研發的線型優化完整流程。項目初期采用勢流計算軟件加參數化模型優化平臺進行自動優化，根據興波阻力系數篩選優化線型；待線型確定后使用粘流計算軟件對比總阻力效果，最終完成線型優化的迭代。

[1] 劉英良.超大型集裝箱船多工況點的最佳方形系數范圍探索[J].船舶,2014(1):21- 4.

[2] 劉英良.基于cfd的超大型集裝箱船線型優化研究[D].北京：中國艦船研究院,2014.

[3] 蔡榮泉.關于船舶cfd的現狀和一些認識[J].船舶,2002(1):29- 37.

[4] 張寶吉.船體線型優化設計方法及最小阻力船型研究[D].大連理工大學,2009.

[5] DEB K, PRATAP A, AGRAWAL S, et al. A fast and elitist multiobjective genetic algorithm: Nsga- Ii[J]. Ieee transactions on evolutionary computation,2002,6(2):182- 97.

[6] 李學斌,張蓓,盧兵.多目標進化算法在船型方案設計中的應用[J].船海工程,2008(2):1- 3.

[7] 陳雅菊.基于多目標遺傳算法和主成分分析的船型主尺度論證[J].船海工程,2015(2):31- 5.

[8] 蔣武杰,呂永峰,陳京普,等.雙艉鰭油船的波浪增阻數值模擬研究[C].Proceedings of The第十三屆全國水動力學學術會議暨第二十六屆全國水動力學研討會.山東,青島,F,2014.