薄板-附加阻尼層復合結構振動模態特性試驗研究與仿真分析

王 超，呂振華，顧葉青，呂毅寧

（1.南京電子技術研究所，南京 210039； 2. 清華大學 汽車工程系，北京 100084）

降低車身結構振動與車內噪聲水平是提高車輛動態舒適性和客戶滿意度的重要方法。在汽車的設計與開發中，NVH性能要求貫穿于車身結構設計的全過程。目前多數車身結構都是由薄鋼板經沖壓焊接而成，該類薄板結構的阻尼損耗因子一般較低，通常只有5×10-3左右[1]。因此，振動響應較大處的車身薄板結構通常還需附加結構阻尼處理，以衰減來自動力總成、排氣與傳動系統、懸架系統等向車身結構傳遞的振動，從而通過降低車身薄板的振動來減小車內噪聲。

車身等復雜的薄板結構上常用的附加阻尼處理方法包括如圖1所示的自由結構阻尼和約束結構阻尼兩種形式。結構阻尼的具體處理方式包括粘結型阻尼、熱熔型阻尼、噴涂型阻尼、局部約束型阻尼以及復合材料約束阻尼結構等[2-4]。

圖1 兩種典型的阻尼結構形式

對阻尼層的布置進行優化設計可顯著改善車身等薄板結構的振動性能。研究表明，拓撲優化方法是對阻尼結構布置進行優化設計的有效方法[5]。準確獲取阻尼材料的力學參數和對薄板-附加阻尼層復合結構進行精確建模是對阻尼結構進行優化設計的基礎，王超等[6-7]已對阻尼材料力學參數的測試技術進行了深入研究，本研究重點探討薄板-阻尼層復合結構的有限元建模技術和分析方法。先對薄板-附加自由阻尼層復合結構的動態特性進行試驗分析，再對薄板-附加自由阻尼層復合結構的有限元建模技術進行研究；然后進一步研究了薄板-附加約束阻尼層復合結構的建模技術；最后對薄板-附加阻尼層復合結構的動態特性有限元分析方法進行了深入研究。

1 薄板- 附加自由阻尼層復合結構振動模態試驗分析

通過試驗分析可以掌握該類薄壁件－附加阻尼層復合結構的基本振動特性，并為薄板－附加自由阻尼層復合結構的有限元分析方法提供試驗依據。

1.1 試件設計

車身等薄壁件上附加結構阻尼可以有效改善由車身結構振動（小于200 Hz）引起的車內噪聲，據此設計了低階頻率在此頻率范圍內的兩種不同厚度規格的試件。試件1：500 mm×500 mm×0.7 mm薄鋼板中央位置粘貼420 mm×420 mm×2 mm的某一熱熔型阻尼材料；試件2：500 mm×500 mm×1.6 mm薄鋼板的中央位置粘貼420 mm×420 mm×4 mm的某一熱熔型阻尼材料。

1.2 試驗工況設計

（1）對試件的四個頂點進行固支約束（簡稱FPGZ）。該約束方式如圖2所示，約束試件前應對安裝試件的四個加載平臺的高度進行調平。

圖2 四點固支邊界條件下的試驗圖

（2）對試件的四邊進行固支約束（簡稱FSGZ）。為實現該約束狀態，合理設計了一個安裝支架，組成安裝支架的四個槽鋼都是由5 mm厚的鋼板折彎而成，該工況下試件的約束形式如圖3所示。

圖3 四邊固支邊界條件下的試驗圖

（3）對試件的兩邊進行固支約束（簡稱TSGZ）。將四邊固支條件下安裝支架的兩個短槽鋼拆除，即可對試件施加如圖4所示的兩邊固支的約束條件。

圖4 兩邊固支邊界條件下的試驗圖

1.3 測試系統及測點布置

1.3.1 測試系統介紹

試驗用PCB333B32單向和PCB356A16三向振動加速度傳感器、PCB 086C03力錘、LMS Mobile 05數據采集器等測試設備，建好的測試系統如圖2所示。

1.3.2 測點布置

試件上布置了如圖5所示的25個測點，試驗中為了減小加速度傳感器的附加質量對系統的影響，采取了多測點分批次測量的方法。

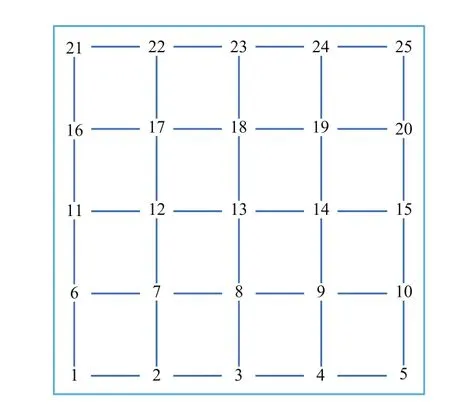
圖5 測點的布置

1.3.3 測試結果分析

試驗中對設計的安裝支架固有振動特性進行了分析，測得該支架的第一階固有頻率為268.6 Hz，這說明分析兩試件在200 Hz以下的振動特性是合適的。此外，由于阻尼材料多用于改善因低頻的結構振動引起的振動噪聲，所以表1只列出了各邊界條件下兩試件的低階固有振動特性。可見，不同的邊界條件對薄板－附加自由阻尼層復合結構振動特性的影響較大，四點固支邊界條件下，結構的固有振動頻率及損耗因子都較低。相對于1.6 mm厚的基礎層薄板試件2，0.7 mm厚的基礎層薄板的試件1具有更好的耗能特性。產生這種現象的主要原因是基礎層薄板厚度較小時，外部的低頻激勵更容易使其產生較大幅度的運動，在其表面附加自由阻尼層后，阻尼材料通過拉伸變形消耗的振動能量會較大，進而產生較大的模態損耗因子。車身上多數薄板結構的厚度與試件1相近，因此可以認為試件1的耗能特性更接近車身－附加阻尼層復合結構的振動特性。

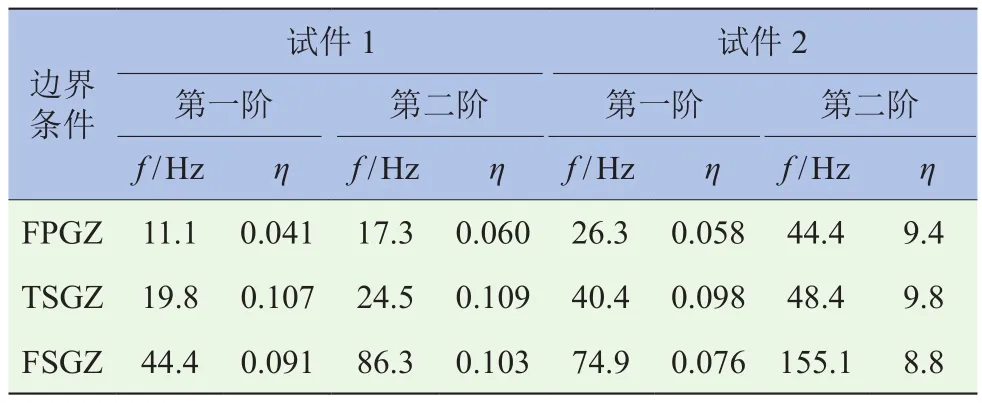
表1 三種邊界條件下兩試件的固有振動特性

2 薄板-附加自由阻尼層復合結構有限元建模技術及振動模態計算分析

2.1 有限元建模方法

根據薄板－附加自由阻尼層復合結構的特點，可選用兩層偏置板殼單元對其建模[8]，該單元通過數值插值方式使兩層板殼結構連接表面的變形協調一致。該模型需合理設置板殼單元的法向和偏移量，主要包括以下兩種情況：當一層板殼單元的法向指向另一層板殼單元時，偏移量需設為負值；當一層板殼單元的法向背離另一層板殼單元時，偏移量應設為正值。兩種情況下偏移量的絕對值都等于板殼單元厚度的一半，建好偏置單元的法向和偏移量后，使兩層殼單元在界面處的變形一致，該模型簡稱為OSOS模型。自由阻尼復合結構另一種常見的建模方法是分別采用偏置板殼單元和六面體單元模擬薄板和阻尼層，兩種單元在界面處的變形一致，該模型簡稱為OSH模型。薄板－附加自由阻尼層復合結構有限元模型的兩種建模方法如圖6所示。

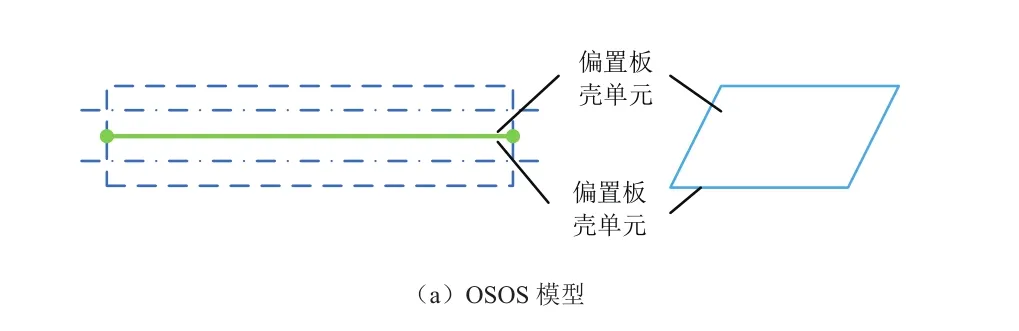
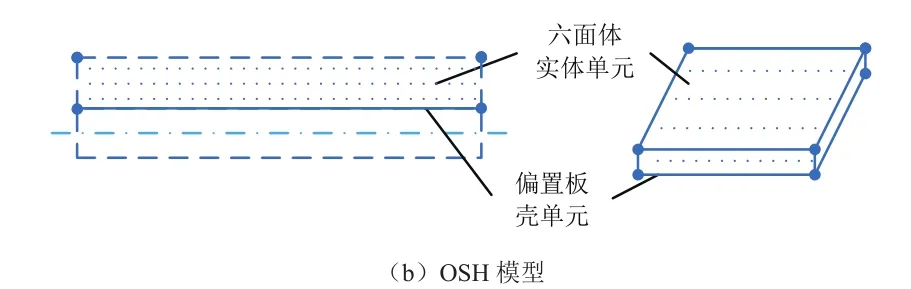
圖6 附加自由阻尼層復合結構的兩種有限元建模方法

2.2 有限元模型分析精度

以第1.1節中介紹的兩種薄板試件的薄板－附加自由阻尼層復合結構為研究對象，并通過振動模態試驗結果驗證OSOS模型和OSH模型的建模精度。通過模態應變能法（MSE）得到兩試件分別在三種邊界條件下的模態頻率和模態損耗因子，見表2（有限元模型中試件的尺寸按其試驗時的工作面積確定）。可見：（1）由于試驗固支條件與仿真分析模擬固支條件的差異，試驗測量值基本小于仿真值。（2）OSOS模型和OSH模型都有較高的分析精度，但也有各自的特點。OSOS模型具有很高的計算效率和分析精度，但是對某些特殊的邊界條件不能客觀地進行模擬。如四邊固支（FSGZ）中，要求固支基板的邊界，而阻尼層的邊界不附加外部約束，OSOS模型中難以準確模擬這種邊界條件。試驗中試件周邊不附阻尼材料，仿真分析中同樣模擬該邊界條件，所以OSOS模型能夠較準確地模擬該邊界條件，仿真分析結果的精度較高。（3）相對于OSOS模型，OSH模型的計算效率較低（阻尼層為3層實體單元時，其計算時間是OSOS模型的5倍左右），但是其分析精度及適應性好于OSOS模型。

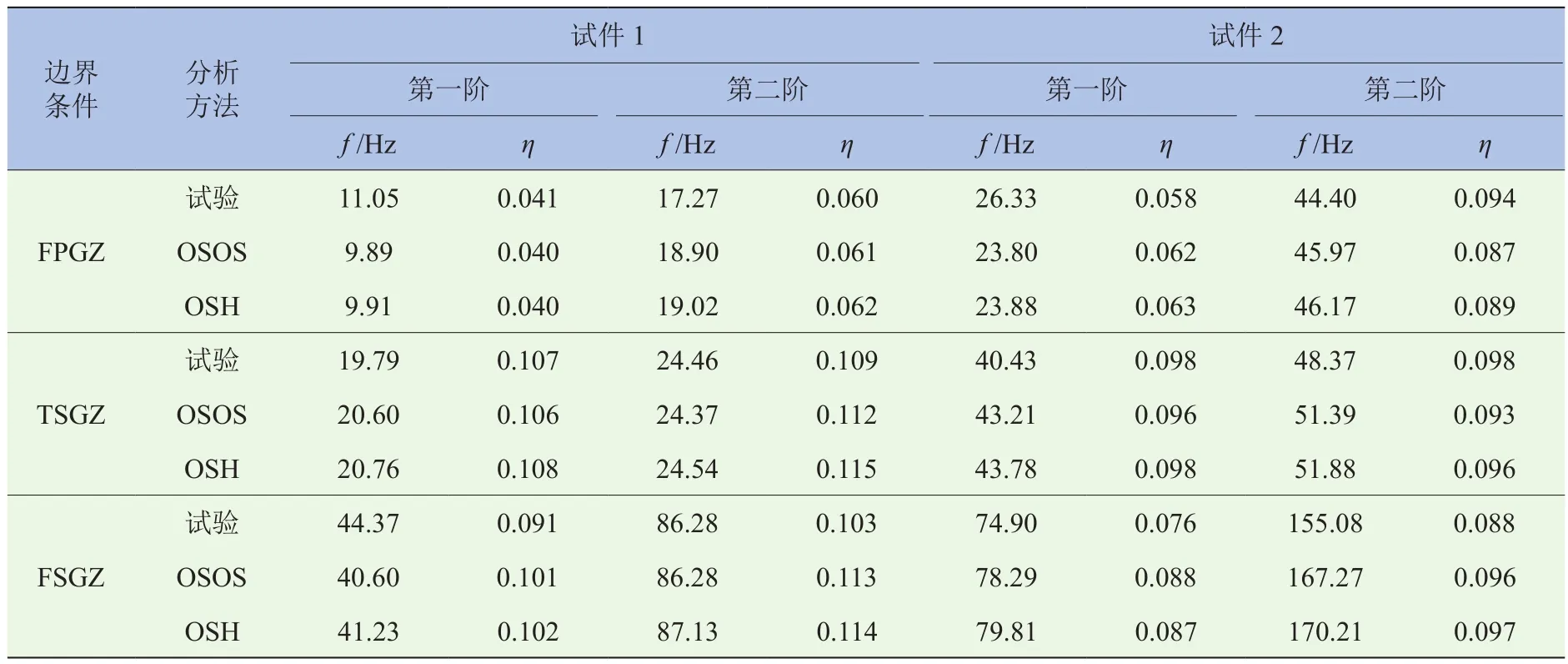
表2 附加自由阻尼層復合結構兩種建模方法的精度分析

3 薄板-附加阻尼層復合結構有限元建模與分析技術的進一步探討

3.1 薄板-附加約束阻尼層結構有限元建模技術

薄板－附加約束阻尼層結構也有多種有限元建模方法，圖7列出了三種常見的約束阻尼結構模型，為方便描述，分別簡稱為OSHOS[9]，SRHRS[10]，OSBOS[11-12]。OSHOS模型中，薄壁構件和約束層都采用偏置板殼單元構建模型。由于約束阻尼主要靠阻尼層的剪切變形來耗散能量，因此選用六面體實體單元對其進行建模，基板和約束層與阻尼層的接觸面通過變形協調關系使這兩個接觸表面的變形一致，該模型能夠反映結構的真實情況，具有較高精度。

SRHRS的基礎結構和約束層都采用普通的殼單元建模，粘彈性阻尼層實體單元的上、下表面的兩層節點分別與基礎層和約束層的殼單元的對應節點通過剛性單元連接，該模型不能準確描述基礎層上表面和約束層下表面與阻尼材料表面變形的協調關系。

OSBOS模型采用梁單元來模擬阻尼層，構建一種簡單的等效阻尼層模型。梁單元的幾何尺寸和材料參數根據殼單元尺寸的大小和阻尼材料的力學特性進行估算，如采用NASTRAN提供的CWELD焊點模型建立這種簡化的等效阻尼層模型。該模型與實際約束阻尼結構的差異較大，有明顯的缺點。其一，通過一維的梁單元模擬阻尼層結構，不能全面描述阻尼層的變形模式；其二，各梁單元之間的變形關系難以協調；其三，該方法要求研究人員有很強的工程經驗，只有這樣才能較準確地確定梁單元的參數。

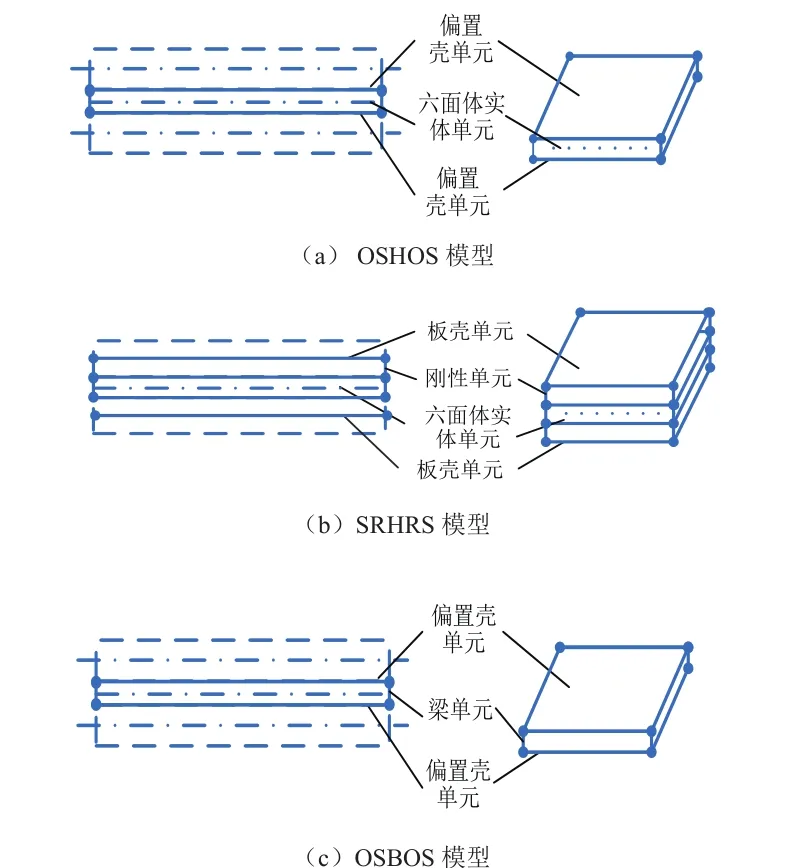
圖7 附加約束阻尼層復合結構的三種有限元建模方法

呂毅寧[8]利用OSHOS模型對某一簡支的薄板－附加約束阻尼層復合結構進行了建模，并分析其固有振動特性，將分析結果與解析結果進行對比后得出：OSHOS建模方法具有較高的建模精度，且模態應變能法同樣適用于約束阻尼層復合結構的設計與分析中；阻尼層實體單元的層數（≥3層）對模型精度的影響較小。

3.2 薄板-附加阻尼層復合結構的動態特性有限元分析方法研究

3.2.1 動態特性有限元分析方法比較

薄板－附加阻尼層復合結構的動態特性有限元分析方法主要包括復特征值法、MSE法及頻率響應分析法[13]。這里以第1.1節介紹的四點固支邊界條件下的試件1為分析對象，分別采用復剛度法、頻率響應法及模態應變能法計算其前2階的模態頻率及損耗因子，三種方法的計算效率對比（同樣的硬件條件）見表3。可見，模態應變能法具有最高的計算效率和較高的計算精度；直接頻率響應法的計算效率最低，該方法一般多用于計算附加薄板－結構阻尼復合結構的強迫振動響應，當模型規模很大或者激勵頻率點較多時，可采用計算效率更高的模態頻率響應法，但這種基于實模態的模態疊加法的理論體系還不完善，在某些特殊情況下（如模態密集的情形）需要注意分析結果的準確性，也可采用復模態疊加的方法來解決此類問題。

表3 三種分析方法的計算效率對比

3.2.2 模態應變能法分析薄板－附加阻尼層復合結構動態特性的精度

前述分析已表明薄板－附加阻尼層復合結構動態特性的三種分析方法中模態應變能法具有最高的分析效率，且有很高的分析精度，因此該方法得到了廣泛的應用。但是，針對模態應變能分析方法的適應性（何種結構特性下具有較高的分析精度）的研究還較少，下面將以一種典型的約束阻尼懸臂梁結構為研究對象，通過理論分析對MSE法的適應性進行初步探討。

DITARANTO[14]以縱向位移為設計變量推導了約束阻尼梁結構的動力學方程，RAO[15]運用分析力學的方法建立了約束阻尼梁結構的動力學方程。兩篇文章中阻尼材料的剪切應變只考慮了因約束層和基礎層的橫向位移產生剪切應變，從而引起的阻尼層的剪切應變，沒有考慮基礎層和約束層橫截面的轉動對其產生的影響，且沒有詳細介紹約束阻尼梁結構動力學方程的求解方法。MEAD等[16]以橫向位移為設計變量詳細介紹了約束阻尼梁結構的動力學方程，但是對動力學方程的求解方法沒有介紹。本文以約束阻尼梁結構的橫向位移為設計變量，分析得到了約束阻尼復合梁結構的通用動力學方程，如式（1）所示，該方程對應的特征方程如式（2）所示。并同時將其固支-固支、自由-自由等常見邊界條件以通用的表達式進行了描述，如本例中用到的自由-自由復合梁結構的邊界條件如式（3）所示。然后提出了一種單個參數的約束阻尼復合梁結構六階偏微分動力學方程的求解方法，由于篇幅限制這里不再詳細介紹這方面的工作，只將其應用于對MSE法適應性的討論中。

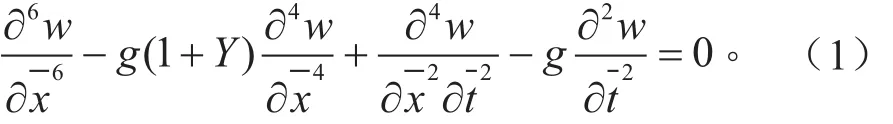
式中：w為撓度；Y為彎曲模量比；g為剪切模量比；

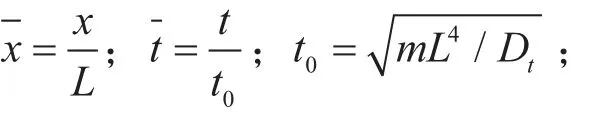
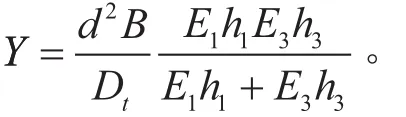
式（1）的解可寫成w =Aekxeiωt，則該動力學方程的特征方程為：

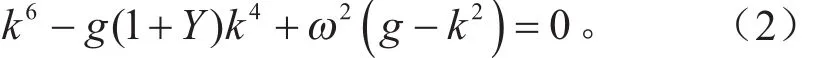
自由－自由復合梁結構自由端邊界條件的數學表達為：

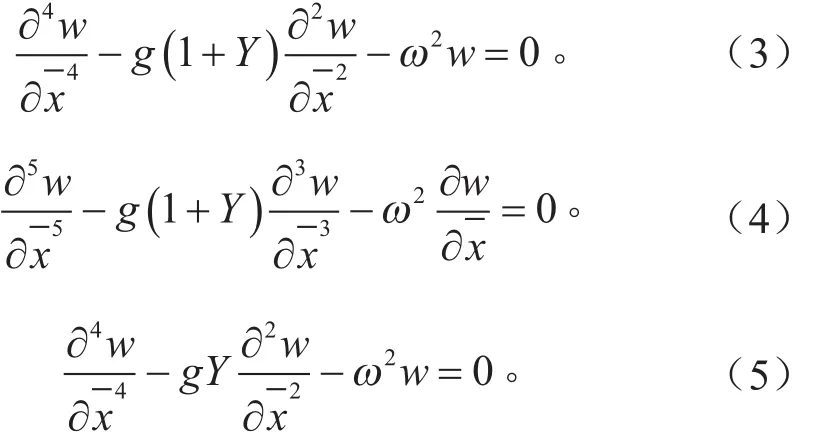
如式（2）～（5）所示的自由－自由約束阻尼懸臂梁結構的解析解形式不能顯示表達梁結構的固有振動頻率f和模態損耗因子ηv，因此采用數值分析的方法對式（2）～（5）進行求解，得到懸臂梁結構的振動特性，這種分析方法在下文中稱為半解析法。

以圖8所示的附加約束阻尼層復合梁結構（t1=1.0 mm，t2=0.3 mm，t3=0.5 mm，阻尼材料的剪切模量=0.896 MPa）為研究對象。假設阻尼層采用損耗因子為0.1的小阻尼材料，利用MSE法分析其在自由-自由邊界條件下該結構的振動特性，分析得到梁結構前四階彎曲振動的損耗因子和固有頻率，如圖9所示，并將其分析結果與解析解作對比分析。可以看出，采用MSE法對結構振動特性進行分析具有很高的精度，MSE法求得的結構固有頻率與解析結果基本一致；相對而言，MSE法分析得到的第一階彎曲振動的損耗因子的精度稍低。

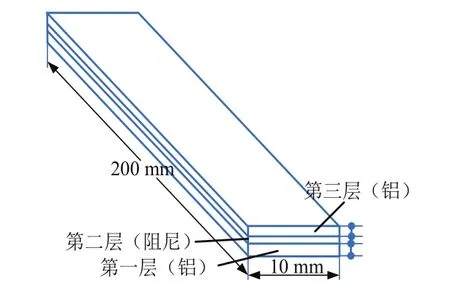
圖8 約束阻尼層結構示意圖

通過模態應變能法的定義式（6）可知，如果阻尼材料的力學參數中只有損耗因子變化，而其它參數都不變，采用該方法對結構進行振動特性分析時，其結構的損耗因子與阻尼材料損耗因子之比為一常數。為了詳細分析阻尼材料的損耗因子對結構損耗因子的影響，對該常數關系進行驗證，從而進一步確定MSE法的適應性。利用附加約束阻尼層復合梁結構的理論，分析了如圖8所示的附加約束阻尼層復合梁結構的振動特性。當采用了不同損耗因子的阻尼材料后，該薄壁梁結構的模態損耗因子與阻尼材料損耗因子的比值變化規律如圖10所示，可以得出以下結論：當阻尼材料的損耗因子小于0.8左右時，模態應變能分析方法具有很高的精度，但當材料具有很高的損耗因子時（大于1.0），模態應變能法的分析精度較低；隨著阻尼材料損耗因子的增加，約束阻尼復合結構的最大模態損耗因子在較小的剪切參數下即出現，也說明阻尼材料的損耗因子和剪切模量有一個最優的組合關系；當剪切參數較小時，如本例中g' ＜ 10 (G '＜2MPa)時，約束阻尼梁結構的損耗因子與材料損耗因子成正比，即該范圍內MSE法有較高的分析精度。

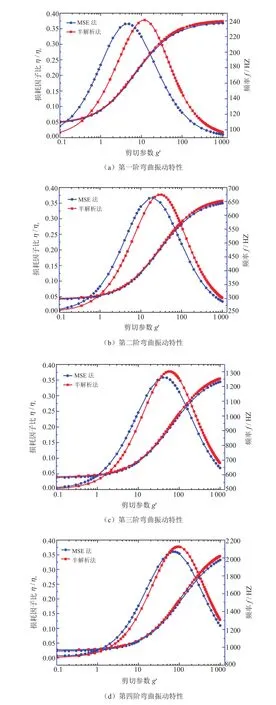
圖9 自由－自由約束阻尼梁前四階彎曲振動特性與剪切參數g'的關系

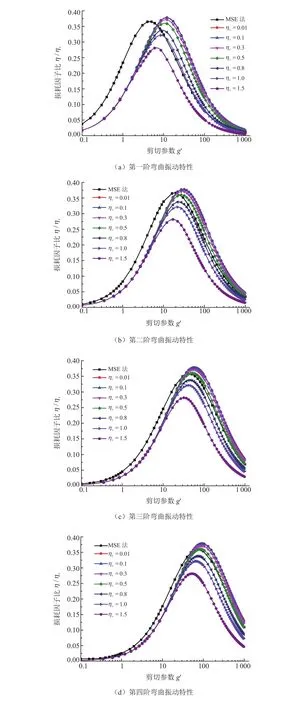
圖10 自由－自由約束阻尼梁模態損耗因子與材料損耗因子的關系

4 結論

（1）通過試驗分析了兩種規格的薄板－附加自由阻尼層復合結構在四點固支、兩邊固支和四邊固支的三種邊界條件下的固有振動特性，在此基礎上，研究了附加自由阻尼層復合結構有限元模型建模技術，并通過試驗驗證了所建立的有限元模型的精度。在薄板-附加自由阻尼層復合結構建模技術的基礎上，進一步探討了薄板-附加約束阻尼層復合結構的有限元模型建模技術。

（2）分析了薄板-附加阻尼層復合結構動態特性的三種有限元分析方法的精度及適用分析工況，并通過理論分析的方法對得到廣泛應用的MSE法的適應性進行了研究。分析認為當阻尼材料的損耗因子較小時（小于0.8），MSE法具有很高的分析精度，但當材料的損耗因子較大時（大于1.0），MSE法的分析精度則較低。

參考文獻（References）：

[1]龐劍，諶剛，何華. 汽車噪聲與振動——理論與應用[M].北京：北京理工大學出版社，2006.PANG Jian，CHEN Gang，HE Hua. Automotive Noise and Vibration—Principle and Application [M]. Beijing：Beijing Institute of Technology Press，2006.(in Chinese)

[2]ROY N，GERMèS S，LEFBVRE B，et al. Damping Allocation in Automotive Structures Using Reduced Models[C]//International Seminar on Modal Analysis(ISMA)，France，2006.

[3]SUBRAMANIAN S，SURAMPUDI R，THOMASON K R，et al. Optimization of Damping Treatment for Structure Borne Noise Reduction[C]//SAE Technical Papers，2003-01-1592，2003.

[4]RAO M D. Recent Applications of Viscoelastic Damping for Noise Control in Automotive and Commercial Airplanes [J]. Journal of Sound and Vibration，2003，262：457-474.

[5]呂毅寧，呂振華，趙波，等. 附加自由阻尼結構系統的有限元分析和拓撲優化設計方法研究[J].計算力學學報，2012，19(2)：178-183.LYU Yining，LYU Zhenhua，ZHAO Bo，et al. A Finite Analysis and Topology Optimization Method for Structures with Free Damping[J].Chinese Journal of Computational Mechanics，2012，19(2)：178-183.(in Chinese)

[6]王超，呂振華，鐘劍鋒. 識別粘彈性材料力學參數的自由阻尼試件設計方法研究[J].應用力學學報，2016，33(4)：582-588.WANG Chao，LYU Zhenhua，ZHONG Jianfeng. Research on Design Methods of Free Damping Specimens Used in Measurement of Viscoelastic Material’s Mechanical Parameters[J].Chinese Journal of Applied Mechanics，2016，33(4)：582-588.(in Chinese)

[7]王超，呂振華，顧葉青. 識別粘彈性阻尼材料力學參數用約束阻尼試件設計方法[J].中國機械工程，2016，27(9)：1208-1214.WANG Chao，LYU Zhenhua，GU Yeqing. Design Methods of Sandwich Specimen Used in Measurement of Viscoelastic Damping Material’s Mechanical Parameters[J].Chinese Journal of Mechanical Engineering，2016，27(9)：1208-1214. (in Chinese)

[8]呂毅寧.車身結構剛度和振動特性設計分析的幾個關鍵問題研究[D]. 北京：清華大學，2008.LYU Yining. Researches on Several Key Problems of Design and Analysis of Automotive Body Stiffness and Vibration Characteristics[D]. Beijing：Tsinghua University，2008. (in Chinese)

[9]SUN C T，LU Y P. Vibration Damping of Structural Elements[M]. New Jersey：Prentice Hall，1995.

[10]ETIENNE B，SYLVAIN G. Tools for Viscoelastic DampingTreatment Design：Application to an Automotive Floor Panel[C]//International Seminar on Modal Analysis(ISMA)，Leuven，2002.

[11]LU Y P，CLEMENS J C，ROSCOE A J. Vibrations of Composite Plate Structures Consisting of a Constrained-layer Damping Sandwich with Viscoelastic Core[J]. Journal of Sound and Vibration，1992，158(3)：552-558.

[12]KILLIAN J W，LU Y P. A Finite Element Modeling Approximation for Damping Material Used in Constrained Damped Structures[J]. Journal of Sound and Vibration，1984，97(2)：352-354.

[13]MSC Software Corporation. MSC Nastran Version 70 Advanced Dynamic Analysis User’s Guide[Z]. 2004.

[14]DITARANTO R A. Theory of Vibratory Bending for Elastic and Viscoelastic Layered Finite-length Beams[J].Journal of Applied Mechanics，1965，32(4)：881-886.

[15]RAO D K. Frequency and Loss Factors of Sandwich Beams Under Various Boundary Conditions[J]. Journal of Mechanical Engineering Science，1978，20 (5)：271-282.

[16]MEAD D J，MARKUS S. The Forced Vibration of a Three-layer，Damped Sandwich Beam with Arbitrary Boundary Conditions[J].Journal of Sound and Vibration，1969，10(2)：163-175.