2017年理綜全國Ⅰ卷第21題評析與教學啟示

許冬保

(江西省九江市第一中學,江西 九江 332000)

1 原題再現(xiàn)

2017年全國理綜卷Ⅰ卷第21題原題如下.

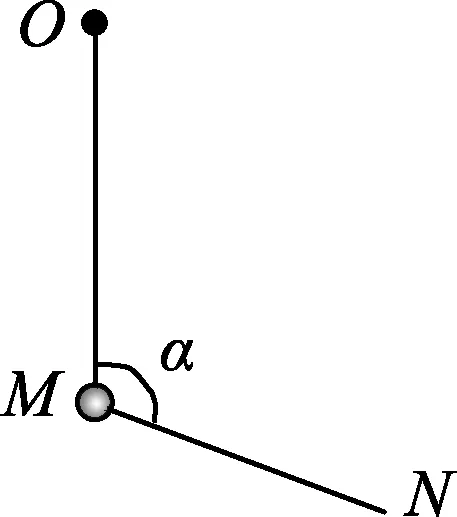
圖1

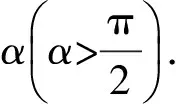
(A)MN上的張力逐漸增大.

(B)MN上的張力先增大后減小.

(C)OM上的張力逐漸增大.

(D)OM上的張力先增大后減小.

2 解答策略

在共點力平衡問題中,有一類通過控制某一物理量,使物體的狀態(tài)發(fā)生緩慢變化的動態(tài)平衡問題.該類問題涉及動態(tài)分析方法,要求在事物的動態(tài)變化中洞察、分析、推理,進而解決問題,這類問題的常規(guī)處理策略是解析法和圖解法.以下從不同的視角對試題予以分析.

2.1 解析法

解析法是對研究對象的某一狀態(tài)進行受力情況的分析,依據(jù)平衡條件,建立方程,求出因變量與

自變量之間的函數(shù)關系,然后根據(jù)自變量的變化規(guī)律確定因變量的變化情況.若物體僅受3個力作用,可尋找與力三角形相似的幾何三角形,建立比例關系,將力的大小變化問題轉化為幾何三角形邊長的變化問題進行討論.[1]

解法1:正交分解法.

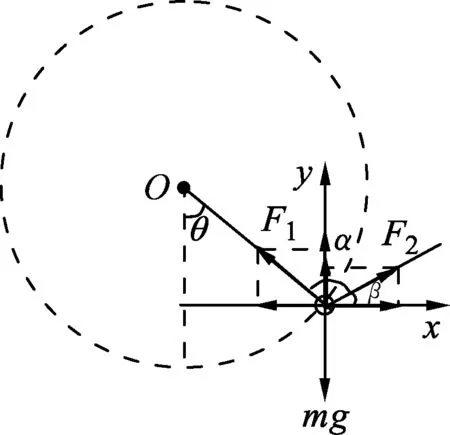
圖2

如圖2所示,在某一位置對重物進行受力分析,重物受到重力mg、繩OM的張力F1及繩MN的張力F2作用.建立平面直角坐標系,設繩OM與豎直方向的夾角為θ,F2與x正方向的夾角為β.由平衡條件,有

F2sinβ+F1cosθ-mg=0,F2cosβ-F1sinθ=0，

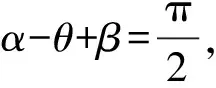
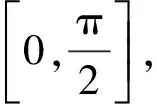
綜上,在整個變化過程中,力F1先增大后減小;力F2逐漸增大.選項(A)、(D)正確.

解法2:相似三角形法.

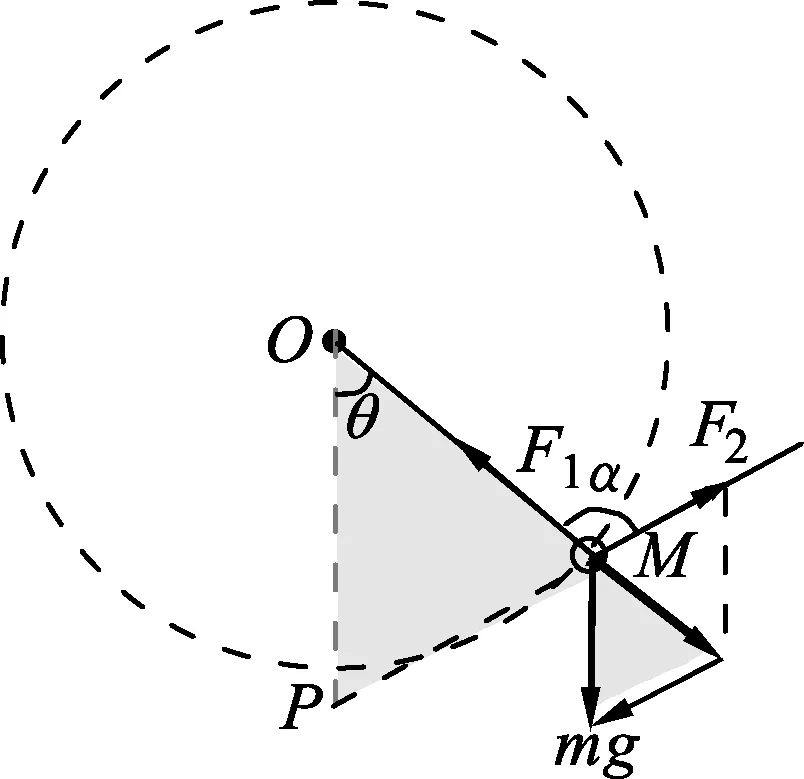
圖3

某一位置,繩OM與豎直方向的夾角為θ,受力情況如圖3所示,將力F2反向延長與過O點的豎直線相交于P點,由平衡條件知,重力mg與力F2合成所得合力與F1等值反向.考察圖3,圖中兩填充三角形相似,對應邊成比例.因此

于是可解得F1、F2.所得結果同上.

2.2 圖解法.

圖解法是根據(jù)平行四邊形定則或三角形定則畫出不同狀態(tài)下的力的矢量圖,然后由力矢量的變化判斷各力的變化情況.圖解法借助于矢量分析,能直觀地得到物理量之間的關系以及變化趨勢,從而極大地簡化分析及運算過程,提高思維的品質(zhì).[2]

解法3:圖解法

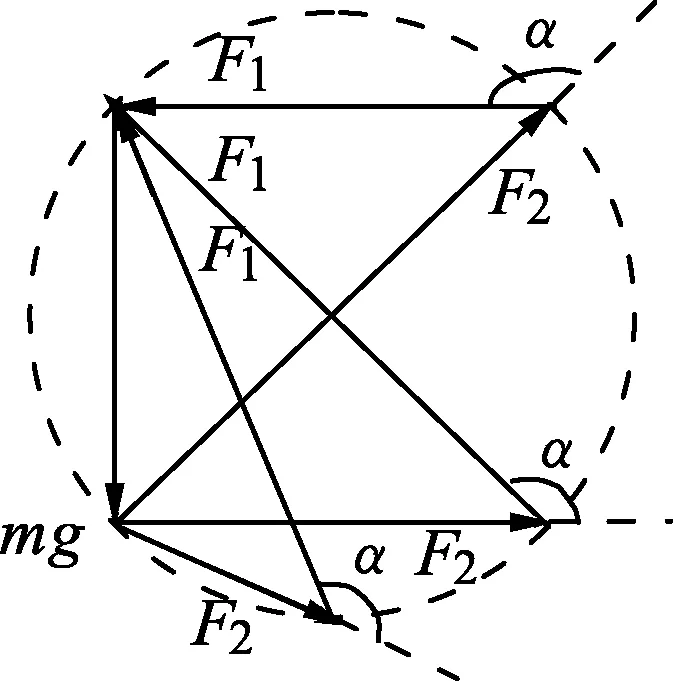
圖4

如圖4所示,設繩OM、MN的張力分別為F1、F2.在OM由豎直被拉到水平的過程中,重物緩慢拉起,重力mg及力F1、F2構成封閉矢量三角形.由于夾角α保持不變,因此,由幾何知識可知,矢量F1之箭尾或矢量F2之箭頭在以重力矢量大小為弦的同一圓周上滑動.以動態(tài)的視角考察圖4,可直觀得到,力F1先增大后減小(最大值對應圓的直徑);力F2逐漸增大(其最大值亦對應圓的直徑,但F2以此收尾).所得結果同上.

3 另類分析策略

一般物體的平衡,除了滿足共點力作用下的平衡條件之外,還有一個條件是滿足力矩平衡條件.后者在全國高考(上海市除外)考試大綱中未作要求.力矩平衡條件,即物體所受外力對某一轉軸的合力矩為零.力矩平衡條件作為拓展性內(nèi)容,對參與物理競賽及自主招生考試的考生,是必須掌握的學習內(nèi)容.

3.1 定性分析

解法4:力矩平衡條件定性分析法.

若以O點為轉動軸,在重物緩慢移動過程中,合力矩為零.顯然重力的力矩(順時針)不斷增大,而F2之力矩(逆時針)也不斷增大,由于其力臂保持不變,故力F2逐漸增大.若選擇圖1中繩端點N為轉動軸,等效于繩OM逆時針轉動,顯然重力之力矩先增大后減小,而力F1之力臂保持不變.因此,力F1大小先增大后減小.所得結果同上.

3.2 定量分析

解法5:力矩平衡條件定量分析法.

重物在某一位置時,同樣設繩OM與豎直方向的夾角為θ,參考圖3,由力矩平衡條件,有

mg·OM·sinθ=F2·OM·sinα.

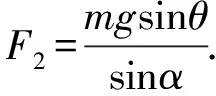
若以繩端點N為轉動軸,等效于繩OM逆時針轉動.同理,有

mg·MN·sin(π-α+θ)=F1·MN·sinα，

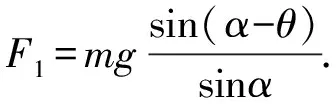
4 立意分析

物體的平衡是力學體系的基礎和核心知識,相互作用觀念下的動態(tài)平衡及其應用中的模型構建與分析推理,體現(xiàn)了高考突出對物理觀念、科學思維等核心素養(yǎng)的考查.

共點力的平衡在考綱中屬于Ⅱ類要求(與課標中的“理解”和“應用”相當).關于共點力平衡的考查,近年來高考試題主要的考查方式可劃分為3類:第1類是考查受力分析、力的合成與分解的方法,根據(jù)平衡條件定性分析(如2016年桌面上的物塊通過細繩跨過定滑輪及另一懸吊物塊約束下的平衡問題)或通過平衡條件建立方程求解問題(如2012年拖把平衡問題);第2類是對動態(tài)平衡問題的考查,在以往的考查中,受3力作用下的平衡系統(tǒng),其中,一個力的大小與方向不變,還有另一個力的方向不變,這是最經(jīng)典的動平衡問題(如2012年考查木板與墻面間夾一小球,木板轉動中小球的動態(tài)平衡問題);第3類是突出基礎性與綜合性的考查,表現(xiàn)為應用共點力的平衡條件解決彈簧系統(tǒng)的平衡問題(如2015年懸掛在彈簧下的通電導體棒在磁場中的平衡問題)、電磁感應現(xiàn)象中通電導體棒的平衡問題(如2016年斜面上的雙棒問題)等.

2017年考查的是一個力的大小及方向不變,另兩個分力方向均變化的動態(tài)平衡問題,試題構思巧妙,突破常規(guī),要求考生靈活運用所學知識分析解決動態(tài)平衡的問題.當考生發(fā)現(xiàn)所給問題不符合既定動態(tài)平衡的模型時,需要考生具備提出創(chuàng)造性見解的能力和品質(zhì).因此,試題考查了考生的理解能力與推理能力.在物理觀念及科學思維方面,有效地考查了相關的最高水平層級.

5 教學啟示

物理核心素養(yǎng)的考查要求考生能夠在不同情境下綜合利用所學知識和技能處理復雜任務,具有扎實的物理觀念和寬闊的物理視野,并體現(xiàn)出自身的實踐能力、創(chuàng)新精神等內(nèi)化的綜合學科素養(yǎng).核心素養(yǎng)下的關鍵能力的考查重點是,考查考生所學知識的運用能力,強調(diào)獨立思考、分析問題和解決問題.2017年動態(tài)平衡問題的考查帶給教學的啟示主要有以下3個方面.

(1) 授人以魚,不如授人以漁.如上所述,求解平衡問題的方法通常有,解析法及圖解法.解析法中又有正交分解法、合成與分解法及相似三角法等.對于動態(tài)平衡問題的處理,一般劃分為兩類,即圖解法及相似三角形法,而且這兩種方法適用于不同的情境.在教學中,方法的應用及掌握,單憑考生通過自己的訓練去掌握有關方法,效率較低.需要教師的隱性滲透與顯化教學,才能領悟、促進方法的掌握,進而內(nèi)化為自覺的學習行為.

(2) 跳出題海,重視科學思維.題海戰(zhàn)術,事倍功半.教學中應重視科學思維的訓練.科學思維作為對客觀事物本質(zhì)屬性、內(nèi)在規(guī)律和相互關系的認識方式,具有高度的抽象性和概括性,在教學中,要能夠幫助考生正確運用科學思維方法,能從定性(或半定量)和定量2個方面進行科學推理,找出規(guī)律并形成結論[3].

(3) 講究策略,提高思維品質(zhì).認知心理學家根據(jù)解決問題的效率將解題策略分為強方法和弱方法.對解決問題來說,效率較高的方法,屬強方法.效率較低的方法,則屬弱方法.物體只受3個共點力作用而處于動平衡狀態(tài),如果一個力矢量不變,另外還有一個力的方向不變,圖解法是強方法,解析法是弱方法;如果一個力矢量不變,另兩個力均在變,相似三角形法是強方法,矢量圖解法是弱方法.以上對試題的不同解法涉及不同的思維方法,不同的思維方法能反映思維品質(zhì)的優(yōu)劣.

總之,物理核心素養(yǎng)作為物理教學的重要目標,應當將物理觀念、科學思維、科學探究及科學態(tài)度與責任等核心素養(yǎng)的培養(yǎng)真正落實于教學活動中.

1 楊榕楠.更高更妙的物理·高考高分與自主招生決勝篇[M].杭州:浙江大學出版社,2013.

2 江四喜.物理競賽解題方法漫談[M].合肥:中國科學技術大學出版社,2014.

3 教育部基礎教育課程教材專家工作委員會,普通高中課程標準修訂組.普通高中物理課程標準 (征求意見稿)[R].北京,2016.