深度學習的模型搭建及過擬合問題的研究

陶礫+楊朔+楊威

摘 要： 深度學習是機器學習研究中的一個新的領域，它模仿人腦的機制來解釋數據，例如圖像，聲音和文本。文章介紹了一種多層感知器結構的深度學習神經網絡模型，并推導了其實現的算法。用數字識別實驗驗證了該模型及其算法的可靠性；驗證了過擬合的發生與訓練集的大小以及神經網絡的復雜度之間的重要關系。過擬合問題的研究對降低誤差有重要的意義。

關鍵詞： 深度學習； 神經網絡； 隱藏層； 過擬合

中圖分類號：TP391.9 文獻標志碼：A 文章編號：1006-8228（2018）02-14-04

Abstract： Deep learning is a new field in machine learning research. It simulates the mechanism of human brain to interpret data， such as image， voice and text. In this paper， a deep learning neural network model of multilayer perceptron structure is introduced and its implementation algorithm is derived. The reliability of the model and its algorithm are also verified by some digital recognition experiments， and find that the size of the training set and the complexity of neural networks are highly related with the over-fitting. It is of great significance to study the problem of over-fitting to reduce the error.

Key words： deep learning； neural networks； hidden layer； over-fitting

0 引言

深度學習的概念源于人工神經網絡的研究[3]。含多隱層的多層感知器就是一種深度學習結構。深度學習通過組合低層特征形成更加抽象的高層來表示屬性類別或特征，以發現數據的分布式特征表示。在深度學習泛化（generalization）過程中，主要存在兩個挑戰：欠擬合和過擬合（overfitting）。欠擬合是指模型不能在訓練集上獲得足夠小的誤差，而過擬合是指訓練誤差和測試誤差之間的差距太大。

1 模型設計

1.1 多層感知器結構[1]

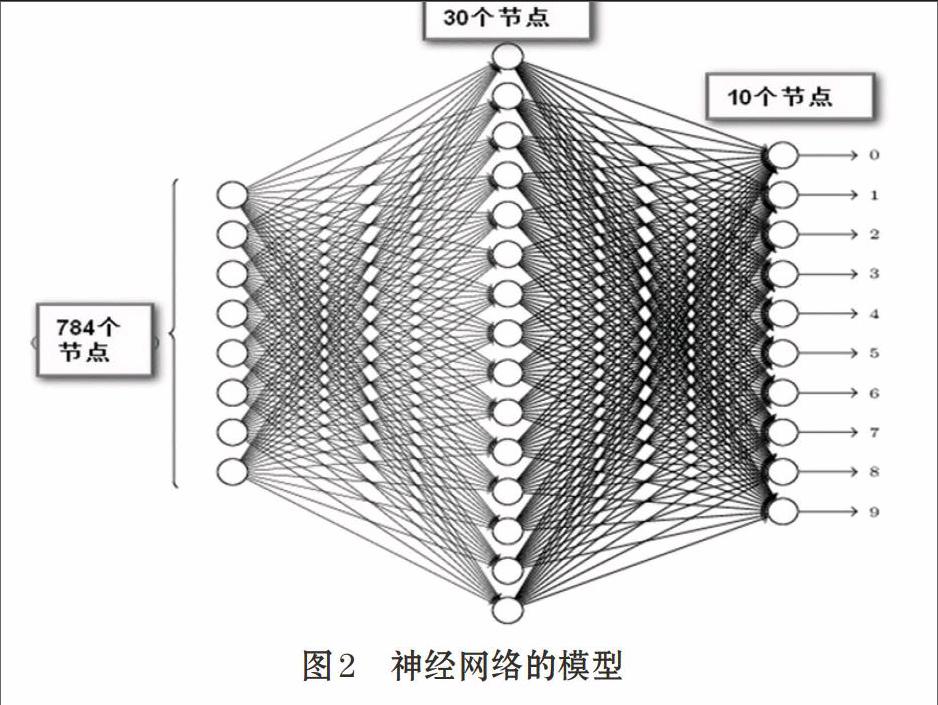
本文采用多層感知器（MLP）作為訓練模型，它是一種前饋人工神經網絡模型。它包括至少一個隱藏層（除了一個輸入層和一個輸出層以外）本文采用的多層感知器模型中的信號流傳播如下：

⑴ 輸入：yi（n）為i神經元的輸出，為下一個神經元j的輸入。

⑵ 誘導局部區域：神經元j被它左邊的yi（n）神經元產生的一組函數信號所饋，神經元j產生誘導局部區域。

⑶ 激活函數：神經元j輸出處的函數信號yi（n）為，其中為j層神經元的激活函數。采用激活函數的一個好處是引入非線性因素，使神經網絡變成非線性系統。本文采用Sigmoid函數作為激活函數，其定義為：，導數可用自身表示：

⑷ 誤差：k為輸出神經元，則誤差ek（n）=dk（n）-yk（n），其中dk（n）為信號輸出。

1.2 代價函數

代價函數是用來反映/度量預測結果yk（n）與實際結果dk（n）的偏差，本文采用最小平方（LMS）算法來構造代價函數：

1.3 隨機梯度下降算法[4]

本文采用隨機梯度下降算法（SGD）進行迭代，在此算法中，對的連續調整是在最速的方向進行的，即它是與梯度向量方向相反的。記為，因此，梯度下降算法一般表示為：。其中這里η是一個常數，稱為學習率參數，是梯度向量值。

1.4 反向傳播算法[5]

本文采用的反向傳播算法以與1.3節類似的方式對突觸權值應用一個修正值，它正比于偏導數，即：

1.4.1 神經元j是輸出節點

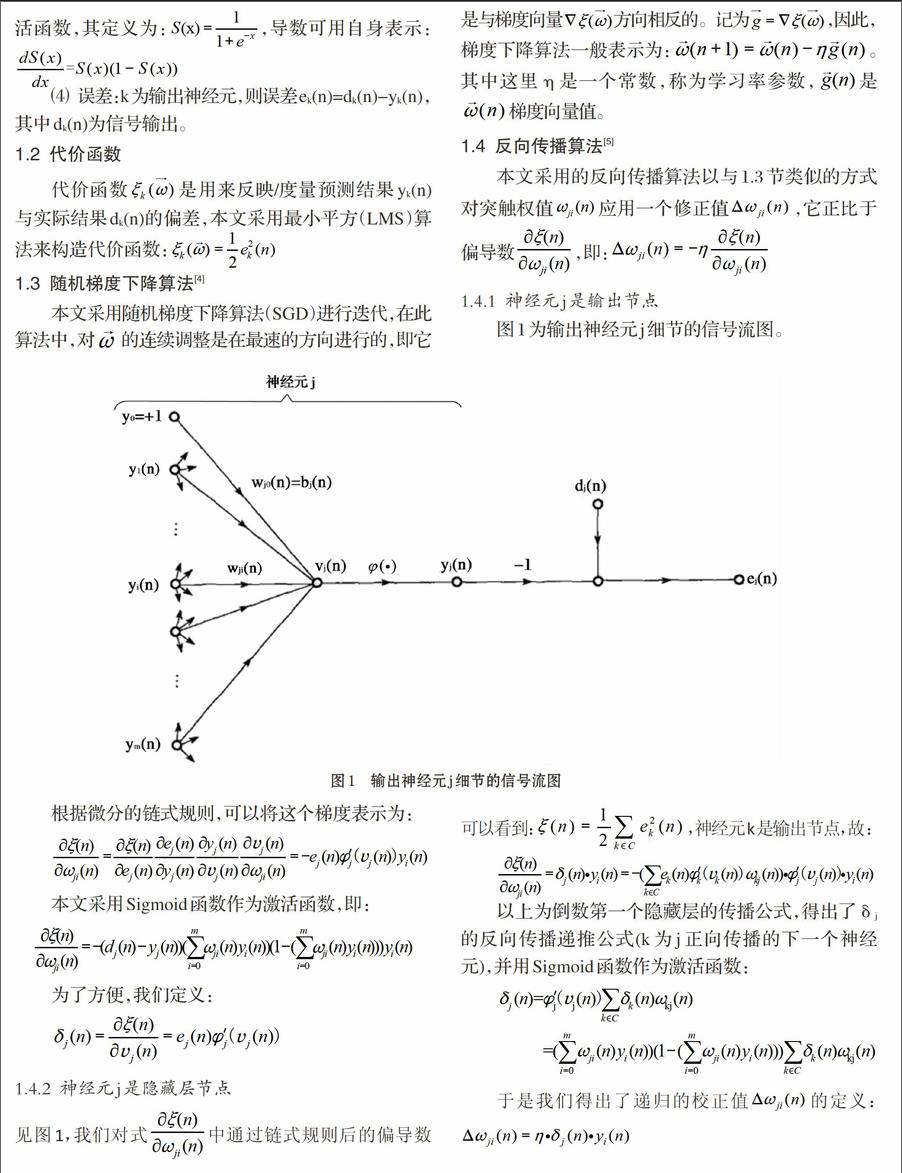
圖1為輸出神經元j細節的信號流圖。

根據微分的鏈式規則，可以將這個梯度表示為：

本文采用Sigmoid函數作為激活函數，即：

為了方便，我們定義：

1.4.2 神經元j是隱藏層節點

見圖1，我們對式中通過鏈式規則后的偏導數可以看到：，神經元k是輸出節點，故：

以上為倒數第一個隱藏層的傳播公式，得出了δj的反向傳播遞推公式（k為j正向傳播的下一個神經元），并用Sigmoid函數作為激活函數：

于是我們得出了遞歸的校正值的定義：

2 實驗

本模型以識別手寫數字為例，測試深度學習模型。本文采用的數據集為著名的“MNIST數據集”。這個數據集有60000個訓練樣本和10000個測試用例。我們首先對該模型進行驗證，然后通過調整訓練集的大小和神經網絡的結構來觀察其對正確率的影響。

2.1 模型算法

學習階段：本文采用mini-batch 梯度下降算法：假設總樣本數為Sn，將Sn隨機按每組N個樣本分為（Sn/N）組。多層感知器的突觸權值的調整在訓練樣本集合的所有N個樣本例都出現后進行。（Sn/N）次完成整個樣本集的訓練，構成了一個訓練的回合（epoch）。學習需經過多個回合，不斷完善。具體步驟如下。endprint