一種用于時空體元編解碼存儲的低計算量優化方法*

顧清華，馬 龍，盧才武

(西安建筑科技大學管理學院，陜西西安710055)

1 引言

近年來，地理信息系統受大數據環境的深入影響，時間變化的信息存儲管理備受關注［1］。時態地理信息系統TGIS(Temporal Geography Information System)組織的重點是時空數據庫STDB(Spatio-Temporal Data Base)［2］。時空體元作為 TGIS 中實體對象表達的最小單元，可動態反映地理空間內的事物，這就需要存儲海量的時間和空間屬性的數據，且這些數據需能在有限的存儲空間和傳輸速率下實現存儲轉換和表示計算。如何降低這些海量數據的存儲計算量則成為了解決這些問題的關鍵。目前，為了減少時空數據存儲空間，降低數據傳輸計算量，時空數據索引結構、數據編碼和存儲方法的優劣直接影響著STDB和TGIS的整體性能，它是解決二者之間數據存儲轉換、編解碼過程計算量的關鍵技術。

十六叉樹HDT(HexaDecimal Tree)索引結構最早是由Inamoto［3］在1993年提出的，經過不斷的實踐應用，該方法成為TGIS數據索引的關鍵技術［4］，實踐證明其對海量時空數據索引、查詢具有突出的特點，因此利用四維十六叉樹索引結構建立時空數據索引在需求上是完全合理的。但是，在十六叉樹索引結構中仍是采用十進制對時空對象進行編碼，這既無法滿足計算機存儲管理要求，又增加了時空數據存儲、轉換和傳輸過程的計算量。為此，Lacan 等與 Plank［5，6］采用傳統的范德蒙碼和柯西碼，構建了伽羅華有限域上的時空數據存儲系統和編碼方法。但是，在實際應用中，這兩種方法在編解碼轉換時存儲開銷大，兼容性差，并需借助查詢乘法表來完成域內體元乘法運算。Wardlaw與Plank 等［7，8］采用二進制矩陣表示域內體元，構建了二進制矩陣上的編碼方法，從而使存儲的體元數據編解碼過程具有更低的計算優勢。但是，如何進一步降低時空體元對象編解碼過程中的計算量，學術界只進行了簡單的探索，并未形成完整的解決方案。李德仁等［9］針對地理空間體元計算的復雜性問題，采用一種新的網格分裂方法，實現了空間對象網格編碼策略、存儲方法以及地球空間坐標的轉換方法。郭達志等［10］根據時態GIS的應用需求，構建了四維時空數據模型，解決了時空對象線性編碼、存儲計算和時空坐標轉換問題。但是，這些索引結構、編解碼和存儲方法均有各自的適用范圍，對于時變范圍較大或存在多個局部極小點的數據索引、存儲表示計算量還大。因此，本文根據地理空間實體動態變化特征，提出了一種用于時空網格體元模型編解碼存儲的低計算量優化方法，通過對網格體元對象的編碼表示和存儲轉換，構建了時空網格體元編解碼優化方法，使得網格體元模型在時空數據庫中存儲、表示、轉換和數據傳輸過程中的計算量進一步降低，并對時空網格體元編解碼的時空復雜度和優化算法進行分析。最后的實驗結果表明，本文提出的方法可有效降低編解碼存儲過程中約30%左右的計算量。

2 時空網格體元編碼及轉換方法

2．1 時空網格體元編碼和解碼模型

十六叉樹本質上是對目標網格體元的動態存儲方式，也是實現體元編解碼表示和數據索引的結構。由十六叉樹編碼圖解［10］可知，該索引結構對于空間體元對象標識與地理時空坐標位置上存在著嚴格的對應關系，可較好地實現地理時空對象編解碼的轉換與計算。時空網格體元對象的解碼數學模型為:

其中，ci、di、ei、fi(i=n －1，n －2，…，0) 的取值為0或1，分別為 X、Y、Z、T軸上坐標值所對應在網格體元中的解碼值權系數，p為網格體元分裂的次數或分辨率。

每個十六叉樹節點的編碼采取的形式為qn－1，qn－2，…，0。每個位置上的 qi是從(0，1，…，10，A，…，F)十六個數中取其中之一，qi的個數取決于上述分辨率p。時空網格體元對象的編碼數學模型為:

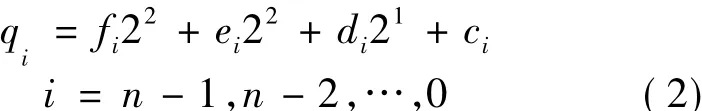
其中，qi為編碼值，ci、di、ei、fi分別為 X、Y、Z、T 軸上坐標值所對應網格體元的編碼數據權系數。

2．2 時空網格體元編碼存儲轉換

對地理時空網格體元對象編解碼后還需滿足系統存儲要求，即將用十進制表示的空間實體對象轉換為二進制形式。因此，本文借助高斯坐標的3DGIS編碼方法［11］，設計出符合地理網格體元對象編碼存儲轉換方法，其轉換步驟如下:

Step 1定義時空區域參照基點O(x0，y0，z0，t0)。

Step 2定義固定時間t周期內沿著X、Y、Z軸的網格體分割尺寸 Dx、Dy、Dz，結合十六叉樹原理［10］，通常 Dx、Dy、Dz定義為2nm(n=1，…，10)，Dt定義為日期型數據。且根據研究區域內空間實體對象的變異頻度和復雜度來確定n:當變異頻度很高時，可選擇低值(n=0，1);當變異頻度適中時，可選擇中值(n=2，3);當變異頻度很低時，可選擇高值(n=4，5)，t選取為采樣數據的時刻。

Step 3按規定尺寸(Dx×Dy×Dz)和給定的時間點，把目標網格體元區域劃分為四維空盒集，如圖1所示;劃分后的目標區域內網格體編碼可以采用時空網格體元編碼模型(如式(2)所示)，如圖2所示。

Step 4計算任意地理空間實體對象A的二進制編碼:

(1)定義實體對象A的近基點A0:實體對象的最小包圍盒的最近角點為近基點A0(x，y，x)，其表達式為min［(x－x0)2+(y－y0)2+(z－z0)2］;當存在兩個以上的近基點時，任選其一。

(2)計算近基點A0空盒集區域的行號I(沿X軸)、列號J(沿Y軸)和層級號(沿Z軸)以及時間點編號，其計算表達式參考文獻［12］。

(3)將近基點A0所在空盒的十進制行列層次號(I，J，K)轉換為二進制行列層次號(I'，J'，K')。

(4)獲取二進制行列層次號(I'，J'，K')中每一位二進制數 Pit、Pjt、Pkt，及時間編號:

其中，＆ 為“與”操作符，t為位的序號，t=1，2，3，…，n。

(5)基于二進制行列層次號(I'，J'，K')計算時空實體對象A所在空盒的二進制Morton碼:

3 時空網格體元編解碼計算優化

3．1 二進制解碼矩陣構建

根據Wardlaw有限域空間體元方法［6］，如果采用B0表示有限域網格體元對應的二進制矩陣，則構建的二進制解碼矩陣的形式為:

其中，Bxk∈{B0，B1，B2，…，B2m－1}。

由矩陣的性質可知，對矩陣行列變換后，矩陣的秩不變，將R矩陣轉化為如下的形式:

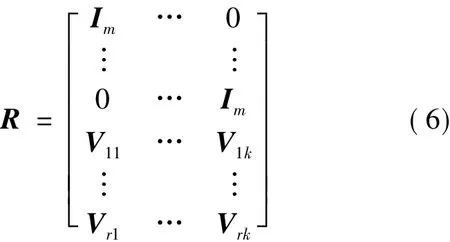
其中，Im為m×m的單位矩陣;I為(m×k)×(m×k)的單位矩陣;Vij為由0、1構成的m×m方陣;V'是(m×r)×(m×k)的0、1矩陣。

因為 Vi1，…，Vik是一個由 0、1構成的 m ×(m ×k)矩陣，［Vi1，…，Vik］是由 1×(m ×k)階的0、1構成的行向量，由此可將十進制表示的體元對象編解碼換算為二進制形式，從而實現網格體元數據塊的校驗和容錯。

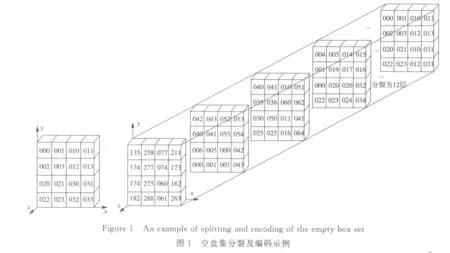
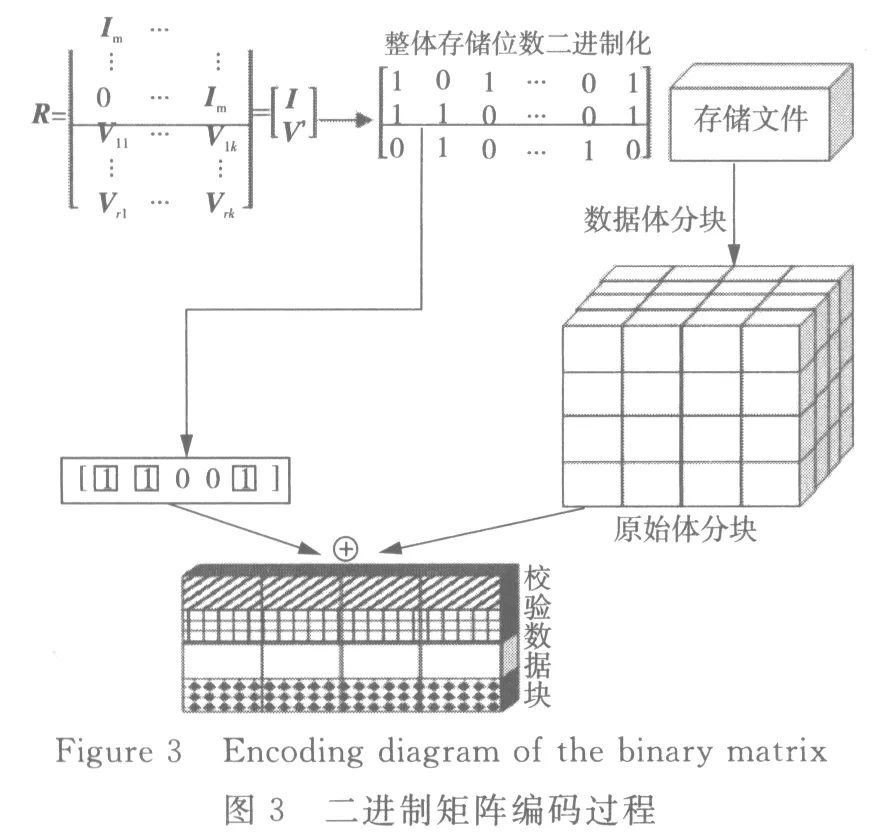
在二進制碼存儲的過程中，檢驗網格體元數據塊將行向量中體元1對應的所有網格體元數據塊之間進行異或運算，進而獲取校驗的網格體元數據塊(圖2中陰影劃分塊部分)。具體計算過程如圖3所示。

3．2 時空網格體元編碼與解碼過程的低計算量優化算法

在實際的應用過程中，借助二進制編碼矩陣的存儲方法，采用異或運算實現編解碼的校驗和容錯，降低整個網格體元編解碼存儲的計算量。其總體優化思路:首先通過Wardlaw的方法構造有限域體元的二進制編碼矩陣;然后根據網格體元校驗塊最優次序算法，依次計算出二進制編碼矩陣中各向量間的關系;最后依據校驗塊優化計算方法，先計算出由向量本身確定的校驗塊異或計算次數，再從已知向量的校驗塊間接搜索計算出其余向量的未知校驗塊。通過減少向量間的校驗塊計算的異或次數，從而降低整個網格體元編碼存儲過程中的計算量。反向計算過程，即是解碼過程的優化方法。

設任意網格體元編碼矩陣形式如式(7)所示:

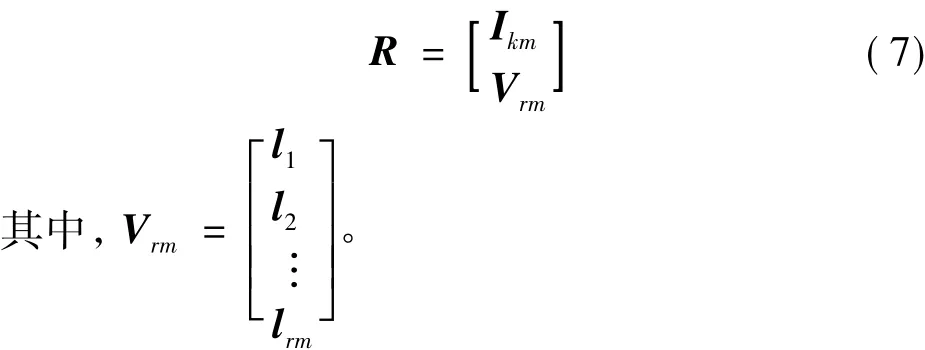
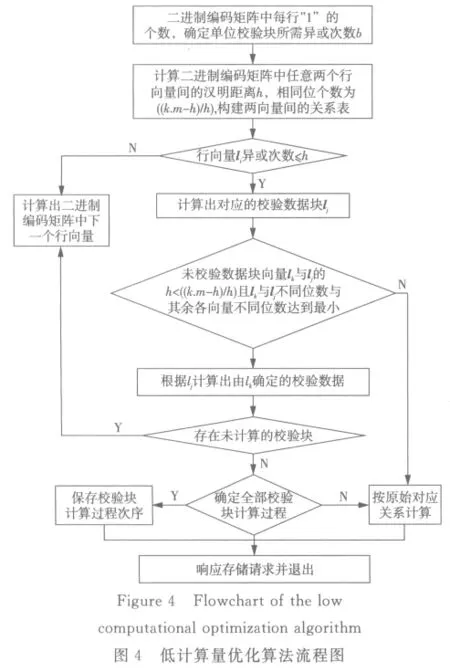
則可根據生成的校驗塊Vrm中的行向量l1，l2，…，lrm為“1”的數量確定出異或計算次數。其優化算法的流程如圖4所示。

4 工程應用與結果分析

4．1 數據來源

為了驗證本文所提出的時空體元對象編解碼、存儲過程計算量算法的有效性，使用SURPAC礦業軟件對某礦山的經緯度坐標和礦床高程數據進行處理后，獲得該礦山某采場的礦體空間塊體數據模型，時間屬性以采剝與否的實際時間為基準，并對復雜礦體模型數據進行簡化處理，選取礦床中部分塊體的地理時空坐標數據集(X，Y，Z，T)={(6，3，4，1)，(0，2，3，1)，(2，1，0，0)，(2，0，2，0)}作為典型實驗數據，采用SURPAC軟件處理的體元數據模型如圖5所示。

4．2 時空網格體元數據編解碼

由2．1節介紹的時空網格體元對象編解碼的數學模型可知，選取空間分辨率n=3，時間點t=0時，表示不開采，其空間坐標(X，Y，Z)分別為(2，1，0)、(2，0，2);時間點 t=1 時，表示開采，其空間坐標(X，Y，Z)分別為(6，3，4)、(0，2，3)。將這兩組數據集代入模型(2)中可獲得四組不同的編碼值(或定位碼);反之，根據給定的解碼值與網格體元數據權系數，將對應的編碼值代入模型(1)中，可計算出對應的解碼值。詳細計算結果如表1與圖2有灰色填充標識的體元所示。

Table 1 Encoding and decoding of spatiotemporal grid voxel data表1 時空網格體元數據編解碼表

4．3 數據編碼存儲轉換方法

根據2．2節可知，網格體元編解碼是十進制表示形式，需要將其轉換為二進制形式，并需確定目標網格體元的高斯坐標的基點和近基點。本文選取時間點 t=1，解碼值為(X，Y，Z)=(6，3，4)所在的目標區域為例，其對應的基點值為O(5 433 903．01，2 073 356．22，－200．0)，實體對象 A 的近基點為 A0(543 721．73，2 073 464．85，－332．1)。定義Dx=Dy=26m=64 m，Dz=24m=16 m。則其對應的 I、J、K 及 MT 碼如下:

其中，函數INT()表示向上取值。

4．4 時空網格體元編解碼低計算量優化算法

4．4．1 網格體元解碼

由3．2 節可知，依然以時間點 t=1，(X，Y，Z)=(6，3，4)為例，選取構造有限域元素參數m=3，根據 Plank等人［13］提出的二進制矩陣構造方法，隨機選取3個二進制矩陣B1、B2、B5，則構造的二進制矩陣如式(8)、式(9)所示:

矩陣R優化后:

其中，I為9×9的單位矩陣，V'如式(11)所示;

根據空間坐標(6，3，4)的二進制解碼矩陣R中的子矩陣 V'，可確定向量 l1，l2，l3，…，l9，依據優化算法需確定出編碼矩陣中各向量間的關系，如表2所示。其中，la(b)中a表示矩陣V'的行向量順序，b表示第a行向量生成校驗塊時的異或計算次數，((k×m－h)/h)中k×m－h為矩陣V'中任意兩個向量間的相同體元位的個數，h為矩陣V'中任意兩個向量間的漢明距離;(x/y)表示任意兩個行向量li與li+1間相同體元個數x與不同體元個數y。

以上述解碼矩陣V'中第1、2行向量l1和l2為例，在表2中標記為l1(3)與l2(4)，直接由l1和l2計算網格體元的校驗塊的異或次數分別為3和4，而向量所需校驗塊異或次數均小于由其它校驗塊間接計算的異或次數，即l3生成的校驗塊為p1，3可直接計算獲得;同理l1、l7、l8的校驗塊由對應的行向量直接經異或運算獲得，即直接獲得的校驗數據塊分別為:

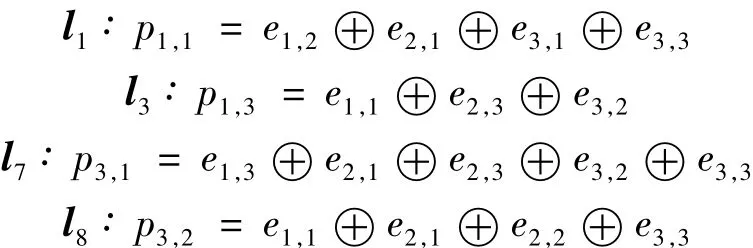
通過已計算獲得的網格體元校驗塊l1、l3、l7、l8可計算出其余向量對應的體元校驗塊數據。從表2可知，從l1至其它行向量的漢明距離知，可由l1的校驗塊來計算出l9的體校驗數據塊，可由l8的校驗塊計算出l4的校驗塊，由于從l3、l6的校驗數據塊來確定l9的校驗數據塊需要更少的異或次數，因此，l1無法作為校驗其余行向量的基礎校驗數據塊。同理，l3、l7也無法作為基礎校驗數據塊。依次搜索，由圖6可知，分別通過l4的3次校驗數據塊異或次數計算出l5的校驗數據塊，l6的校驗數據塊可分別計算出l2、l9的校驗數據塊，即間接獲得的校驗數據塊分別為:

Table 2 Relationship of decoding vectors of spatiotemporal grid voxel data表2 時空網格體元數據解碼向量關系

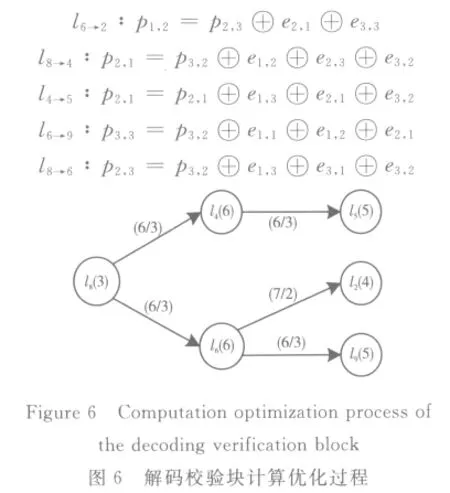
至此解碼矩陣所生成的所有校驗數據塊計算結束，其整體計算流程如圖7所示。由此可知，將地理空間對象分裂為網格體元時，對其中的有形實體對象解碼所產生的存儲計算量較少，而對于地形中的“空”位置解碼就會造成大量的存儲計算。

4．4．2 網格體元編碼

對于時空網格體元數據解碼過程而言，當存儲的體元數據丟失或毀壞時，可通過校驗矩陣K來恢復。因為基于矩陣K的解碼過程同樣需要通過完整的備份數據塊間的異或計算來恢復丟失數據，從線性分組碼的性質知，解碼與編碼存在著嚴格的對應轉換關系。因此，可直接將網格體元解碼矩陣與編碼矩陣進行轉換，設編碼矩陣如式(12)所示，則校驗矩陣如式(13)所示:

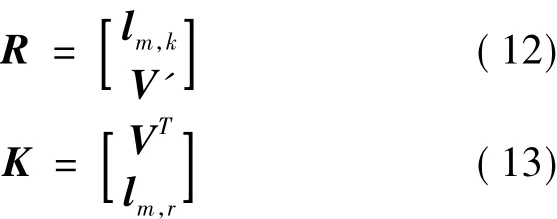
矩陣K可用來恢復丟失的體數據塊，設存儲體數據塊B1，B2，…，Br的節點丟失，則隨機選擇k個節點備份的網格體元編碼數據塊對丟失數據進行恢復。根據校驗矩陣K(k+r)×r恢復丟失掉的r個數據塊 B1，B2，…，Br，依據上述提出的校驗塊優化計算方法將丟失的網格體元數據塊B1，B2，…，Br分別表示為X1，X2，…，Xr，并根據上述網格體元數據校驗塊最優次序算法，將恢復過程中需要完整備份的編碼數據塊記為 Br+1，Br+2，…，Bk，Bk+1，…，Bk+r+1，Bk+r;令 φ = ［X1，X2，…，Xr，Dr+1，…，Dr+k］，其中 φ1=［X1，X2，…，Xr］;φ2=［Dr+1，…，Dr+k］。則根據關系式 φ．K(k+r)×r=0來恢復丟失的體數據塊。同樣，根據上述關系式中 φ與K(k+r)×r間的關系可以定位出丟失體數據塊在校驗矩陣K(k+r)×r中所對應的向量，如果丟失的體數據塊所對應的矩陣表示為K1r×r，校驗矩陣 K(k+r)×r中與完好備份的數據塊對應的矩陣表示為K2r×r，那么有:

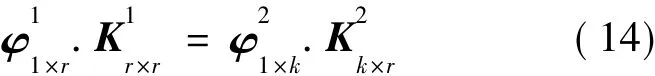
因為對于空間坐標系(6，3，4)中網格體元解碼的恢復特征可知，系統最多可允許3個數據塊丟失，上述提出的算法恢復過程中假設原始網格體元數據全部丟失，只有完整的備份數據塊時，才可說明丟失數據塊的數據恢復過程。其中，

則通過式(18)確定的校驗矩陣行向量間的關系，其中，l'1，…，l'9表示丟失數據塊的向量順序，分別如表3與圖8所示。

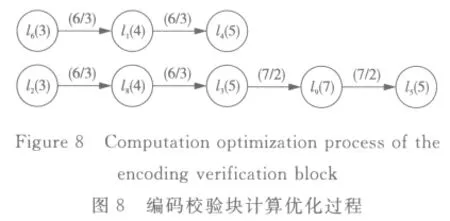
通過圖8可獲得丟失數據塊的最優計算次序，首先，計算由l1、l6、l7確定的丟失數據塊;其次，根據l2的數據塊，計算出由向量l8確定的丟失數據塊，同時根據l6數據塊，計算出l1數據塊;然后根據向量l8計算出l3數據塊，并根據向量l1計算出l4、l5的數據塊;最后根據恢復后的向量l3計算出l9確定的數據塊。其整體計算流程如圖9所示。

4．5 時空網格體元存儲過程的計算量分析

由于地理時空網格體元存儲形式可由二進制矩陣表示，因此測試的數據集分別用不同規模的二進制矩陣構成。測試平臺所用的硬件為Intel core i5-4590M，3．3 GHz CPU，軟件為 Matlab2015R，時空網格體元數據分別為64×64、128×128、256×256的二進制數值矩陣，十六叉樹的葉子節點數目分別為2 095、940、4 590、22 628 個，數值矩陣隨機生成。網格體元分裂時間和存儲效率如表4所示。

由圖2可知，假設將地理時空網格體從上至下劃分為三個子立方體區域，其中區域I為64×64，葉子節點數目分別為2 095個、940個，區域Ⅱ為128×128，葉子節點數目為4 590個、區域Ⅲ為256×256，葉子節點數目為22 628個。三個實驗區的時空網格體元編碼是從頂向下分裂方法產生十六叉樹，采用式(2)編碼，Morton編碼采用八叉樹的自頂向下分裂方法，可用式(4)編碼。

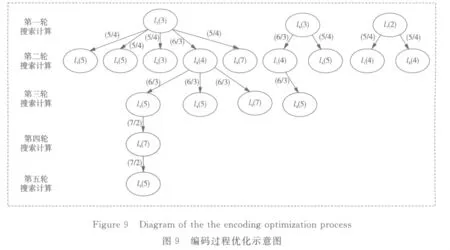
Table 3 Relationship of encoding vectors of spatiotemporal grid voxel data表3 時空網格體數據編碼向量關系

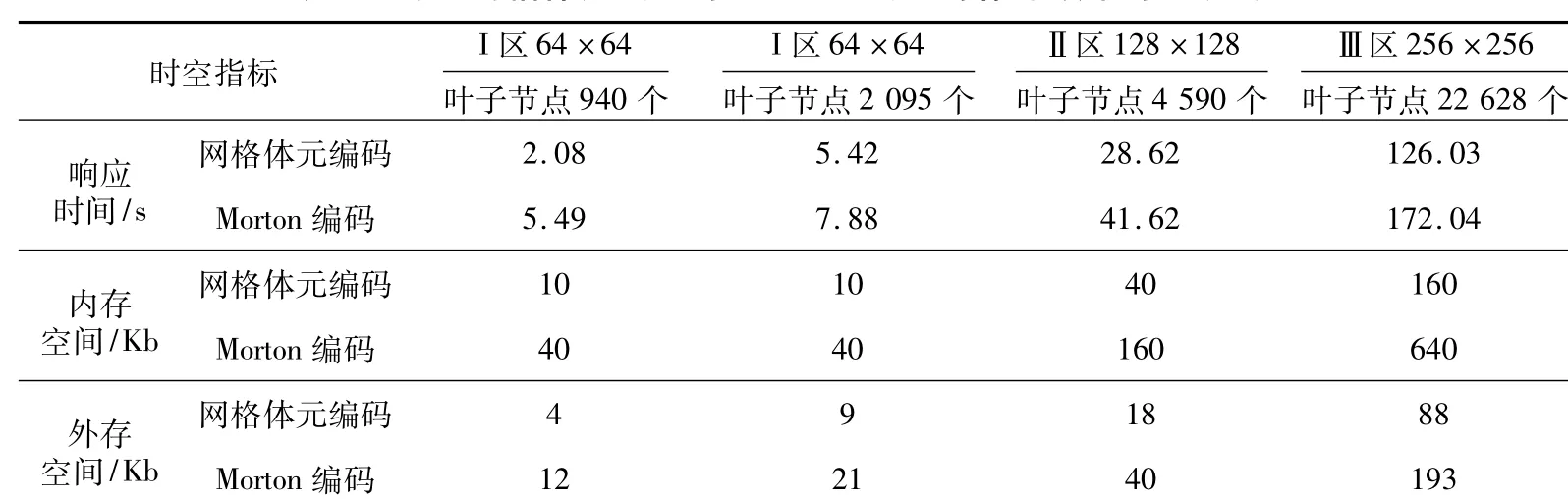
Table 4 Storage efficiency and splitting time of spatiotemporal grid voxel encoding and Morton encoding表4 時空網格體元編碼與Morton編碼的存儲效率與分裂時間

由表4的結果可知，分別采用以十六叉樹索引結構和八叉樹索引結構為基礎的兩種編碼方法，采用十六叉樹索引結構對地理空間目標塊體分裂所消耗的時間幾乎是采用八叉樹索引結構的一半左右，隨著礦床塊體數量和葉子節點數量的增加，以八叉樹索引結構的Morton編碼所消耗的分裂時間明顯增加。采用以十六叉樹索引結構的網格體元編碼所占用的內存空間要比采用八叉樹索引結構的Morton編碼少25%左右，隨著礦床塊體數量和葉子節點數量的增加，兩種編碼方法占用的內存空間成倍數增長。這是因為十六叉樹對目標空間塊體的索引是以子立方體的形式分裂，而且分裂過程中會隨著時間區域的變化而不斷地釋放已訪問節點的內存空間，而八叉樹索引結構只是在同一立方體上對目標空間塊體進行遞歸分裂，分裂過程中已訪問節點由于根節點的關聯性而無法釋放，由此導致十六叉樹索引方法占用的存儲空間較少，分裂速度較快。同理，兩種編碼方法占用的外存空間也是以倍數在增長，網格體元編碼方法所占用的外存空間要明顯少于Morton編碼方法占用的外存空間。

4．6 低計算量優化方法分析

為驗證提出的計算方法的通用性，分別對時間參數 t=1 與空間參數為(6，3，4)，(0，2，3)以及時間參數為 t=0，空間參數為(2，1，0)，(2，0，2)的時空網格體元的編碼與解碼過程進行了測試。上述編碼與解碼系統都由本文提出的方法構建，其低計算量優化性能如表5所示。

由表5可知，以構建的(6，3，4)編碼矩陣為例，如果用傳統的分塊計算，需計算38次方可獲得全部校驗塊，而使用本文方法只需要計算26次，總的運算次數減少31%左右。對于文中生成的9個校驗數據塊的編碼矩陣，每個校驗塊需要約2．9次異或運算，因此極大地減少了計算量，從而大幅度地降低了計算時間，節約了存儲空間，其優化后的編碼計算時間如圖10所示。

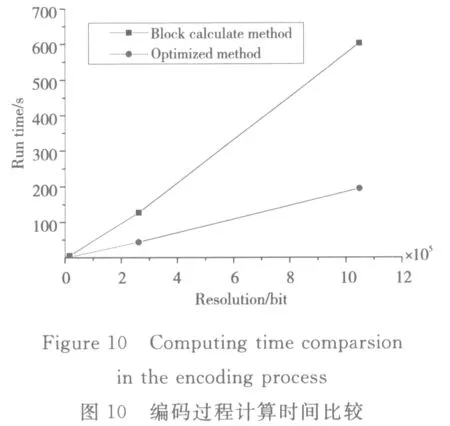
如果用傳統的塊計算方法進行解碼，需要38次異或運算恢復丟失的全部體數據塊，采用本文方法后，只需24次異或運算，即總的運算次數減少大約37%，因此極大地減少了恢復丟失數據的計算量，降低了時空復雜度。圖11所示為解碼過程計算時間的比較。同時，對表5中的二進制解碼過程進行了統計分析，由于缺失網格體編碼的數據塊不同，解碼過程也會有所差別。因此，將測試條件設置為所有原始塊體數據缺失，利用校驗數據塊對其進行恢復，使用本文方法后，解碼過程的計算量大約減少30%。

Table 5 Computation comparison between encoding optimization and decoding optimization表5 編碼與解碼優化計算量比較

5 結束語

在海量時空數據存儲和傳輸計算過程中，需要對動態產生的地理空間對象數據進行存儲，本文提出的優化計算方法可減少時空體元存儲過程中計算量的30%左右，系統響應時間減少約50%。同時，該方法具有一定的通用性，凡是涉及時空體元編解碼存儲和二進制矩陣確定的塊體異或運算過程，均可采用該方法降低系統存儲過程中的計算量。但是，該方法只是針對已經構建的二進制塊體矩陣的編解碼存儲過程進行優化，如何直接構造出最低計算量的編解碼矩陣還需進一步深入研究。