一種應(yīng)用于大角度變換點(diǎn)云的配準(zhǔn)方法

李 健，楊靜茹，何 斌

?

一種應(yīng)用于大角度變換點(diǎn)云的配準(zhǔn)方法

李 健1，楊靜茹1，何 斌2

(1. 陜西科技大學(xué)電氣與信息工程學(xué)院，陜西 西安 710021；2. 同濟(jì)大學(xué)電子與信息工程學(xué)院，上海 201804)

針對(duì)傳統(tǒng)配準(zhǔn)法不能很好解決大角度變換點(diǎn)云的配準(zhǔn)這一問(wèn)題，提出一種基于精確對(duì)應(yīng)特征點(diǎn)對(duì)及其鄰域點(diǎn)云的配準(zhǔn)方法。首先分別計(jì)算兩組點(diǎn)云的FPFH值，根據(jù)特征值建立點(diǎn)云間的對(duì)應(yīng)關(guān)系；然后通過(guò)RANSAC濾除其中錯(cuò)誤的匹配點(diǎn)對(duì)，得到相對(duì)精確的特征點(diǎn)對(duì)集合；之后通過(guò)KD-tree搜索的方式分別找出特征點(diǎn)對(duì)半徑鄰域內(nèi)的點(diǎn)，應(yīng)用ICP算法得到兩部分點(diǎn)云的最優(yōu)收斂；最后將計(jì)算得到的相對(duì)位置關(guān)系應(yīng)用到原始點(diǎn)云上得到配準(zhǔn)結(jié)果。通過(guò)對(duì)斯坦福大學(xué)點(diǎn)云庫(kù)中Dragon、Happy Buddha模型以及Kinect采集的石膏像數(shù)據(jù)進(jìn)行配準(zhǔn)和比較，實(shí)驗(yàn)表明該方法能夠有效解決大角度變換點(diǎn)云的配準(zhǔn)問(wèn)題，是一種具有高精度和高魯棒性的三維點(diǎn)云配準(zhǔn)方法。

點(diǎn)云配準(zhǔn)；快速點(diǎn)特征直方圖；隨機(jī)采樣一致；迭代最近點(diǎn)；KD-Tree

三維重建是計(jì)算機(jī)視覺(jué)中的一個(gè)重要組成部分，包含點(diǎn)云的采集、去噪、配準(zhǔn)、融合、紋理映射等步驟，點(diǎn)云配準(zhǔn)是三維重建中最重要也是最復(fù)雜的一步。現(xiàn)有的深度相機(jī)等三維測(cè)量設(shè)備一次只能測(cè)量物體一個(gè)方向上的數(shù)據(jù)，因此要得到物體的三維模型就必須將多次測(cè)量得到的點(diǎn)云數(shù)據(jù)通過(guò)配準(zhǔn)合并成一個(gè)完整的三維模型。

點(diǎn)云配準(zhǔn)這一概念自上世紀(jì)提出以來(lái)，涌現(xiàn)出了許多經(jīng)典的算法。BESL等[1-2]提出的迭代最近點(diǎn)(iterative closest point，ICP)算法原理簡(jiǎn)單且易于實(shí)現(xiàn)，但需要為待配準(zhǔn)點(diǎn)云提供一個(gè)較好的初值，否則迭代結(jié)果容易陷入局部最優(yōu)。在基于特征的配準(zhǔn)算法中，RUSU等[3]提出的點(diǎn)特征直方圖(point feature histograms，PFH)計(jì)算方式通過(guò)多維直方圖來(lái)描述查詢點(diǎn)與鄰域點(diǎn)之間的空間差異。PFH的改進(jìn)算法稱為快速點(diǎn)特征直方圖(fast point feature histograms，F(xiàn)PFH)[4-5]，F(xiàn)PFH在降低算法復(fù)雜度的同時(shí)保留了PFH大部分的特性，但該方法容易生成錯(cuò)誤的對(duì)應(yīng)關(guān)系從而導(dǎo)致配準(zhǔn)失敗。在基于幾何形狀的配準(zhǔn)算法中，4PCS算法[6-7]通過(guò)查找兩個(gè)點(diǎn)集上全等且共面的四邊形建立對(duì)應(yīng)關(guān)系，但對(duì)于重疊區(qū)域較小的點(diǎn)集，通常難以找到對(duì)應(yīng)關(guān)系。基于4PCS方法的Super4PCS算法[8]改善了這一問(wèn)題，但其時(shí)間復(fù)雜度仍然遠(yuǎn)高于同類算法。

上述算法對(duì)于簡(jiǎn)單的點(diǎn)云配準(zhǔn)問(wèn)題大都能得到較好的效果。但實(shí)際的應(yīng)用場(chǎng)景中，待配準(zhǔn)的點(diǎn)云往往存在重合區(qū)域過(guò)小、點(diǎn)云間變換角度大等情況，傳統(tǒng)算法在這樣的場(chǎng)景下往往難以得到理想的效果。本文提出一種基于精確對(duì)應(yīng)特征點(diǎn)對(duì)及其鄰域點(diǎn)云的配準(zhǔn)方法，融合FPFH、隨機(jī)采樣一致性(random sample consensus，RANSAC)算法[9]與ICP算法，基于PCL[10]實(shí)現(xiàn)，能夠較好地解決復(fù)雜場(chǎng)景下的點(diǎn)云配準(zhǔn)問(wèn)題。

1 算法總體描述

當(dāng)兩片點(diǎn)云的初始位置變換角度過(guò)大時(shí)，難以通過(guò)一次配準(zhǔn)就得到滿意的結(jié)果，因此通常需要先經(jīng)過(guò)粗配準(zhǔn)步驟對(duì)兩片點(diǎn)云進(jìn)行初始配準(zhǔn)，得到近似的旋轉(zhuǎn)平移矩陣。在粗配準(zhǔn)提供的良好初始匹配的基礎(chǔ)上，精配準(zhǔn)步驟通過(guò)進(jìn)一步的計(jì)算能夠得到兩幀點(diǎn)云間更為精確的相對(duì)位置關(guān)系。本文方法分為粗配準(zhǔn)和精配準(zhǔn)兩個(gè)步驟，具體流程如圖1所示。

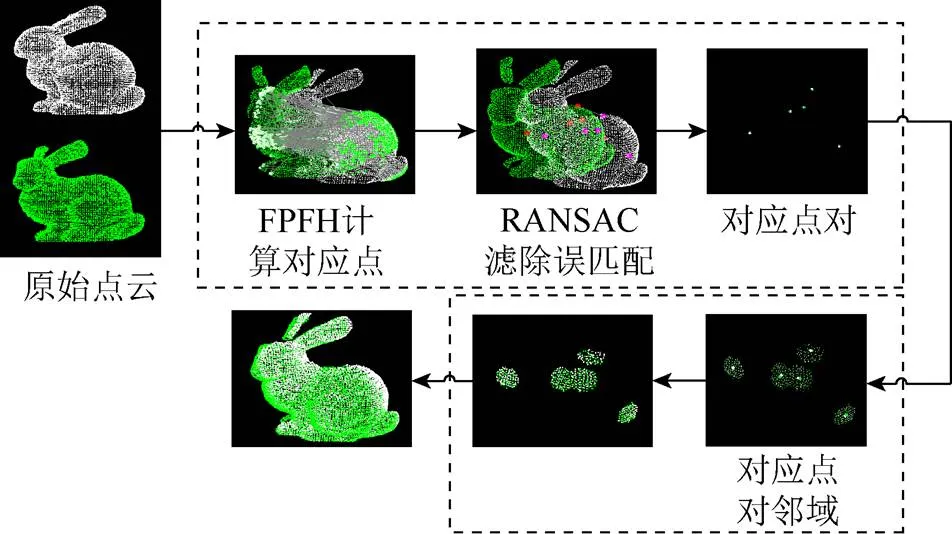
圖1 本文算法流程示意圖

圖1中的原始點(diǎn)云分別為源點(diǎn)云和參考點(diǎn)云。在粗配準(zhǔn)過(guò)程中，采用基于特征的FPFH方法得到初始對(duì)應(yīng)關(guān)系，再通過(guò)RANSAC算法濾除誤匹配，得到相對(duì)精確的對(duì)應(yīng)關(guān)系。在精配準(zhǔn)過(guò)程中，為減少計(jì)算量，采用KD-Tree搜索[11]的方式選取精確對(duì)應(yīng)點(diǎn)對(duì)的半徑鄰域點(diǎn)云，應(yīng)用ICP算法計(jì)算兩部分點(diǎn)云的位置關(guān)系，將該變換關(guān)系應(yīng)用到原始點(diǎn)云上得到最終的配準(zhǔn)結(jié)果。

2 算法詳細(xì)描述

2.1 基于FPFH的粗配準(zhǔn)

粗配準(zhǔn)采用基于快速點(diǎn)特征直方圖計(jì)算方式的方法來(lái)實(shí)現(xiàn)，具體的步驟包括特征計(jì)算、誤匹配篩除等步驟。

2.1.1 快速點(diǎn)特征直方圖描述子搜索對(duì)應(yīng)點(diǎn)

FPFH是一種空間局部點(diǎn)特征描述子，通過(guò)計(jì)算查詢點(diǎn)與其鄰域內(nèi)元素的法線之間的關(guān)系來(lái)表示點(diǎn)云表面的變化情況，并通過(guò)一個(gè)多維直方圖對(duì)點(diǎn)云的幾何特性進(jìn)行描述。FPFH計(jì)算的影響區(qū)域如圖2所示。

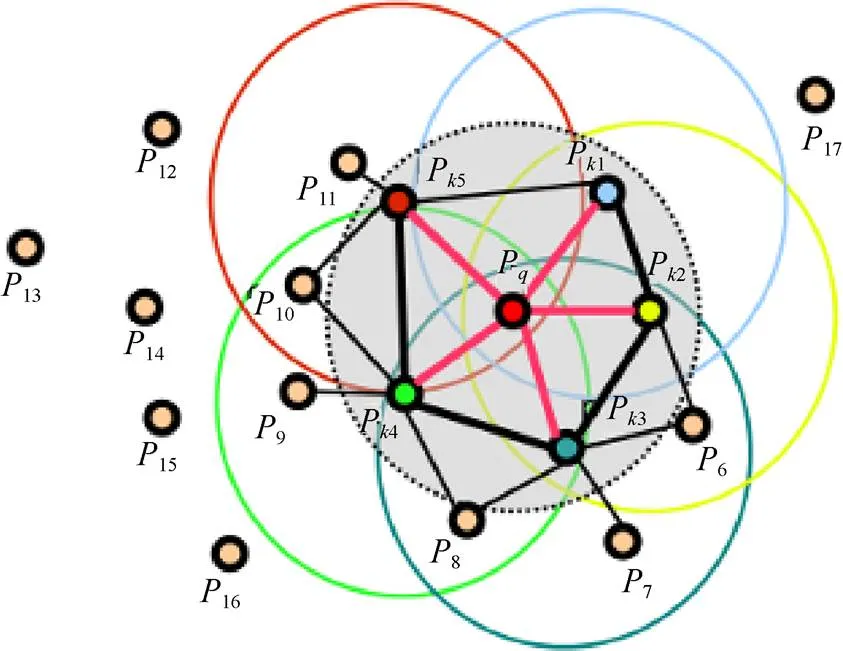
圖2 FPFH影響區(qū)域示意圖

查詢點(diǎn)P位于圖2中半徑為的球形中心，查詢點(diǎn)與其所有鄰元素相互連接。為方便計(jì)算兩點(diǎn)間的關(guān)系，在坐標(biāo)系中計(jì)算任意兩點(diǎn)P和P及與其對(duì)應(yīng)的法線n和n之間的相對(duì)偏差。坐標(biāo)系如圖3所示。

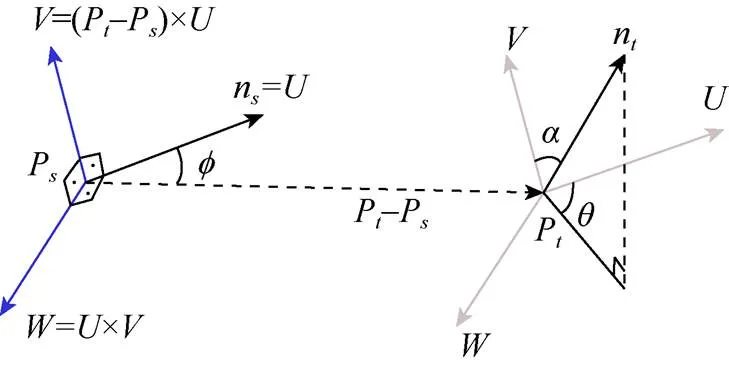
圖3 UVW坐標(biāo)示意圖

3個(gè)方向分別用、、表示，其中

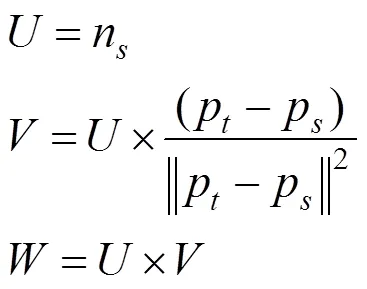
使用的坐標(biāo)系，法線n和n之間的差可以化解為下面3個(gè)角度的差異，即

分別將、、從0°~360°等分為11個(gè)區(qū)間，創(chuàng)建一個(gè)有33個(gè)等分區(qū)間的直方圖，每個(gè)區(qū)間對(duì)應(yīng)特定范圍內(nèi)特征值的個(gè)數(shù)。按照如下步驟計(jì)算查詢點(diǎn)的FPFH值：

步驟1.計(jì)算查詢點(diǎn)P與其影響區(qū)域內(nèi)所有點(diǎn)的3個(gè)特征值，統(tǒng)計(jì)每個(gè)區(qū)間所對(duì)應(yīng)的特征值的個(gè)數(shù)，得到簡(jiǎn)化的點(diǎn)特征直方圖SPFH。

步驟2.重新確定每個(gè)點(diǎn)的鄰域，根據(jù)式(3)使用鄰近的SPFH計(jì)算的最終FPFH。

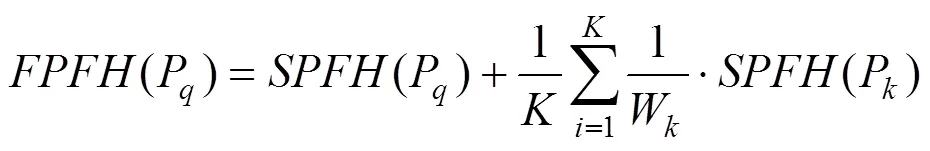
其中，P為P的鄰域點(diǎn)；權(quán)重W是P與P之間的距離；為鄰域點(diǎn)P的個(gè)數(shù)。

計(jì)算得到的快速點(diǎn)特征直方圖如圖4所示，圖4(b)為4(a)中某點(diǎn)的快速點(diǎn)特征直方圖。

2.1.2 RANSAC濾除誤匹配

通過(guò)比較FPFH值得到的對(duì)應(yīng)關(guān)系并不是完全正確的，采用RANSAC算法剔除其中的錯(cuò)誤匹配，能夠得到相對(duì)準(zhǔn)確的對(duì)應(yīng)關(guān)系。

RANSAC算法是一種簡(jiǎn)單有效的去除誤匹配的方法，通過(guò)建立一個(gè)特定的數(shù)學(xué)模型將數(shù)據(jù)點(diǎn)分為“內(nèi)點(diǎn)”和“外點(diǎn)”，采用迭代估計(jì)的方法計(jì)算出最優(yōu)參數(shù)模型，找到的不符合該模型“外點(diǎn)”為誤匹配點(diǎn)，符合模型的“內(nèi)點(diǎn)”為精確匹配。以圖5為例，圖中實(shí)線對(duì)應(yīng)正確匹配，線條兩點(diǎn)為“內(nèi)點(diǎn)”，虛線為誤匹配，線條端點(diǎn)為“外點(diǎn)”。

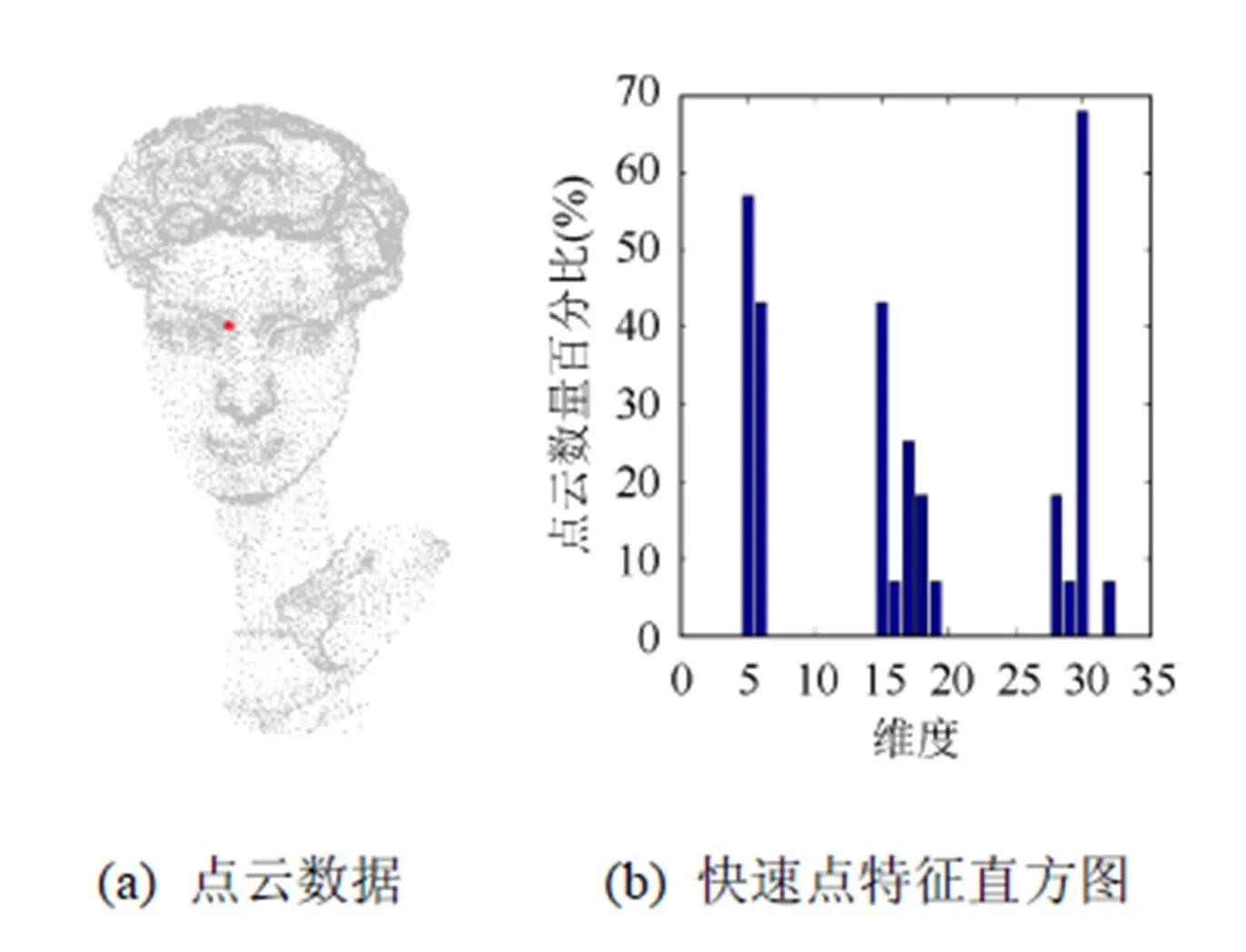
圖4 快速點(diǎn)特征直方圖示例

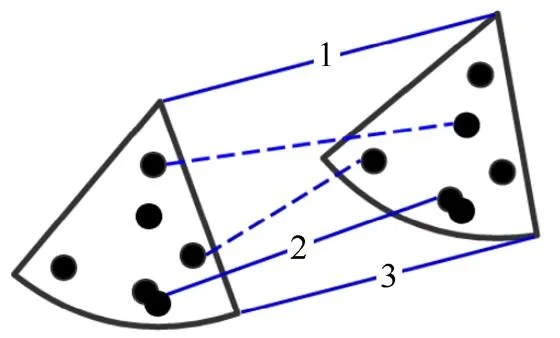
圖5 RANSAC示意圖

RANSAC步驟結(jié)束后可以得到較為正確的匹配關(guān)系。但由于FPFH計(jì)算方式描述的是查詢點(diǎn)與其鄰域點(diǎn)之間的關(guān)系，這一特性導(dǎo)致在點(diǎn)云表面曲率變化較小或者點(diǎn)云密集的區(qū)域中相鄰點(diǎn)的FPFH值非常接近，因此可能會(huì)發(fā)生對(duì)應(yīng)到正確匹配附近點(diǎn)的情況，如圖5中2號(hào)對(duì)應(yīng)關(guān)系所示，由于相鄰點(diǎn)的FPFH值非常接近，所以根據(jù)特征值判定圖5中2號(hào)線兩端的點(diǎn)為對(duì)應(yīng)點(diǎn)。該對(duì)應(yīng)關(guān)系雖不完全準(zhǔn)確，但卻在RANSAC步驟所建立數(shù)學(xué)模型的容差范圍內(nèi)，所以認(rèn)定其為正確匹配。這種不準(zhǔn)確的映射關(guān)系會(huì)對(duì)配準(zhǔn)結(jié)果產(chǎn)生負(fù)面影響，也是需要精配準(zhǔn)步驟的原因。

2.2 基于關(guān)鍵點(diǎn)鄰域的精配準(zhǔn)

在粗配準(zhǔn)所提供的初始匹配的基礎(chǔ)上，精配能夠進(jìn)一步改進(jìn)和完善配準(zhǔn)結(jié)果。精配準(zhǔn)分為基于KD-tree的關(guān)鍵點(diǎn)鄰域搜索和ICP計(jì)算變換關(guān)系兩個(gè)步驟。

2.2.1 基于KD-tree的關(guān)鍵點(diǎn)鄰域搜索

粗配準(zhǔn)步驟結(jié)束后，可以直接通過(guò)ICP算法計(jì)算點(diǎn)云的變換關(guān)系，但在已經(jīng)得到較為精確的對(duì)應(yīng)關(guān)系的前提下，通過(guò)KD-tree搜索的方式選擇對(duì)應(yīng)點(diǎn)鄰域計(jì)算相對(duì)位置關(guān)系，可以節(jié)省計(jì)算成本。使用KD-tree搜索的方式選擇對(duì)應(yīng)點(diǎn)對(duì)半徑內(nèi)的點(diǎn)云計(jì)算最終的變換關(guān)系矩陣。

在具體的搜索過(guò)程中，將特征點(diǎn)作為查詢點(diǎn)輸入，給定查詢點(diǎn)和查詢距離的閾值(即查詢半徑)，從點(diǎn)云找出所有與查詢點(diǎn)距離小于閾值的點(diǎn)。如圖6所示，以空間中一點(diǎn)P為圓心，給定的查詢距離為半徑畫球體，球體內(nèi)點(diǎn)與P的距離小于半徑的點(diǎn)即為所要查找的鄰域點(diǎn)。

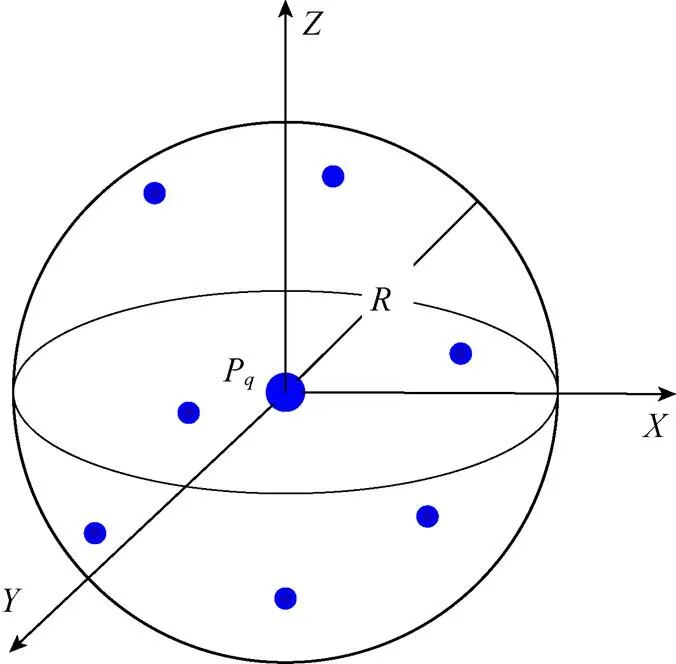
圖6半徑搜索示意圖

2.2.2 ICP計(jì)算變換關(guān)系

通過(guò)半徑搜索得到的對(duì)應(yīng)區(qū)域是整體模型的一部分，只計(jì)算該部分點(diǎn)云的變換關(guān)系能夠節(jié)約計(jì)算成本，將計(jì)算得到的、矩陣應(yīng)用到原始模型上即可得到最終配準(zhǔn)結(jié)果。

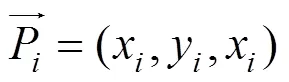
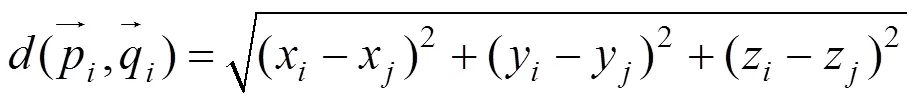
三維點(diǎn)云的配準(zhǔn)問(wèn)題可轉(zhuǎn)化為求解使式(5)中目標(biāo)函數(shù)最小時(shí)的和的問(wèn)題，即

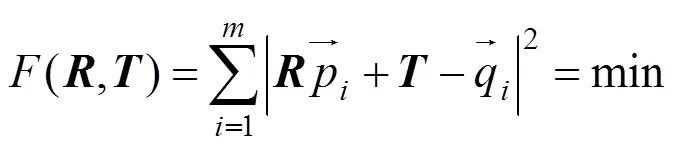
其中，為點(diǎn)集中對(duì)應(yīng)點(diǎn)對(duì)的個(gè)數(shù)；、分別為旋轉(zhuǎn)、平移變換矩陣。

3 實(shí)驗(yàn)結(jié)果與分析

本文以斯坦福大學(xué)三維點(diǎn)云庫(kù)中Bunny模型為例，詳細(xì)分析本文方法在實(shí)驗(yàn)中的具體步驟，并以斯坦福大學(xué)點(diǎn)云集中的Dragon、Happy Buddha以及Kinect采集的石膏像模型為例，將本文方法與ICP算法和Super 4PCS算法從配準(zhǔn)效果和計(jì)算效率上做以對(duì)比。實(shí)驗(yàn)環(huán)境如下：

(1) 電腦配置：Intel Core i7-4790 CPU/8 G，RAM/AMD Radeon R7 250顯卡/無(wú)GPU加速；

(2) 數(shù)據(jù)集來(lái)源：斯坦福大學(xué)點(diǎn)云集；

(3) 算法實(shí)現(xiàn)：PCL點(diǎn)云庫(kù)/C++語(yǔ)言。

斯坦福兔子掃描數(shù)據(jù)Bunny000和Bunny045模型在初始狀態(tài)下的位置關(guān)系如圖7(a)所示，Bunny000和Bunny045是對(duì)同一個(gè)兔子模型分別從0°和45°掃描得到的點(diǎn)云數(shù)據(jù)，兩片點(diǎn)云間含有部分不共有的數(shù)據(jù)。

圖7 實(shí)驗(yàn)步驟

在粗配準(zhǔn)過(guò)程中：首先對(duì)圖7(a)中的點(diǎn)分別計(jì)算其FPFH值，根據(jù)設(shè)定的閾值選擇特征相近的點(diǎn)作為對(duì)應(yīng)點(diǎn)對(duì)。圖7(b)的連線為根據(jù)閾值篩選出的對(duì)應(yīng)點(diǎn)對(duì)之間的連線，該對(duì)應(yīng)關(guān)系并不完全正確。圖7(c)為通過(guò)RANSAC步驟濾除誤匹配后得到的對(duì)應(yīng)關(guān)系。

在精配準(zhǔn)步驟中：首先通過(guò)KD-tree搜索的方式找出特征點(diǎn)對(duì)半徑鄰域內(nèi)的點(diǎn)，如圖7(d)所示，圖中的亮點(diǎn)為特征點(diǎn)，附近的點(diǎn)為其鄰域點(diǎn)。圖7(e)為選取圖7(d)中的點(diǎn)分別作為目標(biāo)點(diǎn)集和參考點(diǎn)集通過(guò)ICP算法進(jìn)行配準(zhǔn)得到的結(jié)果，圖7(f)為在原始點(diǎn)云上應(yīng)用圖7(e)計(jì)算出的變換矩陣、得到的配準(zhǔn)結(jié)果。

為驗(yàn)證本文方法的魯棒性，選取了3種共計(jì)5組各具特色的模型進(jìn)行實(shí)驗(yàn)。Stanford 點(diǎn)云集中的Dragon模型表面曲率變化較大且具有豐富的細(xì)節(jié)，選取Dragon中的Dragon0與Dragon24兩幀數(shù)據(jù)在掃描時(shí)有24°的旋轉(zhuǎn)，因此含有部分點(diǎn)云不共有的點(diǎn)。在此基礎(chǔ)上將Dragon24模型分別沿、、軸旋轉(zhuǎn)30°，平移0.05 m，模型位置關(guān)系如圖8(a)所示。

圖8(b)為本文方法的配準(zhǔn)結(jié)果，圖8(c)、8(d)分別為ICP和Super4PCS算法的配準(zhǔn)結(jié)果。

圖9的數(shù)據(jù)來(lái)源為Dragon模型中的Dragon0與Dragon48兩幀數(shù)據(jù)，二者掃描時(shí)的角度差為48°，相比于圖9中的數(shù)據(jù)，Dragon0與Dragon48的重疊區(qū)域更少。在此基礎(chǔ)上，將Dragon48模型分別沿著、、軸旋轉(zhuǎn)60°，平移0.1 m，得到圖9(a)所示位置關(guān)系。圖9(b)~(d)分別為本文算法、ICP算法和Super4PCS算法的實(shí)驗(yàn)結(jié)果。

與Dragon相比，Happy Buddha模型表面曲率變化相對(duì)平緩，但缺乏細(xì)節(jié)。圖10中的數(shù)據(jù)來(lái)源為Happy Buddha模型中相鄰的兩幀數(shù)據(jù)Happy Buddha0與Happy Buddha24。

圖8 Dragon0和Dragon24數(shù)據(jù)對(duì)比結(jié)果(下行為俯視圖)

圖9 Dragon0和Dragon48數(shù)據(jù)對(duì)比結(jié)果

圖10 Happy Buddha0和Happy Buddha24數(shù)據(jù)對(duì)比結(jié)果(下行為俯視圖)

Happy Buddha0與Happy Buddha24在掃描時(shí)的旋轉(zhuǎn)角度為24°，在此基礎(chǔ)上，將Happy Buddha24分別沿著、、軸旋轉(zhuǎn)90°，平移0.15 m，得圖10(a)中的初始位置關(guān)系。圖10(b)~(d)分別為各算法對(duì)比結(jié)果。

圖11中的數(shù)據(jù)來(lái)源為Happy Buddha模型中的Happy Buddha0與Happy Buddha48兩幀數(shù)據(jù)，二者在掃描時(shí)的旋轉(zhuǎn)角度為48°，相較于圖11中的模型，重疊的點(diǎn)云數(shù)據(jù)更少。在此基礎(chǔ)上，將Happy Buddha48模型分別沿、、軸旋轉(zhuǎn)120°，平移0.2 m，位置關(guān)系如圖11(a)所示，圖11(b)為本文算法配準(zhǔn)結(jié)果，圖11(c)為ICP算法配準(zhǔn)結(jié)果，圖11(d)為Super4PCS算法的配準(zhǔn)結(jié)果。

圖11 Happy Buddha0和Happy Buddha48數(shù)據(jù)對(duì)比結(jié)果(下行為俯視圖)

圖12中的數(shù)據(jù)為手持Microsoft Kinect相機(jī)在隨機(jī)角度上采集的兩幀點(diǎn)云數(shù)據(jù)，點(diǎn)云未經(jīng)濾波去噪等處理，初始位置如圖12(a)所示。

圖12(b)為本文算法配準(zhǔn)結(jié)果，圖12(c)為ICP算法的結(jié)果，圖12(d)為Super4PCS算法的結(jié)果。

表1為本文算法與ICP算法和Super4PCS算法的對(duì)比結(jié)果。從圖8~12中可以看出，ICP算法配準(zhǔn)大角度變化點(diǎn)云容易陷入局部最優(yōu)，從而導(dǎo)致配準(zhǔn)失敗。在對(duì)表1第一組數(shù)據(jù)Dragon0和Dragon24的配準(zhǔn)中，相比于ICP算法，本文算法的RMS值降低了75.2%，相比于Super4PCS算法RMS值降低了42.0%，在時(shí)間花費(fèi)上，本文算法花費(fèi)時(shí)間高于ICP算法14.2%，但由于ICP算法配準(zhǔn)失敗，該數(shù)據(jù)不具有參考價(jià)值，Super4PCS所用時(shí)間為本文算法的7倍；在第二組數(shù)據(jù)中，本文算法的RMS相比于ICP和Super4PCS算法分別降低了62.2%、15.2%，花費(fèi)時(shí)間為Super4PCS算法的11.8%；在第三組數(shù)據(jù)中，本文算法的RMS相比于ICP和Super4PCS算法分別降低了64.3%、36.1%，花費(fèi)時(shí)間為Super4PCS算法的16.6%；在第四組數(shù)據(jù)中，本文算法的RMS相比于ICP和 Super4PCS算法分別降低了46.8%、6.5%，花費(fèi)時(shí)間為Super4PCS算法的2.9%；在第五組數(shù)據(jù)中，本文算法的RMS相比于ICP和 Super4PCS算法分別降低了50.0%、6.3%，花費(fèi)時(shí)間為Super4PCS算法的30.4%。綜上所述，本文算法能夠有效解決大角度變換點(diǎn)云的配準(zhǔn)問(wèn)題，并得到相對(duì)優(yōu)于ICP和Super4PCS算法的結(jié)果。

圖12 Kinect采集數(shù)據(jù)隨機(jī)兩幀對(duì)比結(jié)果(下行為俯視圖)

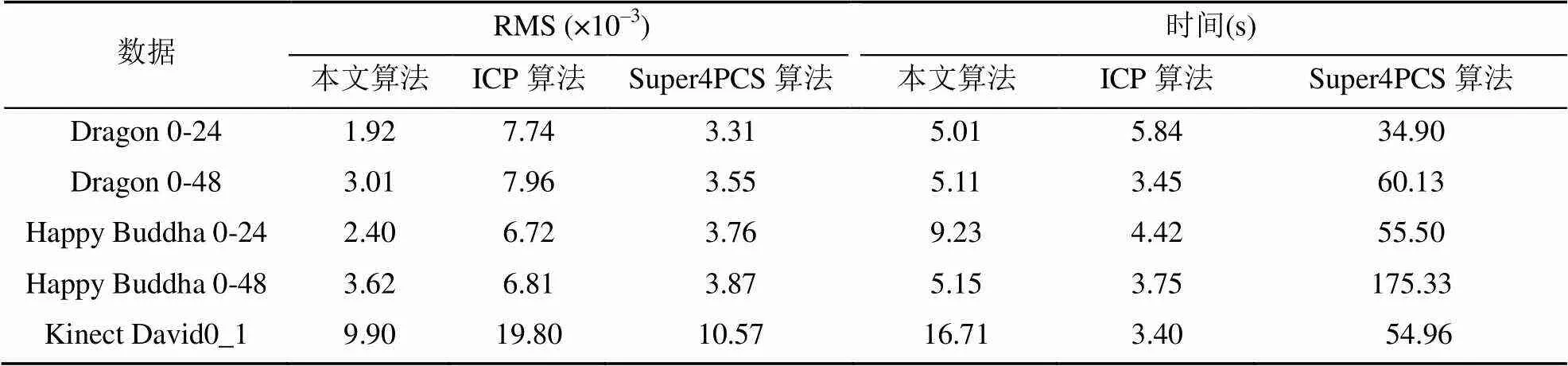
表1 算法對(duì)比表

4 結(jié)束語(yǔ)

本文通過(guò)總結(jié)和分析點(diǎn)云數(shù)據(jù)配準(zhǔn)算法的研究現(xiàn)狀，發(fā)現(xiàn)了點(diǎn)云配準(zhǔn)中存在的大變換角度點(diǎn)云難以配準(zhǔn)這一問(wèn)題，提出了一種基于精確對(duì)應(yīng)特征點(diǎn)對(duì)及其鄰域點(diǎn)云的配準(zhǔn)方法。通過(guò)利用點(diǎn)云的特征信息找出初始對(duì)應(yīng)關(guān)系，再濾除掉錯(cuò)誤對(duì)應(yīng)點(diǎn)對(duì)得到粗配準(zhǔn)結(jié)果，在此基礎(chǔ)上選擇精確對(duì)應(yīng)點(diǎn)對(duì)鄰域點(diǎn)云計(jì)算最優(yōu)收斂。實(shí)驗(yàn)表明，該方法能夠在節(jié)約計(jì)算成本的同時(shí)有效解決大角度變換、只有部分重合點(diǎn)云的配準(zhǔn)問(wèn)題。

[1] BESL P J, MCKAY N D. A method for registration of 3-D shapes [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-256.

[2] 趙夫群, 周明全. 改進(jìn)的概率迭代最近點(diǎn)配準(zhǔn)算法[J]. 圖學(xué)學(xué)報(bào), 2017, 38(1):15-22.

[3] RUSU R B, MARTON Z C, BLODOW N, et al. Learning informative point classes for the acquisition of object model maps [C]//International Conference on Control, Automation, Robotics and Vision. New York: IEEE Press, 2008: 643-650.

[4] RUSU R B, BLODOW N, BEETZ M. Fast point feature histograms (FPFH) for 3D registration [C]//IEEE International Conference on Robotics and Automation. New York: IEEE Press, 2009: 3212-3217.

[5] 馬大賀, 劉國(guó)柱. 改進(jìn)的基于FPFH特征配準(zhǔn)點(diǎn)云的方法[J]. 計(jì)算機(jī)與現(xiàn)代化, 2017(11):46-50.

[6] AIGER D, MITRA N J, COHEN-OR D. 4-points congruent sets for robust pairwise surface registration [J]. Acm Transactions on Graphics, 2008, 27(3):1-10.

[7] 余文利, 周明全, 稅午陽(yáng),等. 基于曲率的點(diǎn)云自動(dòng)配準(zhǔn)方法[J]. 系統(tǒng)仿真學(xué)報(bào), 2015, 27(10):2374-2379.

[8] MELLADO N, AIGER D, MITRA N J. Super 4PCS fast global pointcloud registration via smart indexing [J]. Computer Graphics Forum, 2015, 33(5):205-215.

[9] CHUM O, MATAS J, KITTLER J. Locally optimized RANSAC [C]//Joint Pattern Recognition Symposium. Berlin: Springer, 2003:236-243.

[10] RUSU R B, COUSINS S. 3D is here: point cloud library (PCL) [C]//IEEE International Conference on Robotics and Automation. New York: IEEE Press, 2011:1-4.

[11] ANGELO L D, GIACCARI L. An efficient algorithm for the nearest neighbourhood search for point clouds [J]. International Journal of Computer Science Issues, 2011, 8(5):1-11.

A Registration Method for Large-Angle PointClouds

LI Jian1, YANG Jingru1, HE Bin2

(1. School of Electrical and Information Engineering, Shaanxi University of Science & Technology, Xi’an Shaanxi 710021, China; 2. School of Electronics and Information Engineering, Tongji University, Shanghai 201804, China)

To the problem of traditional registration algorithm are difficult to get the desired effect in large-angle pointcloud registration. We proposed a registration method based on exact correspondence feature point pairs and its-neighbour pointclouds. Firstly, calculate the FPFH of the pointclouds separately, establishing correspondences between point clouds According to the eigenvalues; Then remove the erroneous matching point pairs by RANSAC, and obtain a relatively accurate set of feature point pairs; Moreover, using KD-tree search get the-Rad region of the feature point pairs respectively, and applying ICP to obtain the optimal convergence of pointclouds. Finally, applying the ICP relative position relationship to the original pointclouds to get the final registration result. Through registration testing and comparison of the Stanford Dragon, Happy Buddha pointcloud models, and Gypsum data scanned by Kinect, The experiment shows that this method can effectively solve the registration problem of pointclouds with large angle transformation, its a 3D pointclouds registration method with high accuracy and robustness.

pointcloud registration; fast point feature histograms; random sample consensus; iterative closest point; KD-tree

TP 391

10.11996/JG.j.2095-302X.2018061098

A

2095-302X(2018)06-1098-07

2018-03-26；

2018-04-18

國(guó)家自然科學(xué)基金項(xiàng)目(51538009)；陜西省工業(yè)攻關(guān)項(xiàng)目(2015GY044）

李 健(1975-)，男，陜西蒲城人，教授，博士，碩士生導(dǎo)師。主要研究方向?yàn)橛?jì)算機(jī)視覺(jué)、計(jì)算機(jī)圖形學(xué)。E-mail：lijian@sust.edu.cn

何 斌(1975-)，男，安徽安慶人，教授，博士，博士生導(dǎo)師。主要研究方向?yàn)樾滦蜋C(jī)器人動(dòng)力學(xué)及智能控制、多種傳感器技術(shù)與數(shù)據(jù)網(wǎng)絡(luò)集成應(yīng)用、大型復(fù)雜機(jī)構(gòu)動(dòng)力學(xué)與在線監(jiān)測(cè)、圖像檢測(cè)與識(shí)別技術(shù)及應(yīng)用。E-mail：hebin@tongji.edu.cn