一類改進Chua系統隱藏吸引子研究

袁運 李庶民

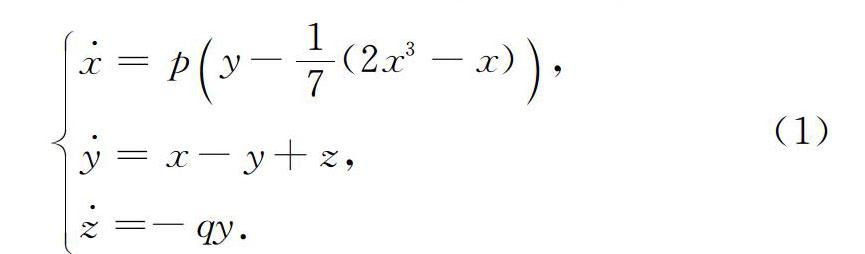
摘要：對一類改進的Chua系統進行定位系統的隱藏吸引子研究。首先，通過對改進的Chua系統平衡點穩定性進行分析，確定系統在一定條件下有一對純虛特征根。由于存在一對純虛特征根，系統在平衡點處就會出現Hopf分支。然后，通過描述對原系統進行變換，以引入一系列連續函數序列對系統進行解析數值算法迭代，與定位穩定周期解的諧波線性化方法結合定位原系統的隱藏吸引子。通過MATLAB數學軟件進行數值模擬得到系統的Lyapunov指數譜和分岔圖，從而為隱藏吸引子的存在性提供依據。運用相關程序在MATLAB的幫助下制作出系統的隱藏吸引子相圖，得出在這類改進的Chua系統中存在隱藏吸引子的結論。

關鍵詞：平衡點;改進Chua系統;Hopf分支;解析數值;諧波線性化;隱藏吸引子

Hidden Attractor of a Modified Chua System

YUAN Yun，?LI Shu?min

（College of Science， Kunming University of Science and Technology， Kunming 650500， China）

Abstract：Firstly， by discussing the stability of the equilibrium point of the improved Chua system， we can determine that the system has a pair of pure imaginary eigenvalues under certain conditions. By describing the transformation of the original system and introducing a series of continuous function sequences to iterate the analytical numerical algorithm of the system， and combining with the harmonic linearization method to locate the stable periodic solution， the hidden attractor of the original system is located. Then， the Lyapunov?exponential spectrum and bifurcation diagram?of the system is obtained by numerical simulation with MATLAB software， which provides the possibility for the existence of hidden attractor. Then， with the help of Matlab， the phase diagram of hidden attractor is obtained. Finally， it is concluded that hidden attractor exists in this improved Chua system.

Key Words：equilibrium point; modified Chua system; Hopf bifurcation; analytical numerical; harmonic linearization; hidden attractor

0?引言

過去幾十年來，動力系統的吸引子是一個熱門研究課題。眾多學者研究了經典的Lorenz[1]、Chua[2]、Rossler[3]、Chen[4]系統等著名系統的普通吸引子。這類吸引子都是由不穩定平衡點激發的（自激吸引子），在某些動力系統[5?6]中能夠從Hopf分支中得到穩定的極限環和混沌吸引子。研究這些吸引子需要用一種標準的數值方法，從平衡點鄰域中不穩定流形上的一點出發，經過一段時間的軌道運行得到吸引子并確定它。

Leonov等[7?9]提出隱藏吸引子概念，給出一整套找到隱藏吸引子的新的數值分析方法，并率先發現Chua系統中存在隱藏吸引子，通過數值模擬得到其軌線。這項研究結果昭示了有別于典型吸引子（如Lorenz、Chua、Rossler、Chen系統中的吸引子）的另一類吸引子。這類吸引子的吸引域不包含平衡點鄰域，且不能用研究經典吸引子的方法得出這類吸引子。因此，對隱藏吸引子的局部數值計算和分析研究很難。Leonov等[10?13]研究的Chua系統提出并使用了一類特殊的解析數值方法定位隱藏吸引子，并通過數學方法得到隱藏吸引子的幾何形態。隨著Leonov等人對于隱藏吸引子的研究，一些學者開始在Chua系統基礎上進行各類隱藏吸引子存在性研究。

Yassen [14]研究了其中一種改進的Chua系統：

其中，?p>0和q>0是系統（1）的系數，x和y表示通過兩個電容器的電壓，z?表示通過電阻的電流，Yassen主要利用這一系統研究自適應控制和自適應同步。

本文將Yassen的Chua系統（1）作了改進，變為如下更一般的系統：

其中，?α，β，μ，ν，l均是正數。當μ=17，ν=2，l=1時，系統（2）就是系統（1）。將α?作為分支參數研究系統（2）的Hopf分支。與系統（1）相比，系統（2）有相對復雜的動力學性質，包括周期軌道和隱藏吸引子。

1?不變性、平衡點與Hopf分支

1.1?對稱性與不變性

在坐標變換?（x，y，z）→（-x，-y，-z）?下，系統（2）保持不變，即系統（2）關于原點對稱。

1.2?平衡點穩定性分析

當?α，β，μ，ν，l均為正數時，系統（2）有3個平衡點：O（0，0，0），S?±±νν，0，l·νν。

平衡點O和S?±的穩定性如下：

（1）平衡點O?所對應的特征方程如下：

其中，?p?1=1-αμ，q?1=β-αμ-lα，r?1=-αβμ?，式（3）可以寫為：

由?α，β，μ，ν，l均為正數可知r?1<0，p?1，q?1?不一定大于0。根據Routh-Hurwitz判據可知，平衡點?O（0，0，0）不穩定。

（2）在坐標變換（x，y，z）→（-x，-y，-z）下，系統（2）保持不變，從而系統（2）關于原點對稱，因而對于S?±的穩定性只需考慮S?+的穩定性即可。

作線性變換x-=x-νν，y-=y，z-=z+l·νν，系統（2）變為：

系統（2）的平衡點S?+，其實就是系統（5）的平衡點?O?（0，0，0），它所對應的特征方程為：

令?p?2=1+2αμ，q?2=β+2αμ-lα，r?2=2αβμ?，式（6）變為：

由Routh-Hurwitz判據可得到：

引理1?由于p?2>0，r?2>0，若p?2q?2-r?2>0，則方程（7）的特征根具有負實部。

定理1?平衡點S?±?漸進穩定，當且僅當特征方程（7）的根具有負實部。

引理2?若系統（2）出現Hopf分支，則特征方程（7）有一個實根?λ?1=-（2αμ+1），和一對共軛純虛根λ?2，3=±ωi（ω>0）。

1.3?Hopf分支

由于平衡點?O（0，0，0）不穩定，因此只需討論從S?±分岔出的周期軌。等式（7）至少有一個負根，若等式（7）有一對共軛純虛根λ=±ωi（ω>0），代入方程（7）可分離出虛部與實部， ω?滿足：

將α作為分支參數，因而臨界值α?c滿足f（λ?1）=f（-（2αμ+1））=0，即

整理后得：

注意到?α>0，得到以下結論：

（1）當2μ=l時，式（9）無正根。

（2）當2μ>l時，式（9）的兩個根α?1，α?2同號，且均為負根。

（3）當2μ<l時，式（9）的兩個根α?1，α?2異號，且其中一個為正根。

由此可知，當2μ<l時，方程（9）有正根，且

其中Δ=（?2μ-l）?2-8βμ（2μ-l）。

若2μ<l，當α<α?c時，方程（7）有一對純虛根λ=±ωi，從等式（7）中可得：

將λ（α?c）=iω代入式（11）中得：

從式（8）的第二個等式可以得到：

所以β>ω?2。若2μ<l成立，則

從而得到定理2。

定理2?若?2μ<l，且α?c由式（10）定義，當α經過α?c時，系統（2）在平衡點S?±?處經歷Hopf分支。

2?隱藏吸引子定位算法

利用文獻[7?13]的算法定位系統（2）的隱藏吸引子。

2.1?算法思想

系統如下[15?17]：

其中，Ρ是n×n階常數矩陣，q和r是n維向量，是轉置，ψ（σ）是標量函數，且ψ（0）=0。

定義諧波線性化系數k，使矩陣

具有一對純虛特征值λ=±ω?0i（ω?0>0），且其余特征值均具有負實部。假設k存在，則原系統（12）變為

其中?φ（σ）=ψ（σ）-kσ。

可引入一個有限的連續函數序列φ?0（σ），φ?1（σ）…φ?m（σ），且每相鄰兩個函數φ?j（σ）與φj+1（σ）的差別較小，函數φ?0（σ）的值最小，且φ?m（σ）=φ（σ）。

由于函數φ?0（σ）最小，因此對系統進行諧波線性化：

確定一個穩定的非奇異的周期解?x?0（t）。

為確定出原系統（12）的吸引子，隨著j的增大對周期解x?0（t）進行逐步演化，記x?0（t）為Α?0的起始振蕩吸引子（不包含平衡點的吸引子）。此時可能會存在兩種情況：

（1）Α?0的所有點都位于Α?1的吸引域中，Α?1是系統

在?j=1的情形下的振蕩吸引子。

（2）當系統（15）過渡到j=1時的系統（16）時，由于不穩定分支破壞周期解而導致Α?0消失。

在第（1）種情況下，把x?0（0）作為初始點計算當j=1時系統（16）的解x?1（t）。如果x?1（t）不會趨近于平衡點，同樣也不會趨近于無窮遠（要考慮充分大的程序運行區間[0，T]），則x?1（t）進入到吸引子Α?1中。再執行j=2時系統（16）的情況，將x?2（0）=x?1（T）作為初始點，經過充分長的一段運行時間t之后得到當j=2時系統（16）的解x?2（t）。

繼續執行以上程序，且逐漸增大j，取x?j（0）=xj-1（T）為初始點，可找到當j=m時系統（16）（即原系統（12））的解x?j（t），或在運算某一步中不穩定分支破壞周期解。

2.2?穩定周期解定位算法

由于要充分考慮到系統[18?20]中存在非線性項，所以將系統（14）改寫為：

其中，Ρ?0是n×n階常數矩陣，q和r是n維向量，φ（σ）為連續函數且滿足φ（0）=0，k為諧波線性化系數，使得Ρ?0有一對純虛特征根λ=±ω?0i（ω?0>0），其余均有負實部。

通過非退化線性變換，可將系統（17）化簡為：

其中?y?3，b?3，c是n-2維向量，b?1，b?2為實數;A是（n-2）×（n-2）?階矩陣，其余特征根均具有負實部。

系統（17）的變換函數為：

系統（18）的變換函數為：

其中η，θ為實數，Q（p）為n-2次多項式，R（p）為低于n-2次的多項式。設Q（p）與R（p）沒有相同的根。由于系統（17）和（18）等價，則變換函數（19）與（20）相等，得到如下關系式：

定義描述函數

定理3[8?9]?若存在一個正數a?0，使a?0滿足：

對于充分小的ε>0，則系統（17）具有初始條件x?0（0）=S（y?1（0），y?2（0），y?3（0））?的周期解x?0（t），其中

y?1（0）=a?0+O（ε），y?2（0）=0，y?3（0）=O?n-2（ε），且O?n-2（ε）是n-2維向量，其它分量為O（ε）。

定理3保證了通過諧波線性化方法結合迭代算法尋找穩定周期解的可行之處，也保證了定位隱藏吸引子的可能性。

采用上述算法思想[15?17，20]定位系統（2）的隱藏吸引子。首先將系統（2）改寫為類似系統（12）的形式：

其中

接著考慮引入諧波線性化系數?k和一個小參數ε?，并把系統（21）改寫為如下形式：

其中

并且矩陣?Ρ?0的特征根滿足：

λΡ?0?1，2=±iω?0，λ?3=-d<0

通過非退化線性變換?x=Sy?，可將系統（23）轉化為如下形式：

其中

A=0-ω?00?ω?000?00-d，b=b?1?b?2?1，u=1?0?-δ

系統（22）的變換函數?W?H（p）?可以表示為：

由于系統（22）與系統（23）具有等價性，因此可得到系統（23）的變換函數：

W?H（p）=r?（Ρ?0-pI）-1q

其中?p是復變量，且初始振蕩頻率ω?0?由公式lm?W?H（iω?0）=0決定，諧波線性化系數k由公式k=-（?Re?W?H（iω?0））-1決定，則得到以下關系式：

由于系統（23）是系統（21）通過非退化線性變換x=Sy得到的，因此矩陣S滿足：

設矩陣

于是可得：

s?11=1，s?12=0，s?13=-δ

s?21=-（μ+k），s?22=-ω?0α，s?23=δ（d+α（μ+k））α

s?31=-βα，s?32=β（μ+k）ω?0，s?33=βδ（d+α（μ+k））dα

對于充分小的ε，可得到以下初始值：

作為定位隱藏吸引子算法的第一步初始值，由式（25）可得系統（22）與系統（23）的初始值之間的關系為：

再回到系統（2），可以確定其初始值為：

其中a?0可由描述函數Φ（a）確定，描述函數滿足Φ（a?0）=0且dΦ（a）da?a=a?0≠0。

3?數值模擬

分別取l=1.4，μ=0.25，ν=6和β=300?。利用MATLAB軟件可作出相應的相圖，最大值法可畫出系統的分支圖，且Lyapunov指數譜可由Wolf[21]中提到的程序得到。

3.1?由不穩定平衡點出現的吸引子

當取上述參數值時，系統（2）有3個平衡點，?分別為O（0，0，0）和S?±（±0.408 2，0，0.571 5）。前述已得出O（0，0，0）總是不穩定的，通過簡單計算，可以看到2μ=0.5<l=1.4，因而可以得到臨界值α?c=24.839 2在系統（2）中有兩個純虛特征值。平衡點S?±在α∈（0，α?c）穩定，且在α>α?c上失去穩定性。當α>α?c?時，系統（2）將呈現更為復雜的動力學行為。

圖1顯示對于系數α系統（2）的Lyapunov指數譜。當?α?∈（10，24.839 2）時，最大的Lyapunov指數總為負值。且由圖2中可見，當?α?∈（10，24.839 2）時，從S?±中不能分支出周期軌且S?±總是穩定的。

當?α?∈（24.839 2，50）時，最大的Lyapunov指數接近于零，意味著系統（2）有周期軌。圖2顯示當?α過渡到α?c=24.839 2時，能從S?±中分支出周期軌，且當α?∈（50，80）時，最大的Lyapunov指數總是為正值。這表明隨著α值的增大，系統（2）通過分支達到混沌。

注意所有的吸引子都是從平衡點分支而來，因此計算吸引子需要從平衡點的小鄰域中的某一初始值去計算。

3.2?隱藏吸引子

在上述的數值模擬中，吸引子是在平衡點S?±的鄰域中不穩定流形上的一點出發的。在圖（3）中，通過上述算法可以探測出初始值，且由這些初始值出發的軌道不會縮減至?O或S?±。也就是說，吸引子不會在S?±的鄰域中不穩定流形上的點開始，即吸引子是隱藏的。

（a）α=20 （b））α=30 （b））α=30

（c）α=65

圖3（a）-圖3（c）顯示隨著?α?值的變化隱藏吸引子的不同情況。圖3（a）顯示S?±穩定，且當?α=20時，隱藏吸引子圍繞在S?±周圍;圖3（b）顯示S?±不穩定，且當α=30時，隱藏吸引子圍繞在S?±分支出的周期軌周圍;圖3（c）顯示?S?±周圍出現混沌，且當α?=65時，隱藏吸引子圍繞在混沌軌道周圍。

從上面的數值結果可見，隱藏吸引子由平衡點分支而來。通過數值模擬能夠定位并發現隱藏吸引子，即這個改進的Chua系統中存在隱藏吸引子。

4?結語

通過對改進Chua系統隱藏吸引子研究，可以看出這一系統符合解析數值算法，即引入一對連續的函數序列不斷進行迭代，并利用無限逼近的方法逐漸接近原系統進而得到原系統的解。對于系統穩定周期解的定位其實就是對原系統進行非退化變換，得到的系統具有一對純虛特征根，其余特征值均具有負實部。變換前后的函數對應值相同，并且通過諧波線性化得到穩定周期解，它的初始值必須滿足定理3。通過MATLAB畫出lyapunov指數譜、分岔圖和相圖，可以看出隱藏吸引子存在于這一系統中。

本文存在以下不足：對于隱藏吸引子存在于這一系統只是滿足解析數值算法，無法在理論上證明出隱藏吸引子與平衡點鄰域不相交。因此，針對隱藏吸引子與平衡點鄰域不相交的問題是下一步研究的重點。

參考文獻：

[1]?LORENZ E N. Deterministic nonperiodic flow [J]. Journal of The Atmospheric Sciences， 1962（20）：130?141.

[2]?ROSSLER O E. An equation for continuous chaos[J]. Physics Letters A， 1976， 57（5）： 397?398.

[3]?CHUA L O， LIN G N. Canonical realization of chua's circuit family[J]. IEEE Transactions on Circuits & Systems， 1990， 37（7）： 885?902.

[4]?CHEN G R， UETA T. Yet another chaotic attractor[J]. International Journal Of Bifurcation & Chaos， 1999，9（7）：1465?1466.

[5]?QI G， CHEN G， DU S， et al. Analysis of a new chaotic system[J]. Physica A Statistical Mechanics & Its Applications， 2012， 352（2）： 295?308.

[6]?JING Z， YANG J， FENG W. Bifurcation and chaos in neural excitable system[J]. Chaos Solitons & Fractals， 2006， 27（1）： 197?215.

[7]?KUZNETSOV N V， LEONOV G A， VAGAITSEV V I. Analytical?numerical method for attractor localization of generalized chua's system[J]. Ifac Proceedings Volumes， 2010， 43（11）： 29?33.

[8]?LEONOV G A， VAGAITSEV V I， KUZNETSOV N V. Algorithm for localizing Chua attractors based on the harmonic linearization method[J]. Doklady Mathematics， 2010， 82（1）： 663?666.

[9]?LEONOV G A， KUZNETSOV N V， KUZNETSOVA O A， et al. Hidden oscillations in dynamical systems[J]. Wseas Transactions On Systems & Control， 2011， 6（2）： 54?67.

[10]?LEONOV G A， KUZNETSOV N V. Analytical?numerical methods for investigation of hidden oscillations in nonlinear control systems[J]. Ifac Proceedings Volumes， 2011， 44（1）： 2494?2505.

[11]?LEONOV G A， KUZNETSOV N V， VAGAITSEV V I. Localization of hidden Chua attractors[J]. Physics Letters A， 2011，375（23）：2230?2233.

[12]?LEONOV G A， KUZNETSOV N V， VAGAITSEV V I. Hidden attractor in smooth Chua systems[J]. Physica D Nonlinear Phenomena， 2012， 241（18）： 1482?1486.

[13]?KUZNETSOV N V， KUZNETSOVA O A， LEONOV G A， et al. Hidden attractor in Chua's circuits[C].8th International Conference on Informatics in Control， Automation and Robotics. 2011： 279?283.

[14]?YASSEN M T. Adaptive control and synchronization of a modified Chua's circuit system[J]. Applied Mathematics & Computation， 2003， 135（1）： 113?128.

[15]?LEONOV G A， KUZNETSOV N V. Hidden oscillations in dynamical systems. 16 hilbert′s problem， Aizerman′s and Kalman′s conjectures， hidden attractors in Chua′s circuits[J]. Journal Of Mathematical Sciences， 2014， 201（5）： 645?662.

[16]?KUZNETSOV N V， LEONOV G A. Hidden attractors in dynamical systems： systems with no equilibria， multistability and coexisting attractors[J]. IFAC Proceedings Volumes， 2014， 47（3）： 5445?5454.

[17]?LEONOV G A， KISELEVA M A， KUZNETSOV N V， et al. Discontinuous differential equations： comparison of solution definitions and localization of hidden Chua attractors[J]. Ifac Papersonline， 2015， 48（11）： 408?413.

[18]?DUDKOWAKI D， JAFARI S， KAPITTANIAK T， et al. Hidden attractors in dynamical systems[J]. Physics Reports， 2016， 637： 1?50.

[19]?LEONOV G A， KUZNETSOV N V. Hidden attractors in dynamical systems from hidden oscillations in Hilbert?Holmogorov， Aizerman， and Kalman problems to hidden chaotic attractor in Chua circuits[J]. International Journal Of Bifurcation & Chaos， 2013， 23： 1330002.

[20]?TESI A， VICINO A. Robust absolute stability of lur'e control systems in parameter space[M]. Pergamon Press， Inc. 1991， 27（1）： 147?151.

[21]?WOLF A， SWIFT J B， SWINNEY H L， et al. Determining Lyapunov exponents from a time series[J]. Physica D Nonlinear Phenomena， 1985， 16（3）： 285?317.