基于隔離度特性的導引頭控制系統優化設計

劉石祥, 杜 肖, 符勝楠, 夏群利

(1. 北京理工大學機電學院, 北京 100081; 2. 中國運載火箭技術研究院, 北京 100076; 3. 北京理工大學宇航學院, 北京 100081)

0 引 言

導引頭控制系統不僅要快速跟蹤目標,同時還要隔離彈體擾動。隔離度表征了導引頭隔離彈體擾動的能力,不僅影響視線角速度的輸出精度,同時在制導回路中形成隔離度寄生回路[1-3],影響制導系統的穩定性和制導精度[4-5]。

文獻[6]建立了平臺導引頭隔離度模型。文獻[7]利用隔離度簡化模型對寄生回路穩定性進行了研究。文獻[8]研究平臺導引頭隔離度對制導系統的影響。為了降低隔離度,很多學者進行了隔離度抑制補償技術進行研究,文獻[9]研究了基于無跡卡爾曼濾波的捷聯導引頭隔離度補償方法,文獻[10]采用強跟蹤無跡卡爾曼濾波對半捷聯導引頭隔離度進行在線補償。文獻[11]通過估計干擾實現前饋解耦,有效抑制了導引頭隔離度。文獻[12-13]設計了擾動觀測器對彈目視線角速度進行估計并輸出到制導系統中,實現對隔離度的抑制。文獻[14-15]則是基于干擾力矩模型,對干擾力矩系數進行估計,從而利用干擾力矩模型對視線角速度進行補償,但是由于估計和補償算法較為復雜,其所需的估計時間較長。文獻[16]指出較寬的穩定回路帶寬能夠有效降低隔離度,但是導引頭穩定回路帶寬由于硬件限制不能無限制的增加。文獻[17]研究指出,隔離度與導引頭回路有重要關系,在導引頭穩定回路中引入合適的滯后校正網絡可顯著提高隔離度水平。

雷達導引頭跟蹤回路由于受到探測器信號積累所引起的延時的影響,其跟蹤回路帶寬設計受到限制,一般低于3 Hz,為了保證跟蹤高速機動目標,提高導引頭跟蹤快速性,需要在跟蹤回路增加超前校正網絡。目前工程上普遍使用的比例-積分-微分(proportional-integral-derivative,PID)或其變形控制器進行校正,其關鍵的問題就是控制參數的整定[18]。同時為了保證導引頭控制系統的頻域特性,需要在設計過程中考核導引頭的幅值裕度和相位裕度,文獻[19]引入了幅值-相位測試器(gain-phase margins tester,GPMT),文獻[20]進一步研究了具有時延特性的控制系統參數與頻域幅值裕度和相位裕度之間的關系。基于對穩定域的研究,用最大靈敏度函數、誤差最小二乘準則等定義目標函數,在所得到的控制參數穩定域利用尋優算法獲得控制參數[21]。

本文在保證導引頭幅值裕度和相位裕度約束下,通過對內外回路控制系統進行優化設計,使導引頭具有更好的隔離度特性和時域特性。首先建立導引頭隔離度模型,推導了隔離度傳遞函數,分析了隔離度與穩定回路和跟蹤回路的關系,確定了內外回路分別設計的方法。穩定回路以導引頭隔離度指標最優為目標函數,跟蹤回路以導引頭時域響應最優為目標函數,將幅值裕度和相位裕度轉為化對控制參數的穩定域范圍,通過分別求解穩定回路和各種回路帶約束的優化問題,得到內外回路優化設計參數。通過仿真驗證表明,設計的控制系統具有良好的時域特性,同時提高了導引頭隔離度,對導引頭控制系統設計具有比較大的參考作用。

1 平臺導引頭隔離度模型

導引頭隔離度模型如圖1所示。圖中G1(s)為導引頭跟蹤回路前向傳函,G2(s)為穩定回路前向傳函,包括校正網絡和運放,GD(s)為干擾力矩傳函,H(s)為速率陀螺傳函。該模型包括干擾力矩回路、反電勢回路、穩定回路和跟蹤回路及電流環回路。穩定回路起到空間穩定作用,跟蹤回路起到準確跟蹤的作用。干擾力矩回路是由于導引頭轉動過程中各種導線的拉扯以及轉動連接處的動靜摩擦等引起的,干擾力矩的產生將會使彈體的運動耦合進導引頭運動中,降低導引頭的控制精度,對導引頭控制是有害的。反電勢回路的和電流環一般比較小,對導引頭控制精度影響不大。

圖1 平臺導引頭隔離度模型Fig.1 Mode of disturbance rejection rate of seeker

平臺導引頭輸出視線角速度,通常既可取自角速率陀螺輸出處,又可取自穩定回路的指令輸入處,從導引頭跟蹤的角度來說,由于穩定回路響應速度非常快,所以這兩種取法基本可看作一致。但從隔離度的角度分析,這兩種取法會造成隔離度傳遞函數不一致[2]。本文從角速率陀螺處提取視線角速度信號,并建立導引頭隔離度模型。

基于傳遞函數概念給出隔離度傳遞函數RDRE(s)的定義為

(1)

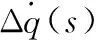
依圖1可以得到導引頭隔離度傳遞函數為

(2)

影響隔離度的干擾力矩主要有彈簧力矩和粘滯阻尼力矩[8]。令彈簧力矩系數為Kn,粘滯阻尼力矩系數為Kω,它們正比于彈簧力矩和粘滯阻尼力矩的大小。把粘滯阻尼力矩模型GD(s)=Kω和彈簧力矩模型GD(s)=Kn/s分別代入式(1)可得到在粘滯阻尼力矩和彈簧力矩作用下隔離度傳遞函數分別為

(3)

(4)

從式(3)和式(4)可以看出,不同干擾力矩作用下導引頭隔離度傳遞函數不同,導引頭隔離度并不能簡單認為是某個頻點的恒定值,隔離度的頻率特性與導引頭控制系統的頻率特性密切相關。

在對平臺導引頭隔離度傳遞函數模型進行等效簡化,忽略探測器延時環節及校正網絡的影響,令G1(s)=1,G2(s)=1,R≈1,L≈0,穩定回路等效增益K2=G2k2KT/J,跟蹤回路等效增益K1=G1k1。對圖1做等效變形可得圖2。

圖2 隔離度等效框圖Fig.2 Equivalent block of disturbance rejection rate

干擾力矩為彈簧力矩時,隔離度傳遞函數如式(5)所示,干擾力矩為阻尼力矩時,隔離度模型如式(6)所示。

(5)

(6)

從式(5)和式(6)可以看出,導引頭隔離度水平與導引頭回路參數有重要關系,由此可通過改進導引頭回路設計達到提高隔離度水平的目標。

導引頭跟蹤回路帶寬決定了導引頭跟蹤的快速性,而由于探測器延時的存在及噪聲的影響等硬件制約,導引頭的快速性與穩定性成了相互制約的關系,跟蹤回路帶寬一般限制在3 Hz以下,典型值取2 Hz。而導引頭穩定回路帶寬決定了其抗彈體擾動的能力,內回路帶寬越大隔離度特性越好,其帶寬受到電機、角速率陀螺等動力學的影響,一般可設計至30 Hz以上,遠大于導引頭跟蹤回路帶寬,從而使得導引頭控制系統內外回路之間的影響較小,可以實現導引頭內外回路分開設計。

2 導引頭優化設計流程

2.1 頻域指標約束

對于一個典型的單輸入單輸出(single input single output,SISO)單位反饋控制系統,進行控制系統設計時需要滿足期望的頻域指標,假設A為系統的幅值裕度,φ為系統相位裕度,在求取SISO控制系統滿足頻域約束的穩定域時,可借助如圖3的帶有GPMT[21]的控制系統結構圖求解。

圖3 帶有GPMT的控制系統結構Fig.3 Block of control system with GPMT

當A=1,φ為期望的相位裕度,則圖3所示系統的穩定性設計可轉變為基于相位裕度的控制參數設計;當φ=0,A為期望的幅值裕度,則圖3所示系統的穩定性設計可轉變為基于幅值裕度的控制參數設計;求取兩者的交集即可獲得基于幅值裕度和相位裕度約束的穩定域。

2.2 目標函數

幅值裕度和相位裕度是控制系統穩定性的衡量指標,在控制系統設計時,還應該導引頭抗彈體擾動能力的隔離度指標和跟蹤能力的時域響應指標,針對這兩個指標設計目標進行控制系統參數優化。

(1) 隔離度目標函數

根據工程實踐和研究[17],穩定回路增益與彈體隔離度成反比關系,通過增大穩定回路增益,可以降低導引頭隔離度。選取導引頭頻率ωa處的穩定回路開環增益最大為目標函數,使其幅值最大,則可得到當前條件下的最小隔離度。

選取穩定回路目標函數為

J=M(ωa)

(7)

用D來表示基于幅值和相位裕度約束的穩定區域,選取典型的導引頭頻率ωa=2 Hz,則約束優化問題可以描述為

(8)

(2) 時域目標函數

跟蹤回路增益對隔離度的影響比較小,主要衡量其跟蹤能力,通過時域目標函數來實現跟蹤回路優化。時域目標函數分為特征型目標函數和誤差型目標函數兩大類。誤差型目標函數采用期望響應和實際響應之差的某種表達式作為目標函數。常用的誤差型目標函數包括誤誤差平方矩的積分型(integrated time square error,ITSE)、誤差平方的積分型(integrated square error,ISE)、誤差絕對值矩的積分型(integrated time absolute error,ITAE)和誤差絕對值的積分型(integrated absolute error,IAE)。

2.3 設計流程

在求解有約束最優化問題時,可通過構造懲罰函數等方法將有約束的優化問題轉換為無約束優化問題從而進行求解,也可基于KKT(Karush-Kuhn-Tucker)方程解的方法進行求解。一般地,最優化數學模型能夠表示成下列標準形式:

(9)

表1 Etime目標函數

為了實現有約束條件下的最優值求解,要求約束的梯度向量與目標函數的梯度向量在最優解處平行。KKT算法利用拉格朗日法合并目標函數與約束,并通過求取如式(9)所示不等式組最小值點x*獲得有約束條件下的最優值。故而基于KKT法的一般約束優化問題極值點一階必要條件可表示為

(10)

式中,μi和λi為拉格朗日乘子。KKT方程是有約束優化問題的必要條件,KKT方程的解形成了許多非線性規劃算法的基礎,這些算法直接計算拉格朗日乘子,通過用擬牛頓法更新過程,給KKT方程積累二階信息,可以保證有約束擬牛頓法的超線性收斂。基于KKT方法的Fmincon函數可用于有約束非線性優化問題,可先通過Simulink搭建控制系統框圖,再利用Fmicon函數進行尋優算法。基于上述分析,導引頭優化設計流程圖如圖4所示。

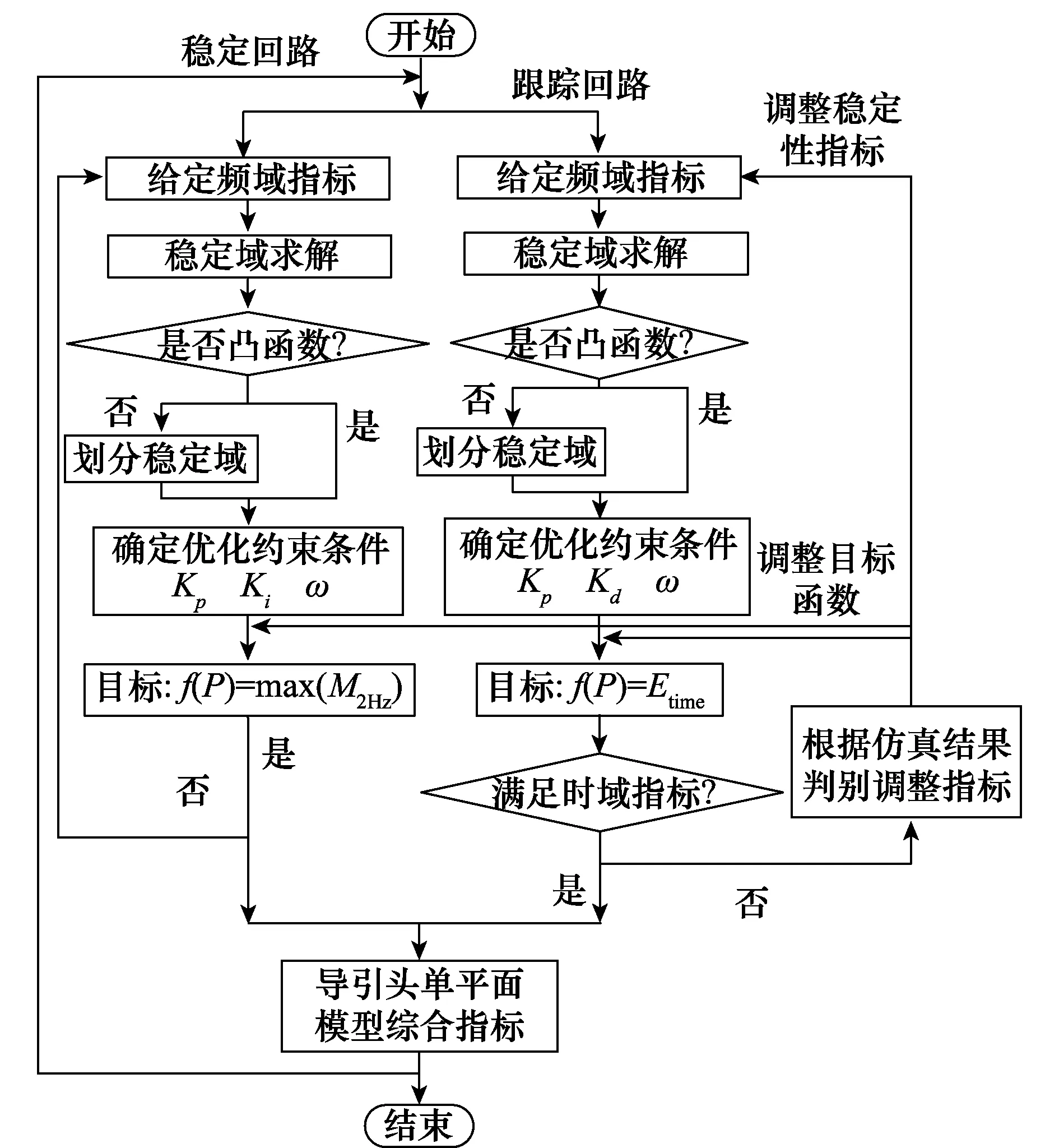
圖4 優化設計流程Fig.4 Optimization design process

3 導引頭穩定回路設計

穩定回路以關心頻率點處隔離最小為控制系統的優化目標函數,以控制系統幅值和相位裕度作為約束條件,采用PI校正網絡進行穩定回路控制系統設計,提高穩定回路中關心頻帶的增益,從而降低導引頭隔離度幅值。經過簡化得穩定回路框圖如圖5所示。

圖5 穩定回路框圖Fig.5 Stabilized loop block diagram

采用GPMT方法[21],鑒相環節為Ae-jφ,則可得到帶有GPMT的穩定回路框圖，如圖6所示。

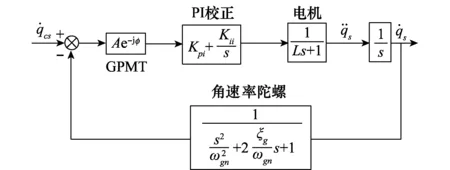
圖6 帶有GPMT的穩定回路框圖Fig.6 Stabilized loop block diagram with GPMT

穩定回路開環傳遞函數為

(11)

則穩定回路的閉環特征方程為

Ae-jφ×(Kpis+Kii)

(12)

根據線性系統判穩條件,閉環系統特征根均在左半平面,相當于式(12)無右半平面根。令s=jω,并代入式(12),并采用歐拉公式,則可獲得如式(13)所示的基于實部和虛部的特征方程表達式:

F(ω)=Fr(ω)+jFi(ω)

(13)

其實部和虛部分別表示為

(14)

可得如(15)所示的邊界條件。

(15)

故而,閉環特征方程的穩定性可以在控制參數空間(Kp,Ki)進行研究,則求解方程組(15),可得控制參數表達式為

(16)

式中

解方程組可以得到曲線(Kpi(ω),Kii(ω)),從而形成分割控制參數空間的穩定邊界如圖7所示,取角速率陀螺參數ωgn=80 Hz，ξg=0.7 。

圖7 不同幅相裕度條件下穩定域分布Fig.7 Stability region under different amplitude margin and phase margin

幅穩定裕度ΔL=6 dB,相穩定裕度條件φ=40°,同時滿足幅值和相位裕度約束時,Kpi和Kii的取值范圍為相角裕度φ=40°形成的邊界線,故而控制參數穩定域可表示為

D={Kpi(φ=40),Kii(φ=40)}

(17)

根據式(8)所示穩定回路目標函數,約束優化問題可以表示為

(18)

由圖8可知,2 Hz點幅值的極大值分布于穩定域邊界處,從而形成凸函數,有利于優化方法的使用,通過求解其極小值,獲得最優解為Kpi=181,Kii=1.0×104。

圖9 有無PI校正穩定回路開環伯德圖Fig.9 Compare of open loop Bodes for stabilized loop with PI compensator and no compensator

采用最優控制參數獲得如圖9所示有無PI校正穩定回路開環伯德圖對比。無PI校正時2 Hz點增益為22.2,采用基于幅相裕度約束的最優化控制參數時2Hz處增益為65.4,比之前提高了3倍,則隔離度水平提高3倍。

4 導引頭跟蹤回路設計

跟蹤回路以探測器跟蹤誤差角最小為目標函數,以控制系統幅值相裕度作為約束條件,采用PD校正網絡,實現快速跟蹤目標,在保證較小超調量的同時響應時間盡量短。探測器純延時取為40 ms,跟蹤回路校正網絡設計時的幅相裕度,依然采用GPMT法,如圖10所示。

圖10 有GPMT的跟蹤回路框圖Fig.10 Tracking loop block diagram with GPMT

此時,跟蹤回路開環傳遞函數為

(19)

則跟蹤回路的閉環特征方程為

(20)

利用歐拉公式,式(20)可表述為式(21)所示實部與虛部的形式。

F(jω)=Fr(ω)+jFi(ω)

(21)

其中,Fr(ω)為實部;Fi(ω)為虛部。求解

(22)

可得

(23)

式中

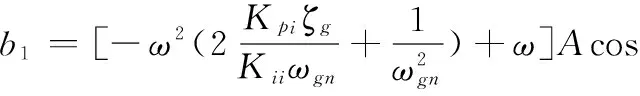
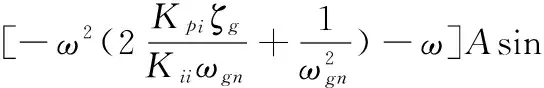
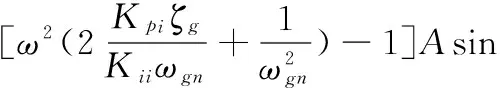
在此控制方案中,有一個微分控制器位于前向通路,另一個微分控制器位于反饋通路,將穩定回路的微分因素分配在前向通道上可以:①改善跟蹤回路的穩定裕度,在一定程度上提高跟蹤回路的帶寬;②在穩定回路特性一定的條件下改善導引頭的隔離度特性。故而可得到其穩定域的分布如圖11所示。

由圖11可知,由于導引頭跟蹤回路受到導引頭探測器信息處理延時的影響,其幅裕度對控制參數Kpo和Kdo較為敏感,而相裕度次之,故而幅裕度6 dB穩定邊界位于相裕度40°穩定域范圍之內,在后續對控制參數進行尋優時,可將約束條件設置為幅裕度6 dB。在滿足幅裕度的穩定邊界處隨著Kpo的不同,其時域特性具有明顯的差異,Kpo越大其超調量越大。

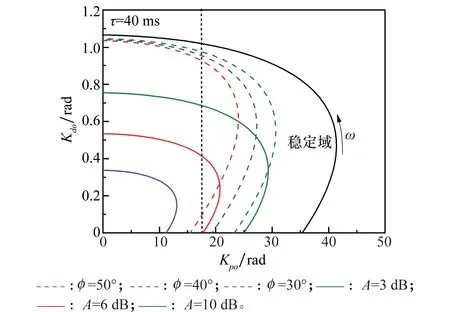
圖11 PD校正穩定域分析圖Fig.11 Analysis of stabilized region with PD

由目標函數等高線與穩定域的邊界可知,如圖12所示,控制系統參數最優點位于約束邊界與目標函數等高線相切處;當目標函數極值點位于穩定邊界以內,則控制參數最優點與約束邊界無關。

圖12 時域目標函數等高線圖Fig.12 Contour map of time domain objective functions

圖13為滿足穩定域的時域目標函數優化結果,從分布上可以看出,不同目標函數準則下的最優點基本都在穩定邊界上,滿足穩定性要求,如果進一步放開穩定裕度要求,則可得到更好的時域性能指標。

圖13 穩定域分布Fig.13 Stability region

5 導引頭控制系統仿真驗證

根據設計的穩定回路和跟蹤回路優化設計參數,代入導引頭控制系統中,進行導引頭時域性能和隔離度特性仿真驗證。導引頭控制系統框圖如圖14所示。

圖14 具有校正網絡導引頭控制系統Fig.14 Seeker control system with correction network

導引頭跟蹤時域特性仿真結果如圖15所示。從圖15可以看出,未進行超前校正時階躍響應具有比較大的超調,通過優化控制設計,降低了超調,ITAE準則下的超調最小。

圖15 導引頭時域特性Fig.15 Time domain characteristic of seeker

各準則時域優化時的結果分布較為集中,各優化結果的性能指標如表2所示。

表2 時域特性優化對比

導引頭隔離度特性仿真結果如圖16和圖17所示。仿真結果表明,采用校正網絡后隔離度水平提高了3倍,同時校正網絡的存在對隔離度的相位產生影響。通過對比分析可知,外回路設計指標采用不同誤差準則作為目標函數對隔離度影響不大,故而在后續的控制系統設計時可根據具體時域要求進行設計,而主要通過內回路設計采用隔離度的目標函數進行約束,以最大程度提高隔離度水平。

該抑制隔離度的方法通過建立以失穩頻率點處隔離最小為控制系統的優化目標函數,以控制系統幅相裕度作為約束條件,綜合考慮導引內外回路進行設計,能夠在保證控制系統頻域指標的同時,提高隔離水平。但是該方法由于受到控制系統設計的約束,對于隔離度水平的提高受到一定的限制。

圖16 彈簧力矩隔離度Fig.16 Disturbance rejection rate caused by spring torque

圖17 阻尼力矩隔離度Fig.17 Disturbance rejection rate caused by damping moment

6 結 論

為了改進導引頭跟蹤度特性和時域特性,通過對帶導引頭內外回路帶寬與導引頭時域性能分析,提出了一種保證幅值裕度和相位裕度約束條件下進行內外回路優化設計的方法,穩定回路以導引頭隔離度指標最優為目標函數,跟蹤回路以導引頭時域響應最優為目標函數,并對設計結果進行了仿真驗證,得到結論如下:

(1) 導引頭隔離度與穩定回路增益有重要關系,在保證穩定回路穩定裕度的條件下,提高穩定回路增益可以提高導引頭隔離度;

(2) 基于隔離度特性的導引頭控制系統優化設計,既保證了導引頭幅值裕度和相位裕度要求,也使系統具有較好的魯棒性;

(3) 通過內外回路優化設計,提高了導引頭隔離度水平,導引頭也具有較好的時域特性。但由于控制系統設計約束,導引頭隔離度水平的提高受到限制。

以上結論表明,基于隔離度特性的導引頭控制系統優化設計對平臺導引頭控制系統設計具有重要參考作用。

[1] 鄢琴濤,李娜,魯天宇,等.導引頭隔離度機理及其寄生回路頻域影響分析[J].彈箭與制導學報, 2016, 36(2): 43-51.

YAN Q T, LI N, LU T Y, et al. Research on disturbance rejection rate mechanism of seeker and frequency domain analysis for parasitic loop[J]. Journal of Projectiles Rockets Missiles and Guidance, 2016, 36(2): 43-51.

[2] 李富貴,夏群利,崔曉曦,等.導引頭隔離度寄生回路對視線角速度提取的影響[J].宇航學報, 2013, 34(8): 1072-1077.

LI F G, XIA Q L, CUI X X, et al. Effect of seeker disturbance rejection rate parasitic loop on line of sight rate extraction[J]. Journal of Astronautics, 2013, 34(8): 1072-1077.

[3] KWON Y S, HWANG H Y, CHOI Y S. Stabilization loop design on direct drive gimbaled platform with low stiffness and heavy inertia[C]∥Proc.of the IEEE International Conference on Control, Automation and Systems, 2007: 320-325.

[4] 李富貴,夏群利,祁載康.導引頭隔離度寄生回路對最優制導律性能的影響[J].航空學報, 2013, 34(12): 2658-2667.

LI F G, XIA Q L, QI Z K. Effect of seeker disturbance rejection rate parasitic loop on performance of optimal guidance law[J]. Acta Aeronautica et Astronautica Sinica,2013,34(12):2658-2667.

[5] SONG J M, CAI G H, KONG L X, et al. Precision analysis of the semi-strapdown homing guided system[J].Journal of Aerospace Engineering,2014,27(1):151-167.

[6] 崔瑩瑩,夏群力,祁載康.導引頭穩定平臺隔離度模型研究[J].彈箭與制導學報, 2006, 26(1): 22-25.

CUI Y Y, XIA Q L, QI Z K. Seeker platform disturbance rejection mathematical model[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2006, 26(1): 22-25.

[7] 杜運理,夏群利,祁載康.導引頭隔離度相位滯后對寄生回路穩定性影響研究[J].兵工學報,2011,32(1): 28-32.

DU Y L, XIA Q L, QI Z K. Research on effect of seeker disturbance rejection rate with phase lag on stability of parasitical loop[J]. Acta Armamentarii, 2011, 32(1): 28-32.

[8] 宋韜,林德福,王江.平臺導引頭隔離度對導彈制導系統影響[J].哈爾濱工程大學學報, 2013, 34(10): 1234-1241.

SONG T, LIN D F, WANG J. Influence of seeker disturbance rejection rate on missile guidance system[J]. Journal of Harbin Engineering University, 2013, 34(10): 1234-1241.

[9] 宗睿,林德福,王偉,等.基于多模型的捷聯紅外導引頭隔離度在線補償方法[J].系統工程與電子技術, 2017, 39(1):147-155.

ZONG R, LIN D F, WANG W, et al. Multiple mode based on-line compensation for disturbance rejection rate of strapdown infrared seeker[J]. Systems Engineering and Electronics, 2017, 39(1):147-155.

[10] 胡歐磊,王江,黃鵬,等.半捷聯導引頭隔離度影響與STUKF在線補償[J].紅外與激光工程, 2017, 46(3): 158-167.

HU O L, WANG J, HUANG P, et al. Effect of disturbance rejection rate on semi-strapdown seeker and on-line compensation of STUKF[J].Infrared and Laser Engineering, 2017, 46(3): 158-167.

[11] ABHINJT B R N B. Performance analysis of nominal scheme and decoupling loop scheme for RF seeker[C]∥Proc.of the AIAA Guidance, Navigation, and Control Conference and Exhibit, 2002.

[12] 徐嬌,王江,宋韜,等.基于擾動觀測器的導引頭隔離度抑制方法研究[J].兵工學報, 2014, 35(11): 1790-1798.

XU J, WANG J, SONG T, et al. A disturbance observer-based inhibition method for disturbance rejection rate of seeker[J]. Acta Armamentarii, 2014, 35(11): 1790-1798.

[13] SONG T, LIN D F, WANG J. Disturbance observer-based control for missile non-strapdown seeker disturbance rejection[J]. Advances in Mechanical Engineering, 2016, 8(4): 1-15.

[14] YU S, ZHAO Y Z. Simulation study on a friction compensation method for the inertial platform based on the disturbance observer[J]. Proceedings of the Institution of Mechanical Engineers Part G-Journal of Aerospace Engineering, 2008, 222(3): 341-346.

[15] LIN C L, HSIAO Y H. Adaptive feedforward control for disturbance torque rejection in seeker stabilizing loop[J]. IEEE Trans.on Control Systems Technology,2001,9(1): 108-121.

[16] MASTEN K M. Applications of control theory to design of line-of-sight stabilization system[C]∥Proc.of the American Control Conference, 1985:1219-1222.

[17] 李富貴,夏群利,蔡春濤,等.導引頭隔離度對寄生回路穩定性的影響[J].紅外與激光工程, 2013, 42(9): 2341-2347.

LI F G, XIA Q L, CAI C T, et al. Effect of seeker disturbance rejection rate on parasitical loop stability[J]. Infrared and Laser Engineering, 2013, 42(9): 2341-2347.

[18] TOSCANO R. A simple robust PI/PID controller design via numerical optimization approach[J]. Journal of Process Control,2005,15(1):81-88.

[19] CHANG C H, HAN K W. Gain margins and phase margins for control systems with adjustable parameters[J]. Journal of Guidance, 1990, 13(3): 404-408

[20] WANG Y J. Graphical computation of gain and phase margin specifications-oriented robust PID controllers for uncertain system with time-varying delay[J]. Journal of process Control, 2011, 21(4): 475-488.

[21] 歐林林,顧誕英,張衛東.基于幅值裕度和相位裕度的PID參數最優整定方法[J]. 控制理論與應用, 2007, 24(5):837-840.

OU L L, GU D Y, ZHANG W D. Optimal tuning method of PID controller based on gain margin and phase margin[J]. Control Theory & Applications, 2007, 24(5):837-840.