蟻群-魚群混合算法在差異工件批調度中的應用①

呂順風,馬 科

(中國科學技術大學 管理學院,合肥 230026)

1 引言

調度問題是組合優化領域中一類重要的問題,在生產管理、通信等方面有著重要作用.批調度問題是其中的一個重要的分支,而且與經典調度問題不同的是:一臺機器可以同時處理多個工件;批的加工時間等于批中工件的最大完成時間;批的完成時間等于批的開始時間加上批的最大加工時間;批的完成時間等于批中工件的最大完成時間.批調度問題考慮了工件的尺寸和機器的容量,這在實際的活動中經常需要考慮到,例如半導體芯片的預燒、電路測試、港口貨物裝卸、金屬加工等等.這些問題中,工件的尺寸是有差異的,及其加工需要分批進行,批的尺寸不能超過機器的容量.這類問題是經典調度問題在空間上的拓展,也是生產調度領域中一個新的研究方向.

1.1 問題的描述

針對此類問題,首先作如下假設[1]:

(1)有n個待加工的工件{1,2,…,n},工件的加工時間為pj,工件的尺寸為sj;

(2)機器的容量為B,批中工件的總尺寸都小于B,假設沒有工件尺寸大于B的工件;

(3)假設批一旦開始加工,在批加工完成之前,不可以被打斷或者添加新的工件,批k的加工時間為Tk,等于批中最大加工時間的工件;

(4)目標是最大加工時間Cmax最小,其中最大加工時間等于批中最后一個離開機器的工件完成時間,NSBM問題的制造跨度為所有批的加工時間總和.

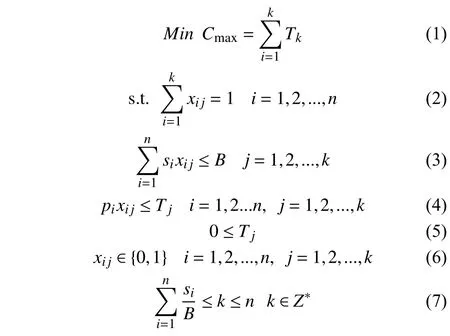
其中,k是分批的批數,xij是0–1變量,式(1)表示優化的目標是制造跨度;式(2)限定每個工件只能分到一個批次中;式(3)表示機器容量約束;式(4)表示批加工時間;式(5)、式(6)和式(7)是基本約束.

Uzsoy首先提出了該類問題的單機器模型,即工件尺寸不同的單機批調度問題(single batch-processing machine with non-identical job sizes,NSBM),證明了當所有工件加工時間相同時,問題等價于容量為B物品尺寸為si的裝箱問題.由于裝箱問題是強NP難的,所以問題也是強NP難的[2].

2 蟻群算法和魚群算法

由于在構建差異工件(即工件有尺寸差異)單機批調度問題的解時,批的加工時間是不確定的,從而不能類似于經典調度問題的蟻群算法,把批加工時間的倒數作為蟻群算法中的啟發式信息.針對這一問題,我們引入批的利用率和批的負載均衡率作為蟻群算法中的啟發式信息,提出了JACO (ant colony optimization based a job sequence)和BACO (ant colony optimization based a batch sequence)兩種蟻群優化算法[5].

2.1 啟發式信息

在一組給定的批次下,當批的總剩余空間越小,方案越佳.此外,批的加工時間等于批中加工時間的最大值,如果在加工完之前,有的工件已經加工完畢卻沒有辦法交付使用,那么這段浪費掉的時間我們稱之為冗余時間.很顯然,對于白白浪費掉的時間,冗余時間越小的方案往往是最優的方案.

批的利用率為批的加工尺寸所占機器容量的比例,公式為:

批的負載率為批中加工時間的變異系數與1的差值,公式為:

Wk為加工時間的平均值,σk表示批加工時間的方差,批的負載率越大,表示批中加工時間分布越均勻,加工方案越好[6].

2.2 算法的描述

2.2.1 JACO蟻群算法

在本文中,我們采用JACO蟻群算法算法,直接考慮工件序列,以方便算法的比較.具體描述如下[7]:

(1)信息素的定義:τij表示工件j排列在工件i之后的信息素濃度,分批的規則采用BF (Best Fit)規則.

(2)啟發式信息:利用BF規則進行分批,實際上就是利用批利用率最大這個啟發式信息,在生成工件序列后,利用BF規則進行分批,工件中間隔較小的工件被分在同一批中概率較大.為方便計算,定義工件j排列在工件i之后的啟發式信息為:

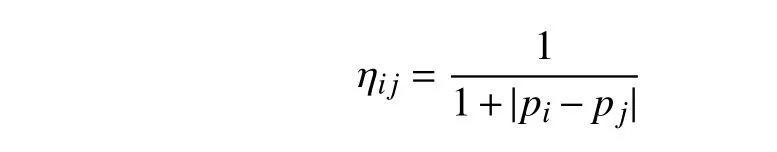
(3)狀態轉移概率公式記為alloweda={j|工件j未被a訪問到},螞蟻a當前位置工件i,那么它的狀態轉移選擇下一個工件概率為[8]:

2.2.2 魚群算法

(1)覓食行為(prey)

覓食行為的行為選擇為:

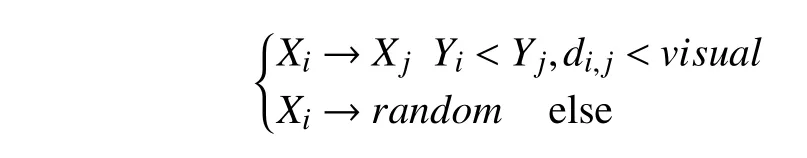
(2)聚群行為(swarm)

聚群行為的行為選擇為:

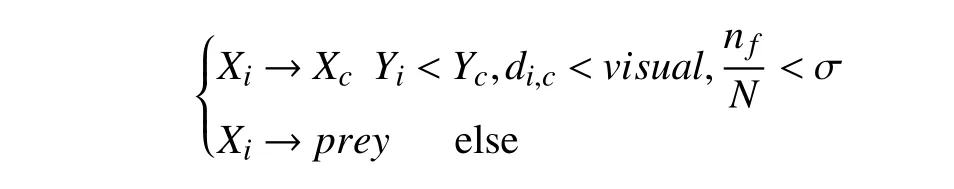
Xc表示領域內伙伴的中心位置.

(3)追尾行為(follow)

追尾行為的行為選擇:

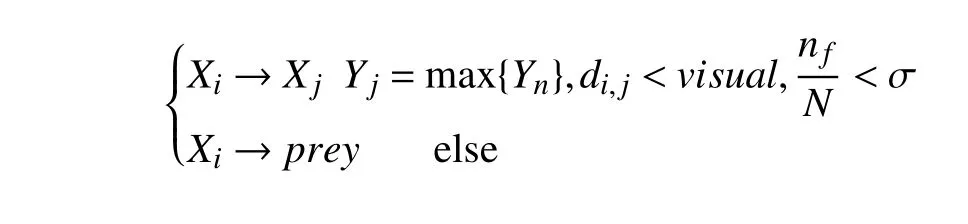
3 混合算法

3.1 蟻群算法和魚群算法的優化機理

蟻群算法和魚群算法雖然都屬于群體優化算法,但是算法中的個體并沒有表現出智能性,個體的行為簡單,只具有基礎的判斷能力,無法智能的遵循相應行為規則,但是當它們形成一個群體的時候,整個群體會表現出一定的智能性.這兩種算法的個體規律有一定的相似性,人工魚群算法初期,人工魚的覓食行為是隨機的,這和蟻群算法是相似的;人工魚群算法后期,人工魚的聚集是由伙伴中心的最優狀態決定的,這與蟻群算法中信息素濃度和啟發式信息大小有著相同的作用.而人工魚的數量越多,就越容易尋找局部最優值,這將有更多的人工魚游到該位置,這相當于蟻群算法信息素濃度增加,類似于螞蟻群算法中信息素正反饋的過程.

和蟻群算法不同的是,人工魚前進的方向是由當前狀態最優的情況決定的,并且在某些條件下會受到擁擠度的限制.如果該地區人工與數量過多,超過擁擠度的約束,即使該地區有很高的價值,人工魚也不會聚集.而在蟻群算法中,信息素關聯著蟻群個體之間的聯系,并且和啟發式信息一起共同指導個體行為,最終所有的螞蟻都會聚集到同一條最佳路徑上來[11].

兩種算法搜索的方式不同,從而個體的運動方式也各不相同,這種差異也是由個體運動的目的不同造成的.啟發式信息在兩種算法的優化中起到了作用,因為個體的目的都是盡快尋找食物.但是擁擠程度并完全不適用于蟻群算法,因為蟻群尋找到食物后會搬回巢穴,而魚群在尋找到食物后會直接吃掉,并不會存儲,而過多的人工魚會導致其它人工魚到這里之前,食物已經被吃光,所以擁擠度對算法的全局性起著關鍵的作用.螞蟻在尋找到食物并且搬回的過程中,如果發現了更高效的路徑,則會轉移到其他路徑上去,在選擇最短路徑上,螞蟻的數量并不受到擁擠度的限制,選擇的螞蟻越多,對結果越好,但是如果這條路徑并非最優選擇,算法可能會被局限在局部最優解中.

因此,兩種算法之間的核心區別是擁擠程度在優化過程中起著指導作用.換句話說,魚群算法類似于于在蟻群算法中引入擁擠度的概念,并且算法優化過程中的擁擠程度總是有著重要作用.擁擠程度的引入可以避免蟻群算法早期,螞蟻過早地聚集到信息素高的路徑上來,避免算法的早熟,提高算法的全局優化能力.算法后期,擁擠度的作用便會從正作用慢慢轉向副作用,對算法的收斂速度產生影響.換句話說,在早期優化中的擁擠程度可以提高算法的優越性能,但是在后期優化中對性能會有一定的負面影響.如何正確使用擁擠度這個因素,是保證算法高效,準確的關鍵[12].

3.2 先魚群再蟻群的混合算法

為了保證較優的可行解,產生初始信息素分布,防止解過早集中到信息素較高的路徑上來,首先使用魚群算法保證求解的寬度,并設置更新迭代率,當算法的更新率少于設定值時,轉入蟻群算法;轉入蟻群算法后,更新信息素,迭代尋找較優解,當結果不再變化時,再次轉入魚群算法,并且調整更新率[13].算法步驟如下:

Step 1.初始化模型和子空間.

Step 2.設置AFSA的最大最小迭代次數Imax,Imin,更新率Rratio和擁擠度.生成m條人工魚,視野長度Vd,擁擠度δ和移動步長Dstep,產生初始人工魚群F(0).

Step 3.每條人工魚進行一次迭代,迭代過程中分別執行覓食,聚群,追尾三種行為,迭代結束后,將結果與公告板相比較,更新最優值.

Step 4.在迭代次數的范圍內,將此次的迭代結果和上一次結果相比較,計算更新率R.如果R＜Rratio,說明優化效果降低,轉入Step 5,如果R＞Rratio,說明魚群算法依然優化效果良好,轉入Step 3.

Step 5.根據魚群算法的迭代結果,生成m只螞蟻,初始化信息素τi,j(0).

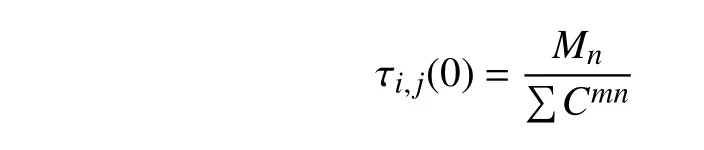
其中,M代表算法中螞蟻的總數量,n是工件數目,∑Cmn表示總完工時間.

Step 6.m只螞蟻隨機放入工件上,根據每條路徑上的信息素濃度,計算狀態轉移概率并且由位置i轉移到位置j,多次迭代后,得到最優結果.

Step 7.判斷算法是否達到最大迭代次數后者滿足輸出條件,若滿足,輸出結果;若不滿足,以蟻群算法的結果為新的人工魚群F(1),并且調整擁擠度閾值和更新率Rratio,轉入Step 3.

3.3 直接嵌入擁擠度的蟻群算法

將擁擠度直接嵌入蟻群算法的迭代過程中,在螞蟻選擇每條路徑時,首先判斷路徑上的擁擠度,如果擁度小于閾值,則繼續選擇該路徑,如果擁擠度大于閾值,則隨機選擇可行的其它路徑.蟻群算法路徑上的擁擠度為:

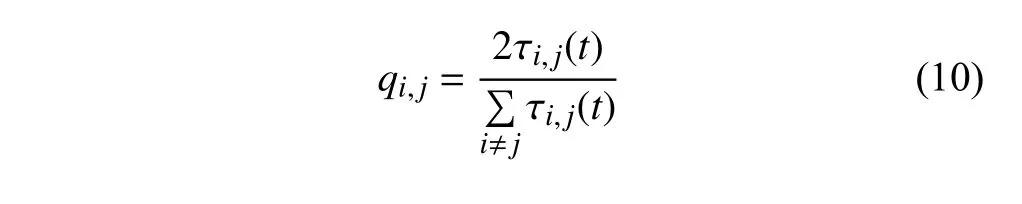
算法步驟如下:

Step 1.初始化時刻t、信息素、擁擠度閾值δt和迭代次數限制Ir.

Step 2.m只螞蟻隨機放入工件上,每只螞蟻根據信息素選擇路徑,狀態轉移概率表示t時刻螞蟻由位置i轉移到位置j的概率,如公式(8).

Step 3.每當螞蟻選擇一條路徑,通過公式(10)計算路徑的擁擠度表示路徑過于擁擠,螞蟻從可行領域內隨機選擇其它路徑;如果表示路徑不太擁擠,螞蟻從i轉移到j.

Step 4.利用BF分批規則對工件序列分批,計算目標函數值;更新信息素τij,如公式(9),和擁擠度閾值δt:

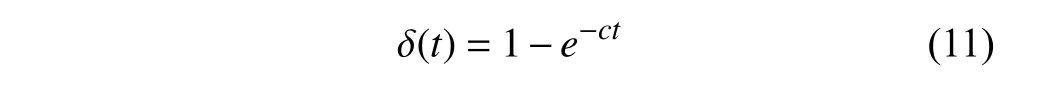
其中,c為閾值變化系數.

Step 5.重復Step 2、3和4,直到所有螞蟻都選擇一條路徑或者達到最大迭代次數.

兩種算法的流程圖如圖1所示.

4 仿真實驗與分析

4.1 實驗設計

為了驗證本文提出的算法有效性,本文的實驗需要兼顧三個方面要素:工件尺寸的變化,工件數的變化,工件加工時間的變化.如表1所示,工件尺寸的大小和加工時間我們采用離散型隨機分布的方式,隨機決定工件尺寸的大小;工件數量方面,我們通過數量遞增的對比結果來對比算法的有效性;算法的有效性我們考慮算法的加工時間和批利用率、負載率的均值.

各個參數的設置為:螞蟻數量m為20、Q=100、τi,j=1/n、ρ=0.5、α=1、β=1.

4.2 實驗結果與分析

加工時間和工件數都是離散的,為了保證實驗的有效性,我們根據工件的數量分為三類,分別對結果加以對比,分別如表2和表3所示.

在表2,表3中可以看出,在算法尋優的過程中,蟻群算法的性能要優于魚群算法,但是蟻群算法本身的早熟性,導致尋優結果局部最優,但是將蟻群算法和魚群算法相結合,利用魚群算法中擁擠度因子,并與蟻群算法相結合,可以有效地避免早熟,并且對于尋找最優解,減少尋優時間有著一定的幫助.通過混合算法3.1和3.2的比較,混合算法3.2對于工件數量較小,迭代次數較少的問題有較高效率.而混合算法3.1對于工件數量較多,迭代次數較多的算法有較高的性能.

圖1 兩種算法流程圖

表1 實驗中的參數設置

5 總結

本文針對差異工件批調度問題,并考慮到蟻群算法的早熟性問題,將魚群算法與之相結合,利用魚群算法中魚群防止過度聚集,擁擠度限制的方法,避開蟻群算法在尋優前期早熟死循環.對于算法結果,本文通過負載率和利用率均值的相比較來判斷算法結果的優劣,迭代次數的比較來對比算法效率.通過對比的結果發現,混合算法前期可以有效避免早熟,而且在算法后期又可以加快收斂,從而使尋優個體能夠加快尋找到滿意解.

但是對于混合算法中,混合算法3.1的更新率、擁擠的閾值,以及混合算法3.2中迭代次數限制,都需要人為確定,但是針對不同情況下,不同的值對結果有著不同的影響,那么工件數量、工件尺寸的分布、工件的加工時間和機器的尺寸和這些值的關系還需要進一步的探究.

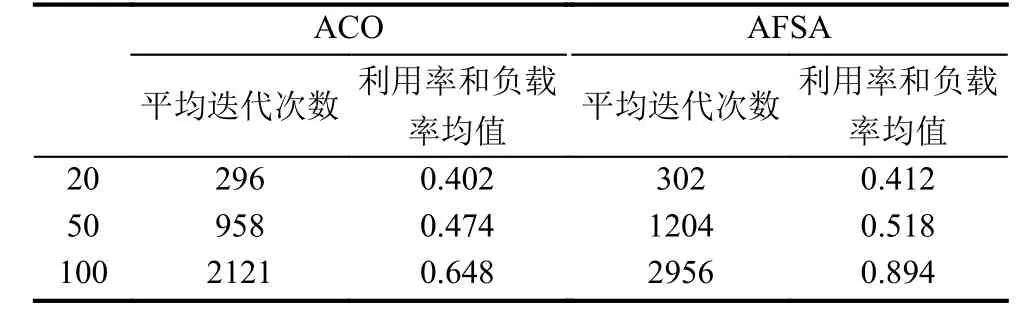
表2 ACO和AFSA算法對比

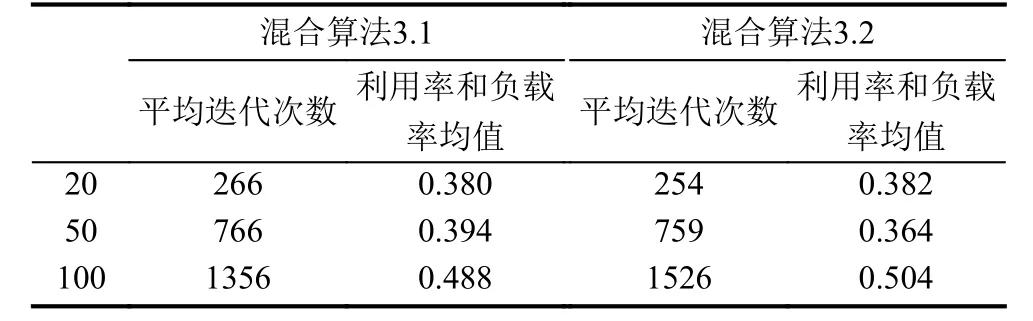
表3 混合算法3.1和3.2對比

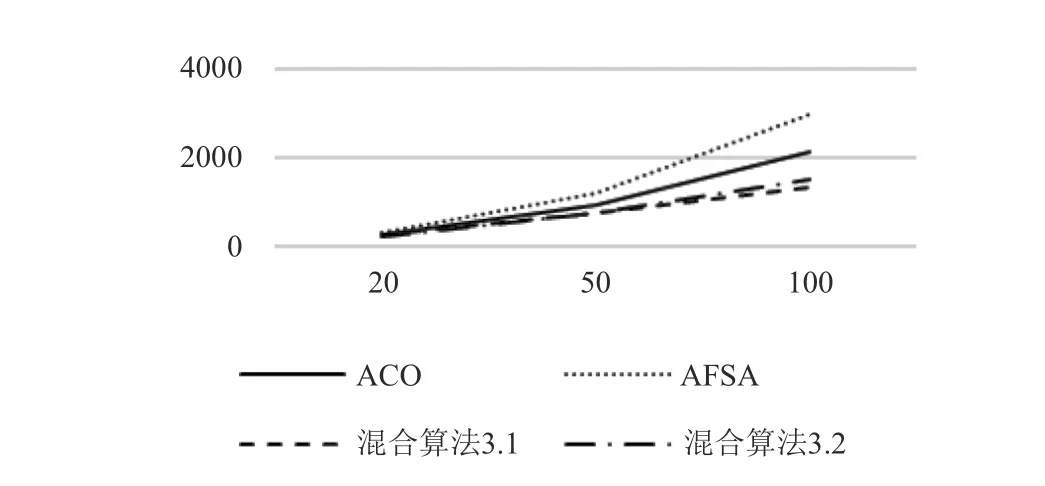
圖2 算法迭代次數對比

圖3 利用率負載率均值對比

1 王栓獅,陳華平,程八一,等.一種差異工件單機批調度問題的蟻群優化算法.管理科學學報,2009,12(6):72–82.

2 Ghazvini FJ,Dupont L.Minimizing mean flow times criteria on a single batch processing machine with non-identical jobs sizes.International Journal of Production Economics,1998,55(3):273–280.[doi:10.1016/S0925-5273(98)00067-X]

3 Melouk S,Damodaran P,Chang PY.Minimizing makespan for single machine batch processing with non-identical job sizes using simulated annealing.International Journal of Production Economics,2004,87(2):141–147.[doi:10.1016/S0925-5273(03)00092-6]

4 Damodaran P,Manjeshwar PK,Srihari K.Minimizing makespan on a batch-processing machine with non-identical job sizes using genetic algorithms.International Journal of Production Economics,2006,103(2):882–891.[doi:10.1016/j.ijpe.2006.02.010]

5 王笑蓉,吳鐵軍.Flowshop問題的蟻群優化調度方法.系統工程理論與實踐,2003,23(5):65–71.

6 姜樺,李莉,喬非,等.蟻群算法在生產調度中的應用.計算機工程,2005,31(5):76–78,101.

7 王常青,操云甫,戴國忠.用雙向收斂蟻群算法解作業車間調度問題.計算機集成制造系統,2004,10(7):820–824.

8 盧輝斌,范慶輝,賈興偉.一種改進的自適應蟻群算法.計算機工程與設計,2005,26(11):3065–3066.[doi:10.3969/j.issn.1000-7024.2005.11.064]

9 李曉磊,邵之江,錢積新.一種基于動物自治體的尋優模式:魚群算法.系統工程理論與實踐,2002,22(11):32–38.[doi:10.3321/j.issn:1000-6788.2002.11.007]

10 李曉磊,路飛,田國會,等.組合優化問題的人工魚群算法應用.山東大學學報(工學版),2004,34(5):64–67.

11 侯景偉,孔云峰,孫九林.基于多目標魚群-蟻群算法的水資源優化配置.資源科學,2011,33(12):2255–2261.

12 王聯國,洪毅,趙付青,等.一種改進的人工魚群算法.計算機工程,2008,34(19):192–194.[doi:10.3969/j.issn.1000-3428.2008.19.065]

13 修春波,張雨虹.基于蟻群與魚群的混合優化算法.計算機工程,2008,34(14):206–207,218.[doi:10.3969/j.issn.1000-3428.2008.14.073]