ANFIS與模糊聚類—ESN的光伏發電功率預測模型比較

王大虎+賈倩+林紅陽

摘要：光伏電站的發電功率高度依賴于不同的天氣條件，其變化無規律可循，從而給電網管理帶來挑戰。因此，對光伏發電功率進行預測研究，以確保電網安全、穩定運行。首先，按季節和天氣類型劃分歷史發電數據，經數據分析后，將溫度與歷史發電功率作為輸入，構建了ANFIS與模糊聚類-ESN兩個光伏發電功率預測模型。利用Matlab模糊邏輯工具箱構建ANFIS模型，而對于模糊聚類-ESN模型的構建，先采用模糊聚類處理輸入數據，再利用ESN進行訓練與預測。通過對兩個預測結果的比較，模糊聚類-ESN模型的預測精度高于ANFIS模型。

關鍵詞：自適應神經模糊推理系統；模糊聚類；回聲狀態網絡；光伏發電功率預測

DOIDOI：10.11907/rjdk.172090

中圖分類號：TP319

文獻標識碼：A文章編號文章編號：1672-7800（2018）001-0157-05

Abstract：Power generation output of a PV plant is highly dependent on different weather conditions， but its changes are irregular， which pose a challenge to grid management. For this， scholars to predict the photovoltaic power generation to ensure that the grid safe and stable operation. In this paper， the historical power generation data is divided directly by season and weather type. After the data analysis， take the temperature and historical power generation as input. Two photovoltaic power generation models， the adaptive neural fuzzy reasoning system （ANFIS） and the fuzzy clustering-ESN， are constructed. ANFIS model is constructed by Matlab fuzzy logic toolbox. The construction of fuzzy clustering-ESN model is used to process the input data with fuzzy clustering， and then ESN is used to train and predict. Comparing the two prediction results， the fuzzy clustering-ESN model has higher prediction accuracy than ANFIS model.

Key Words：adaptive neuro-fuzzy inference system（ANFIS）； fuzzy clustering； echo state network（ESN）； photo-voltaic power generation prediction

0引言

環境污染與資源短缺帶來的壓力，迫使全球范圍內進入可持續發展時代，環境友好型的可再生能源利用受到各國政府的高度重視。光伏發電作為繼水力發電、風力發電等可再生能源的一種形式，其發展對經濟、社會和環境都具有積極影響。目前，國內外已經建立了大量大規模的光伏發電系統，但因光伏發電系統的輸出易受太陽輻射強度和天氣等不確定因素影響，使其具有隨機性和間接性，導致光伏發電系統無法穩定運行[1-3]。近年來，隨著兆瓦級光伏發電系統并網運行的增加，電網的安全、穩定運行更加受到重視。因此，對光伏發電系統輸出功率的隨機性進行準確預測，進而對電網調度進行合理安排顯得尤為重要。

人工神經網絡（Artificial Neural Networks，ANN）已被廣泛應用于光伏發電功率預測中。回聲狀態網絡是基于儲蓄池的計算網絡，是ANN的一種類型，在光伏發電功率預測方面也取得了一定成果[4-6]。光伏發電功率數據是不確定、無規律可循的，為得到更準確的預測結果，需在預測前對數據進行處理，使其具有一定規律。文獻[5]、[7-9]通過經驗模態分解（EMD）方法對歷史數據進行處理，得到不同尺度的模態分量和趨勢分量數據后，對數據建立預測模型；文獻[6]、[10-12]通過聚類算法將光伏發電功率歷史數據劃分為若干類，再通過分類識別找出與預測日最相似的一類歷史數據集進行預測。利用以上的數據處理方法都得到了較準確的功率預測值。ANFIS是神經網絡自適應能力和模糊系統推理能力的集成，可從數據集中開發出模糊推理系統，再通過神經網絡建立相應模型。采用ANFIS對光伏發電功率進行預測是一個合適的方法[13-14]。

本文將構建ANFIS和聚類-ESN兩個預測模型，通過分析歷史光伏發電功率的影響因素，可直接將數據按季節和天氣類型進行劃分，最終將溫度作為變量與歷史數據一同輸入。可直接利用Matlab模糊邏輯工具箱實現ANFIS預測模型，而對于聚類-ESN預測模型，采用模糊聚類算法處理輸入數據后，利用回聲狀態網絡對數據進行訓練與預測。通過比較兩個模型的預測值，選擇出預測精度更高的預測模型。

1光伏發電功率輸入變量確定

光伏發電的核心是通過光伏電池組件，將光能直接轉換成電能，其輸出功率為：

其中，Ps為單位面積的光伏系統輸出功率，η為光伏陣列的轉換效率，S為光伏陣列的總面積，Ir為光伏陣列接收的太陽輻射強度，Tc為光伏組件板溫度。endprint

在某光伏電站中光伏陣列的轉換效率、總面積等是確定的，由上式可知，影響光伏發電功率的主要變量因素為太陽輻射強度和光伏組件溫度，其中光伏組件溫度主要受環境溫度影響。

1.1光伏發電功率太陽輻射強度影響

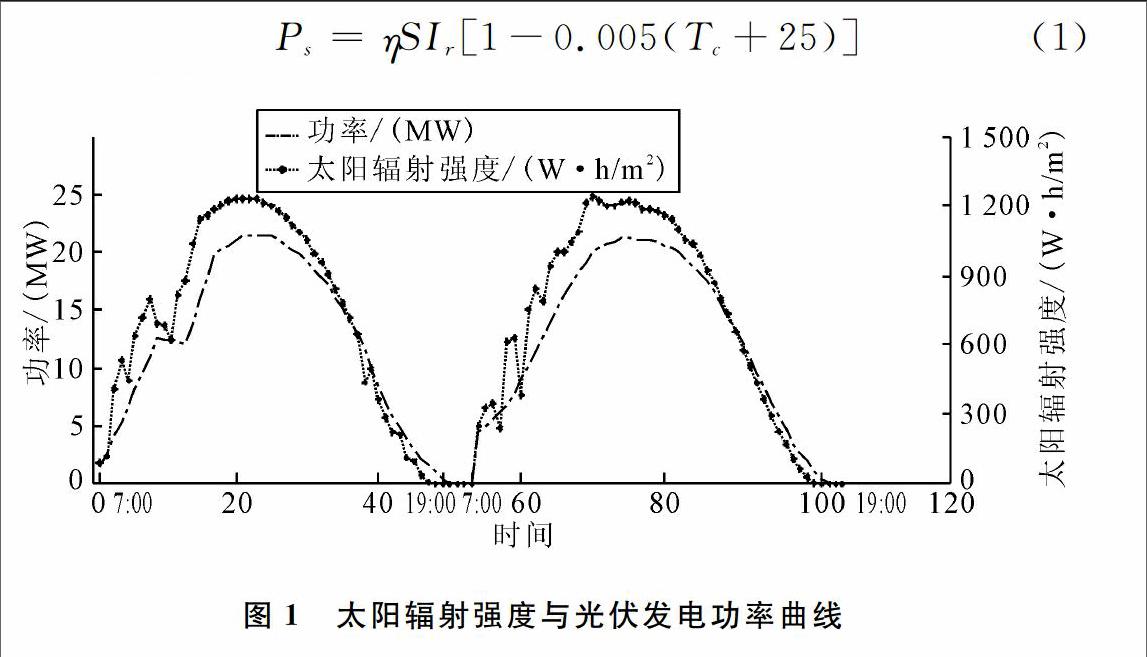
太陽輻射強度的變化對光伏發電功率的影響十分顯著，如圖1所示。

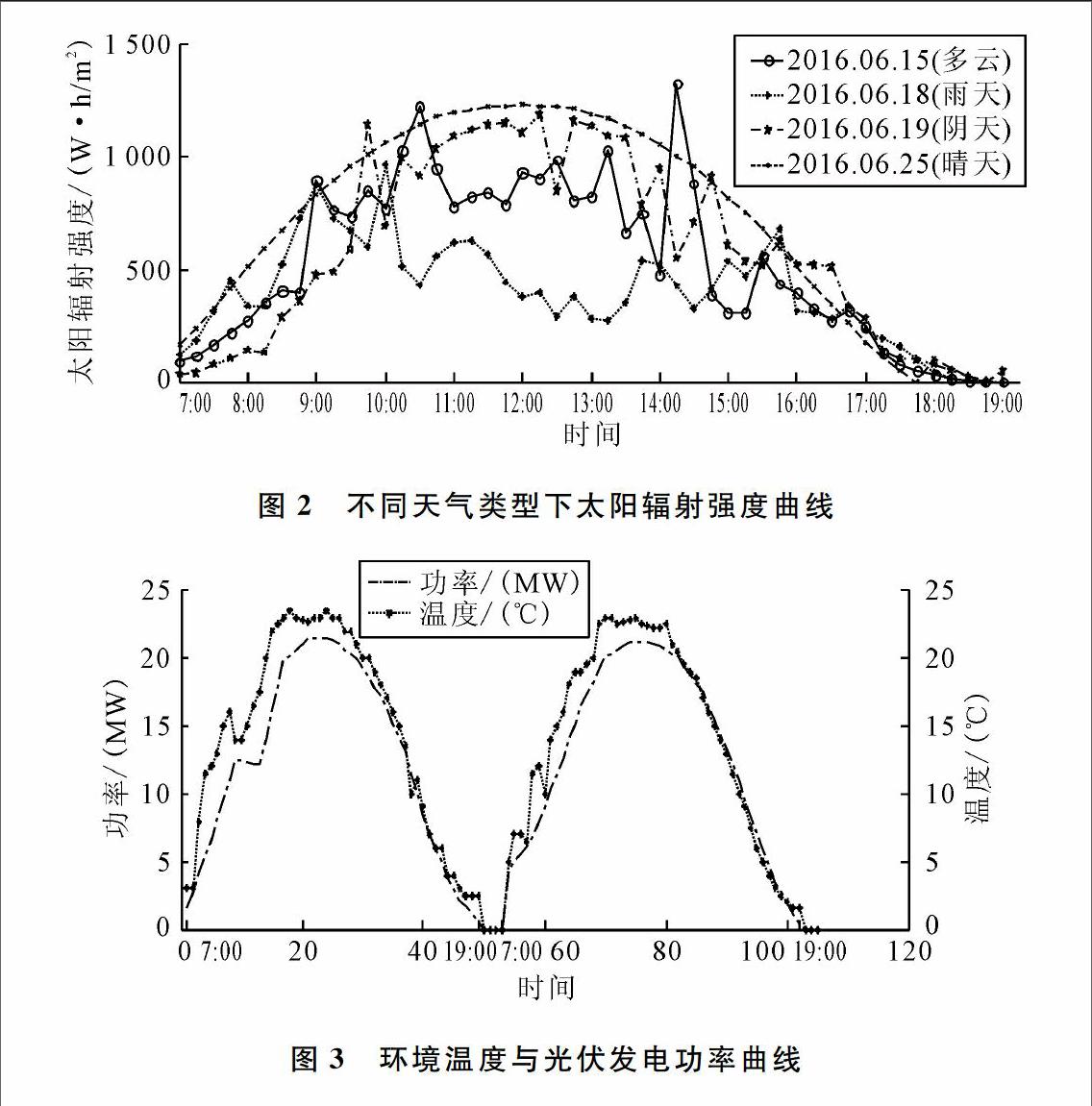
由圖1可知，光伏發電功率隨著太陽輻射強度的增加而增大，呈現對應關系。因此，需將太陽輻射強度作為光伏發電功率的一個輸入變量。但因我國輻照觀測點較少，獲取輻射強度數據較為困難，為解決這一難題，考慮天氣類型與太陽輻射強度的相應關系，文獻[15]、[16]采用天氣類型代替太陽輻射強度。圖2為不同天氣類型下太陽輻射強度的相關曲線。

由圖2得出，不同天氣類型下，太陽輻射強度差異較大。天氣類型為晴天時，太陽輻射強度曲線波動平穩，有明顯規律；在其它天氣類型時，太陽輻射強度曲線波動較大，無明確規律。因此，可將歷史數據按天氣類型進行篩選作為輸入變量，以取代太陽輻射強度的變化。

1.2光伏發電功率溫度影響

環境溫度的變化對光伏發電功率也存在影響，如圖3所示。

由圖可知，當環境溫度在一定范圍內變化時，光伏發電功率隨著環境溫度發生相應變化，但當環境溫度達到某一臨界點時，溫度繼續升高，光伏發電功率反而下降。這是因為環境溫度會直接影響光伏陣列板的溫度，環境溫度越高，光伏陣列板的溫度也越高，導致發電性能下降[17]。

綜合以上影響光伏發電功率的因素，將環境溫度和天氣類型作為預測光伏發電功率的變量，又因天氣類型可通過天氣預報得出，在變量輸入前可直接對其分類，則本文的預測輸入變量為環境溫度，其包括最高溫度Tmax、最低溫度Tmin與平均溫度Tmean。

2ANFIS預測模型

2.1自適應模糊推理系統

自適應網絡模糊推理系統（ANFIS）是將神經網絡的學習機制和模糊系統的推理能力相結合的自適應系統，由Sugeno[18]最早提出。ANFIS利用神經網絡的學習能力，從輸入輸出數據集中開發模糊推理系統。學習模糊系統的隸屬函數參數，可準確跟蹤給定的輸入和輸出集合[19]。為確定模糊系統的最優隸屬函數形狀，ANFIS建立了一個模糊推理系統（Fuzzy Inference System，FIS），其隸屬函數參數通過訓練數據在已建立的模糊規則上不斷學習、調整，構造出最佳的輸入—輸出映射[20-21]。

2.2ANFIS預測模型

本文以福建某30MW光伏電站為例，以夏季一天中7：00～19：00每1小時的時間間隔溫度為輸入變量，包括最高溫度Tmax、最低溫度Tmin與平均溫度Tmean，以預測發電功率P。本節使用Matlab模糊邏輯工具箱實現ANFIS系統，基于其自學習過程，使用混合學習算法調整并獲得ANFIS模塊的最優隸屬函數。算法包括最小二乘法與梯度下降的反向傳播法的組合。表1給出了通過訓練ANFIS獲得的輸入/輸出變量范圍、隸屬函數類型和隸屬函數。表2為基于規則的模糊推理系統，含有8個規則，3個輸入變量的2個隸屬函數和1個輸出變量的8個隸屬函數，輸出隸屬函數被命名為P1-P8。

圖4給出了本節對應的ANFIS結構圖。由圖可知，ANFIS結構分為5層，且同一層網絡的每個節點具有相似功能，用O1，i表示第一層第i個節點的輸出，依此類推。該模糊推理系統有3個輸入x、y、z分別表示Tmax、Tmin、Tmean，以及一個輸出f。

第一層：對輸入參數進行模糊化，確定對應模糊集的隸屬度：

其中，i由{m，n，l}的相應組合構成，且i=1，2，…，8；Am、Bn和Cl為模糊集，文中表示的模糊意義為溫度的“低”和“高”；μAm（x）、μBn（y）和μCl（z）為模糊集的隸屬函數，表示x、y、z屬于模糊集Am、Bn、Cl的程度。隸屬度函數包括：鐘形函數、三角形函數、梯形函數及高斯型函數等。

3模糊聚類-ESN預測模型

3.1模糊聚類

聚類是根據“最小化類間相似性，最大化類內相似性”原則，將數據集分類成不同類或簇的過程，即由聚類生成的同一簇中的數據具有很大的相似性，而不同簇間的對象有很大的相異性。聚類分析是研究樣品或指標分類問題的一種統計分析方法，同時也是數據挖掘的一個重要算法。聚類分析內容非常豐富，模糊聚類法即是其中一種。

模糊聚類指根據研究對象自身屬性構造模糊矩陣，并根據一定隸屬度確定聚類關系，即通過模糊數學方法定量確定樣本間的模糊關系，從而客觀且準確地進行聚類。

通過對光伏發電功率進行分析，將光伏發電功率的歷史數據V和溫度數據T作為輸入樣本，表示如下：

其中，P為發電站輸出功率的實際值，為預測模型得到的預測值，n為預測樣本個數，i為第i個數據點。

圖6顯示了利用ANFIS和模糊聚類-ESN預測模型獲得的連續4天的功率預測結果。表3比較了兩種預測模型的準確性。

由圖6可以看出，不同天氣類型下，ANFIS和模糊聚類-ESN預測模型的預測值相對于實際值的偏差波動大小存在差異。當天氣類型處于平穩波動時（如：晴天），偏差較小；當處于波動較大的天氣類型時（如：陰、雨、多云），偏差也較大。模糊聚類-ESN模型的功率預測曲線更接近實際功率曲線，明顯優于ANFIS預測模型。通過表3的誤差對比可知，本文構建的兩個預測模型中，ANFIS模型MAE和RMSE的預測誤差值約為模糊聚類-ESN模型的兩倍，且模糊聚類-ESN模型與ANFIS模型相比，其預測精度提高了47.46%，即得出模糊聚類-ESN模型相比于ANFIS模型具有更高的預測精度。

5結語

本文構建了ANFIS與模糊聚類-ESN的光伏發電功率預測模型，兩種預測模型均先對輸入數據進行模糊化處理后，傳入各自的訓練網絡中。本文按季節和天氣類型對歷史光伏發電功率數據進行直接劃分，并將溫度與劃分的數據一同作為預測模型的輸入，對網絡進行訓練與預測。最后，將ANFIS的預測結果與聚類-ESN進行比較，得出模糊聚類-ESN預測模型具有更高的預測精度。endprint

參考文獻：

[1]P Y LIM， FARRAH WONG. Photovoltaic power predictions using modified adaptive response rate exponential smoothing method[C]. IEEE International Conference on Sustainable Energy Technologies，2016.

[2]L BIRD， M MILIGAN， D LEW. Integrating variable renewable energy： challenges and solutions[R]. Office of Scientific & Technical Information Technical Reports，2013.

[3]陳亞博，盛戈皞，黎建，等.含光伏和風電的電力系統隨即生產模擬[J].電力系統及其自動化學報，2015，27（5）：1-6.

[4]I JAYAWARDENE， G K VENAYAGAMOORTHY. Comparison of adaptive neuro-fuzzy inference systems and echo state networks for pv power prediction[J]. Procedia Computer Science，2015，53：92-102.

[5]李多，董海鷹，楊麗霞.基于EMD與ELM的光伏電站短期功率預測[J].可再生資源，2016，34（2）：173-177.

[6]李樂，劉天琪.基于近鄰傳播聚類和回聲狀態子網絡的光伏預測[J].電力自動化設備，2016，36（7）：41-46.

[7]高相銘，楊世鳳，潘三博.基于EMD和ABC-SVM的光伏并網系統輸出功率預測研究[J].電力系統與控制，2015，43（21）：86-92.

[8]陽霜，羅滇生，何洪英，等.基于EMD-LSSVM的光伏發電系統功率預測方法研究[J].太陽能學報，2016，37（6）：1387-1395.

[9]徐敏姣，徐青山，袁曉冬.基于改進EMD及Elman算法的短期光伏功率預測研究[J].現代電力，2016，33（3）：8-13.

[10]代倩，段善旭，蔡濤，等.基于天氣類型識別的光伏系統短期無輻照度發電預測模型研究[J].中國電機工程學報，2011，31（34）：28-35.

[11]陳昌松，段善旭，蔡濤，等.基于模糊識別的光伏發電短期預測系統[J].電工技術學報，2011，26（7）：83-89.

[12]于秋玲，許長清，李珊，等.基于模糊聚類和支持向量機的短期光伏功率預測[J].電力系統及其自動化學報，2016，28（12）：115-118.

[13]YUAN-KANG WU， CHAO-RONG CHEN， HASIMAH ABDUL RAHMAN. A novel hybrid model for short-term forecasting in PV power generation[J]. International Journal of Photoenergy，2014（29）：1-9.

[14]鄭凌蔚，劉士榮，毛軍科，等.一種綜合ANFIS和PCA的光伏發電功率預測新方法[J].太陽能學報，2012，33（6）：993-1000.

[15]王守相，王亞旻，劉巖，等.基于經驗模態分解和ELM神經網絡的逐時太陽能輻照量預測[J].電力自動化設備，2014，34（8）：7-12.

[16]李樂，劉天琪.基于近鄰傳播聚類和回聲狀態網絡的光伏預測[J].電力自動化設備，2016，36（7）：41-46.

[17]陳紅兵，陳希琳，王起，等.冷卻肋片對光伏板發電性能的影響研究[J].可再生能源，2015，33（3）：346-350.

[18]SUGENO M， KANG G T. Structure identification of fuzzy model[J]. Fuzzy Sets and System，1988，28（1）：15-33.

[19]JYH-SHING， ROGER JANG. Anfis： adaptive-network-based fuzzy inference system[J].IEEE Transactions on systems， Man and Cybernetics，1993，23：665-685.

[20]I JAYAWARDENE， G K VENAYAGAMOORTHY. Comparison of adaptive neuro-fuzzy inference systems and echo state networks for PV power prediction[J]. Procedia Computer Science，2015，53：92-102.

[21]李鵬程，陳國華，張力，等.基于ANFIS的人因失誤風險嚴重度識別[J].中國安全科學學報，2014，24（1）：72-77.

[22]ALI DEIHIMI， HEMEN SHOWKATI. Application of echo state networks in short-term electric load forecasting[J]. Energy，2012，39（1）：327-340.

[23]張晉雁，陶宏才.回聲狀態網絡研究[J].成都信息工程學院學報，2015，30（6）：546-550.

（責任編輯：黃健）endprint