頁巖氣水平井縫內砂塞分段工藝的增產機理

李德旗 何 封 歐維宇 朱炬輝 李 然 潘 勇

1.中國石油浙江油田公司 2.中國石油川慶鉆探工程公司

0 引言

目前國內外頁巖氣增產改造普遍采用水平井、大規模分段體積壓裂，工藝以橋塞分段結合多簇射孔為主[1-2]。川渝地區頁巖氣儲層因其應力結構復雜、埋深差異大（儲層垂深普遍大于2 300 m，部分大于3 000 m）、天然裂縫及斷層發育、施工壓力高、改造難度相對較大等特殊性，致使以橋塞為主的機械分段工藝在川渝頁巖氣的現場應用中受到不同程度的制約。

根據川渝地區頁巖氣壓裂實際情況，壓裂過程中經常出現套管變形等井下復雜情況，套變點超過50%靠近A點附近，常規機械分段工具無法通過，造成大量水平井段無法得到有效改造。據統計，長寧、威遠區塊因套管變形受影響的壓裂段長約13 700 m，受影響的壓裂段數達到176段。因此，亟須一種無機械封隔、對井眼軌跡和井筒尺寸要求小、可實現無限級分段且整個施工過程保持井筒全通徑的新型分段壓裂工藝，為我國頁巖氣儲層增產改造提供一種新的技術手段。

頁巖水平井縫內砂塞分段壓裂工藝[3]利用高砂濃支撐劑在縫口及近井形成人工砂塞，依靠砂塞的阻流作用實現不同層段的封隔及分段改造。該工藝無須機械橋塞坐封，有效規避橋塞相關作業風險、節約施工成本，最大程度減弱了套管變形對儲層改造帶來的不利影響。筆者針對該工藝在頁巖增產改造中其縫內砂塞的導流能力及工藝參數的控制優化進一步展開理論與實驗研究，并結合現場實踐結果驗證其適應性及有效性。

1 縫內砂塞分段高導流能力

頁巖水平井縫內砂塞分段壓裂工藝與常規電纜分簇射孔橋塞聯作工藝相比，其最大的優點是無須電纜泵送橋塞，整個壓裂施工過程中井筒保持全通徑狀態。該工藝主要利用壓裂施工最后階段的高砂濃度支撐劑在縫口及近井形成人工砂塞，以達到常規機械橋塞封隔分段的目的。縫內砂塞分段的效果好壞關鍵在于砂塞能否滿足在儲層閉合應力條件下的抗壓強度、排液階段能否保持穩定及高導流能力。針對以上問題，選取兩種支撐劑受力模型分別研究了在儲層閉合應力條件下支撐劑砂塞的抗壓強度、返排投產過程中縫內砂塞力學穩定性及基于接觸模型的滲透率。

1.1 閉合應力下縫內砂塞強度分析

支撐劑顆粒在滑溜水的攜帶作用下注入地層，隨著液體流速的降低支撐劑顆粒逐漸在縫內沉積并形成無規則堆積[3]。在沒有任何附加力的條件下，支撐劑顆粒將形成任意堆積，堆積結構較松散，接觸不充分，堆積密度較小[4]。但在實際水力裂縫中，隨著壓裂流體的濾失，裂縫縫寬將逐漸變窄，支撐劑顆粒受到閉合應力的擠壓及流體的攜帶等綜合作用將由最初的任意堆積逐步形成密集堆積。根據葉大年[5]的實驗研究，等大球體在密閉空間中可以形成多種不同接觸關系的密集堆積。為了較全面地分析砂塞的可靠性，分別建立了堆積密度較小的體心立方模型及堆積密度最大的面心立方模型（圖1）。

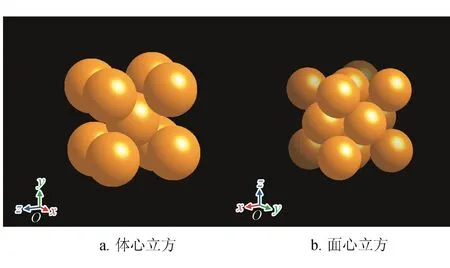
圖1 等大球體體心立方和面心立方示意圖

通常情況下，支撐劑顆粒因其生產過程諸多因素的不可控，必然導致其在尺寸大小、圓球度等方面存在一定差異。在建立支撐劑顆粒的力學模型時將其視為均質等徑、完全彈性的理想球體，因此可將支撐劑顆粒接觸問題轉化為彈性球體間點載荷接觸問題。1881年，Hertz首先用數學彈性力學方法導出表面光滑的彈性球體點載荷接觸問題的計算公式[6]。針對支撐劑密集堆積模型，支撐劑之間滿足點接觸，受力后其接觸表面為圓，符合變形連續條件；整個接觸過程處于彈性階段且服從胡克定律，因此接觸表面上應力應變滿足線性關系；表面接觸壓力所組成的合力等于外加載荷。支撐劑顆粒點接觸如圖2所示。

根據Hertz彈性球體點載荷接觸力學假設可以導出彈性球體接觸表面圓的半徑Ra，兩球在壓應力條件下的接觸形變δ及最大接觸壓應力qmax和壓應力在接觸圓內的分布[7]。式（1）是兩球彈性接觸非線性精細積分式[8]，忽略接觸區域的水平位移則可解得球體接觸表面圓的最大半徑（Ra）、δ、兩球在壓應力條件下位于接觸圓上半徑r處的最大接觸應力（qmax）。

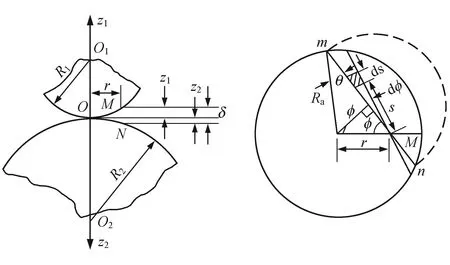
圖2 支撐劑顆粒點接觸關系圖

即

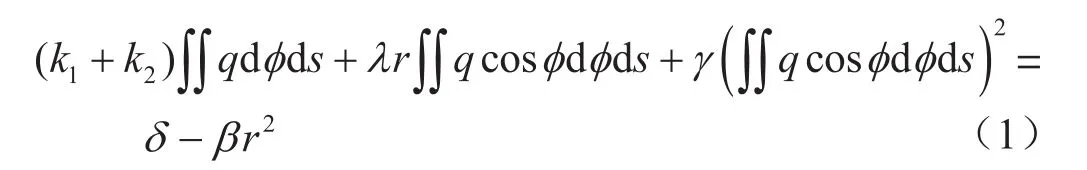
其中

式中q表示兩球在壓應力條件下位于接觸圓上半徑r處的應力，Pa；r表示為接觸圓內任意半徑，m；δ表示兩球在壓應力條件下的接觸形變，m；R1、R2分別表示接觸兩球體的半徑，m；E1、E2分別表示接觸兩球的楊氏模量，Pa；ν1、ν2分別表示接觸兩球體的泊松比，無因次；Ф表示兩球體接觸形變圓上半徑r處的積分角，(°)。

支撐劑顆粒受到的外加載荷主要來自于儲層閉合應力、流體壓力及顆粒自身重力，因支撐劑的視密度僅有2.6～2.8 g/cm3，且顆粒非常細小，因此計算外加載荷時其自重可忽略不計。水力裂縫的閉合應力始終垂直于裂縫壁面（圖3）。設裂縫傾角為θ，則有閉合應力為σ。考慮支撐劑顆粒在裂縫壁面的嵌入作用[9-12]，則有半徑為R的支撐劑球體受到壁面閉合應力與流體壓力pc的最大凈載荷為p：

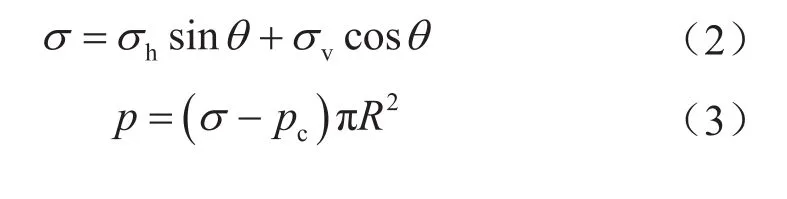
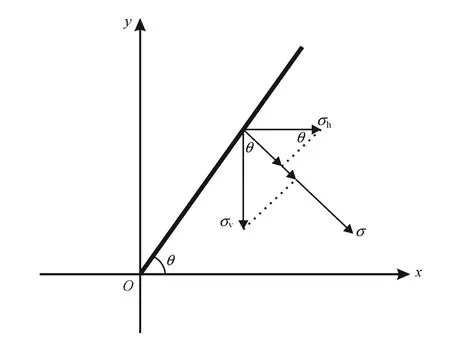
圖3 不同裂縫傾角下閉合應力關系圖

式中σ、σh、σv分別表示裂縫閉合應力、水平及垂向應力，Pa；θ表示裂縫傾角，(°)；p表示支撐劑顆粒受到的凈載荷，N；pc表示流體壓力，Pa；R表示支撐劑顆粒半徑，m。

支撐劑球體之間的接觸滿足彈性球體接觸，因此其破壞判斷準則遵從最大剪應力強度理論，該準則表達式如下：

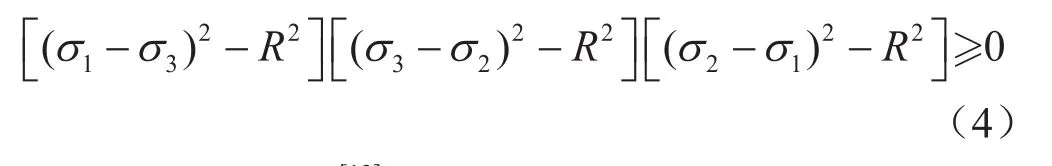
根據陳國輝[13]的研究表明，彈性球體接觸時其最大剪應力為τmax，則有：

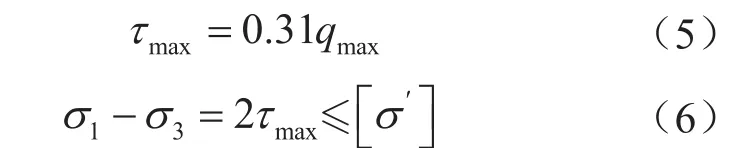
因此，可以應用上述力學模型判斷支撐劑顆粒在屈服強度[σ′]下能否承受儲層外加載荷，能否在該載荷條件下不發生強度破壞。

1.2 流體作用下縫內砂塞穩定性

支撐劑顆粒在水力裂縫中形成前文所述的接觸模型，該類接觸模型除了承受裂縫閉合應力之外，同時也承受施工過程中壓裂流體及返排流體的沖刷作用。縫內砂塞抵抗流體沖刷作用的主要作用力來自于粗糙表面的摩擦阻力。根據庫侖摩擦理論[14]，支撐劑顆粒之間的摩擦阻力與其受到的法向應力正相關，各個模型受到的摩擦阻力如圖4所示。

針對體心立方，因為各個接觸點相互對稱，則有α=45°，所以在圖4所示坐標系條件下最大靜摩擦阻力F1為：

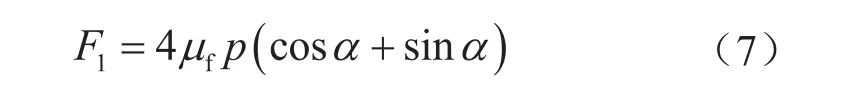
式中F1表示體心立方模型受到的最大靜摩擦阻力，N；μf表示支撐劑顆粒靜摩擦系數，無因次；α表示支撐劑顆粒凈載荷與摩擦面夾角，(°)。

針對面心立方，除了包含體心立方中的8個接觸球外還包含與流體平行的4個接觸球，在圖4所示坐標系條件下有F2為：

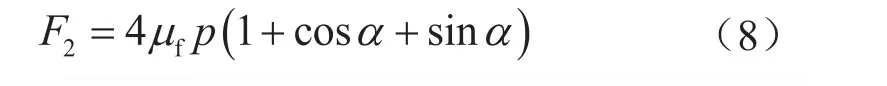
式中F2表示面心立方模型受到的最大靜摩擦阻力，N。

當支撐劑顆粒之間存在流體流動時，流體黏度、氣液比、流速等參數均會影響流體對支撐劑顆粒的沖刷作用。根據流體力學理論，縫內砂塞在流體沖刷作用下主要受到黏滯阻力、壓差阻力等力的影響，單個支撐劑顆粒受到的總沖刷力為FD，則有：

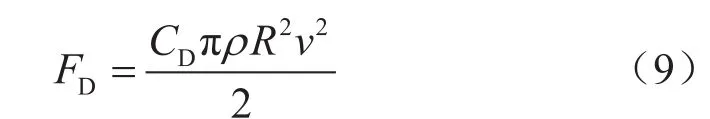
式中FD表示單個支撐劑顆粒受到的總沖刷力，N；CD表示阻力系數，無因次；ρ表示流體密度，kg/m3；v表示流體在支撐劑球體間的流速，m/s。

因此，可以根據沖刷作用力FD與最大靜摩擦阻力的相對大小來判斷縫內支撐劑砂塞能否在注入及返排投產過程中保持穩定。

1.3 基于接觸模型和分形理論砂塞滲透率計算方法

根據體心立方及面心立方中支撐劑顆粒的接觸關系，導出它們在未受閉合應力及流體壓力條件下的最大孔隙度。

在圖5中，為了便于直觀表達各個球體之間的接觸關系，特意將各個球體進行縮小表示，并應用小圓柱體代表球體之間的相切關系。對于體心立方及面心立方模型分別有立方邊長表達式m1、m2為：

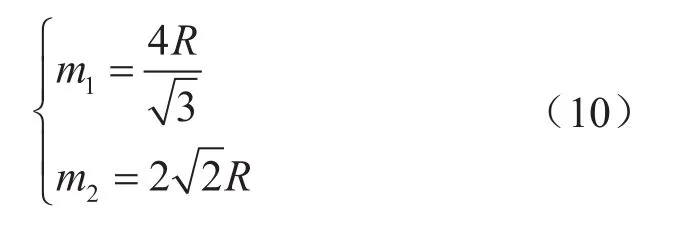
對于體心立方及面心立方模型分別有孔隙度表達式 φ11、φ22為 ：

圖5 等大球體體心立方和面心立方接觸示意圖

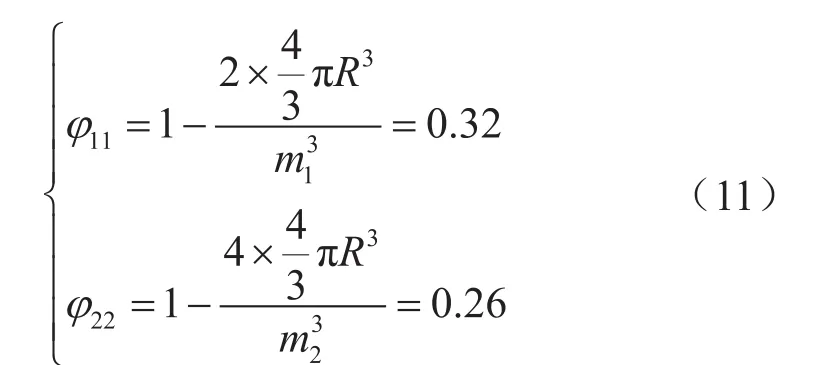
式中R表示為等大球體半徑，m；m1、m2分別表示體心立方及面心立方模型邊長，m；φ11、φ22分別表示體心立方及面心立方模型初始孔隙度，無因次。

儲層條件下縫內砂塞必然受到裂縫壁面的閉合應力以及縫內流體壓力的雙重影響，因此實際砂塞的孔隙度要比根據幾何關系導出的孔隙度低。在裂縫外加載荷作用下，支撐劑顆粒之間相互擠壓，在接觸面上發生形變，最終導致孔隙度進一步縮小（圖6）。

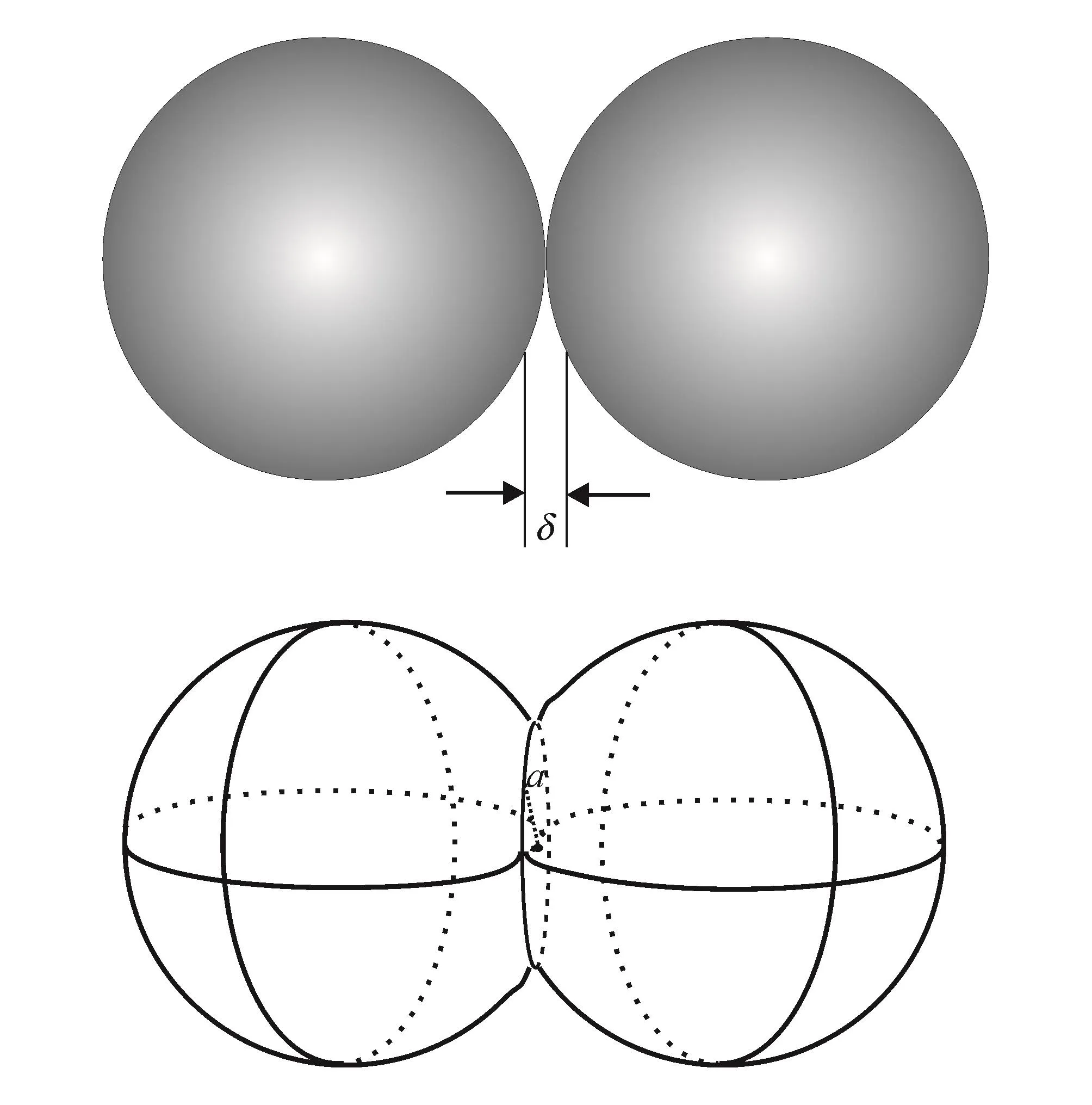
圖6 支撐劑顆粒接觸形變示意圖

應用砂塞強度理論可導出兩種接觸模型因外加載荷作用而分別減少的孔隙度Δφ11、Δφ22。球缺高度為δ/2，球缺截面半徑為Ra，體心立方模型有8個相切接觸，面心立方有36個相切接觸，則有：

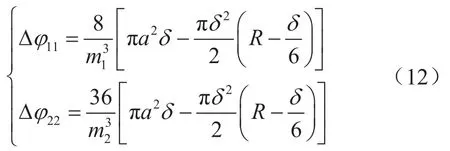
式中Δφ11、Δφ22分別表示體心立方及面心立方模型分別減少的孔隙度，無因次；a表示球缺截面半徑（即球體接觸表面圓的最大半徑），m。

作用于縫內的流體壓力通過流壓變化對支撐劑顆粒孔隙產生影響。流壓增加砂塞孔隙增加，流壓降低砂塞孔隙減小。采用孔隙體積壓縮系數Cp描述流體壓力對砂塞孔隙的影響程度，Cp通過室內實驗測定。尼科拉耶夫斯基 BH等[15]通過研究巖石的壓縮系數Cp，提出了將常壓下室內所測孔隙度轉換為地層條件下的孔隙度的表達式，則有兩種接觸模型在儲層條件下的真實孔隙度為φ1、φ2。即

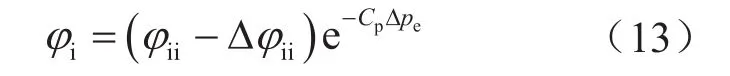
式中Cp表示孔隙體積壓縮系數，MPa－1；Δpe表示流體壓力變化量，MPa；φi、φii、Δφii分別表示體心立方及面心立方模型實際孔隙度、初始孔隙度、因接觸變形減少的孔隙度，無因次。

縫內砂塞具有較好的幾何結構，其孔滲數學關系可用分形理論描述。1975年Mandelbro BB創立的分形理論在很大程度上揭示了油氣藏的宏微觀性質，在多個尺度上表現了它們的分形特征及相互關系。分形多孔介質的滲透率和孔隙度都是多孔介質分維數、分形系數和微觀孔隙結構參數的函數[16-17]，即

其中

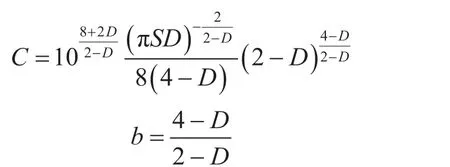
式中C、D分別表示中間變量；K表示砂塞滲透率，D；φ表示孔隙度。

D為分形系數，S為分維數，二者表征了砂塞微觀孔隙/孔喉結構特征，由實驗數據擬合解得。由孔滲關系式可以解得縫內砂塞在儲層條件下的滲透率，結合壓裂裂縫參數最終可以計算出近井地帶的裂縫導流能力。

2 縫內砂塞工程模擬實驗

根據大量頁巖儲層壓裂效果發現，近井縫口處的導流能力對初產及穩產有著重要影響[18-20]。因此，縫內砂塞除了要保證不同層段的有效封隔外，還需在近井地帶維持較高的導流能力。目前，一般是通過提高壓裂階段最后一個攜砂液砂濃度及段塞長度實現近井的高砂濃度封口，以期獲取較高的近井導流能力。梁興等[3]已在現場應用縫內填砂暫堵壓裂技術，該技術縫內填砂階段的砂濃度已遠高于目前常規工藝連續加砂的砂濃度，并取得良好的增產效果。

2.1 砂塞孔隙體積壓縮系數實驗

參照標準SY/T 5815—2016關于孔隙體積壓縮系數的測試規程，應用API標準導流室模擬縫內砂塞，設置孔隙壓力5 MPa，隨后測試不同上覆壓力下的孔隙體積及其變化，最后應用孔隙體積壓縮系數定義計算出不同凈有效壓力下的孔隙體積壓縮系數，凈有效壓力為上覆壓力與孔隙壓力之差值。

實驗結果表明（圖7），孔隙體積壓縮系數隨凈有效壓力增加呈近似指數下降。在整個凈有效壓力測試期間，砂塞孔隙體積壓縮系數在10－2～10－3MPa－1范圍內波動，當凈有效壓力超過30 MPa時孔隙體積壓縮系數隨凈有效壓力的變化趨于平緩，其值近似為 8×10－3MPa－1。

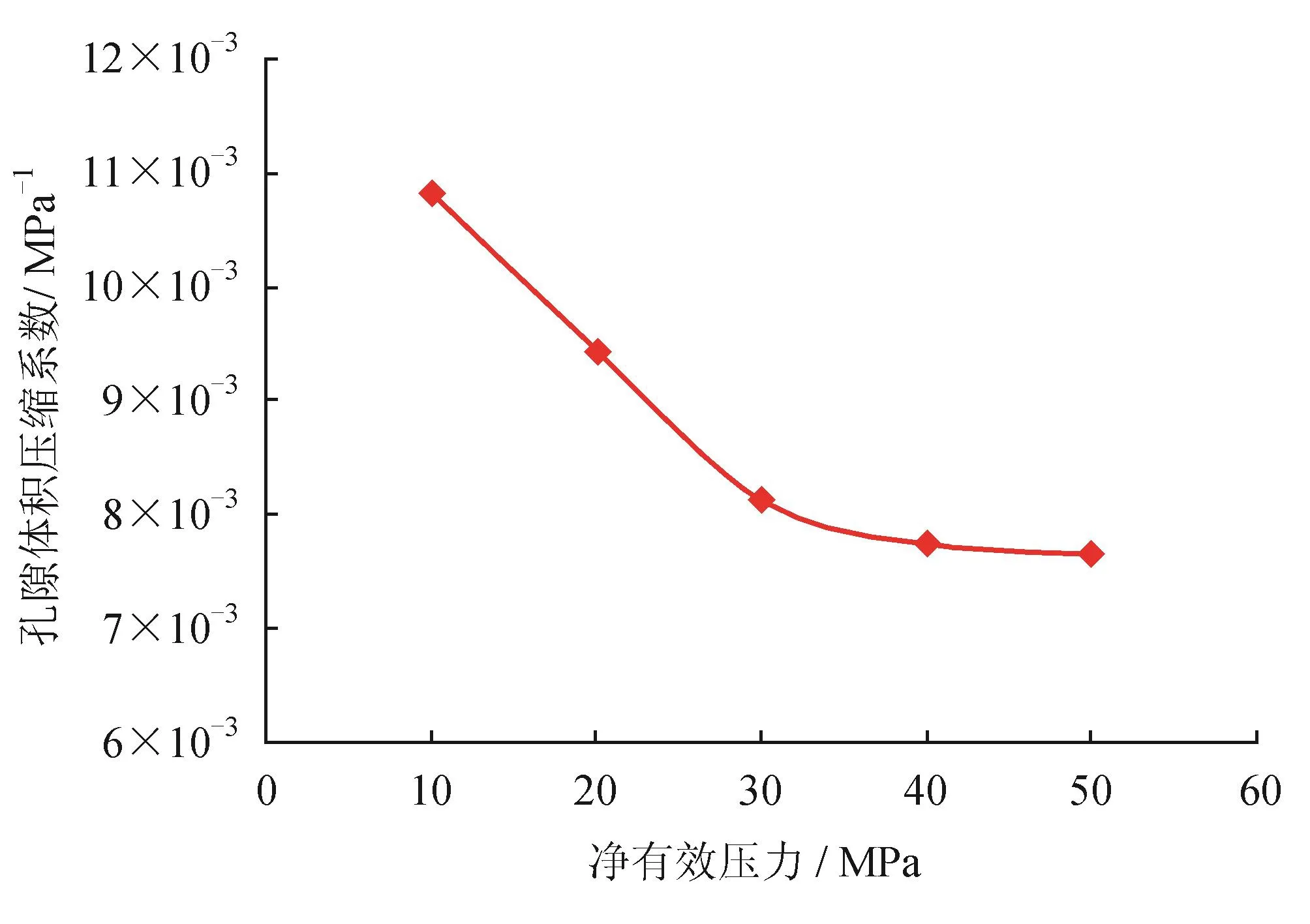
圖7 砂塞孔隙體積壓縮系數實驗結果圖

2.2 砂塞滲透率實驗

室內應用類似巖心夾持器工具制作人工模擬砂塞圓柱體，并在該工具中進行不同圍壓下砂塞滲透率測試，實驗后砂塞圓柱體如圖8所示。砂塞圓柱尺寸為r×h (10 mm×35 mm)，分別測試20目、40目、70目、100目陶粒。實驗設置5 MPa回壓，不同凈有效壓力下砂塞滲透率測試結果如圖9所示。

圖8 室內模擬砂塞圖

圖9 砂塞滲透率測試結果圖

滲透率實驗表明，砂塞滲透率隨凈有效壓力增加而下降，與孔隙體積壓縮系數類似。在整個凈有效壓力測試期間，砂塞滲透率在102～10－2D范圍內波動，當凈有效壓力超過20 MPa時砂塞滲透率隨凈有效壓力的變化趨于平緩。在相同凈有效壓力條件下，支撐劑目數越大，滲透率越高。

2.3 砂塞滲透率模型D—S參數求解

由縫內砂塞工程模擬實驗所得的孔隙體積壓縮系數及滲透率值可以解出基于接觸力學模型和分形理論的分形系數D、分維數S。擬合結果如圖10所示，分別解出不同目數支撐劑其分形系數D及分維數S。

3 縫內砂塞分段增產控制及優化

根據縫內砂塞強度理論、砂塞在流體作用下的穩定性及基于分形模型的滲透率函數關系，分析縫內砂塞在不同凈有效壓力、不同顆粒粒徑、不同楊氏模量條件下各個參數的變化規律，以進一步評價砂塞分段工藝的適應性。

3.1 支撐劑強度控制及優選

支撐劑顆粒滿足剪切破壞強度理論，如圖11所示：抗剪能力隨楊氏模量增加而增大；隨著外載荷增加，保持顆粒完整性所需的抗剪強度亦增加；在載荷增加初期，支撐劑顆粒需具有較高的抗剪強度。

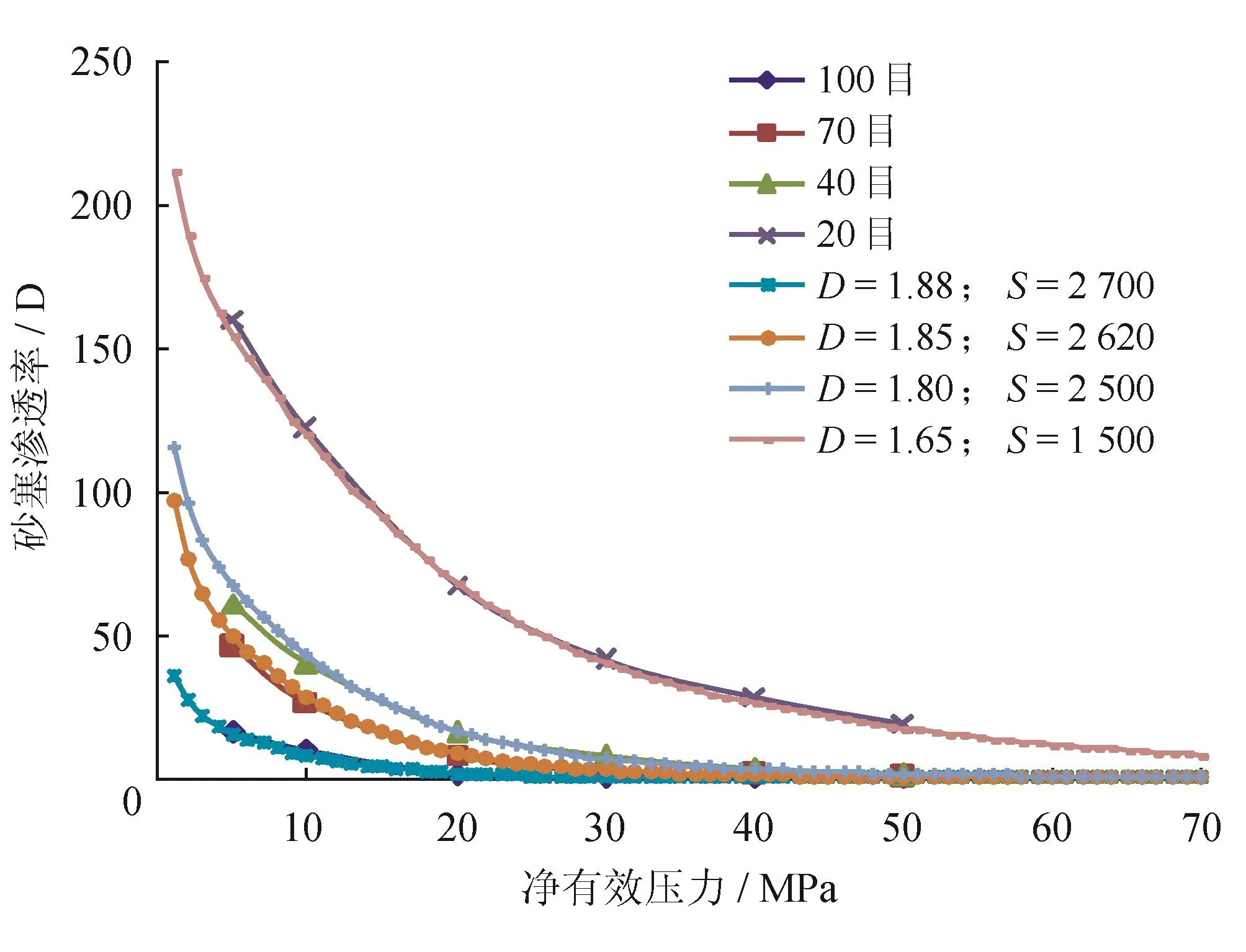
圖10 砂塞滲透率模型D—S擬合結果圖

圖11 支撐劑顆粒剪切破壞強度圖

顆粒之間的接觸區域半徑及形變均隨楊氏模量的增加、顆粒粒徑的減小、凈有效應力的減小而降低；接觸區域半徑及形變量均是在楊氏模量最小、顆粒粒徑最大、凈有效應力最大處取得最大值。在如圖12、13所示的參數范圍條件下，接觸區域半徑及形變量對凈有效應力、顆粒粒徑、楊氏模量的敏感程度依次減弱。

3.2 砂塞抗流體沖蝕控制及優化

支撐劑顆粒在縫內形成的砂塞受到沿流體運動方向的沖蝕作用力，而顆粒之間粗糙接觸表面的摩擦力是抵抗流體沖蝕力的主要貢獻者，二者之間的數量關系決定著縫內砂塞抗流體沖蝕作用的穩定性。

圖12 支撐劑顆粒接觸區域形變半徑圖

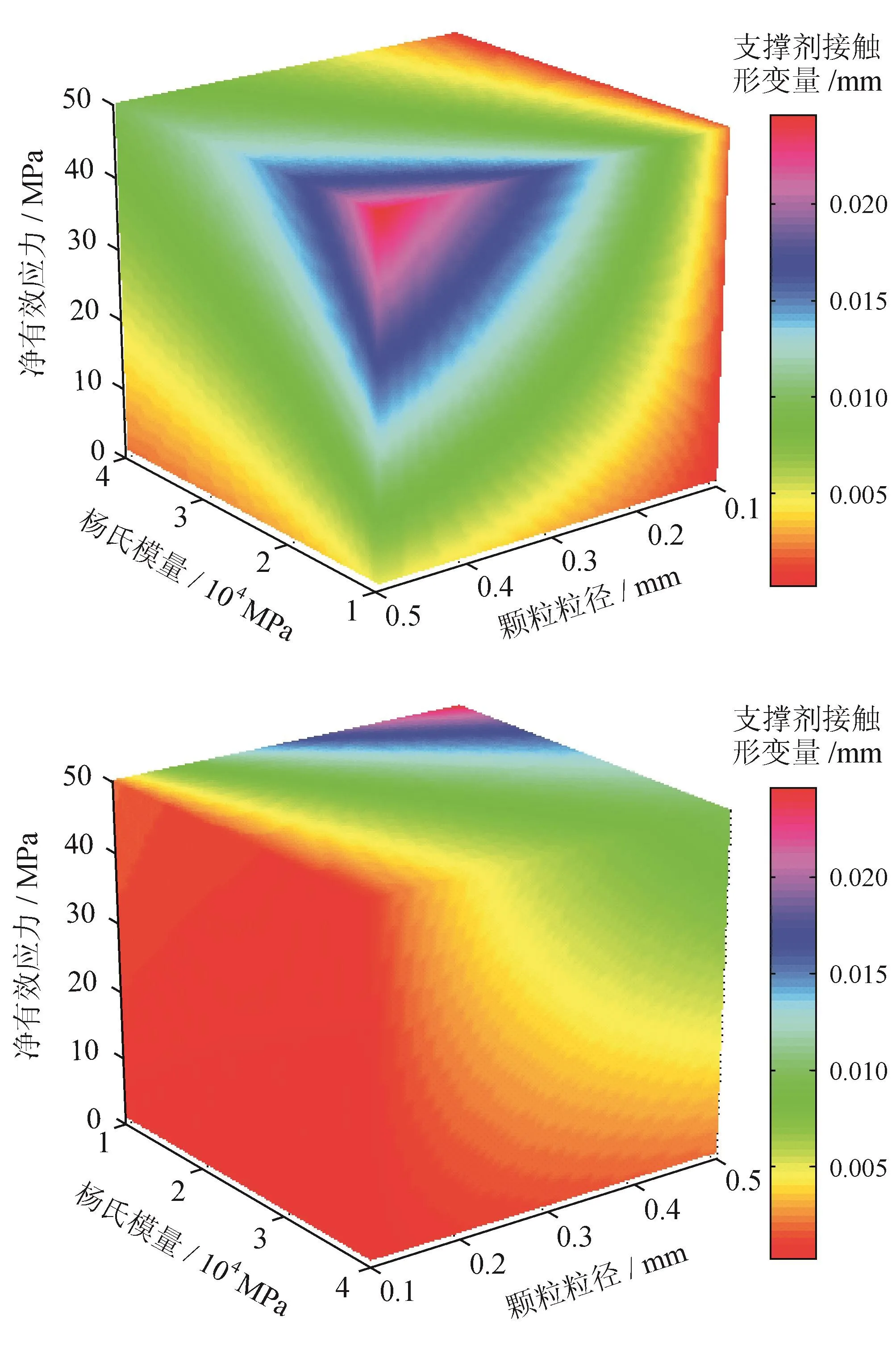
圖13 支撐劑顆粒接觸區域形變量圖

從圖14可以看出，支撐劑顆粒抗流體沖蝕能力隨顆粒粒徑的減小而降低，當支撐劑顆粒的粒徑小到一定值后，顆粒粒徑對支撐劑抗流體沖蝕能力的影響將逐漸減弱。接觸模型表征著顆粒之間的不同接觸關系，面心立方比體心立方接觸更為緊密，其受到的摩擦力更大。因此，面心立方相對體心立方穩定性更好。

以40目陶粒為例，計算在不同凈有效壓力條件下不同接觸模型抵抗流體沖蝕作用的流體參數。在圖15中，黃色、藍色面積分別表征面心、體心立方流體沖蝕參數（CDρR2V2）的取值范圍，面心立方的流體沖蝕參數近似體心立方的2倍。

3.3 砂塞滲透率分析

縫內砂塞滲透率大小對近井導流能力有著極為重要的影響。不同的接觸模型、不同支撐劑強度及粒徑等都將影響砂塞滲透率大小。以40目陶粒為例，其計算結果如圖16～18所示。

面心立方因其接觸較體心立方更為緊密，其在孔隙度及孔喉結構上要比體心立方致密。因此，面心立方砂塞的滲透率要比體心立方略小。支撐劑顆粒的楊氏模量與砂塞孔隙體積壓縮系數密切相關，楊氏模量通過影響孔隙體積壓縮系數而影響孔隙度及孔喉結構。圖18表明，高楊氏模量的支撐劑砂塞即使在高凈有效壓力條件下仍具有較高的滲透率，而對于低楊氏模量支撐劑砂塞，即使凈有效壓力不足10 MPa，其滲透率也小于1 D。顆粒粒徑主要通過影響孔喉結構而影響砂塞滲透率，支撐劑目數不同，分形系數及分維數皆不同。顆粒粒徑越大，砂塞滲透率越高。

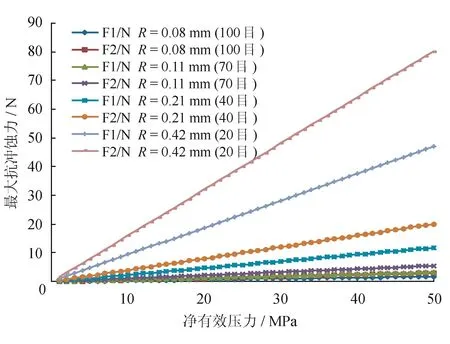
圖14 最大抗沖蝕力與顆粒粒徑關系圖

圖15 流體沖蝕參數與顆粒接觸模型關系圖

圖16 接觸模型與砂塞滲透率關系圖

圖17 砂塞孔隙度分布圖

圖18 砂塞滲透率分布圖

4 現場實踐與效果分析

ZC水平井位于四川盆地川南低陡褶帶南緣，南與滇黔北坳陷相鄰。該井以古生界下志留統龍馬溪組黑色頁巖為目的層，成像測井表明在水平段發育著不同傾角的高導縫。ZC井采用連續油管噴砂射孔＋縫內砂塞分段工藝進行增產改造，尾追階段采用240、300、400、480 kg/m3階梯砂濃進行縫內砂塞分段。砂塞均以40目陶粒為主，該陶粒的抗剪強度為50 MPa，楊氏模量為30 GPa，泊松比為0.25，視密度為2 600 kg/m3，靜摩擦系數為0.3，在12 m3/min排量下支撐劑砂塞的流體阻力系數為3。ZC井返排初期井口套壓為30 MPa，返排結束轉入投產時井口套壓為8 MPa。

圖19 砂塞抗剪強度圖

根據砂塞分段理論，ZC井砂塞接觸形變、滲透率及穩定性計算結果如圖19～21所示。由于ZC井水平段發育不同傾角的高導縫，因此在分析砂塞參數時必須考慮裂縫傾角的影響。支撐劑所需最大抗剪強度在傾角接近40°時取得最大值，砂塞滲透率在裂縫垂直、高楊氏模量處最大，而在傾角為40°時滲透率最小，其值在1 D左右。在本例中，當井口套壓為0時，裂縫傾角為40°左右處的支撐劑受到的剪切強度接近于其屈服強度，易發生支撐劑破碎損壞。

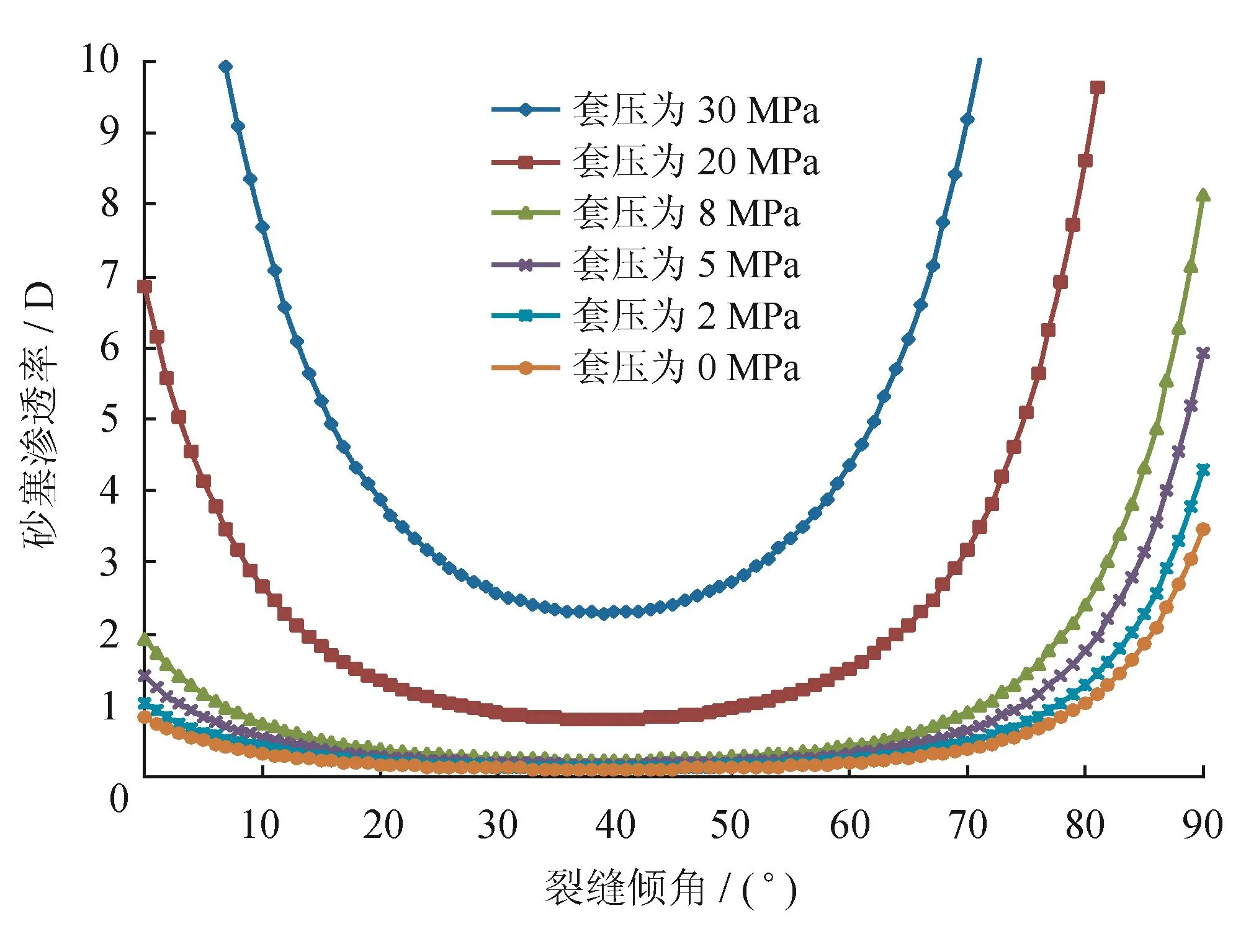
圖20 ZC井井口壓力與砂塞滲透率關系圖

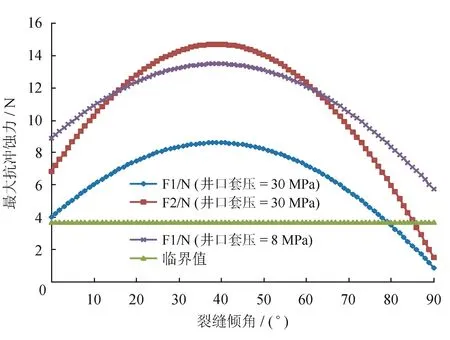
圖21 砂塞抗沖蝕能力圖

針對砂塞的抗沖蝕能力，選取返排初期進行模擬計算。在返排初期顆粒受到的流體壓力接近55 MPa，此時凈有效壓力較低，抵抗沖蝕作用的摩擦阻力較小。如圖21所示，體心立方（F1）模型的抗沖蝕能力比面心立方（F2）的抗沖蝕能力弱，當裂縫傾角分別高于78°、85°時，體心立方、面心立方模型中分別將發生部分支撐劑被流體沖塌現象。

ZC井應用縫內砂塞分段壓裂工藝，現場分段效果如圖22、23所示，各段起裂信號均出現在壓裂設計層段位置，無起裂信號串層現象。微地震監測結果表明各層段均實現了有效封隔，改造規模達到了設計的改造體積，壓后返排取得測試產量12×104m3/d（13 mm油嘴，井口套壓8 MPa）。

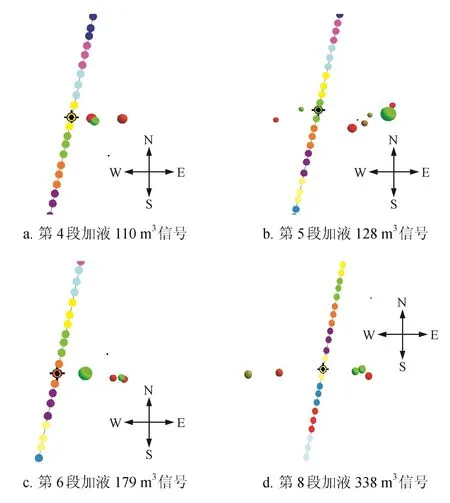
圖22 ZC井第4、5、6、8段起裂信號圖

圖23 ZC井微地震監測分段效果圖

5 結論與建議

通過前文建立的支撐劑顆粒接觸模型及在閉合應力與流體沖蝕作用下的穩定性、砂塞滲透率等基礎研究，對ZC井的砂塞封堵參數進行了優化，經過20段現場壓裂實踐，進一步驗證了該系列模型的適應性，得到如下認識。

1）應用球體密集堆積理論結合Hertz彈性球體點載荷接觸力學所建立的支撐劑顆粒接觸模型，能夠良好地表征縫內砂塞的接觸、受力等關系，應用分形理論表征砂塞滲透率值與實驗實測模擬砂塞滲透率值，能夠建立良好的數學關系，該砂塞滲透率模型對現場應用具有一定的指導意義。

2）在返排初期砂塞的穩定性主要受到流體的沖蝕作用影響，應嚴格控制排液速率，在生產后期砂塞的穩定性主要受到裂縫閉合應力和流壓的影響，適當提高支撐劑顆粒的屈服強度對穩產具有重要意義。

3）支撐劑顆粒的楊氏模量通過影響孔隙度和孔喉結構而影響滲透率，支撐劑粒徑主要通過影響孔喉結構而影響滲透率，提高支撐劑的楊氏模量是保持裂縫較高滲透率及導流能力的最有效方法。

4）針對支撐劑顆粒抗流體的沖蝕能力，支撐劑顆粒靜摩擦系數、流體阻力系數及實際流速等參數需進一步開展相關實驗，以完善相應研究。

[1] Jaripatke OA, Chong KK, Grieser WV & Passman A. A completions roadmap to shale-play development: A review of successful approaches toward shale-play stimulation in the last two decades[C]//International Oil and Gas Conference and Exhibition in China, 8-10 June 2010, Beijing, China. DOI: http://dx.doi.org/10.2118/130369-MS.

[2] Cipolla CL, Warpinski NR, Mayerhofer MJ, Lolon E & Vincent MC. The relationship between fracture complexity, reservoir properties, and fracture treatment design[C]//SPE Annual Technical Conference and Exhibition, 21-24 September 2008, Denver,Colorado, USA. DOI: http://dx.doi.org/10.2118/115769-MS.

[3] 梁興, 朱炬輝, 石孝志, 張俊成, 劉臣, 何封, 等. 縫內填砂暫堵分段體積壓裂技術在頁巖氣水平井中的應用[J]. 天然氣工業, 2017, 37(1): 82-89.Liang Xing, Zhu Juhui, Shi Xiaozhi, Zhang Juncheng, Liu Chen,He Feng, et al. Staged fracturing of horizontal shale gas wells with temporary plugging by sand ベlling[J]. Natural Gas Industry,2017, 37(1): 82-89.

[4] Dai Hongqin, Bai Lun, Zhan Kuihua, Sun Ziling & Guan Guoping. Computer simulation of random packing of spherical particles in two dimensions[J]. Journal of Donghua University (English Edition), 2011, 28(1): 31-34.

[5] 葉大年. 球體任意堆積的統計幾何分析[J]. 地質科學,1990(4): 324-331.Ye Danian. Statistical geometrical analysis of haphazard packing of spheres[J]. Scientia Geologica Sinica, 1990(4): 324-331.

[6] 徐芝綸. 彈性力學[M]. 4版. 北京: 高等教育出版社, 2006.Xu Zhiguan. Elastic mechanics[M]. 4thed. Beijing: High Education Press, 2006.

[7] Johnson KL. 接觸力學[M]. 徐秉業, 譯. 北京: 高等教育出版社, 1992.Johnson KL. Contact mechanics[M]. Xu Bingye, trans. Beijing:High Education Press, 1992.

[8] 云天銓. Hertz接觸問題的精確的積分方程[J]. 應用數學和力學, 1991, 12(2): 165-169.Yun Tianquan. The exact integral equation of Hertz's contact problem[J]. Applied Mathematics and Mechanics, 1991, 12(2):165-169.

[9] Pimenov AA & Kanevskaya RD. Mathematical modeling of proppant embedment and its effect on conductivity of hydraulic fracture[C]//SPE Russian Petroleum Technology Conference,16-18 October 2017, Moscow, Russia. DOI: http://dx.doi.org/10.2118/187934-MS.

[10] Zhang Junjing, Ouyang Lianchen, Hill AD & Zhu Ding. Experimental and numerical studies of reduced fracture conductivity due to proppant embedment in shale reservoirs[C]//SPE Annual Technical Conference and Exhibition, 27-29 October 2014, Amsterdam, The Netherlands. DOI: http://dx.doi.org/10.2118/170775-MS.

[11] 吳國濤, 胥云, 楊振周, 楊立峰, 張靜. 考慮支撐劑及其嵌入程度對支撐裂縫導流能力影響的數值模擬[J]. 天然氣工業,2013, 33(5): 65-68.Wu Guotao, Xu Yun, Yang Zhenzhou, Yang Lifeng & Zhang Jing.Numerical simulation considering the impact of proppant and its embedment degree on fracture ぼow conductivity[J]. Natural Gas Industry, 2013, 33(5): 65-68.

[12]侯磊, Elsworth D, 孫寶江, 王金堂. 頁巖支撐裂縫中滲透率變化規律實驗研究[J]. 西南石油大學學報(自然科學版), 2015,37(3): 31-37.Hou Lei, Elsworth D, Sun Baojiang & Wang Jintang. Experimental study on permeability evolution in propped shale fracture[J].Journal of Southwest Petroleum University (Science & Technology Edition), 2015, 37(3): 31-37.

[13] 陳國輝. 球體在接觸中發生破壞的預見和計算[J]. 貴州工學院學報, 1984(增刊1): 141-148.Chen Guohui. The prediction and calculation of the failure of a sphere in contact[J]. Journal of Guizhou University of Technology, 1984(S1): 141-148.

[14] 瓦倫丁 L 波波夫. 接觸力學與摩擦學的原理及其應用[M]. 李強, 雒建斌, 譯. 北京: 清華大學出版社, 2011.Popov VL. Contact mechanics and friction physical principles and applications[M]. Li Qiang & Luo Jianbin, trans. Beijing: Tsinghua University Press, 2011.

[15] 楊勝來, 魏俊之. 油層物理學[M]. 北京: 石油工業出版社,2004.Yang Shenglai & Wei Junzhi. Petrophysics[M]. Beijing: Petroleum Industry Press, 2004.

[16] 李留仁, 趙艷艷, 李忠興, 焦李成, 薛中天. 多孔介質微觀孔隙結構分形特征及分形系數的意義[J]. 石油大學學報(自然科學版), 2004, 28(3): 105-107.Li Liuren, Zhao Yanyan, Li Zhongxing, Jiao Licheng & Xue Zhongtian. Fractal characteristics of micropore structure of po-rous media and the meaning of fractal coefベcient[J]. Journal of the University of Petroleum, China (Edition of Natural Science),2004, 28(3): 105-107.

[17] 李留仁, 袁士義, 胡永樂. 分形多孔介質滲透率與孔隙度理論關系模型[J]. 西安石油大學學報(自然科學版), 2010, 25(3):49-51.Li Liuren, Yuan Shiyi & Hu Yongle. A new model for describing the relationship between the permeability and the porosity of fractal porous media[J]. Journal of Xi'an Shiyou University (Natural Science Edition), 2010, 25(3): 49-51.

[18] 杜殿發, 趙艷武, 張婧, 劉長利, 唐建信. 頁巖氣滲流機理研究進展及發展趨勢[J]. 西南石油大學學報(自然科學版),2017, 39(4): 136-144.Du Dianfa, Zhao Yanwu, Zhang Jing, Liu Changli & Tang Jianxin. Progress and trends in shale gas seepage mechanism research[J]. Journal of Southwest Petroleum University (Science &Technology Edition), 2017, 39(4): 136-144.

[19] 鄢雪梅, 王欣, 張合文, 王永輝, 段瑤瑤. 頁巖氣藏壓裂數值模擬敏感參數分析[J]. 西南石油大學學報(自然科學版),2015, 37(6): 127-132.Yan Xuemei, Wang Xin, Zhang Hewen, Wang Yonghui & Duan-Yaoyao. Analysis of sensitive parameter in numerical simulation of shale gas reservoir with hydraulic fractures[J]. Journal of Southwest Petroleum University (Science & Technology Edition),2015, 37(6): 127-132.

[20] 賈成業, 賈愛林, 何東博, 位云生, 齊亞東, 王軍磊. 頁巖氣水平井產量影響因素分析[J]. 天然氣工業, 2017, 37(4): 80-88.Jia Chengye, Jia Ailin, He Dongbo, Wei Yunsheng, Qi Yadong &Wang Junlei. Key factors influencing shale gas horizontal well production[J]. Natural Gas Industry, 2017, 37(4): 80-88.