裝配式梁橋整體托換裝置及瞬態沖擊效應研究

黃海新，李曉迪，程壽山，韓立中

（1.河北工業大學 土木與交通學院，天津 300401；2.交通運輸部公路科學研究所，北京 100080）

0 引言

近年來我國橋梁建設成績斐然，其中裝配式混凝土梁橋在中小跨徑結構中占比很大.但由于承載能力提升、年久失修結構劣化嚴重等原因，部分結構需拆除更換[1].傳統的拆除方法是采用大型吊車、浮吊等進行單片切割吊拆后單片安裝[2]，但該方法對橋梁下部凈空要求較高，尤其對橋下有通航、通行要求的結構更是存在干擾大、風險高，難以實施的問題.

針對上述問題，本文以一跨線裝配式混凝土梁橋為工程背景，提出了一種施工簡便快捷、安全性高，對交通運營幾乎無干擾的整體托換裝置，同時就該裝置平移瞬間的沖擊效應進行了研究，所得結論對工程實踐具有一定的指導意義.

1 工程概況及改造方案

某裝配式混凝土梁橋，橋梁上部結構為1×13 m鋼筋混凝土T梁，橫向布置6片，梁高1.3 m，設6道橫隔板（見圖1）.該橋經檢測評定為五類橋，需拆除重建.

由于該橋跨客運專線，梁底距高壓線很近，傳統單片拆除單片安裝的方式難以適用.為此，在吸收借鑒橋梁中頂推法[3]和建筑中整體平移技術[4]的基礎上，提出了一種整體托換改造裝置，如圖2所示.

托換改造裝置設在待拆梁體上部，由鋼構件拼裝而成.主要包括設置在橋臺兩側支撐在現澆混凝土橫梁上的鋼立柱、柱頂部工字鋼端橫梁、縱梁和移動橫梁.其中，縱梁上設置副滑道，移動橫梁在其上滑動，橫梁通過柔性吊桿與設于待拆梁體一端的底部兜底橫梁相連，混凝土梁體的另一段采用剛性滑動支承，并將在設于橋跨外側的主滑道上滑動.既有裝配式混凝土梁體拆除過程為先進行豎向頂升，既而利用卷揚機拖曳梁體將其整體移出既有線路后破拆.新梁更換安裝時工藝流程與拆除相反，即采用先在橋跨外側整體組拼，而后整體平移到橋位處落梁.

主副滑道和剛柔兩種支撐方式的設置，不同于一般的整體平移裝置，這也導致了在整個平移過程中，下部主梁整體在卷揚機的牽引下先勻速移動，至吊桿傾斜至一定角度后移動橫梁才能開始移動，而由于靜動摩擦的瞬態切換勢必導致移動橫梁對結構產生沖擊效應，這對結構帶來的影響究竟有多大，其變化規律如何值得進一步探討.

圖1 橋梁工程圖Fig.1 Photo of bridge

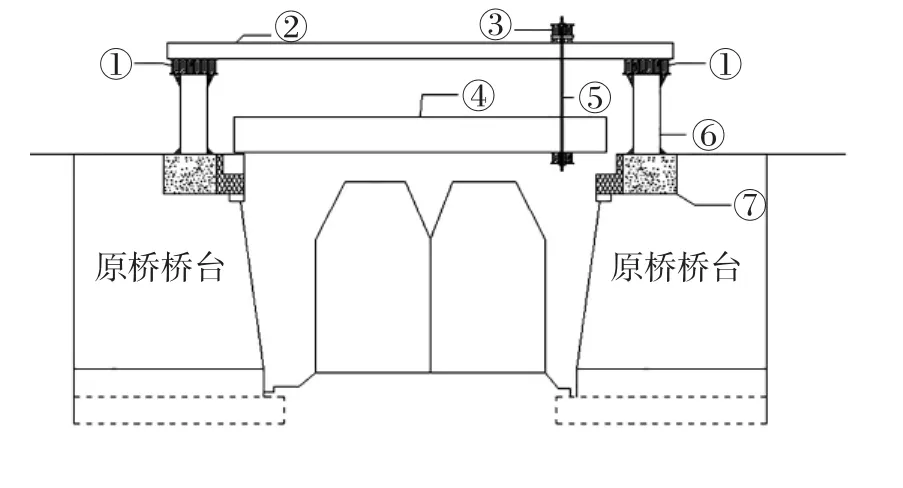
圖2 橋梁改造立面圖Fig.2 Elevation of bridge rehabilitation

2 理論分析

2.1 動力學方程的建立

以裝置中移動橫梁為研究對象，其簡化的力學計算模型如圖3所示.

設上部移動橫梁開始運動作為t=0時刻，根據達朗伯原理，可得移動橫梁受力應滿足如下平衡方程式

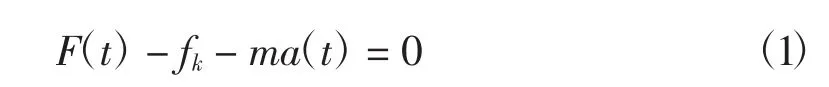
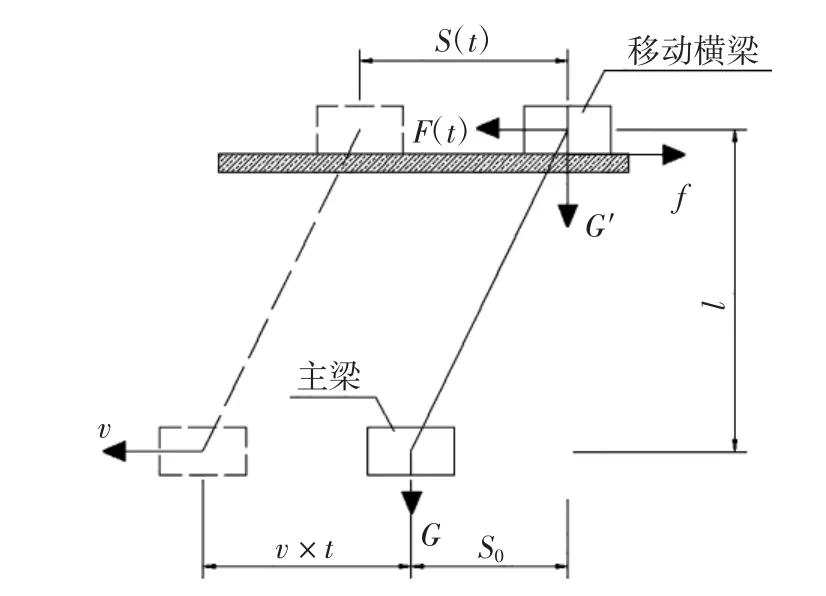
圖3 移動橫梁力學計算模型Fig.3 Mechanical model of moving crossbeam

橫梁即將移動時刻力矩平衡，可得方程

在移動橫梁即將移動時，應有

式中：F（t）為移動橫梁所受的水平分力，N；fk為移動橫梁所受的滑動摩擦力，N；m為移動橫梁的質量，kg；a（t）為移動橫梁移動過程中的加速度，m/s2；G′為移動橫梁所受的豎向分力，N，由圖2中結構布局知，其為下部混凝土主梁自重的一半；S0為移動橫梁即將移動時與下部混凝土主梁的位移差值，m；S（t）為移動橫梁的位移，m；v為混凝土主梁平移速度，m/s；t為移動橫梁運動的時間，s；fs為移動橫梁所受的最大靜摩擦力，N；l為移動橫梁與混凝土主梁豎向垂直距離，m.

需要說明的是，這里摩擦力按照正壓力與摩擦系數的乘積計算，且假定摩擦系數為常量，即

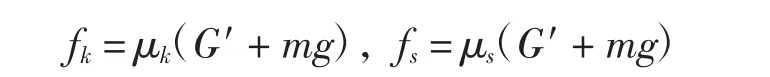
其中，μk和μs分別為動、靜摩擦系數.

聯立式 （1） 和式（2），可得

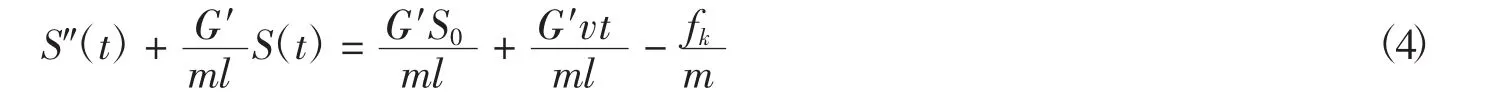
將式（3） 代入式（4），得微分方程通解為

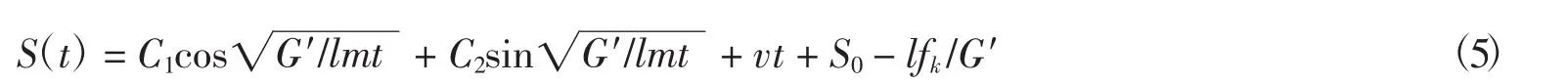
在t=0時，有初始條件S（0）=0，S′（0）=0，代入式（5）可得

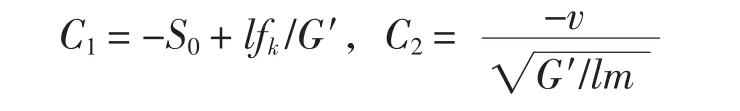
將改造工程中相關數據代入上式，可得移動橫梁位移表達式

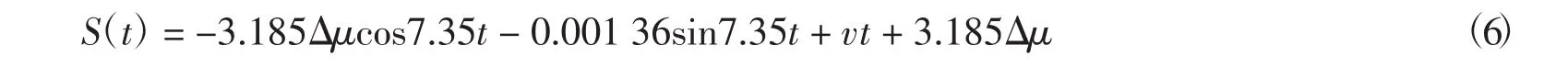
由式（6）可知，移動橫梁位移與移動橫梁靜動摩擦系數的差值、下部混凝土梁體移動速度v有關.

2.2 梁體運動協調性分析

基于上述方程（6）可以獲得移動橫梁自身的位移時程曲線，但對工程而言，技術人員可能更關心移動初期，由于靜動摩擦的瞬態切換對改造裝置及混凝土梁體本身帶來的沖擊效應，以及上部移動橫梁移動后和下部混凝土梁體間的相對位置關系，因為這直接涉及到上下部梁體運動的協調性，而這會對結構產生不同程度的影響.

為此，這里著重分析靜動摩擦系數的不同比值對上下部梁體運動協調性的影響，希望找到移動橫梁追上下部混凝土主梁的臨界點.

假定下部混凝土主梁以速度v勻速運動，由于移動橫梁初始時刻存在位移差S0，因此當vt+S0≤S（t）時，移動橫梁才能追上混凝土主梁.結合式（5），得移動橫梁與下部混凝土主梁位移差值表達式為

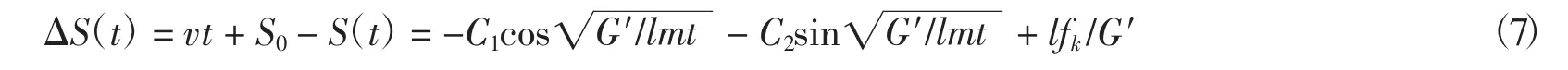
移動橫梁若能追上下部混凝土梁體，應有△S（t）≤0.由式（8）解得

可見，當動靜摩擦系數的比值等于0.5時，后期移動的移動橫梁即可追上下部先移動的混凝土主梁，由此可獲得二者運動位置的臨界狀態△Smin=0.

將改造工程中相關數據代入，上下部梁體位移差值可表示為

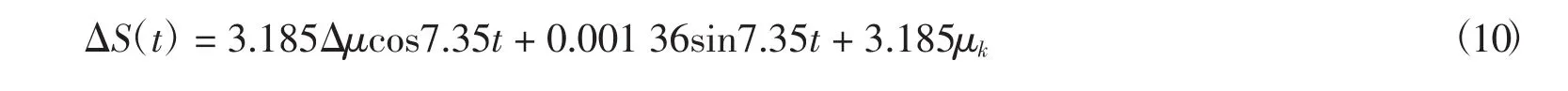
3 數值模擬

數值模擬的目的，一方面檢驗前面建立的移動橫梁運動方程的正確性，同時可更為直觀地全程展示移動橫梁及其與下部梁體間位置關系及受靜動摩擦系數的影響，尤其便于體現理論表達式未計入的瞬態沖擊效應的強烈程度.

3.1 模型建立

利用Abaqus軟件對梁體平移過程進行模擬.限于電腦內存并為縮短運營時間，根據分析重點，將模型加以簡化，即將混凝土梁體簡化為一長方體質量塊，上部縱梁固定，忽略鋼立柱及端橫梁，縱梁和頂部移動橫梁間設置為滑動接觸，動、靜摩擦系數均假定為常量.移動橫梁通過兩根吊桿與下部梁體相連，模型如圖4所示.

3.2 仿真分析

3.2.1 模型檢驗

圖5給出了在靜摩擦系數μs=0.06的情況下的移動橫梁上吊點處節點理論計算和數值模擬結果位移對比情況.

從圖5可見，理論和數值計算結果吻合較好，驗證理論模型正確性的同時，亦表明有限元數值模型的精度，混凝土梁體的平移過程可通過該模型仿真模擬.

3.2.2 工況選取及模擬結果

根據前面的理論推導，在設定下部混凝土主梁平移速度為0.01 m/s的前提下，按照移動橫梁能否追上下部梁體的情況，選取3種不同的動、靜摩擦系數組合工況進行分析.其中，動摩擦系數μk根據相關資料[8]選取0.03，靜摩擦系數μk則分別取：工況①0.05；工況②0.06；工況③0.11.

圖6～圖8分別給出了3種靜動摩擦系數工況下移動橫梁和下部梁體的位移時程變化.此外，為量化體現沖擊效應的強烈程度，這里同時給出了混凝土主梁吊點處應力變化曲線.

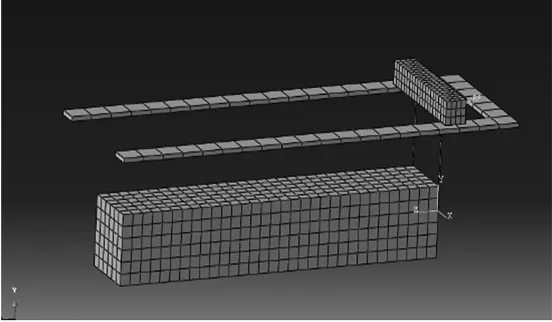
圖4 簡化有限元模型Fig.4 Simplified finite element model

圖5 移動橫梁吊點處節點理論和數值結果位移對比圖（μs=0.06）Fig.5 Theoretical and numerical displacement of moving crossbeam（μs=0.06）

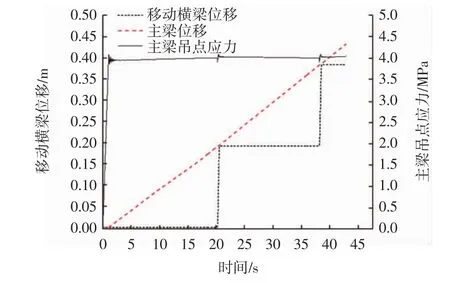
圖7 移動橫梁位移、主梁位移及其吊點處主應力（μs=0.06）Fig.7 Displacement of moving crossbeam and mainbeam as well as stress of mainbeam suspension element（μs=0.06）

3.2.3 結果分析

就主梁平移過程中上下部梁體的位移時程而言，從圖6～圖8可以看出，主梁位移一直均勻增加，而移動橫梁則出現從移動到靜止，再從靜止到移動的周期性變化，具體為先為下部主梁整體勻速移動，結合圖3知移動橫梁至吊桿傾斜至一定角度后才開始移動，且移動迅速，有時甚至超過下部主梁右端，之后靜止，等到第2次拉起再移動，往復進行.其原因在于，初期主梁移動吊桿傾角較小，此時拉力小于最大靜摩擦力，移動橫梁不會同步移動，在吊桿傾斜至一定角度后，吊桿拉力隨之增大到最大靜摩擦力，移動橫梁開始移動.移動瞬間由于動、靜摩擦系數的切換，摩擦力減小至滑動摩擦力，而吊桿拉力此時由于滯后性仍為最大靜摩擦力，移動橫梁迅速向前加速移動，吊桿傾斜角度逐漸變小，直到吊桿拉力減小到動摩擦力，此時移動橫梁由于慣性繼續向前減速移動，Δμ較大時甚至超過下部梁體右端，之后隨著動能下降而靜止.而后，照此周期性運動.圖6中工況①表明，μs取0.05時，移動橫梁整個平移過程中一直滯后于下部混凝土主梁；圖7中μs取0.06時，上下部梁體某個時刻可正好處于相遇的臨界狀態；圖8中μs取0.11時，則出現了上部移動橫梁可追上并超越主梁的現象，這些現象與理論推導的結論均一致.

在不同μs情況下，對比移動橫梁位移圖可知，μk保持不變，μs越大，移動橫梁初始移動時間越晚，其原因可由前面理論推導解釋，根據理論分析，兩梁體初始位移差為S0=3.185μs，隨著μs的增大，S0逐漸增大，即吊桿傾角越大，3種工況下主梁移動速度不變，故有移動橫梁初始移動時間必然隨著μs的增大而推遲.

為清晰體現移動橫梁的靜動摩擦瞬態切換對結構帶來的沖擊效應，這里將移動橫梁移動瞬間對應的主梁吊點處主應力（遵循von Mises應力準則）時程曲線加以局部放大，如圖9～圖11所示.

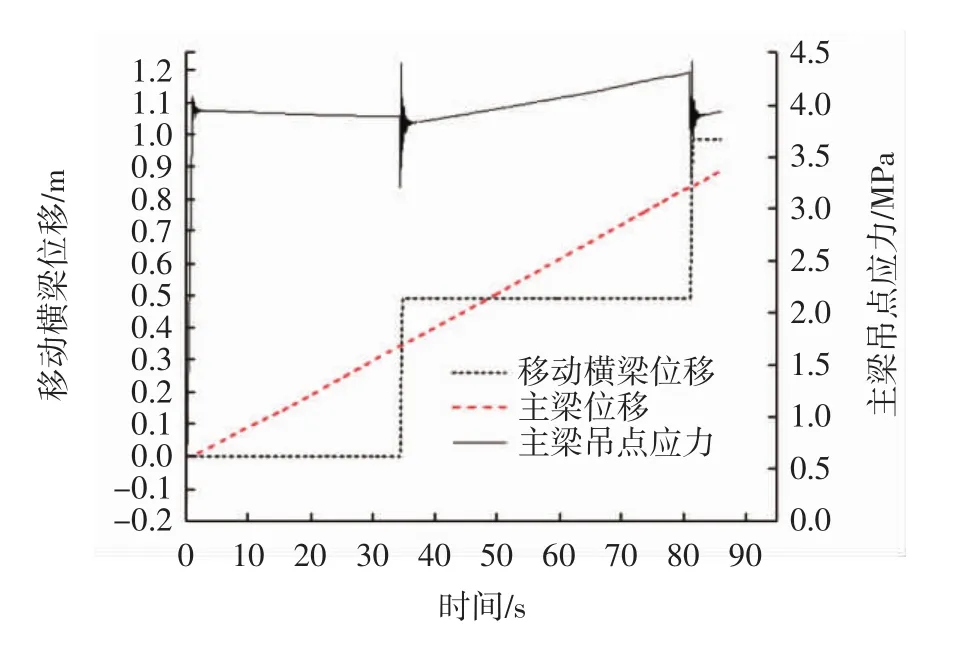
圖8 移動橫梁位移、主梁位移及其吊點處單位主應力（μs=0.11）Fig.8 Displacement of moving crossbeam and mainbeam as well as stress of mainbeam suspension element（μs=0.11）

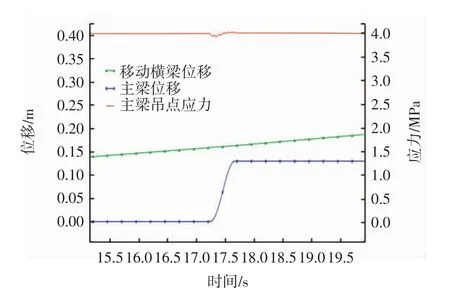
圖9 移動橫梁位移、主梁位移及其吊點處主應力局部放大圖（μs=0.05）Fig.9 Local displacement of moving crossbeam and mainbeam as well as stress of mainbeam suspension element（μs=0.05）

從圖中可見，3種工況下移動橫梁移動的瞬間主梁吊點處的應力均呈現先突然減小而后增加的變化.分析該現象，應該是由于移動橫梁在動靜摩擦力切換瞬間突然移動，導致下部梁體產生向下的加速度，吊桿拉力突減所致，這一點可從影響主梁吊點應力的主要分量σy的突然下降可知（見圖12）.而當移動橫梁靜止后，吊桿拉力逐漸恢復，下部梁體吊點處應力增大.

對比3種工況模擬結果，可知雖然主梁吊點處應力變化總趨勢相同，但在移動橫梁開始運動到靜止的一個周期內，主梁最大值出現的時刻及應力波動變化的程度不同.工況①中移動橫梁未追上主梁，應力最大值出現在移動橫梁即將靜止前兩梁體水平位移差最小的時刻；工況②中移動橫梁恰好在靜止時追上主梁，應力最大值出現在移動橫梁靜止的時刻；工況③中移動橫梁追上并超越主梁，應力最大值出現在移動橫梁剛好追上主梁的時刻.總體來說，3組主梁應力最大值均出現在兩梁體水平位移差最小的時刻.

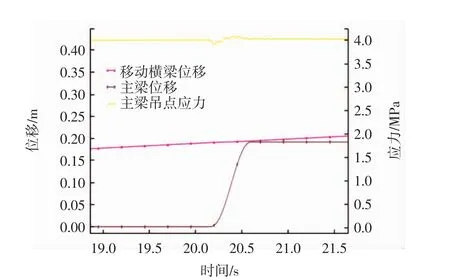
圖10 移動橫梁位移、主梁位移及其吊點處主應力局部放大圖（μs=0.06）Fig.10 Local displacement of moving crossbeam and mainbeam as well as stress of mainbeam suspension element（μs=0.06）

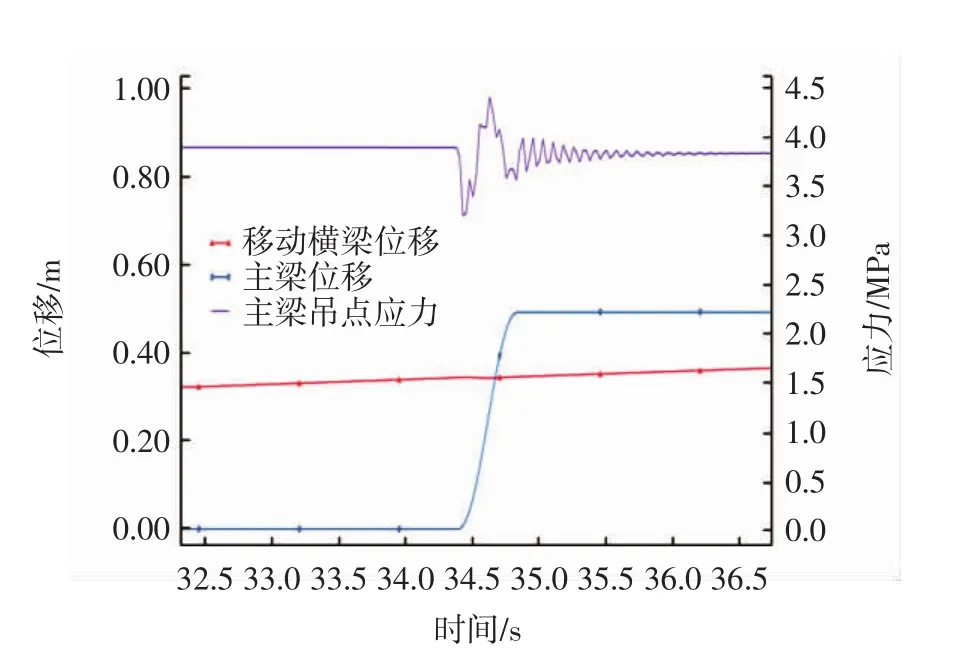
圖11 移動橫梁位移、主梁位移及其吊點處主應力局部放大圖（μs=0.11）Fig.11 Local displacement of moving crossbeam and mainbeam as well as stress of mainbeam suspension element（μs=0.11）

表1中給出了3種工況下混凝土主梁吊點處應力數值.可見，工況①中主梁一個周期內應力最大變化幅度為2.5%；工況②中主梁一個周期內應力最大變化幅度為4.7%；工況③中主梁一個周期內應力最大變化幅度為37.3%.前2個工況應力波動變化幅度較小，對結構沖擊效應不明顯，而工況③應力變化幅度顯著，對結構帶來了一定程度的沖擊效應，不過好在仍小于混凝土梁體的容許應力，可以確保主梁平穩出入橋位.

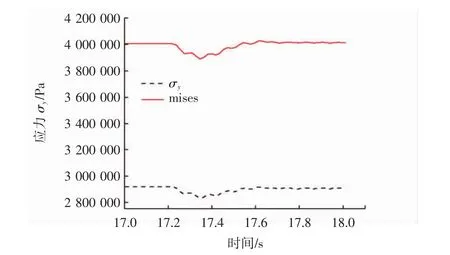
圖12 主梁吊點單元應力與豎向分應力σy圖Fig.12 Stress of mainbeam suspension element as well as vertical stress（μs=0.05）

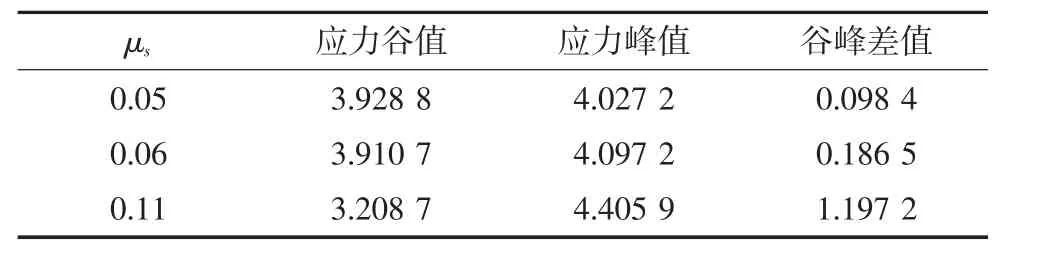
表1 主梁吊點處單元應力MPaTab.1 Stress of mainbeam element at suspension node

4 結論

1） 針對橋下改造空間受限的裝配式混凝土梁橋，傳統的單片切割拆除單片安裝的改造技術難以適用的狀況，給出了一種剛柔支撐的整體托換裝置，該裝置由常規鋼構件組拼而成，上下部設置主副滑道，在卷揚機的牽引下移動，具有施工簡便，無需大型起吊機具、造價低、工期短、對周邊環境影響小的特點.

2）基于達朗伯原理，建立了移動橫梁動力學方程，該方程能考慮靜動摩擦系數的影響，并能體現主梁平移過程中與上部移動橫梁間的位置關系，理論推得動靜摩擦系數比值0.5是移動橫梁能否追上下部梁體的臨界點.

3）選取混凝土梁體吊點處的應力，研究靜動摩擦切換瞬間的沖擊效應.結果表明，移動橫梁移動瞬間主梁吊點處應力突然減小，而后梁體吊點處應力最大值出現在移動橫梁與主梁水平位移最小的時刻.

[1] 桂學.橋梁頂升技術研究[D].西安：長安大學，2005.

[2] 楊顯維，楊文強.混凝土梁式橋拆除技術分析[J].天津建設科技，2013，23（5）：57-59.

[3] 宋延旭．頂推施工階段鋼箱梁橋受力性能研究[D]．北京：北京交通大學，2010.

[4] 袁放.既有線上跨橋梁同步頂升與平移技術研究[D].上海：華東交通大學，2010.

[5] 程海根.鄒常進.同步頂升解決跨線橋凈空問題關鍵技術探討[C]//第十八屆全國橋梁學術會議，2008.

[6] 臧小萌.淺談七里河黃河大橋主橋上部結構拆除方法[J].甘肅科技，2011，23（24）：129-130.

[7] 石亦平，周玉蓉.ABAQUS有限元分析實例詳解[M].北京：機械工業出版社，2006.

[8] 張俊義.橋梁施工常用數據手冊[M].北京：人民交通出版社，2005.

[9] 陳松，卓靜，朱雪源.一種小跨徑橋梁快速改造新技術[J].公路工程，2016，41（1）：81-84.

[10]姚玲森．橋梁工程[M].北京：人民交通出版社，2012.

[11]蔣巖峰.移位技術在橋梁改造中的應用[J].中國公路，2011（13）：86-89.

[12]李小軍.64 m系桿拱梁橫移施工技術[J].中國公路，2011（7）：180-181.

[13]Beaney N J，Martin J M.Design and construction of Dornoch Firth Bridge[C]//Construction Proceedings of Institution Civil Engineering.Transportation，Aug 1993.

[14]黃僑，趙銀飛，孫永明.大跨度提籃式人行拱橋的振動病害分析與改造[J].公路交通科技，2008，25（10）：88-92.

[15]衛星，強士中，高偉.舊橋加固中的一種常用方法[J].公路交通科技，2002，19（5）：85-87.

[16]封建武.高速公路上跨橋整體頂升技術[J].城市道橋與防洪，2008，2（2）：52-55.

[17]劉富勤.整體平移技術在城區改造中的應用研究[D].武漢：武漢理工大學，2005.

[18]李愛群，吳二軍.我國建筑物整體平移技術及工程應用進展[J].江蘇建筑，2003（S）：48-54.