中國郵遞員問題奇偶點圖上作業法最優標準的商榷

王邦兆 陳永清 王海軍 魏志祥

摘要：論文討論了關于中國郵遞員問題的一種誤解，分析了產生誤解的原因，提出了解決中國郵遞員問題的指派問題模型。

Abstract： This paper discusses a misunderstanding about the Chinese Postman Problem， analyzes the causes of misunderstanding， and proposes a assignment problem model to solve the Chinese Postman Problem.

關鍵詞：中國郵遞員問題;奇偶點圖上作業法;指派問題

Key words： Chinese Postman Problem; odd-even-point graphical operation method; assignment problem

中圖分類號：O157.5? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標識碼：A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文章編號：1006-4311（2018）36-0258-02

1? 中國郵遞員問題與圖上作業法

郵遞員每天從郵局出發，走遍該地區所有街道再返回郵局，問題是他應如何安排送信的路線可以使所走的總路程最短。這個問題由中國學者管梅谷在1960年首先提出的，他給出了解法——“奇偶點圖上作業法”，被國際上統稱為“中國郵遞員問題”。用圖論的語言描述，給定一個連通圖G，每邊e有非負權），要求一條回路經過每條邊至少一次，且滿足總權最小[2]。中國郵遞員問題的研究受到了國內外學者的廣泛關注，國外最早研究中國郵遞員問題的是J.Edmonds，他把中國郵遞員問題稱為Chinese Postman Problem（簡稱CPP）。國內研究中國郵遞員問題的學者更多，產生了一批優秀的成果。馮俊文[3]提出了中國郵遞員問題的整數規劃模型，李念祖[4]提出了中國郵遞員問題的完全最優子圖算法，汪海森[5]等提出了中國郵遞員問題的匹配算法，金毅[6]對中國郵遞員問題進行了數理分析。

奇偶點圖上作業法的基本思想：如果郵遞員負責投遞范圍的街道圖中沒有奇點，它就是歐拉圖，郵遞員只要經過所有街道一次且僅一次，就能得到最短的路徑;如果街道圖中有奇點，將奇點兩兩配對，重復配對的兩個奇點間的一條鏈，就可以得到歐拉圖，如果重復的路徑的總長度達到最短，就得到了最優解。

2? 對奇偶點圖上作業法最優標準的誤解及其原因分析

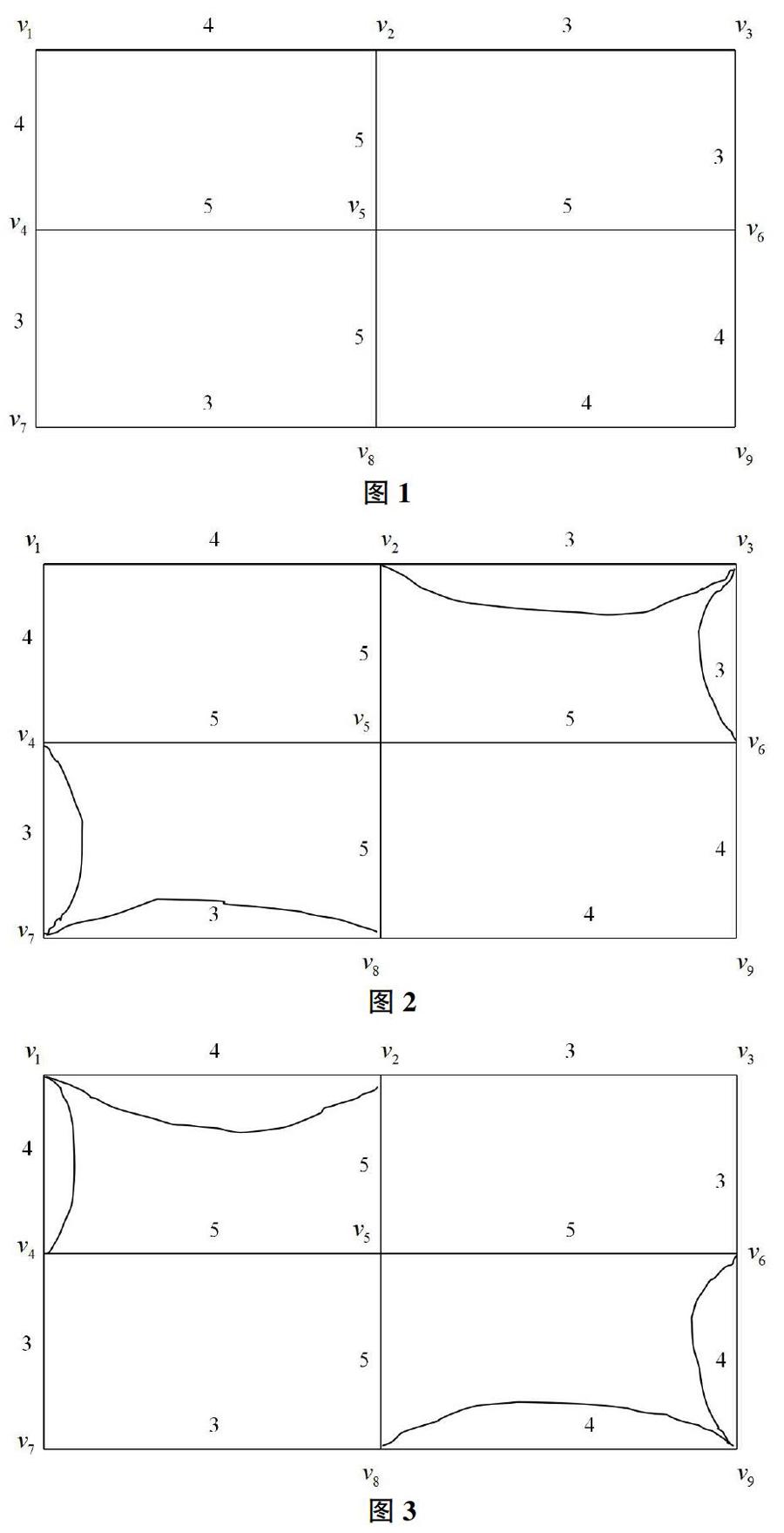
國內許多教材都出現了一處嚴重錯誤，以清華大學出版社的《運籌學》[1]為例，該教材（PP279-280）提出的奇偶點圖上作業法的最優性條件為：①在最優方案中，圖的每一條邊上最多有一條重復邊;②在最優方案中，圖中每個圈上的重復邊的總權不大于該圈總權的一半。這個最優性條件顯然存在嚴重錯誤。圖2和圖3都完全滿足上述最優性條件，兩個方案的權重不一樣，顯然它們不會都是最優方案，圖2的方案更優。

通過圖2和圖3的對比可以發現，這個“最優標準” 產生錯誤的原因是命題的大前提錯誤，也就是說，這個命題正確的大前提是奇點的配對方式正確。圖1共有v2、v4、v6、v8四個奇點，只有將v4和v8配對、v2和v6配對，才有可能尋找到最優方案，其它的兩種配對方式都無法得到最優解。

3? 中國郵遞員問題的指派問題模型與算法設計

根據奇偶點圖上作業法的思想，首先應該選擇正確的方式將所有奇點進行配對，重復配對的各對奇點間的最短路，就能得到最優方案。

解決最優配對的辦法可以用Dijkstra算法和指派問題的模型予以解決，具體算法如下（假設圖中共有n個奇點v1、v2、…、vn，n一定為偶數）：

①用Dijkstra算法求出圖中任意兩個奇點間的最短距離dij和最短路;

②構建指派問題的模型：

所以，將v2和v6配對、將v4和v8配對，重復配對的奇點間的最短路，即可得到圖2所示的最優方案。

參考文獻：

[1]《運籌學》教材編寫組.運籌學[M].三版.清華大學出版社，2005，6.

[2]管梅谷.關于中國郵遞員問題研究和發展的歷史回顧[J].運籌學學報，2015，9.

[3]馮俊文.中國郵遞員問題的整數規劃模型[J].系統管理學報，2010，12.

[4]李念祖.關于中國郵遞員問題的最優完全子圖算法[J].上海師范大學學報（自然科學版），2006，8.

[5]汪海森，林耿，卓彩娥.中國郵遞員問題的匹配算法[J].長江大學學報（自然科學版），2013，9.

[6]金毅.對“中國郵遞員問題”的數理分析[J].科技經濟市場，2009（03）.