立足教材 延伸課外
秦進 陳明 張少華 代姍妮 簡萱慧

基金項目:貴州省科學技術(shù)基金項目(黔科合LH字(2015)7042號)。
摘要:教科書是根本,既要重視教材基本知識的普及,又要注重能力的提高,要對教材真正理解。本文從對教材的觀點認識、拓展內(nèi)容和思想延伸等幾個方面闡述了教材延伸是十分必要。
關(guān)鍵詞:教材;內(nèi)容;延伸
幾何內(nèi)容是中小學數(shù)學課程重要的組成部分,教育部于2001年7月正式頒布了《全日制義務教育階段數(shù)學課程標準》,在《標準》中將幾何作為重要的內(nèi)容列入到我國義務教育各階段的數(shù)學課程。義務教育階段七至九年級人教版、北師大版、華師大版等教科書中的幾何內(nèi)容比較接近,人教版安排在第四、第五、第六、第七、第十一章等共十三章。教科書中幾何內(nèi)容主要涉及圖形的認識初步、平面直角坐標系、勾股定理、投影與視圖等。教師應該站在高度來審視教材,根據(jù)課程的需求對教材進行分析,特別是對教材深入理解認識,延伸拓展。以知識重構(gòu)為切入點,體驗學習數(shù)學內(nèi)容的過程,運用“高觀點”分析和處理中學數(shù)學問題,有利于提升教師的專業(yè)能力。
一、 觀點認識
人教版教科書是按照“簡單說理”“說理”“推理”“用符號表示推理”等不同層次,分階段逐步加深安排的。通過活動認識圖形,十分重視學生的動手操作和參與,教育部審定(2013)人教版教科書七年級上第四章圖形的初步認識,注重利用實物和幾何模型進行教學,采用實物入手,展示多彩的圖形世界與幾何知識的密切聯(lián)系,第119頁,筆尖可以看作一個點,這個點在紙上運動時形成線,節(jié)日的焰火也可以看成有點運動而成的,筆尖作為一個點運動成圓(圖1),汽車雨刮器在擋風玻璃上畫一個扇面(圖2)。點動成線,線動成面的角度進一步認識幾何基本圖形,幾何圖形可看成是點的集合點,幾何圖形也可以理解為由線組成,點和線兩者是相互對應的,點為元素的幾何觀點和線為元素的幾何觀點是統(tǒng)一的。平面可以看成點為元素的集合,也可以看成直線為元素的集合;圓可以看成由點構(gòu)成,也可以看成由直線構(gòu)成,如圖3所示,線包絡(luò)成圓。可以以點為元素來表達幾何對象,事實上,我們完全可以以直線為元素來表達幾何對象,幾何圖形看成是直線的集合。
1831年,普呂克在《解析幾何論》第二部分所述,將點坐標與線坐標進行類比“對偶”的方法建立解析幾何結(jié)構(gòu),線幾何的觀點在射影幾何中體現(xiàn)十分顯著。點和直線的地位是平等!點有方程,直線有坐標。平面可以看成直線為元素組成;錐面是由一簇直線構(gòu)成;單葉雙曲面、拋物雙曲面以及柱面等直紋面實質(zhì)上是由直線運動生成的曲面;二次曲線看作點的軌跡,也可以看作直線的包絡(luò)。《普通高中數(shù)學課程標準(實驗)》(蘇教版)選修21中“探究·拓展”內(nèi)容就體現(xiàn)了線幾何的觀點,引進齊次線坐標,打破了中學解析幾何點與數(shù)組一一對應的坐標觀點,將以點為基本元素的點幾何學轉(zhuǎn)化為直線為元素的幾何學。平面上的基本元素直線與點,它們之間的關(guān)系是結(jié)合關(guān)系。滿足三元二次方程的點集合稱為二次曲線(二階曲線),滿足三元二次方程的直線集合稱為二次曲線(二曲級線),二次曲線是成射影對應的點列對應點的聯(lián)線的集合。這樣高度概括的認識,抓住事物的本質(zhì),體會數(shù)學的觀點,打開認識的視野。
二、 思想延伸
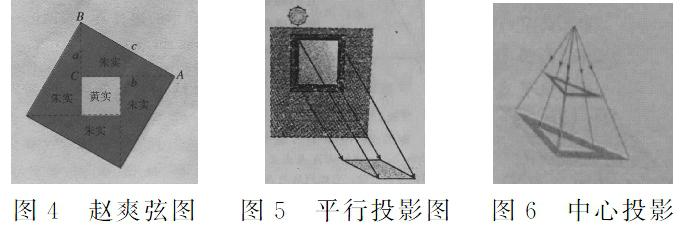
從數(shù)學文化的角度來說,培養(yǎng)數(shù)學的思想和方法是極為重要的。變與不變的數(shù)學思想和方法就是其中之一,可以說它貫穿義務教育階段教科書的始終。教育部審定(2013)人教版教科書八年級下第十七章勾股定理,趙爽弦圖(圖4),趙爽根據(jù)此圖指出:四個全等的直角三角形(紅色)可以圍成一個大的正方形,中空部分是個小正方形(黃色),通過對圖形的切割,拼接,巧妙利用面積關(guān)系證明了勾股定理.所謂的“出入相補”原理。此方法嚴謹而簡潔,這種證明的方法被一些數(shù)學家稱為“最省力的證法”,證明過程顯示了圖形間的相互關(guān)系,特別是體現(xiàn)了變與不變的數(shù)學思想。劉徽注《九章算術(shù)》時,也給了證明,留下注文:“勾自乘為朱方,股自乘為青方,令出入相補,各從其類,因就其余不移動也,合成弦之冪,開方除之,即弦也。”由于劉徽使用的弦圖已經(jīng)失傳,后世數(shù)學家只能根據(jù)這段注文進行多種解釋與推測,清代數(shù)學家李潢的補圖簡單明了,接近劉徽之意。“出入相補,各從其類”,這個原理是說一個平面圖形從一處移到另一處,面積不變,形狀可能發(fā)生變化,體現(xiàn)了變與不變的數(shù)學思想。縱觀勾股定理證明的歐幾里得證明、美國總統(tǒng)Garfield證明、辛卜松證明、梅文鼎證明、楊作玫證明、李銳證明等近20種方法都體現(xiàn)了變與不變的數(shù)學思想。
幾何變換用近代數(shù)學的觀點來看就是“幾何運算”,幾何變換把一個幾何圖形變?yōu)榱硪粋€幾何圖形,什么變了?什么沒有變?共同的屬性是變中有不變!教科書九年級下第二十九章投影,涉及平行投影與中心投影等。陽光透過長方形玻璃窗平行投影到地面上,地面上出現(xiàn)一個明亮的四邊形(如圖5),我們應該關(guān)注這個幾何變換中的不變量與不變性質(zhì);如圖6,此中心投影將三角形變?yōu)槿切危螤顩]有發(fā)生變化,三角形還是三角形,但是三角形的角的大小,邊的長度可能發(fā)生變化了。用變換群去研究相應的幾何學,闡述了幾何學的本質(zhì)是變中有不變,既要抓不變量與不變性質(zhì)的“不變”,又要抓量與性質(zhì)的“變”。多邊形的內(nèi)角和與邊數(shù)有關(guān),而多邊形的外角和恒等于360度;又如,等底等高的兩個三角形面積相等;等腰三角形底邊上一點到兩腰的距離之和是常數(shù)(定值)等等均蘊含變與不變的數(shù)學思想。
三、 內(nèi)容拓展
人教版教科書第二十四章圓安排了探索四點共圓的條件,利用探究過程,歸納出證明四點共圓的方法主要有四種:一是如果四點到一定點的距離相等,那么這四點共圓;二是四邊形的一組對角互補,那么這四邊形的四個頂點共圓;三是如果四邊形的一個外角等于它的內(nèi)對角,那么這四邊形的四個頂點共圓;四是如果兩個三角形有公共邊,公共邊所對的角相等,且在公共邊的同側(cè)兩個三角形的四個頂點共圓,通過實踐探索對教材內(nèi)容進行拓展。
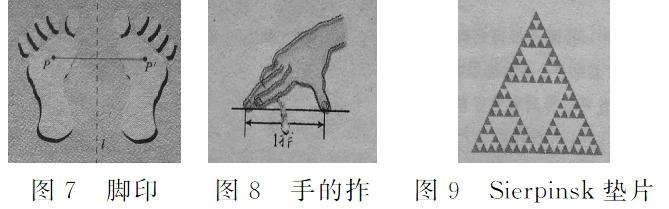
第十三章中的軸對稱中的最短路線問題,可以延伸到作圖問題,拓展到對稱變換、平移變換以及旋轉(zhuǎn)變換等進行理解,體會對應點、對應線段、對應圖形之間的關(guān)系。如圖7,左腳印和右腳印中鏈接一對對應點的線段被對稱軸垂直平分。可以理解為右腳印可以通過左腳印經(jīng)過對稱變換得到的。其中,P點變?yōu)镻′,這一對應點連線段被l平分。第二十七章相似中涉及長度的測量,測量離不開單位。測量長度的常用工具有游標卡尺、鋼卷尺、木尺等,如果測量的精度要求不高,可以用步長、肘、拃(如圖8)來測量距離。測量依賴于測量工具,歸根結(jié)底緊緊依賴于單位!數(shù)軸的三要素坐標原點、正方向以及長度單位,單位取得不一樣,坐標不一樣,直角坐標系亦如此。直角坐標系經(jīng)過仿射變換后得到新的坐標系——仿射射坐標系的x軸與y軸的單位長度也未必一樣。把一個正三角形分為全等的四個小正三角形,去掉中間一個正三角形,對剩下的3個小正三角形再分別重復以上做法……將這種做法繼續(xù)下去,就能得到小格子越來越多謝爾賓斯基地毯(如圖9)。這個圖的大大小小的三角形之間關(guān)系是相似,局部與整體之間是自相似的關(guān)系。
圖7腳印圖8手的拃圖9Sierpinsk墊片
這種現(xiàn)象廣泛存在,自然界大多數(shù)的圖形都是十分復雜而且不規(guī)則的。例如,海岸線、樹木、閃電、海浪等等,它們在歐氏幾何領(lǐng)域不可度量,而分數(shù)維恰好反映了這種不規(guī)則性和復雜性。從傳統(tǒng)的幾何學出發(fā),用什么樣的尺子都很難測量很復雜的幾何對象。從分形幾何學出發(fā),我們用一個看起來很復雜的測量單位去測量幾何對象,所得的結(jié)果卻十分簡單。
用好教材,必須真正理解教材,把握內(nèi)容之間的聯(lián)系,從另外一個視角來審視教材,注重觀點認識、拓展內(nèi)容和思想延伸顯得尤為必要。
參考文獻:
[1]義務教育教科書.數(shù)學(7~9年級)[M].北京:人民教育出版社,2014.
[2]梅向明.高等幾何[M].北京:高等教育出版社,1983.
[3]羅崇善.編寫國家級重點教材《高等幾何》的思考[J].四川師范大學學報(自然科學),2000(11).
[4]朱德祥.高等幾何[M].北京:高等教育出版社,1992.
[5]秦進.圓錐曲線的線幾何觀點認識法[J].中學數(shù)學教學參考,2014(11):54-55.
[6]秦進.圓錐曲線的中心射影認識法[J].中學數(shù)學教學參考,2014(10):40-41.
[7]秦進.高等幾何課程教學的認識與實踐[J].遵義師范學院學報,2017(4):108-110.
作者簡介:
秦進,陳明,張少華,代姍妮,貴州省遵義市,遵義師范學院;
簡萱慧,貴州省遵義市,遵義市第十六中學。

