近場動力學方法在邊坡穩定性分析中的應用

廖 洋，劉立勝，2，劉齊文，賴 欣，池晴佳，邵愛軍

(1.武漢理工大學力學系，湖北 武漢 430070；2.武漢理工大學材料復合新技術國家重點實驗室，湖北 武漢 430070；3.湖北省江漢運河航道管理處，湖北 武漢 430032)

邊坡的穩定性分析在邊坡防護以及施工安全等方面具有重要的意義[1-2]。傳統的邊坡穩定性分析一般采用極限平衡法[3-5]和有限元強度折減法[6-8]。極限平衡法在工程中有著廣泛的應用，但是由于其引入了條間力關系假設來消除邊坡穩定問題的靜不定性，故只能得到特定條件下單一的邊坡安全系數。一般情況下，極限平衡法得到的既不是上限解也不是下限解。不同于極限平衡法僅對邊坡的宏觀安全特性進行描述，有限元方法通過借助強度折減技術，不僅能得到邊坡土體的應力及變形分布規律，還可以得到邊坡的安全系數，以及邊坡失穩時的塑性屈服面，即邊坡滑移面。有限元強度折減法在計算邊坡穩定性問題時考慮了邊坡土體的非線性本構關系、復雜的載荷，甚至整個施工過程，能夠較為真實地反映邊坡土體的應力、變形隨時間的變化情況。

近場動力學方法是Silling等[9-10]提出的一種基于非局域平均思想的一類微分-積分方法，其在處理裂紋、滑移等不連續問題方面具有較好的適應性。起初的近場動力學方法是一種基于鍵的非局域方法，比較簡單，只能模擬簡單的本構關系；其后提出的基于非常規態的近場動力學方法通過引入矩量法[11]，可以得到質點的任意時刻的變形梯度以及應變。基于非常規態的近場動力學方法[12-15]作為一種非局域的無網格粒子類方法，不僅具備有限元方法的優點，而且在計算非線性問題時還具有更好的收斂性以及對不連續問題的適用性。當邊坡處于臨界失穩狀態發生滑移時，有限元方法的計算容易出現不收斂現象，而近場動力學方法不僅能計算得到邊坡達到臨界狀態的收斂解，還能模擬邊坡的滑移過程。此外，基于非常規態的近場動力學方法可以用來實現土體的非線性本構模型，如Drucker-Prager屈服模型、摩爾-庫侖屈服模型等。本課題組在土體的爆炸[16]以及邊坡穩定性分析[17]方面已做了一些探索性的工作。在此基礎上，本文基于摩爾-庫侖屈服準則以及非關聯流動法則，利用近場動力學強度折減法對引江濟漢工程中出口船閘的基坑邊坡的穩定性進行了分析。

1 近場動力學強度折減法

1. 1 基于非常規態的近場動力學方法

在基于非常規態的近場動力學方法中，某一質點的變形狀態與其自身和鄰域內其他質點的位移差有關。任意質點i與其鄰域內質點j之間的相互作用力被稱作力態，分別為T和T′。

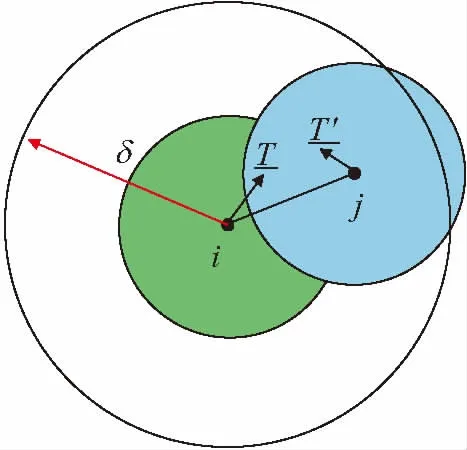
圖1 基于非常規態的近場動力學方法中質點及其鄰域Fig.1 Particle in non-ordinary state-based peridynamics and its neighbourhood

任意質點i的變形梯度張量F，可由下式計算:

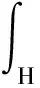
(1)

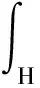
(2)

式中：Y為質點i與j之間的變形后的相對位置矢量;X為質點i與j之間的初始相對位置矢量;V′為質點j的體積;K為質點i的形狀張量;w(|X|)為質點j的影響函數;H為質點i的鄰域范圍。

根據連續介質力學理論，物質體在時間步n+1的形態Yn+1可由前一時間步n的形態Yn計算得到:

Yn+1=Yn+Δu

(3)

式中：Δu為當前時間步n的位移增量。

因此，從時間步n到n+1的變形梯度增量G的計算公式為

G=F··F-1

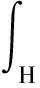
(4)

式中：F·為變形梯度F的時間導數，即速度梯度。

物質體的運動可以分為應變增量和剛體轉動增量兩部分：

γ=(G+GT)/2

ω=(G-GT)/2

(5)

式中：γ為應變增量;ω為剛體轉動增量。

因此，有效應力增量Δσ可通過彈性矩陣De與應變增量γ進行縮并計算得到：

Δσ=De∶γ

(6)

根據Hughes-Winget理論[18]，質點當前時刻n+1的柯西應力張量，可由下式計算:

σn+1=σ∧n+Δσ

(7)

σ∧n=RT·σn·R

(8)

其中，σn為時刻n的應力狀態；σ∧n為σn從時刻n到時刻n+1發生剛體轉動的結果;R為轉動張量，可以由下式計算：

R=I+(I-0.5ω)-1·ω

(9)

式中：I為二階單位張量。

根據柯西應力張量σn+1，可計算求得第一類皮奧拉-基爾霍夫非對稱應力張量Pn+1：

Pn+1=Jσn+1F-T

(10)

式中：J為變形梯度F的行列式。

力態T和T′的計算形式如下：

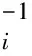
(11)

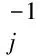
(12)

基于非常規態的近場動力學運動平衡方程為

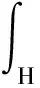
(13)

式中：ü為質點i在t時刻的位移二階導數，即加速度；x為質點i的初始坐標；ρ為質點的材料密度；b為質點i在t時刻受到的外力矢量作用。

根據基于非常規態的近場動力學運動平衡方程，可計算得到質點i當前時刻n的加速度，最后使用歐拉法、蛙跳法或Velocity-Verlet積分法，可求得下一時刻的質點位移，從而完成變形體的狀態更新。

1. 2 強度折減法

強度折減法的基本原理是通過不斷減小材料的強度參數直到邊坡開始出現失穩。邊坡失穩臨界狀態所對應的折減系數即是該邊坡的安全系數，則有

ct=cini/FOS

(14)

tanφt=tanφini/FOS

(15)

式中：FOS為折減系數；ct和φt分別為邊坡臨界狀態的內聚力和內摩擦角；cini和φini分別為邊坡初始狀態的內聚力和內摩擦角。

在有限元強度折減法中，當材料強度進行折減后，若有限元計算收斂，則認為邊坡是穩定的；當材料強度折減到一定范圍時，有限元計算開始出現不收斂的現象，此時的折減系數一般視作邊坡的安全系數。

在近場動力學中引入強度折減法，其基本的計算思想與有限元法相同；不同之處是，近場動力學方法是以邊坡系統的最大位移作為判斷依據，當邊坡處于穩定狀態時，不同折減系數下邊坡的最大位移值基本不變，一旦邊坡失穩，邊坡的最大位移值會發生較大的變化。因此，通過觀察邊坡最大位移值的變化，可以在近場動力學強度折減法中捕捉到邊坡的安全系數。

2 摩爾-庫侖屈服準則與非關聯流動法則

2. 1 摩爾-庫侖屈服準則

摩爾-庫侖屈服準則常被用作混凝土以及巖土類材料的塑性判據。對于平面應變問題[19]，摩爾-庫侖準則可表示為

F=-[2ccosφ-(σx+σy)sinφ]2+(σx-σy)2+(2τxy)2=0

(16)

式中：c和φ分別為土體的內聚力和內摩擦角，σx、σy和τxy為應力分量。

對摩爾-庫侖屈服準則進行線性化處理[20],令X=σx-σy,Y=2τxy,R=2ccosφ-(σx+σy)cosφ，在XOY坐標系中，屈服函數可表示成一個圓，可以使用外接多邊形進行逼近。當多邊形邊數為p時，線性化后的屈服函數為

F=Mkσx+Nkσy+Pkτxy-2ccosφ

(17)

其中:

Mk=cosαk+sinφ

Nk=sinφ-cosαk

Pk=2sinαk

αk=2πk/p(k=1,2,…,p)

(18)

2. 2 基于非關聯流動法則的彈塑性矩陣

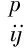
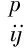
(19)

式中：dλ為塑性應變增量的大小，它是一個非負的標量；Q為塑性勢函數；σij為應力張量。

在非關聯流動法則中，塑性勢函數Q與屈服函數F不相等，即Q≠F。對于理想的彈塑性材料，硬化參數A為零，則應力-應變增量表達式為

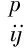
(20)

式中：dεij為總的應變增量;Dep為彈塑性矩陣;De、Dp為塑性矩陣，其形式[21]如下:

Dp=?F?σTDe·De?Q?σ?F?σTDe?Q?σ

(21)

2. 3 基于摩爾-庫侖屈服準則的應力更新

若屈服函數F<0，則材料處于彈性階段，只需根據近場動力學的一般計算流程更新應力即可；若屈服函數F≥0，則材料發生了塑性變形，此時首先需要根據公式(20)和(21)計算出當前的彈塑性矩陣Dep，用以代替公式(6)中的彈性矩陣De，其應力增量為

Δσ=Dep∶γ

(22)

3 工程實例應用與分析

本文以引江濟漢工程邊坡為例，基于摩爾-庫侖屈服準則以及非關聯流動法則，利用近場動力學強度折減法對引江濟漢工程中出口船閘的基坑邊坡穩定性進行了分析。引江濟漢工程出口船閘位于潛江市高石碑鎮，閘址區地形平坦，地面高程為32.5 m。

3. 1 地層結構分布

該地區的地層結構分布如下：①亞砂土，結構松散—較密實，不均質，砂感明顯，黏性差，厚度為0～2.1 m，底板高程為29.8～31.0 m；②亞黏土，可塑—軟塑，黏性較強，厚度為0～2.7 m，底板高程為26.06～27.63 m；③黏土，可塑為主，局部硬塑，土質均一細膩，黏性強，厚度為6.2～16.2 m，底板高程為8.6～11.5 m；④粉細砂，飽和，稍密—中密，厚度為2.6～11.5 m。

3. 2 邊坡土質及計算模型

基坑邊坡地層上部為亞黏土、亞砂土、黏土，局部為淤泥質土，中下部為細砂，邊坡土體較軟弱。閘址地面的高程為32.5 m，最大開挖深度約17 m，邊坡比取值范圍為1∶2～1∶2.5。邊坡土質分層情況以及邊坡尺寸見圖2，邊坡土體近場動力學計算模型見圖3，邊坡土體的材料參數見表1。

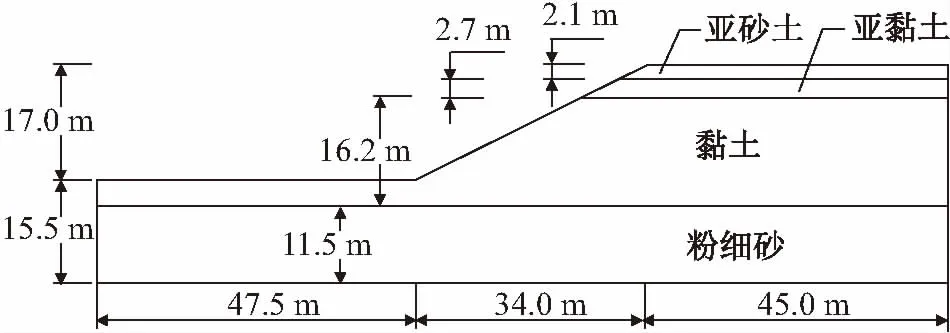
圖2 邊坡土質分層情況以及邊坡比為1∶2時的尺寸圖Fig.2 Soil layers and size of the slope when the slope ratio is 1∶2

圖3 邊坡土體的近場動力學計算模型圖Fig.3 Peridynamic model of the slope

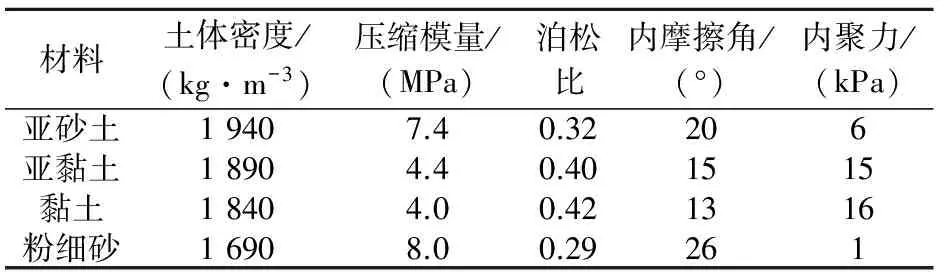
材料土體密度/(kg·m-3)壓縮模量/(MPa)泊松比內摩擦角/(°)內聚力/(kPa)亞砂土19407．40．32206亞黏土18904．40．401515黏土18404．00．421316粉細砂16908．00．29261

3. 3 計算結果與分析

保持基坑的開挖深度不變，為17.0 m，將邊坡比分為1∶2和1∶2.5兩種工況，使用強度折減法針對不同的折減系數FOS(1.00、1.15、1.25、1.35、1.50)分別計算得到了邊坡的最大位移以及邊坡的塑性應變分布情況,見圖4、圖5和圖6。

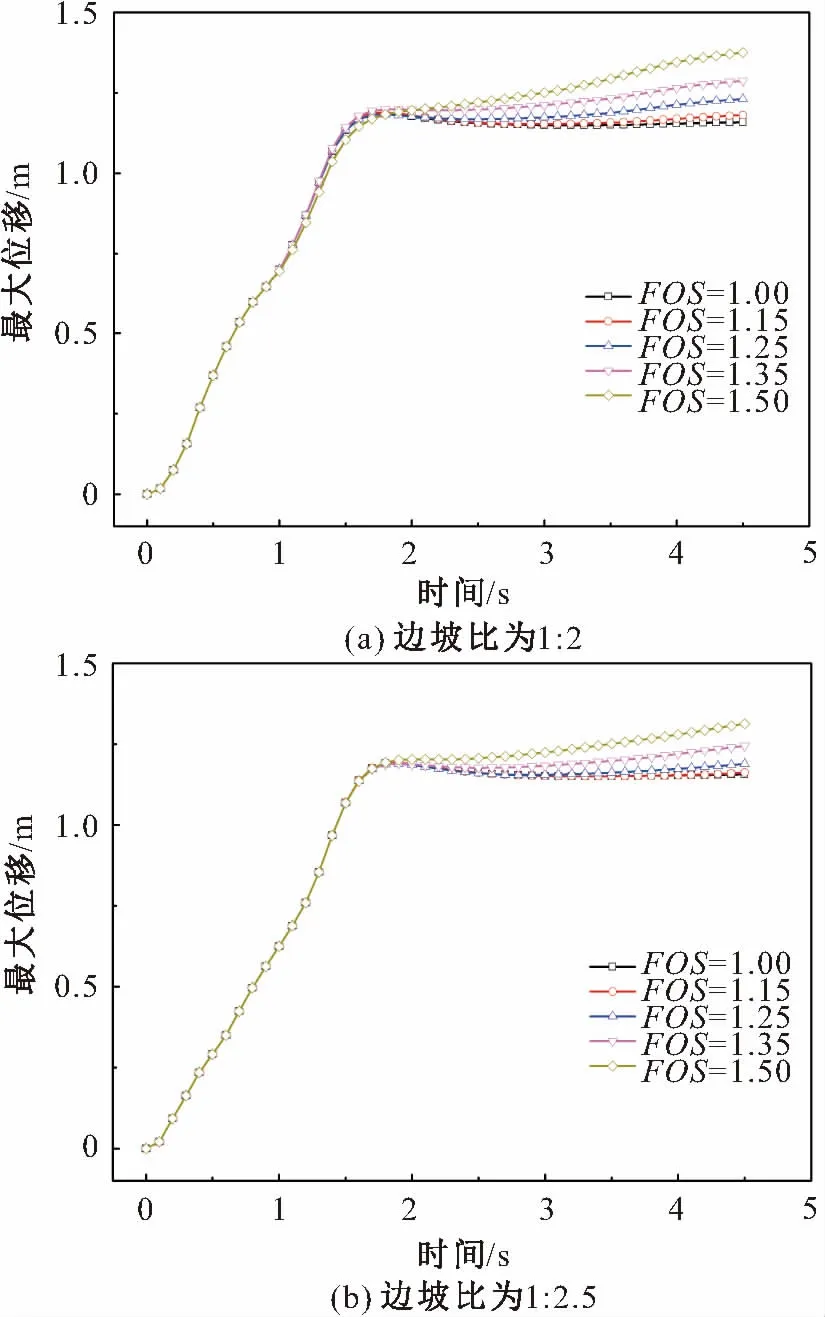
圖4 不同折減系數對應的邊坡最大位移曲線Fig.4 Maximum displacements of the slope corresponding to different reduction factors

由圖4(a)可見，對于邊坡比為1∶2的邊坡土體，當折減系數(FOS)為1.15時，邊坡最大位移曲線就已經出現了不收斂，因此可以認為此時邊坡的安全系數小于1.15。由圖4(b)可見，對于邊坡比為1∶2.5的邊坡土體，當折減系數為1.15時，邊坡最大位移曲線仍然是收斂的，但當折減系數為1.25時，邊坡最大位移曲線出現了不收斂，因此可以認為此時邊坡的安全系數小于1.25。

從以上計算結果來看，邊坡的安全系數較低，邊坡土體極容易發生失穩，因此可以進一步分析邊坡的塑性屈服區域以及最大水平位移出現的區域。

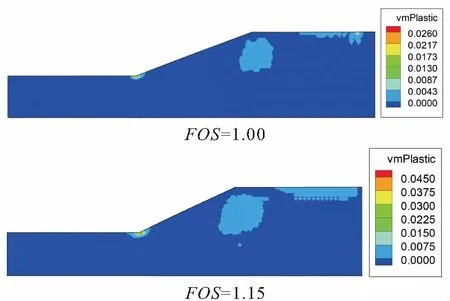
圖5 邊坡比為1∶2、t=4.5 s時邊坡的塑性屈服區域 分布圖Fig.5 Plastic yield region of the slope when the slope ratio is 1∶2.5 and t=4.5 s

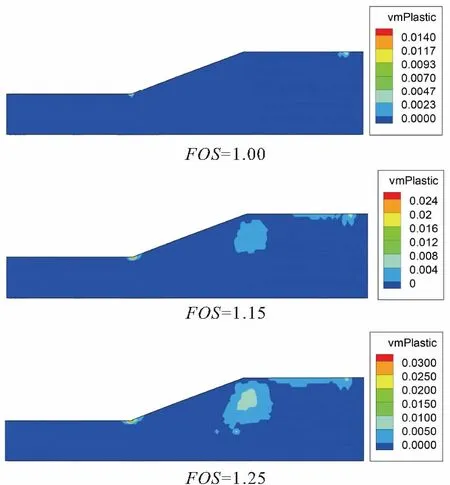
圖6 邊坡比為1∶2.5、t=4.5 s時邊坡的塑性屈服區域 分布圖Fig.6 Plastic yield region of the slope when the slope ratio is 1∶2.5 and t=4.5 s

由圖5可見，當折減系數為1.00時，邊坡坡腳就開始出現了塑性屈服區域，且隨著折減系數的增加，坡腳的塑性屈服區域急劇增大，同時邊坡上部也開始出現塑性屈服區域。對比圖5和圖6可見，隨著邊坡比的增大，邊坡坡腳的塑性屈服區域明顯減小，但是邊坡的穩定性仍然較差，此時應加強坡腳的防護，這一結論與實際施工的情況是符合的。

當邊坡比為1∶2或1∶2.5時，對于不同的折減系數，邊坡的水平位移分布趨勢基本相同，圖7給出了邊坡比為1∶2、折減系數為1.0時邊坡的水平位移分布圖，圖8給出了不同邊坡比情況下邊坡最大水平位移隨折減系數的變化曲線。

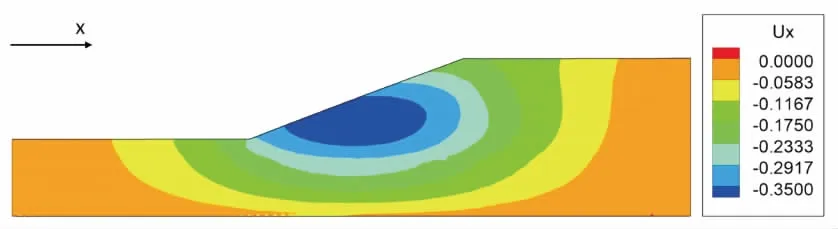
圖7 邊坡比為1∶2、FOS=1.0時邊坡的水平位移 分布圖Fig.7 Horizontal displacement when the slope ratio is 1∶2 and FOS=1.0

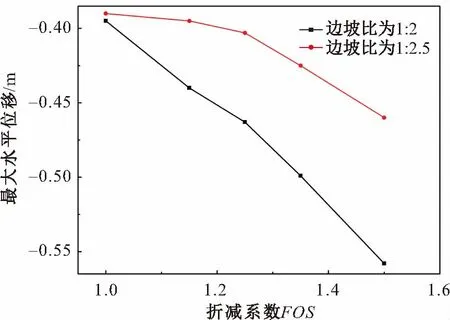
圖8 不同邊坡比情況下邊坡最大水平位移隨折減 系數的變化曲線Fig.8 Maximum horizontal displacement of the slope with the reduction factor under different slope ratios

由圖7和圖8可見，邊坡的最大水平位移出現在坡腳的上端，且隨著邊坡比的增大，邊坡的最大水平位移明顯減小，邊坡趨于穩定。

4 結 論

通過上述工程實例計算與應用，可得到如下結論：

(1) 本文所提出的基于摩爾-庫侖屈服準則的近場動力學方法可以用于描述邊坡土體材料的力學行為。

(2) 基于非常規態的近場動力學強度折減法可以用于邊坡的穩定性分析，所得到的計算結果與實際施工情況是一致的。

[1] 楊茜,陳勝,朱桂春.基于拉格朗日乘數法的邊坡穩定性變分法[J].安全與環境工程,2010,17(4):111-113.

[2] 郭利娜,胡斌,胡啟晨.基于Geo Slope軟件對青蓮寺邊坡的穩定性分析[J].安全與環境工程,2011,18(6):20-24.

[3] 朱大勇,盧坤林,臺佳佳,等.基于數值應力場的極限平衡法及其工程應用[J].巖石力學與工程學報,2009,28(10):1969-1975.

[4] 孫聰,李春光,鄭宏.基于整體穩定性分析法的邊坡臨界滑動面搜索[J].巖土力學,2013,34(9):2583-2588.

[5] 欒茂田,金崇磐,林皋.土體穩定分析極限平衡法改進及其應用[J].巖土工程學報,1992,14(S1):20-29.

[6] 張坤勇,李廣山,李旺林,等.南水北調南干渠邊坡有限元穩定性分析[J].河北工程大學學報(自然科學版),2016,33(4):27-32.

[7] 趙尚毅,鄭穎人,時衛民,等.用有限元強度折減法求邊坡穩定安全系數[J].巖土工程學報,2002,24(3):343-346.

[8] 李垠,蘇凱,李杰.Mohr-Coulomb等面積圓屈服準則在邊坡穩定分析中的應用[J].大地測量與地球動力學,2009,29(1):135-139.

[9] Silling S A.Reformulation of elasticity theory for discontinuities and long-range forces[J].JournaloftheMechanics&PhysicsofSolids,2000,48(1):175-209.

[10]Silling S A,Epton M,Weckner O,et al.Peridynamic states and constitutive modeling[J].JournalofElasticity,2007,88(2):151-184.

[11]Li S,Qian D,Liu W K,et al.A meshfree contact-detection algorithm[J].ComputerMethodsinAppliedMechanics&Engineering,2001,190(24/25):3271-3292.

[12]Zhou X,Wang Y,Xu X.Numerical simulation of initiation,propagation and coalescence of cracks using the non-ordinary state-based peridynamics[J].InternationalJournalofFracture,2016,201(2):213-234.

[13]Kilic B,Agwai A,Madenci E.Peridynamic theory for progressive damage prediction in center-cracked composite laminates[J].CompositeStructures,2009,90(2):141-151.

[14]Amani J,Oterkus E,Areias P,et al.A non-ordinary state-based peridynamics formulation for thermoplastic fracture[J].InternationalJournalofImpactEngineering,2016,87:83-94.

[15]黃丹,章青,喬丕忠,等.近場動力學方法及其應用[J].力學進展,2010,40(4):448-459.

[16]Lai X,Ren B,Fan H,et al.Peridynamics simulations of geomaterial fragmentation by impulse loads[J].InternationalJournalforNumerical&AnalyticalMethodsinGeomechanics,2015,39(12):1304-1330.

[17]Lai X,Liu L S,Liu Q W,et al.Slope stability analysis by peridynamic theory[J].AppliedMechanics&Materials,2015,744/745/746:584-588.

[18]Hughes T J R,Winget J.Finite rotation effects in numerical integration of rate constitutive equations arising in large-deformation analysis[J].InternationalJournalforNumericalMethodsinEngineering,1980,15(12):1862-1867.

[19]孫聰,李春光,鄭宏,等.基于四邊形網格的邊坡上限有限元法[J].巖石力學與工程學報,2015,34(1):114-120.

[20]Lyamin A V,Sloan S W.Upper bound limit analysis using linear finite elements and non-linear programming[J].InternationalJournalforNumerical&AnalyticalMethodsinGeomechanics,2002,26(2):61-77.

[21]張魯渝,劉東升,時衛民.擴展廣義Drucker-Prager屈服準則在邊坡穩定分析中的應用[J].巖土工程學報,2003,25(2):216-219.