一種基于全局K-均值聚類的改進算法

李燕梅

（滇西科技師范學院，云南 臨滄 677000）

1 引言

K-均值聚類算法通過迭代算法來解決實際應用中出現的聚類問題，并得出聚類誤差的最優解，被廣泛應用于聚類誤差問題中。K-均值聚類算法采用隨機的方式選擇K個對象作為初始聚類中心，通過迭代算法降低聚類誤差以達到改變聚類中心的目的，屬于一種基于中心點的基礎聚類算法。K-均值聚類算法的弊端在于選取初始聚類中心點相對慎重，進而影響了算法的效率。為得到K-均值聚類算法中聚類誤差的近似最優解，需要合理安全初始聚類中心點的位置，確保每個聚類中心點之間存有差異。針對K-均值聚類算法面臨的問題，專家學者不斷深入研究，以期通過新型算法達到全局最優化的目的。但目前采取遺傳算法、模擬算法等技術來解決該問題還存在一定的漏洞，適用性不強，導致認可度不高。因此，在解決實際問題中使用度最高的聚類算法還是K-均值聚類算法。本文提出基于K-中心點算法的改進思想，將其作為全局K-均值聚類算法的初始聚類中心，最后實現聚類時間短、魯棒性強的目標。

2 K-均值聚類算法

K-均值聚類算法用于解決數據聚類問題，由麥克奎因首次提出。K-均值聚類算法具有算法簡單、計算速度快的優勢，廣泛應用于工業、科技等領域。K-均值聚類算法處理了含有n個數據點集合如X={x1，x2，…，xn}中需要劃分出以K為對象的Cj類簇問題，其中j=1，2，…k。K-均值聚類算法的步驟為：隨機選取K個對象作為初始聚類中心，然后計算每個數據點與各個聚類中心之間的距離，并將數據點劃分至距離最近的聚類中心內，以此形成K個初始聚類。對初始聚類中心根據聚類中現有的數據點重新計算，采用迭代算法進行劃分，當聚類中心數值不再變化時，說明所有K數據對象已全部劃分完畢，進而進行聚類準則函數收斂，如若數值還處于變化，則需要繼續采用迭代算法劃分，直至成功。K-均值聚類算法需要注意使用迭代算法時是對全部數據點進行分配，沒有進入聚類中心的數據點在下次迭代過程中仍參與分配。當聚類中心不再變化后，說明聚類準則函數收斂完畢，K-均值聚類算法結束。

3 全局K-均值聚類算法

全局K-均值聚類算法是給定含有n個數據點集合如X={x1，x2，…，xn}，以期將其劃分為以K為對象的Cj類簇問題，其中j=1，2，…k，全局K-均值聚類算法具有全局最優算法的優勢，無須依托于初始因素，提高了算法的確定性。全局K-均值聚類算法中的局域搜索程序采用K-均值聚類算法，全局K-均值聚類算法采用最優化方式在算法運行各個階段添加新的聚類中心，聚類中心的初始值也不再隨機選取。

針對實際應用環節中出現的K個簇聚類問題，全局K-均值聚類算法的步驟如下：將簇中心的最優位置確定為數據集的質心以此解決一個簇的聚類問題，以此類推，解決n個簇的聚類問題是執行n次全局K-均值聚類算法，明確簇的中心初始位置即可。當K-1為第一個聚類中心的最優解位置時，將x數據點作為第二個簇的初始聚類中心，i=1,2,...,n，運用全局K-均值聚類算法解決n次聚類問題后，得出K-2時的聚類問題解決方法為最優解。由此可知，使用全局K-均值聚類算法時，當我們得出（K-1）聚類問題的解決方法時，可以采用類似步驟解決K-均值聚類算法的問題。針對n次對應以K為對象的類簇問題，執行K-均值聚類算法，明確初始簇聚類中心，得出聚類問題的最優解。基于全局K-均值聚類算法的步驟，最終可以得出K個聚類問題的解決方式，當聚類數目小于K的聚類問題也可采用同類方式予以解決。

全局K-均值聚類算法的優勢在于確定類聚中心數目，為充分發揮出此優勢，需要有效解決各種簇數目的聚類問題，基于合理的準則來確定K值，不再隨機選擇K對象。因此，應用全局K-均值聚類算法可以排除初始類中心點對聚類算法結果造成的不良影響。但由于全局K-均值聚類算法中的全部K值都需要執行K均值算法，計算任務量大，所以多數使用者關心全局K-均值聚類算法應用是否過于復雜，因此在后續應用過程中改進該算法具有重要的作用。

4 基于全局K-均值聚類算法的改進

本文研究一種基于全局K-均值聚類算法的改進，首先需要對全局K-均值聚類算法進行有效掌握。其將K個聚類中心的問題轉化為從局域搜索初始狀態入手。當K=1時，增加一個聚類中心，需要用迭代算法求出K的聚類答案。全局K-均值聚類算法將K-1聚類質心作為默認樣本，將K-1的前一個聚類中心作為K-均值聚類算法的最佳初始位置，通過反復運行全局K-均值聚類算法來確定最佳的初始中心。

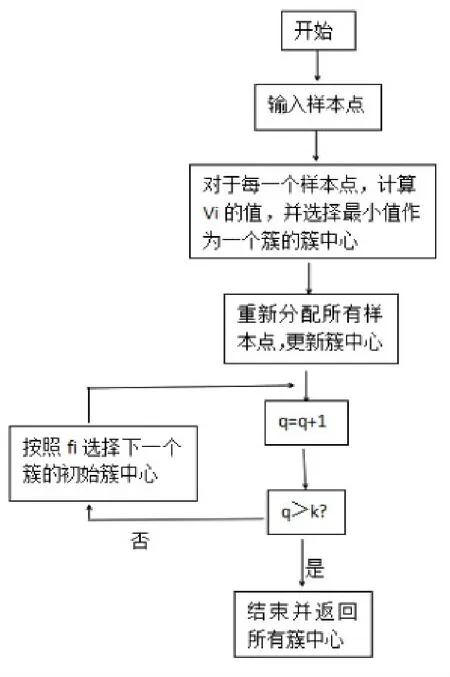
圖1 算法流程圖

本文基于全局K-均值聚類算法的算法思想，提出新的初始化方法，將K中心為初始中心的思想融入全局K-均值聚類算法中，來確定下一個聚類中心的初始中心，形成一種新型改進方法。改進后的全局K-均值聚類算法需要針對密集的樣本，找到距離現有簇中心較遠的簇作為樣本，并算出其最優初始中心，這樣有利于避免現有簇中心點的干擾，也可以彌補全局K-均值聚類算法計算量較大的弊端。改進后的全局K-均值聚類算法確定聚類中心的初始最優位置需要計算一個函數值，改變了中心選擇的方式，該算法選擇樣本分布密集，且距離現有簇中心較遠的簇作為樣本的最優初始位置選擇點，具有相對的科學合理性。距離過近的樣本簇在使用全局K-均值聚類算法時難免重復運算問題，造成運算結果準確性降低。對改進的全局K-均值聚類算法通過人工模擬數據和學習庫中的數據實驗測試，得出其相較于改進前算法具有聚類效率提升、誤差降低的優勢。

算法步驟如下：

第一步：針對樣本點xi，計算距離比Vi。中最小的點為xi，將其作為第一個簇的中心，并置q=1（q為簇中心數）；

第二步：針對簇中p=1,2,...,q,將xi，i=1,2,...,n劃分至最近的簇中，并更新簇中心為第i簇的樣本數，由此計算偏差

第三步：置q=q+1，當q＞k時，算法結束；

5 實驗與結果

通過以下隨機生成人工數據集來對改進全局K-均值聚類算法進行驗證，其中涵蓋噪音數據，以證明改進后全局K-均值聚類算法的抗干擾性能。將數據分為三類，各含有120個二維數據樣本，且滿足正態分布要求。第i類中橫坐標x的均值為縱坐標y的均值為第i類的標準差為在第二類數據中加入噪音點，其標準差為σ1。這三類隨機生成帶有噪音數據的參數如表1所示，樣本分布圖如圖2所示。

表1 隨機生成帶有噪音數據的參數

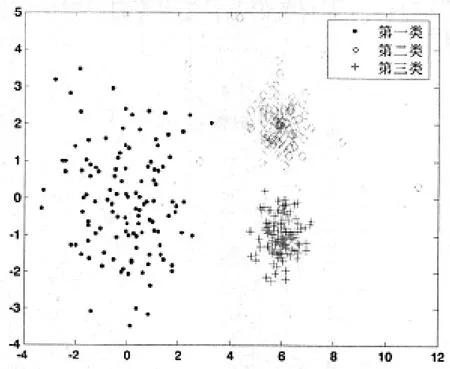
圖2 隨機生成的樣本分布

將全局K-均值聚類算法與改進后算法應用于三類隨機數據中，得出的聚類誤差平方和（E）和聚類時間（T）如表2所示，聚類結果圖如圖3所示。

表2 應用二種算法對隨機生成數據的聚類結果比較

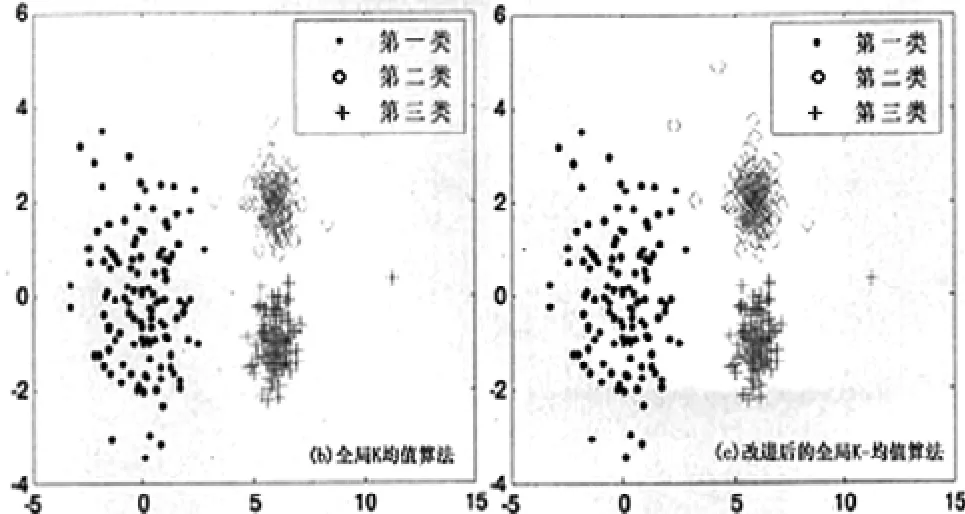
圖3 二種算法的聚類結果圖

由圖3可知，二種算法應用于三類隨機生成的帶有噪音點的數據中產生了類似的聚類效果，對比全局K-均值算法和改進后算法可知，本文中改進后的算法具有聚類時間短的優點，且改進后的全局K-均值算法基本不受噪音點的干擾。通過實驗可知，基于全局K-均值算法改進后的算法聚類效果良好，適合推廣應用。

[1]謝娟英，張琰，謝維信，等．一種新的密度加權粗糙K-均值聚類算法[J]．山東大學學報(理學版)，2010，45(7)：1-6．

[2]王軍敏，李艷．基于K均值算法的數據聚類和圖像分割研究[J]．平頂山學院學報，2014(2)：43-45．

[3]謝娟英，馬箐，謝維信．一種確定最佳聚類數的新算法[J]．陜西師范大學學報(自然科學版)，2012(1)：13-18．

[4]步媛媛，關忠仁．基于K-means聚類算法的研究[J]．西南民族學院學報(自然科學版)，2009，35(1)：198-200．

[5]吳景嵐朱文興．基于K中心點的文檔聚類算法[J]．蘭州大學學報(自然科版)，2005，41(5)：88-91．

[6]徐輝，李石君．一種整合粒子群優化和K-均值的數據聚類算法[J]．山西大學學報(自然科學版)，2011，34(4)：518-523．