散貨船配載儀中破艙穩性計算

沈 曄， 孫 霄 峰， 尹 勇， 劉 春 雷

( 大連海事大學 航海動態仿真和控制交通運輸行業重點實驗室， 遼寧 大連 116026 )

0 引 言

船舶在營運過程中一旦發生海損事故，艙室破損，極有可能造成船毀人亡的后果．為了減少這種風險，船舶在設計階段就應考慮破艙穩性的問題．船舶破艙穩性是指船舶在艙室破損的情況下維持一定的浮態和穩性，防止或延緩沉沒的一種能力，是船舶的重要性能．

傳統的散貨船破艙穩性計算基于船舶型值表或型線圖，主要有郭洛瓦諾夫法、克雷洛夫-達爾尼法等[1]．姜玲[2]采用二次開發技術，在SolidWorks 的基礎上，利用VB語言開發出一套破艙穩性計算程序；周瑞平等[3]使用B樣條函數對船舶型值表中的數據進行處理，使用VB.NET和Access數據庫開發出船舶穩性計算軟件；段興鋒[4]利用Access數據庫，以C++語言為開發工具，在MFC框架下開發出基于型值表的船舶裝載儀；蔡曉梅[5]利用Maxsurf軟件建立船體三維曲面模型，以此為數據來源進行破艙穩性計算；林焰等[6]用數據型值表描述船型，在水線面與船體表面求交時將坐標轉換，運用格林公式計算水線面下船體和艙室的特征參數；肖維維等[7]對比了表面元法和基于NURBS曲面的最優化方法在破艙穩性計算中的差異，指出了兩種方法存在的問題．

綜上所述，國內大部分配載儀的數據來源都是型值表以及型線圖或者在現有軟件的基礎上做二次開發．基于型值表或型線圖的破艙穩性計算存在很大誤差，尤其是運用于大角度傾斜下復雜船型破艙穩性的計算時誤差更大，并且在船型數據輸入模塊，用戶需要在型值表中讀取或在型線圖中量取大量描述船體的點坐標輸入到軟件中，十分費時費力．所以，將型值表或型線圖作為數據來源的破艙穩性計算已經不能滿足現代船舶設計的需要；而對現有的軟件做二次開發也需要先建立模型，精度往往很差．

為了解決散貨船配載儀中破艙穩性計算精度不高、操作復雜的問題，基于三維設計數據的破艙穩性計算法應運而生，國際上大部分知名配載儀軟件，例如NAPA[8]、Maxsurf[9]等均基于船舶的三維設計數據進行計算，具有實時、高效、精確等優點，但其高昂的價格卻是國內小型船舶公司承受不起的．而且由于商業保密的原因，這些軟件的計算方法尚未可知．

本文基于船舶三維設計數據用最小功法和靜平衡法進行散貨船破艙穩性的計算，比較并分析兩種方法的計算結果，并將精度較高的計算方法應用于散貨船配載儀中破艙穩性計算模塊．

1 船舶三維數據的獲取

三維方法計算破艙穩性需要確定船體和破損艙室的型值數據，本文規定沿船艏方向為x軸的正方向，y軸左舷方向為正，z軸垂直于基平面向上為正．沿船長方向，按照裝載手冊中的肋位以一定的間隔垂直于x軸對船體進行切片，得到每個切片處的船舶橫剖面型線數據，如圖1所示．為得到船舶外板數據，需要對所得的型線數據進行等距偏移，偏移量為船殼的平均板厚，具體的實現方法見文獻[10]．船艙型值數據的獲取與此類似，但是不需要對其進行等距偏移．通過以上的方法可以得到船體外表面以及各艙室內表面的三維數據．

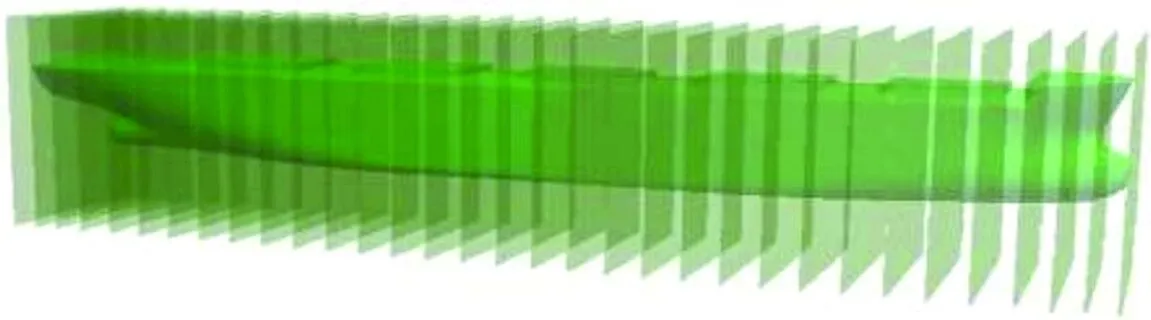
圖1 散貨船“RUI AN CHENG”型表面切片示意圖

2 破艙穩性計算

目前散貨船破艙穩性計算的方法主要有兩種：一種是基于最小功原理的自由縱傾法，該方法固定船舶的橫傾角，通過牛頓迭代法[11]或者優化法[12]求船舶達到特定橫傾角時的縱傾和吃水，然后基于最小功原理可以求得船舶破艙后的穩性力臂，從而可以獲得船舶的破艙穩性曲線；另一種是靜平衡下的自由縱傾法，該方法分析船舶傾斜時的受力平衡狀態，保證船舶橫傾到指定角度時船舶所受外力和外力矩為零．

2.1 基于最小功原理的自由縱傾法

船舶在自由傾斜時會逐漸到達位能最小的位置．船舶在初始浮態的基礎上橫傾至指定角度，利用最小功原理建立優化模型，使用解析優化算法算出當前橫傾角對應的穩性力臂．在相同載況下連續設定目標橫傾角，求得對應的穩性力臂，繪制出破艙穩性曲線．相關的實現方法見文獻[12]．

2.2 靜平衡下的自由縱傾法

為了方便計算，引入下列符號：

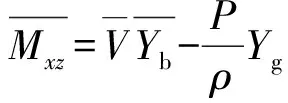
(1)

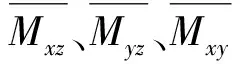
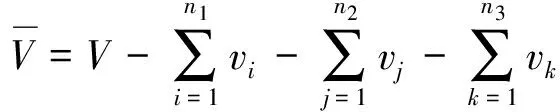
(2)

式中：n1、n2、n3分別為第1類、第2類、第3類破損艙室的總數；i、j、k分別為第1類、第2類、第3類破損艙室的編號，v、x、y、z分別為艙室進水體積和中心坐標；V、Xb、Yb、Zb為艙室破損后船體水下部分的體積和浮心坐標．以上數據可利用船舶吃水和橫傾角通過對船舶三維數據進行積分求解．

由文獻[13]可得破艙后的浮態平衡方程組：

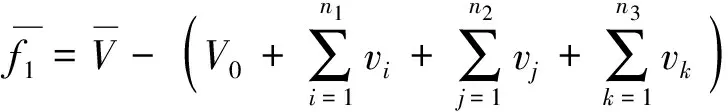
(3)

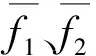
引入向量表示：

(4)

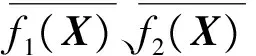
采用逐次線性化的方法得到方程組：

F′(Xk)ΔXk+F(Xk)=0；k=0，1，2，3，…

(5)

式中：Xk為經過k次迭代計算之后的結果；ΔXk為設定的計算精度，是迭代計算的停止條件；F′(Xk) 為F(X)在Xk處的Jacobi矩陣．根據船舶靜力學原理，有

(6)

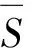
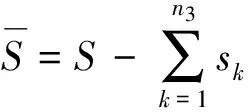
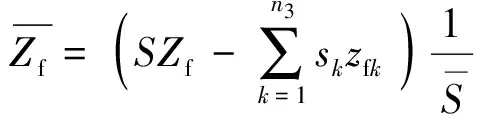
(7)

式中：S為破艙之后的水線面面積；s為進水艙室中的自由液面面積；Iyf為破艙之后的水線面對浮心的縱向慣性矩；iyf為進水艙室中自由液面對y軸的慣性矩．

2.3 程序設計

本文基于VS2013平臺，使用C++語言編寫破艙穩性的計算程序，具體的流程如圖2所示．先將船體的三維設計數據進行等距偏移得到船殼外表面三維設計數據，基于船殼外表面三維設計數據和艙室三維設計數據，確定船舶傾斜后的橫傾角，通過自由浮態計算簡化方法[14]得到船舶破損后的浮態參數，利用這些浮態數據求得船舶破損穩性復原力臂．

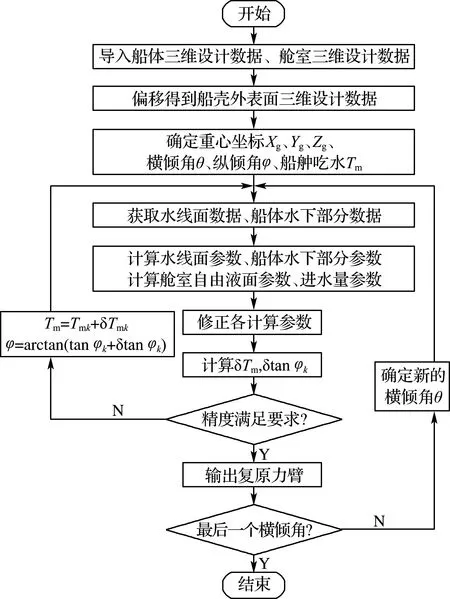
圖2 破艙穩性計算流程圖

3 算 例

本文基于散貨船“RUI AN CHENG”的三維設計數據，分別求取了該船在3種不同載況下1號貨艙破損、5號貨艙破損以及1號貨艙和5號貨艙同時破損時船舶的復原力臂曲線，貨艙的分布情況如圖3所示，從船艏到船艉方向分別為1號貨艙到5號貨艙．

圖3 散貨船“RUI AN CHENG”貨艙示意圖

3種載況分別為輕質貨滿載出港、重質貨均勻裝載出港、重質貨隔艙裝載出港，如圖4所示．

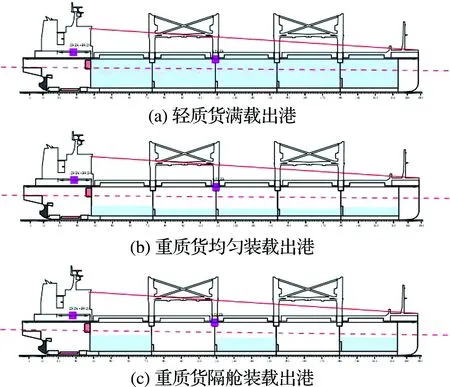
圖4 3種典型載況

表1為3種載況對應的浮態參數．

本文以這3種典型載況下的浮態為初始條件進行迭代，計算出橫傾角為0°～60°的復原力臂，然后將得到的復原力臂繪制成曲線與NAPA計算值進行比較．NAPA軟件是由芬蘭NAPA公司開發的國際著名的船舶CAD軟件，目前大約有32個國家的320多家單位使用NAPA作為船

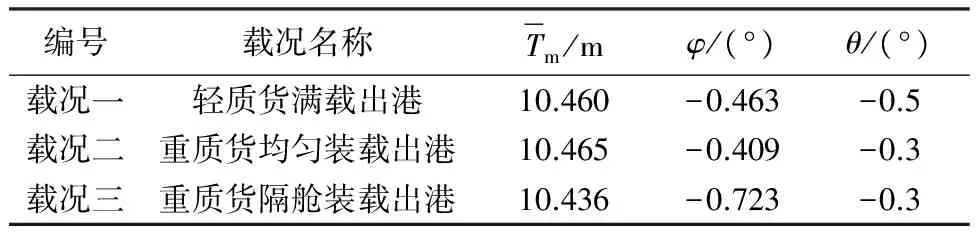
表1 典型載況

舶方案設計和技術設計的主要工具[15]．德國勞氏船級社和英國勞氏船級社等均將NAPA配載儀的計算結果作為標準值，根據與送檢配載儀計算結果的比對判斷送檢配載儀是否達到認可標準．

3.1 載況一

在輕質貨滿載出港的載況下，利用最小功法和靜平衡法分別在1號貨艙破損、5號貨艙破損以及1號貨艙和5號貨艙同時破損的情況下，求出橫傾角為0°～60°時的復原力臂，并與NAPA計算值進行對比，如圖5所示．

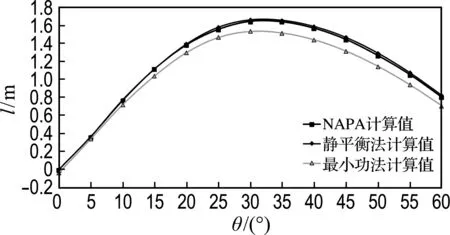
(a) 1號貨艙破損

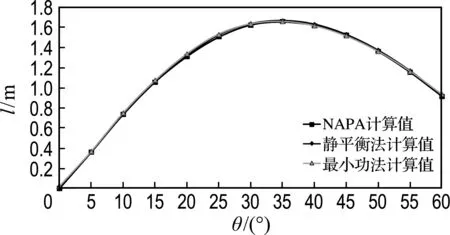
(b) 5號貨艙破損

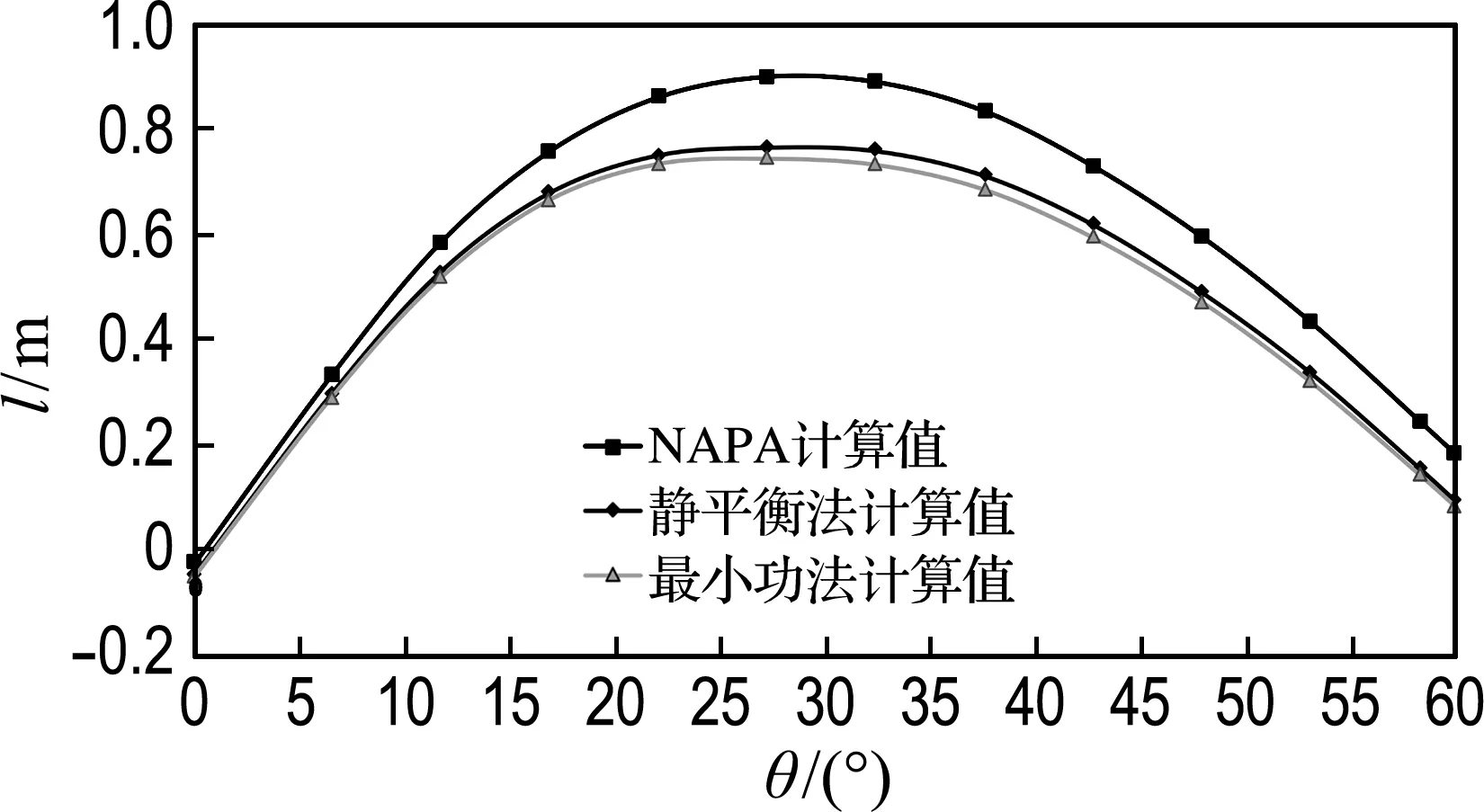
(c) 1號貨艙和5號貨艙同時破損

圖5 載況一的復原力臂對比曲線

Fig.5 GZ curves comparison under the first loading condition

3.2 載況二

在重質貨均勻裝載出港的載況下，利用最小功法和靜平衡法分別在1號貨艙破損、5號貨艙破損以及1號貨艙和5號貨艙同時破損的情況下，求出橫傾角為0°～60°時的復原力臂，并與NAPA計算值進行對比，如圖6所示．

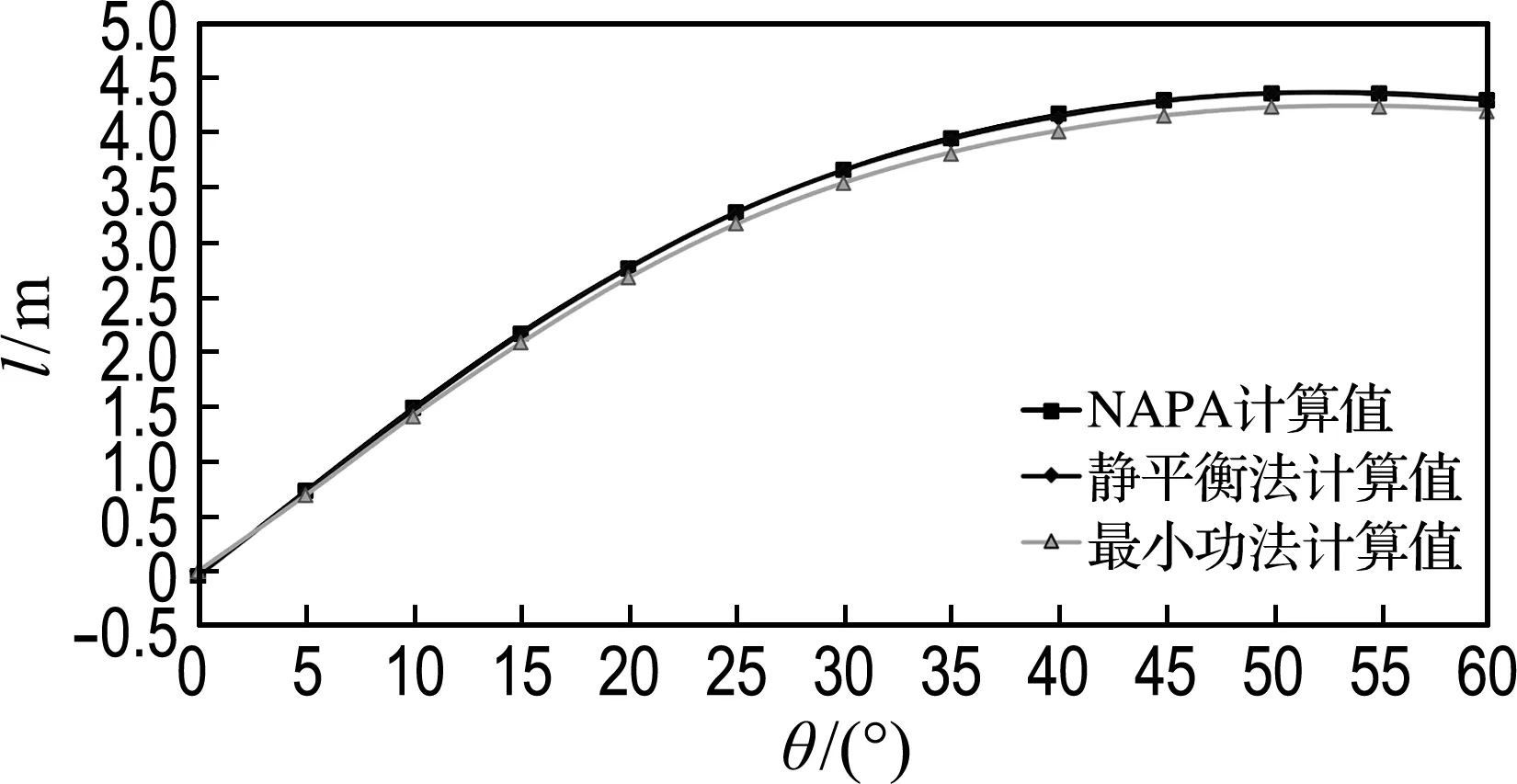
(a) 1號貨艙破損

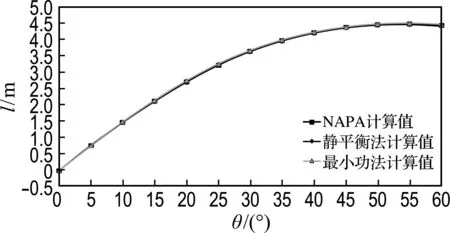
(b) 5號貨艙破損

(c) 1號貨艙和5號貨艙同時破損

圖6 載況二的復原力臂對比曲線

Fig.6 GZ curves comparison under the second loading condition

3.3 載況三

在重質貨隔艙裝載出港的載況下，利用最小功法和靜平衡法分別在1號貨艙破損、5號貨艙破損以及1號貨艙和5號貨艙同時破損的情況下，求出橫傾角為0°～60°時的復原力臂，并與NAPA計算值進行對比，如圖7所示．

3.4 誤差分析

將NAPA計算結果近似看作準確值，表2、3分別為使用最小功法和靜平衡法計算產生的誤差．

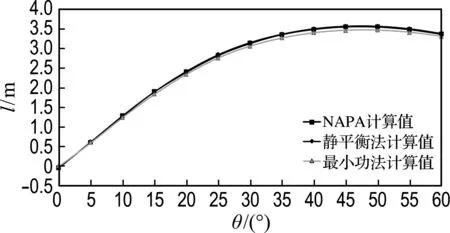
(a) 1號貨艙破損

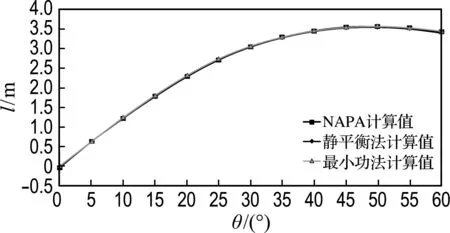
(b) 5號貨艙破損

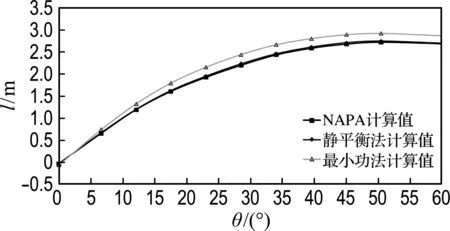
(c) 1號貨艙和5號貨艙同時破損

圖7 載況三的復原力臂對比曲線

Fig.7 GZ curves comparison under the third loading condition

德國勞氏船級社[16]和英國勞氏船級社[17]對基于三維設計數據的散貨船配載儀中的穩性計算誤差要求最大不超過5 cm或5%．

利用最小功法進行破艙穩性的計算，117次計算中最大絕對誤差為0.318 m(相對誤差為10.82%)；每次計算的平均絕對誤差為0.091 m(相對誤差為1.86%)．實驗證明本方法不符合船級社的精度要求，不適用于散貨船配載儀中破艙穩性計算模塊的實現．

利用靜平衡法進行破艙穩性的計算，117次計算中最大絕對誤差為0.031 m(相對誤差為1.06%)；每次計算的平均絕對誤差為0.013 m(相對誤差為0.42%)，符合船級社的精度要求．而且在不同載況下，設置不同的橫傾角，計算中迭代次數為3、4、5的概率為82.91%，迭代次數為6、7、8的情況只出現在橫傾角超過50°時，滿足計算的實時性要求，如圖8所示．

最小功法不保證船舶橫傾之后縱向外力和外力矩的平衡，所以計算結果和靜平衡法有所差別．由誤差分析可知，NAPA的破艙穩性計算模塊使用的不是最小功法．

由實驗結果可知，靜平衡法計算船舶的破艙穩性與NAPA的計算結果較為接近．基于靜平衡法，大連海事大學航海研究所成功完成了配載儀中的破艙穩性計算模塊，并與上海船舶研究設計院聯合開發了smart load型配載儀，該型配載儀的主界面如圖9所示．目前，該配載儀已經通過CCS的認證并已順利裝船．

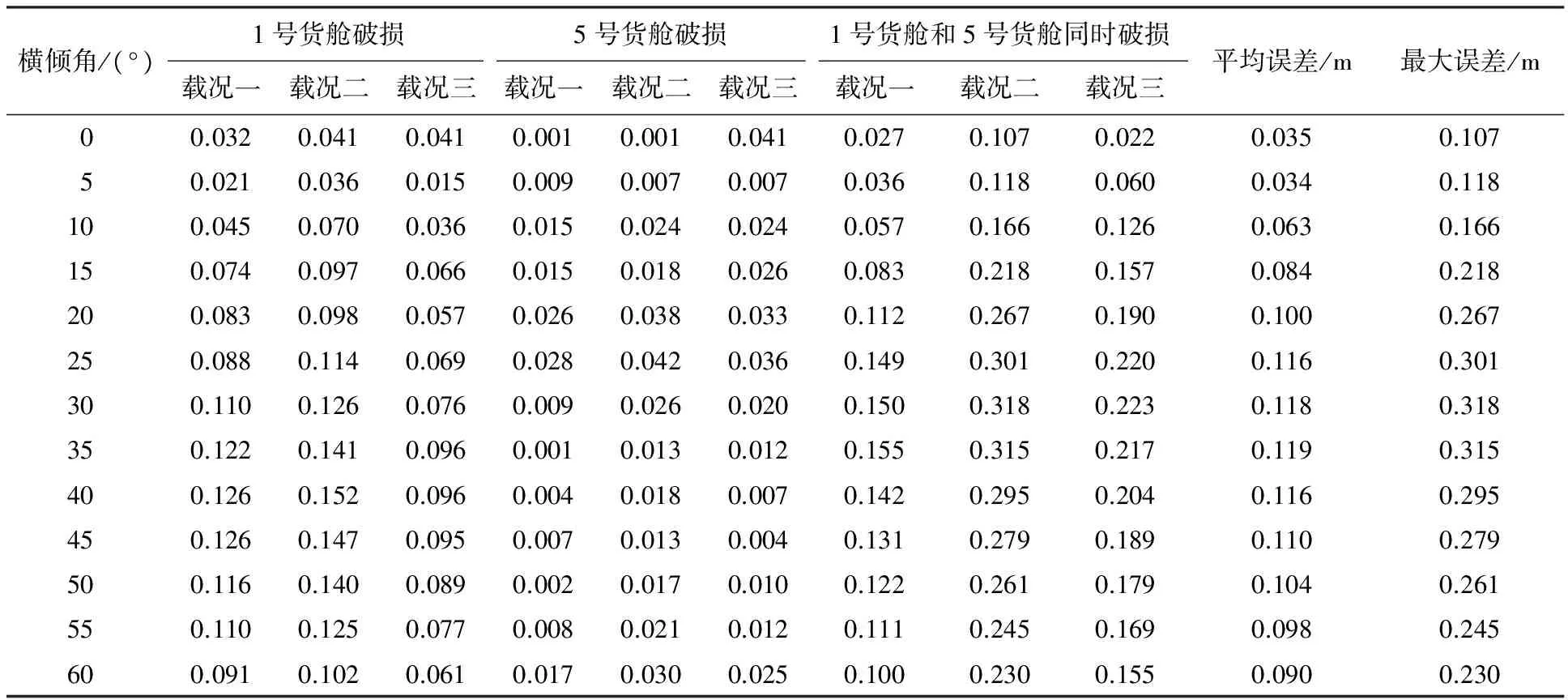
表2 最小功法計算結果絕對誤差

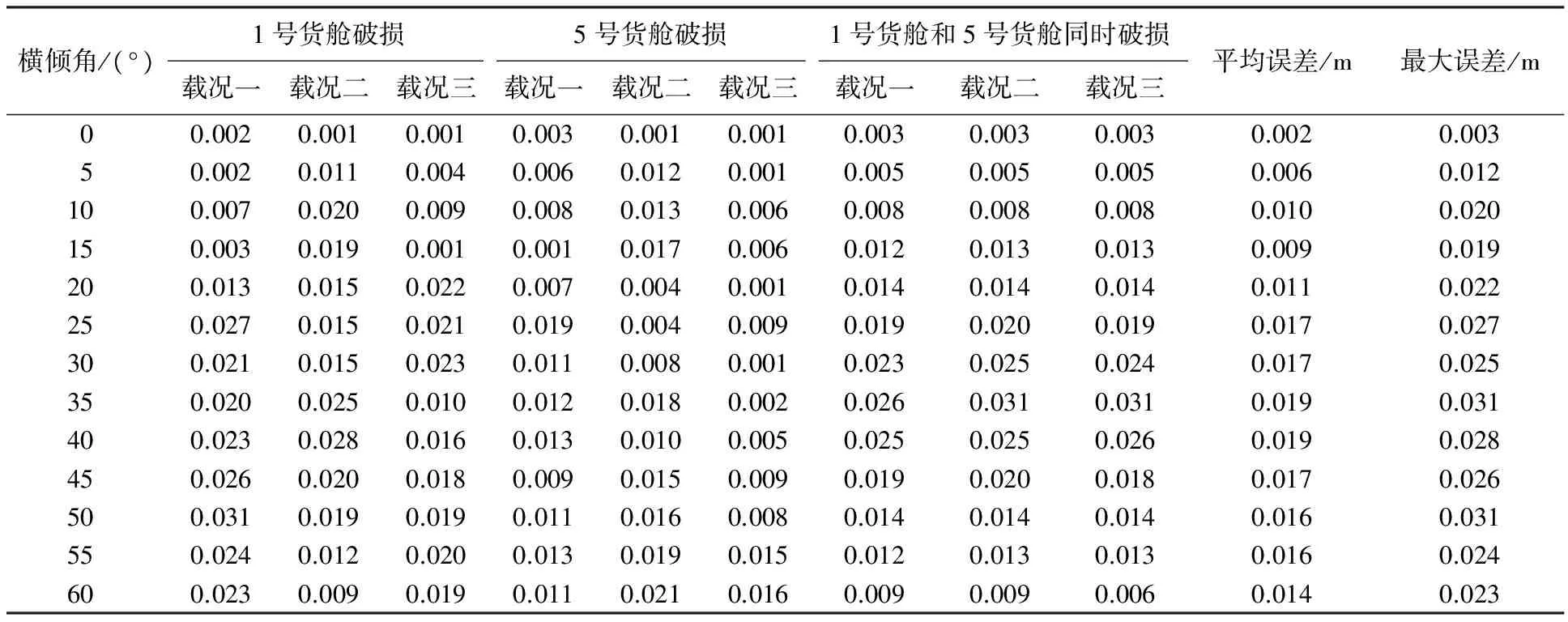
表3 靜平衡法計算結果絕對誤差

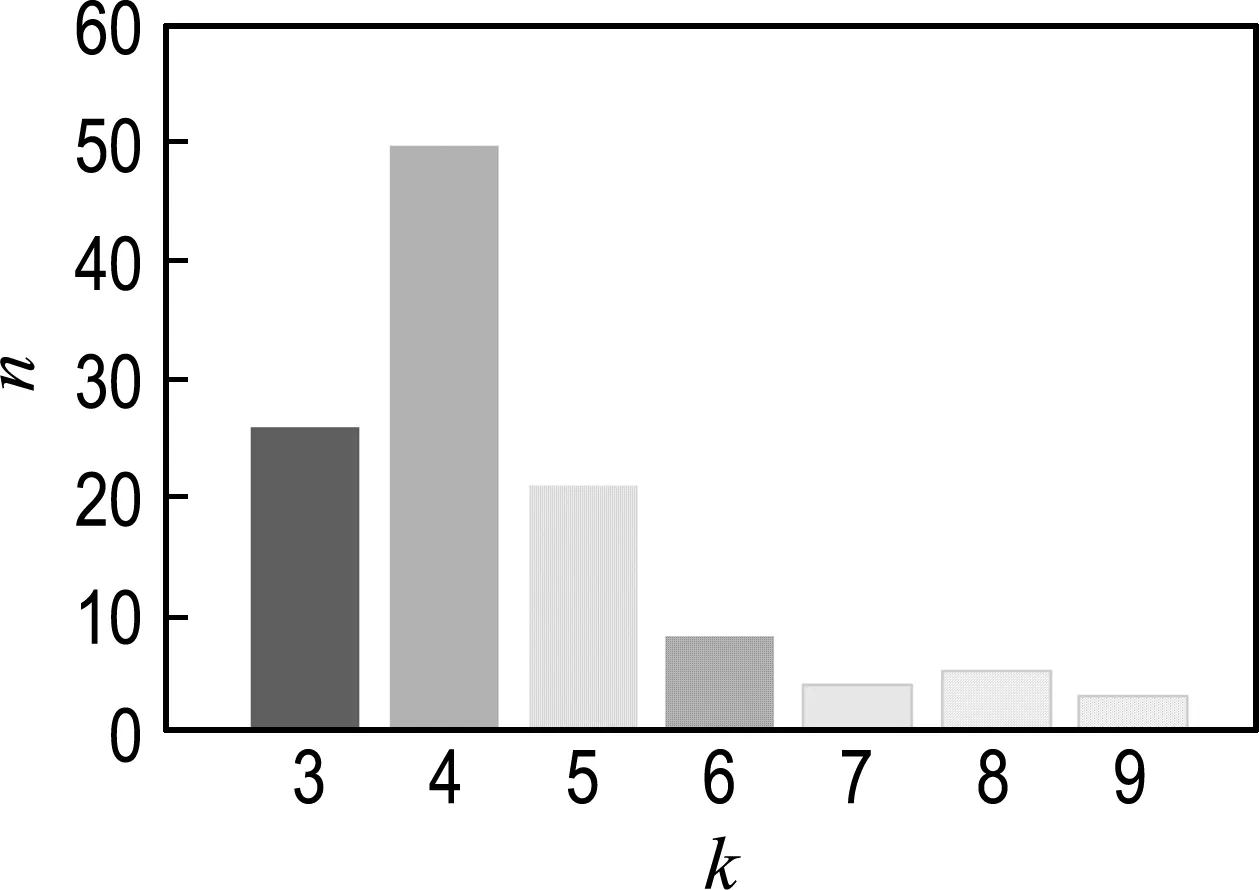
圖8 破艙穩性計算迭代次數分布

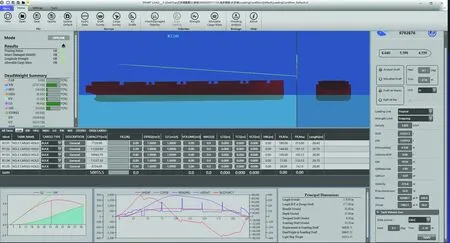
圖9 散貨船配載儀主界面

4 結 語

本文通過對船殼型表面數據進行船舶外板厚度的等距偏移，得到船體外板的設計數據，然后以適當的間隔沿船長方向進行切片得到船殼外表面的三維設計數據．以船舶外表面三維設計數據和艙室三維設計數據為基礎進行破艙穩性的計算，得到破艙穩性曲線．通過對最小功法和靜平衡法下的破艙穩性計算進行實現，發現運用不同的計算方法，得到的計算結果差異較大．使用靜平衡下的自由縱傾法得到的計算結果與NAPA的計算結果較為接近．利用船舶的三維船殼模型計算破艙穩性具有較高的精度．本文介紹的方法不僅適用于散貨船配載儀中破艙穩性計算模塊的實現，對液貨船、集裝箱船等船型配載儀的開發也具有一定的參考價值．

[1] 盛振邦,楊尚榮,陳雪深. 船舶靜力學[M]. 上海:上海交通大學出版社, 1984.

SHENG Zhenbang, YANG Shangrong, CHEN Xueshen.ShipStatics[M]. Shanghai:Shanghai Jiao Tong University Press, 1984. (in Chinese)

[2] 姜 玲. 船舶穩性三維計算方法研究及軟件開發[D]. 大連:大連海事大學, 2015.

JIANG Ling. Ship stability dimensional calculation method research and software development [D]. Dalian: Dalian Maritime University, 2015. (in Chinese)

[3] 周瑞平,郭汝緋. 基于VB.NET的船舶穩性計算軟件的設計和實現[J]. 造船技術, 2008,4(8):41-44.

ZHOU Ruiping, GUO Rufei. The design and realization of ship stability software based on VB.NET [J].MarineTechnology, 2008,4(8):41-44. (in Chinese)

[4] 段興鋒. 基于型值表的船舶裝載儀的研究[D]. 大連:大連海事大學, 2008.

DUAN Xingfeng. Research of ship stowage system based on table of offsets [D]. Dalian: Dalian Maritime University, 2008. (in Chinese)

[5] 蔡曉梅. 應用三維船體曲面模型進行破艙穩性計算[J]. 江蘇船舶, 2005,22(5):1-3.

CAI Xiaomei. Application of three-dimensional hull surface model in damaged stability calculation [J].JiangsuShip, 2005,22(5):1-3. (in Chinese)

[6] 林 焰,李鐵驪,紀卓尚. 破損船舶自由浮態計算[J]. 大連理工大學學報, 2001,41(1):85-89.

LIN Yan, LI Tieli, JI Zhuoshang. Ship damage floating calculation [J].JournalofDalianUniversityofTechnology, 2001,41(1):85-89. (in Chinese)

[7] 肖維維,李俊華,何 剛,等. 船舶破艙穩性計算方法研究[J]. 中國水運, 2006,4(11):12-14.

XIAO Weiwei, LI Junhua, HE Gang,etal. Study of ship damage stability calculation [J].ChinaWaterTransport, 2006,4(11):12-14. (in Chinese)

[8] 王彩蓮. 淺談船舶應用軟件NAPA[J]. 船舶, 2004(3):58-60.

WANG Cailian. On the ship design software NAPA [J].Ship&Boat, 2004(3):58-60. (in Chinese)

[9] 蔣毅文. Maxsurf及相關設計程序在船舶設計中的應用[J]. 船海工程, 2005(4):39-41.

JIANG Yiwen. Application of Maxsurf and corresponding software in ship design [J].Ship&OceanEngineering, 2005(4):39-41. (in Chinese)

[10] 劉春雷,尹 勇,孫霄峰,等. 基于STL模型的船舶幾何特性計算[J]. 系統仿真學報, 2015,27(10):2264-2271.

LIU Chunlei, YIN Yong, SUN Xiaofeng,etal. Calculation of vessel′s geometric properties based on STL model [J].JournalofSystemSimulation, 2015,27(10):2264-2271. (in Chinese)

[11] 孫承猛,劉寅東. 一種船舶最小穩性和自由浮態計算的改進算法[J]. 中國造船, 2007,48(3):1-4.

SUN Chengmeng, LIU Yindong. An improved algorithm for calculating ship′s minimum stability and free floatation [J].ShipbuildingofChina, 2007,48(3):1-4. (in Chinese)

[12] 趙曉非,蔡偉科. 船舶穩性計算優化方法研究[J]. 中國造船, 1987,40(2):86-92.

ZHAO Xiaofei, CAI Weike. An optimization method for the calculation of ship stability curves [J].ShipbuildingofChina, 1987,40(2):86-92. (in Chinese)

[13] 趙曉非,林 焰. 關于解船舶浮態問題的矩陣方法[J]. 中國造船, 1985(3):55-64.

ZHAO Xiaofei, LIN Yan. Matrix methods for solving ship floating state problem [J].ShipbuildingofChina, 1985(3):55-64. (in Chinese)

[14] 劉春雷,尹 勇,孫霄峰,等. 散貨船自由浮態計算簡化方法[J]. 大連理工大學學報, 2017,57(1):55-60.

LIU Chunlei, YIN Yong, SUN Xiaofeng,etal. Simplified method of bulk carrier′s free floatation calculation [J].JournalofDalianUniversityofTechnology, 2017,57(1):55-60. (in Chinese)

[15] 劉春雷. 散貨船智能化配載儀的研究與實現[D]. 大連:大連海事大學, 2013.

LIU Chunlei. Research and implementation of intelligent bulk carrier stowage system [D]. Dalian:Dalian Maritime University, 2013. (in Chinese)

[16] Germanischer Lloyd SE. Rules for Classification and Construction [Z]. Hamburg:Germanischer Lloyd SE, 2013.

[17] Lloyd′s Register. Approval of Longitudinal Strength and Stability Calculation Programs [Z]. London: Lloyd′s Register, 2011.