摻雜三角形硼氮片的鋸齒型石墨烯納米帶的磁電子學性質?

張華林 孫琳 韓佳凝

(長沙理工大學物理與電子科學學院,長沙 410114)

(2017年7月26日收到;2017年9月17日收到修改稿)

1 引 言

自從2004年Novoselov等[1]成功制備單層石墨烯以來,石墨烯以其獨特的性質引起了物理、化學、材料等學科研究人員的廣泛關注.石墨烯納米帶是一種準一維碳納米材料,根據邊界結構不同,石墨烯納米帶分為鋸齒型石墨烯納米帶(ZGNR)和扶手椅型石墨烯納米帶(AGNR).不考慮自旋時,ZGNR為金屬;考慮自旋時,其鐵磁(FM)態為金屬,而反鐵磁(AFM)態為半導體[2?5].對于石墨烯納米帶電子特性調制的研究已有很多報道,主要分為摻雜、吸附[6,7]、邊緣修飾[8?10]和引入缺陷[11?13]等調控手段,其中摻雜對石墨烯的結構和電子性能的影響是一項非常值得關注的工作.在有關摻雜的研究中,有很多關于硼(B)和氮(N)原子摻雜的研究工作,而對于B和N摻雜,又設計有不同形式.有的在石墨烯納米帶中單獨摻雜B或N原子[14,15],有的在一個較大超原胞中只摻雜一對B和N原子[16,17],有的成排摻雜B和N原子對[5,15],還有的將BN片摻雜到石墨烯中.Xu等[18]研究了BN片摻雜對石墨烯超晶格的電子與磁性的影響,發現不管BN片的形狀是六邊形還是三角形,石墨烯超晶格的帶隙隨著BN片的增大而增加.Manna和Pati[19]研究了嵌入BN片的二維石墨烯片的電子結構和磁性特征,研究表明嵌入BN的形狀(含六邊形和三角形)和大小對二維石墨烯片的電子結構有顯著影響.Menezes和Capaz[20]研究了三角形h-BN分子團嵌入石墨烯超晶胞的電子結構和磁性.He等[21]提出了一種由鋸齒型氮化硼納米帶和ZGNR構造的混合結構,并計算其能帶結構及電子輸運性質,結果表明混合結構的帶隙可以調整,通過改變ZGNR的寬度可以實現從絕緣體到金屬的轉變,且不同自旋極化電流表現出不同的行為.Seol和Guo[22]研究了由BN納米帶約束的AGNRs的電子性質.

基于最近實驗已實現在二維石墨烯中摻雜BN片的混合納米結構[23],本文采用基于密度泛函理論(DFT)的第一性原理,探討三角形BN片摻雜的ZGNR,在無磁(NM)態、FM態和AFM態三種情況下的磁電子學特性.這些研究結果對于發展基于石墨烯的納米電子器件有重要意義.

2 計算模型與方法

BN片摻雜的ZGNR的幾何結構如圖1所示.圖中藍色虛線方框表示最小周期性重復單元,即計算選取的超原胞;白色、灰色、粉紅色和藍色原子分別為H,C,B和N原子;n表示完整ZGNR的帶寬,即沿寬度方向的鋸齒型碳原子鏈的排數.本文計算的模型選取帶寬n=7的ZGNR作為代表.超原胞中的紅色虛線三角形表示摻雜的位置,用Pi編號,其中i=1,2,3,4,5.圖1中給出了P3位置摻雜的模型,P3位置的三角形內的所有C原子被BN原子取代,共6個B原子和7個N原子.為了消除懸掛鍵,所有ZGNR邊緣用H原子飽和.

圖1 (網刊彩色)三角形BN片摻雜的ZGNR的計算模型Fig.1.(color online)The geometric structure of ZGNR doped with triangular BN segment.

采用基于DFT的第一性原理的ATK(Atomistix ToolKit)軟件包計算幾何結構優化和電磁性質[24?26],目前它已被廣泛用于納米結構的研究中.模型結構在非磁性下進行優化.結構優化收斂的標準是作用在每個原子上的力小于0.02 eV/?.為了求解Kohn-Sham方程,交換關聯勢采用廣義梯度近似中的Perdew-Burke-Ernzerhof近似,贗勢采用模守恒贗勢,基函數組選用DZP(Doubleζ+Polarized).在簡約布里淵區的k點抽樣采用1×1×50.能量截取半徑(mesh cut-off)采用150 Ry.X和Y方向超原胞的真空層設置為15 ?.

3 計算結果與討論

3.1 NM態

ZGNR在NM態的能帶結構和態密度(DOS)如圖2所示,圖2(a)–(f)分別表示未摻雜ZGNR和P1–P5位置摻雜的ZGNR(下同).圖2中Z表示未摻雜ZGNR,Pi(i=1,2,3,4,5)表示摻雜的位置,BS表示能帶結構,DOS表示態密度(下同),PDOS表示投影態密度,在此為投影到C原子的投影態密度.圖2中縱軸為能量(E/eV),過縱軸零點的虛線表示費米能級(下同).各模型的超原胞未取代摻雜時共有42個碳原子,各摻雜模型被BN原子取代的C原子數為13個.定義摻雜濃度為被BN分子取代的C原子數與未取代摻雜時的C原子總數的比值,則各模型的摻雜濃度都為31.0%.由圖2可見,摻雜后ZGNR的能帶結構發生了一定的變形和移動.不論是否摻雜,ZGNR都有子能帶穿越費米能級,且在緊靠費米能級的位置,穿越費米能級的子能帶都有一段非常平緩.DOS與其相應的能帶結構有很好的對應性,能帶平緩處DOS出現峰值,能帶陡峭處DOS較小,而沒有能帶分布處DOS為零.不論是否摻雜,ZGNR的DOS在費米能級處都出現一個較大的峰值.由此可見,不論是否摻雜,ZGNR都無帶隙,都為金屬.不論是否摻雜,ZGNR的PDOS圖都與相應的DOS圖都有很好的對應性,只是峰值大小略有差異,可見在能量為?1–1 eV范圍內,ZGNR的DOS主要由C原子貢獻.

為了更清楚地分析哪些原子對穿越費米能級的子能帶起作用,圖3繪出了各模型該子能帶的電荷密度圖,等值面取0.05|e|??3.由圖3可見,ZGNR穿越費米能級的子能帶主要由第1排和第7排C鏈中靠近邊緣的C原子起作用,其次為第2排和第6排C鏈中靠近邊緣的C原子.BN摻雜對摻雜區域的電荷密度具有明顯的抑制作用.由此可見,由于摻雜位置的不同,電荷密度被抑制的區域不同,導致對各摻雜ZGNR的穿越費米能級的子能帶起作用的原子不同,從而導致該子能帶略有不同程度的移動和變形.

圖2 NM態的能帶結構和DOSFig.2.The band structure and density of states in the nonmagnetic state.

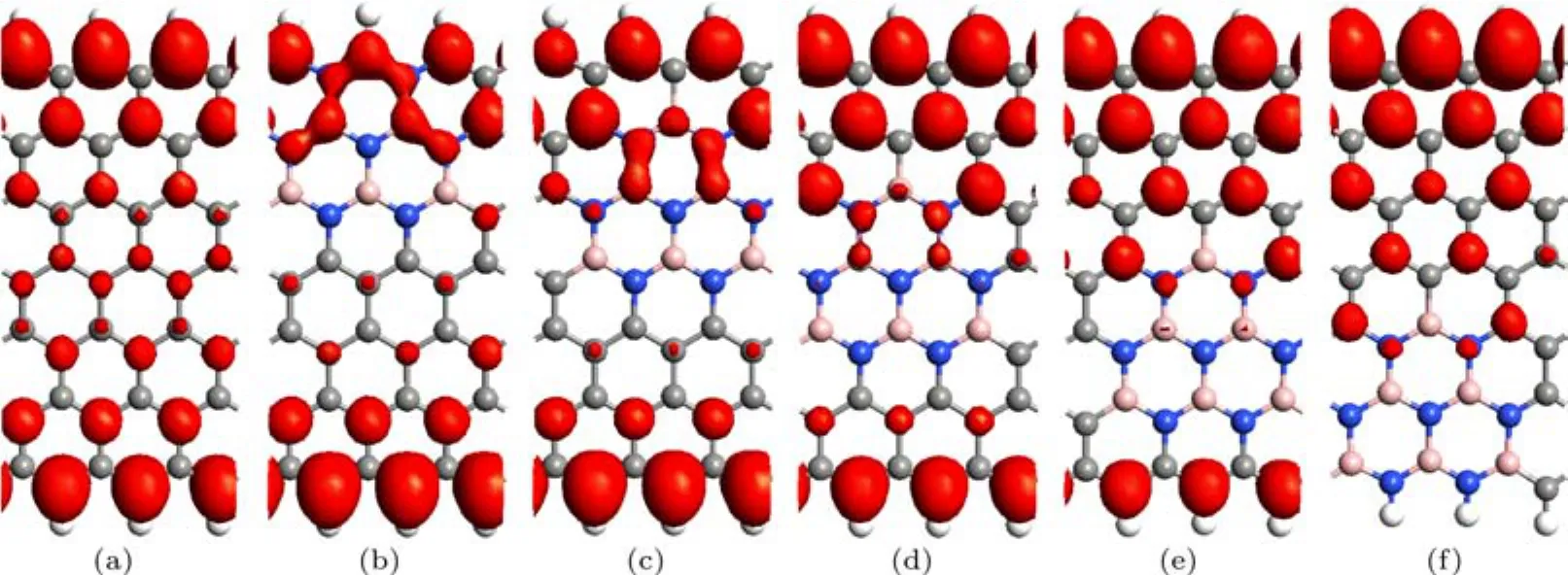
圖3 (網刊彩色)部分子能帶的電荷密度 (a)Z;(b)P1;(c)P2;(d)P3;(e)P4;(f)P5Fig.3.(color online)The charge density of partial subband:(a)Z;(b)P1;(c)P2;(d)P3;(e)P4;(f)P5.

3.2 FM態

圖4 (網刊彩色)自旋極化電荷密度等值面圖 (a)Z;(b)P1;(c)P2;(d)P3;(e)P4;(f)P5Fig.4.(color online)The isosurface plots of spin polarization charge density in the ferromagnetic state:(a)Z;(b)P1;(c)P2;(d)P3;(e)P4;(f)P5.

ZGNR在FM態的自旋極化電荷密度等值面如圖4所示.圖4中紅色和藍色分別代表α和β自旋,等值面取0.01|e|?3(下同).自旋極化電荷密度Δρ=ρα?ρβ,其中ρα和ρβ分別表示α和β自旋的電荷密度.由圖4可見,未摻雜的ZGNR和P2–P4位置摻雜的ZGNR的自旋極化電荷密度的共同特點是,上下兩邊緣的自旋方向相同,其磁性狀態都表現為FM性.各摻雜的ZGNR中BN摻雜區域的自旋極化電荷密度均受到明顯的抑制.這一點也可以從各模型的超原胞的總磁矩反映出來,未摻雜的ZGNR和P1–P5位置摻雜的ZGNR超原胞的總磁矩分別為1.51μB,0.60μB,1.00μB,1.01μB,1.00μB,0.95μB,μB為玻爾磁子.可見各摻雜的ZGNR的總磁矩明顯小于未摻雜的ZGNR的總磁矩.對于P1和P5位置摻雜的ZGNR,由于都有BN原子位于納米帶的邊緣,雜質所在邊緣的自旋極化電荷密度受到抑制,這種情況其磁性狀態也表現為FM性.由于B或N原子中的3個價電子與鄰近的原子成鍵,B原子已沒有剩余的未成鍵的價電子去貢獻磁性,而N原子雖然還有2個剩余的未成鍵的價電子,但其自旋方向相反,無凈磁矩,故BN摻雜對摻雜區域自旋極化電荷密度有明顯的抑制作用[5].

ZGNR在FM態的能帶結構和DOS如圖5所示,圖中藍色實線和紅色實線分別表示α和β自旋(下同).由圖5可見,不論是否摻雜,ZGNR在費米能級附近的能帶都發生了分裂,且α自旋的能帶向下移動,β自旋的能帶向上移動.結合圖4和各模型的總磁矩為正,可以知道α自旋為多子態,而β自旋為少子態.正是因為α自旋是多子態,才導致費米能級附近α自旋的能帶向下移動,以提供更多態讓電子填充,而β自旋是少子態,導致β自旋的能帶向上移動,減少可供電子填充的態.未摻雜ZGNR和P1位置摻雜的ZGNR的α和β自旋都有能帶穿越費米能級,且在費米能級處的DOS都不為零,故都為自旋金屬.P2–P4位置摻雜的ZGNR的α自旋都沒有能帶穿越費米能級,且在費米能級處的DOS都為零,而β自旋都有能帶穿越費米能級,且在費米能級處的DOS都不為零,故都為自旋半金屬.P2–P4位置摻雜的ZGNR的α自旋都具有直接帶隙,導帶底和價帶頂都位于Γ點,帶隙大小略有差異,分別為0.284,0.279,0.347 eV.自旋半金屬對實現自旋過濾有重要意義.P5位置摻雜的ZGNR的α和β自旋都沒有能帶穿越費米能級,在費米能級處的DOS都為零,故為自旋半導體,且為雙極化自旋半導體,其上旋和下旋帶隙分別為0.341 eV和0.118 eV.雙極化自旋半導體對于在改變柵極偏壓正負時,實現雙自旋過濾有重要意義.可見在ZGNR中摻雜三角形BN片,當處于FM態時,隨著摻雜位置的改變,可以實現自旋金屬-自旋半金屬-自旋半導體的變化過程,且非常有意思的是只要摻雜區域不在邊緣,摻雜的ZGNR就為自旋半金屬.

3.3 AFM態

ZGNR在AFM態的自旋極化電荷密度等值面如圖6所示.由圖6可見,未摻雜的ZGNR和P2–P4位置摻雜的ZGNR的自旋極化電荷密度的共同特點是,上下兩邊緣的自旋方向相反,其磁性狀態都表現為AFM性.摻雜的ZGNR中BN摻雜區域的自旋極化電荷密度均受到明顯的抑制.P1和P5位置摻雜的ZGNR,由于摻雜區域都有BN原子位于納米帶的邊緣,雜質所在邊緣的自旋極化電荷密度受到抑制,這種情況其磁性狀態依然表現為FM性,即P1和P5位置摻雜的ZGNR沒有AFM態.

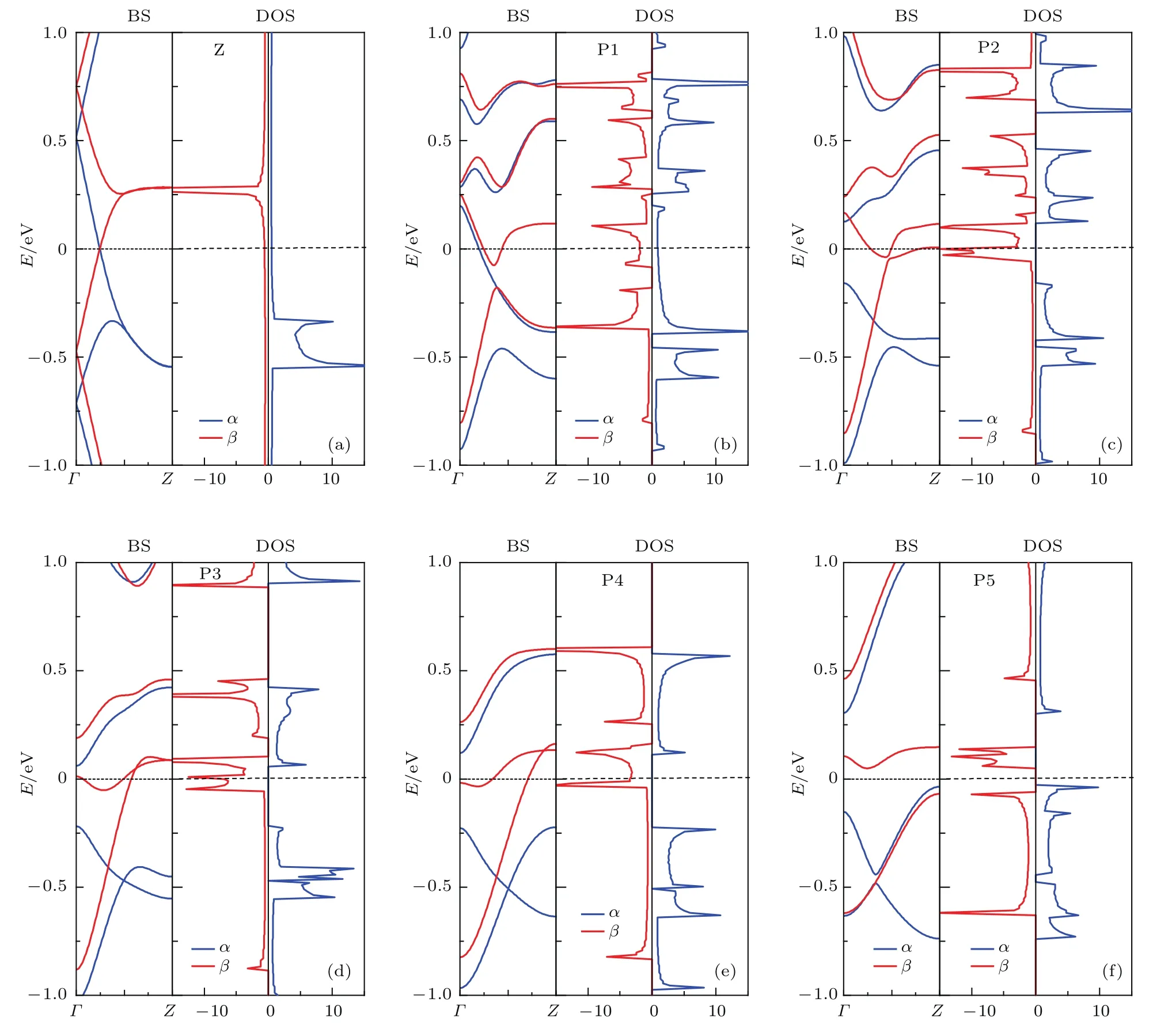
圖5 (網刊彩色)FM態的能帶結構和DOSFig.5.(color online)The band structure and density of states in the ferromagnetic state.

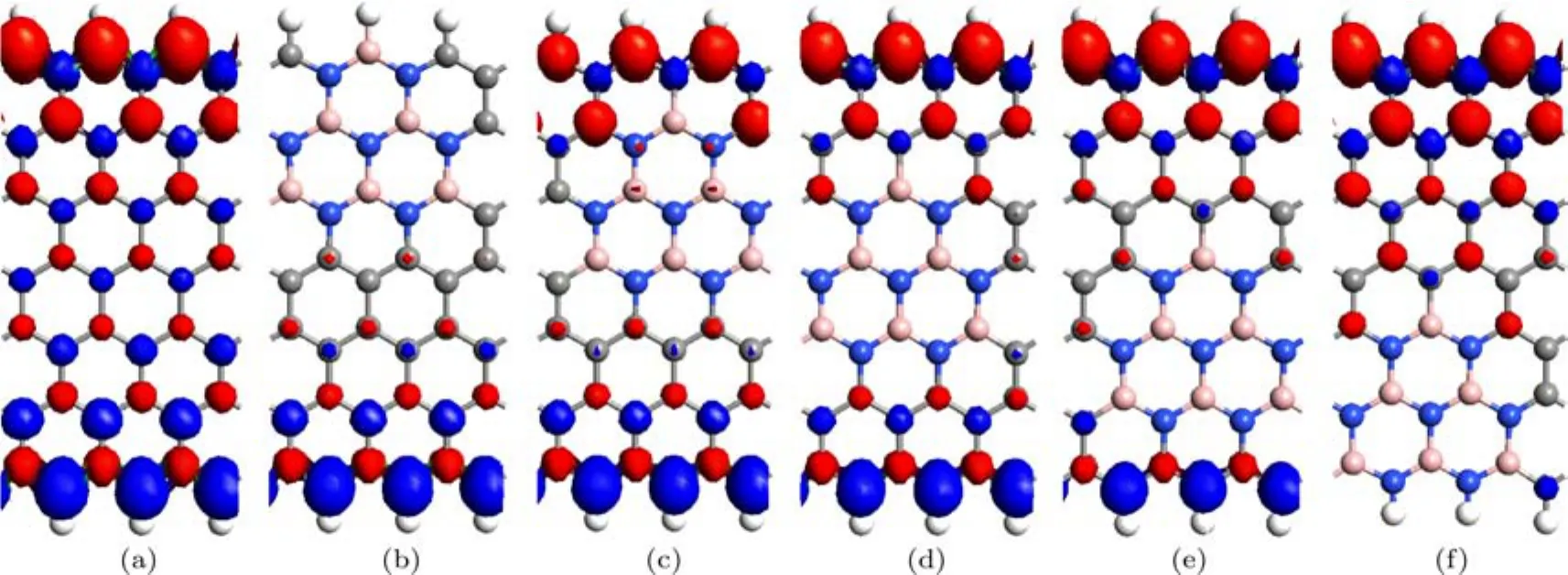
圖6 (網刊彩色)自旋極化電荷密度等值面圖 (a)Z;(b)P1;(c)P2;(d)P3;(e)P4;(f)P5Fig.6.(color online)The isosurface plots of spin polarization charge density in the antiferromagnetic state:(a)Z;(b)P1;(c)P2;(d)P3;(e)P4;(f)P5.

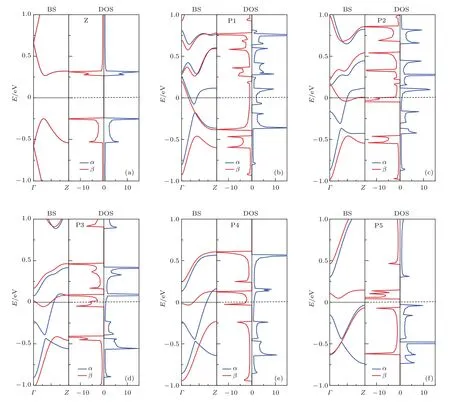
圖7 (網刊彩色)AFM態的能帶結構和DOSFig.7.(color online)The band structure and density of states in the antiferromagnetic state.

ZGNR在AFM態的能帶結構和DOS如圖7所示.由圖7可見,未摻雜ZGNR在費米能級附近的能帶是簡并的,沒有能帶穿越費米能級,且在費米能級處的DOS為零,故為半導體,其α和β自旋的帶隙大小都為0.518 eV.未摻雜ZGNR的α和β自旋極化電荷密度關于對稱軸成對稱分布,總磁矩為零,α和β自旋電子是均衡的,故導致其能帶簡并.但摻雜的ZGNR在費米能級附近的能帶都發生了分裂,這是因為BN摻雜區域的自旋極化電荷密度受到抑制,導致α和β自旋電子不再均衡.P2–P4位置摻雜的ZGNR的α和β自旋都有能帶穿越費米能級,且在費米能級處的DOS都不為零,故都為自旋金屬.結合圖5和圖7可見,P5位置摻雜的ZGNR在FM態和AFM態的能帶結構是相同的,因為兩種自旋極化電荷密度是相同的,總磁矩都是0.95μB,都是α自旋為多子態;而P1位置摻雜的ZGNR在FM態和AFM態的能帶結構形式相同,只是α和β自旋正好交換了,這是因為在FM態時α自旋為多子態,AFM態的總磁矩為?0.60μB,其β自旋為多子態,由對稱性可知,其AFM態實質上還是FM態.這進一步說明了P1和P5位置摻雜的ZGNR沒有AFM態.

3.4 結構穩定性分析

為了研究取代摻雜結構的穩定性,分別取各位置摻雜的ZGNR的超原胞,計算結合能和不同磁性態的總能差.各位置摻雜的ZGNR的總能差(ΔE/meV)和結合能如圖8所示.定義FM態與AFM態的總能差ΔE1=EFM?EAFM,NM態與AFM態的總能差ΔE2=ENM?EAFM,EFM,EAFM和ENM分別為各超原胞在FM態、AFM態和NM態的總能.定義結合能

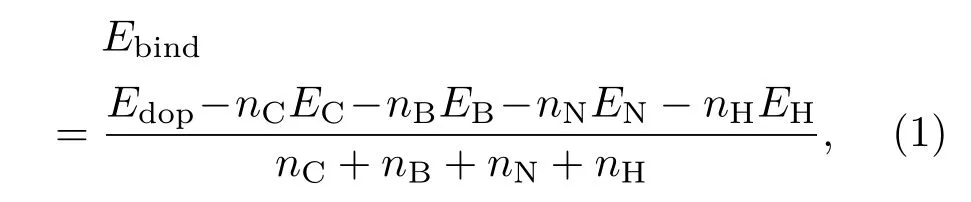
式中,Edop為摻雜ZGNR的超原胞的總能量;EC,EB,EN,EH分別為單個C,B,N,H原子的能量;nC,nB,nN,nH分別為超原胞內C,B,N,H原子的數量[27].由圖8可見,對于各位置摻雜的ZGNR都有ΔE2＞0,即ENM＞EAFM;對于P2–P4位置摻雜的ZGNR有ΔE1＞0,即EFM＞EAFM;而對于P1和P5位置摻雜的ZGNR有ΔE1=0,即EFM=EAFM,表明P2–P4位置摻雜的ZGNR的基態是AFM態,P1和P5位置摻雜的ZGNR沒有AFM態,其基態為FM態.發現P1–P5位置摻雜的ZGNR的結合能都為負值,且結合能的大小都與參考文獻[27]中的數值(?8.13 eV)非常接近,說明摻雜的ZGNR的結構是穩定的.隨著摻雜位置由P1向P5移動,結合能逐漸減小,P5位置摻雜的ZGNR的結合能最小,說明在P5位置摻雜的ZGNR的結構最穩定.

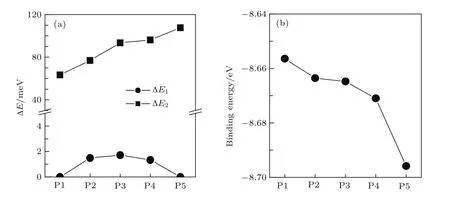
圖8 各位置摻雜的ZGNR的(a)總能差和(b)結合能Fig.8.(a)The total energy differences and(b)the binding energies for the ZGNRs doped with triangular BN segments at different positions.

3.5 尺度效應

為了研究在不同寬度ZGNR中相同位置摻雜相同大小的BN片的磁電子學特性,在此建立兩個與P2模型類似的模型,ZGNR的帶寬分別為n=6和8,即保持BN片的大小和位置不變,將n=7的ZGNR模型的下邊緣分別減少和增加一排碳鏈,這兩個模型分別用Z6和Z8表示.Z6和Z8模型的摻雜濃度分別為36.1%和27.1%,即隨著ZGNR帶寬的增大,摻雜濃度減小,計算參數同上.Z6和Z8模型在NM,FM和AFM態的能帶結構如圖9所示.由圖9可見,在NM態,Z6和Z8模型都有能帶穿越費米能級,都為金屬.結合圖2(c)可知,當處于NM態時,在P2位置摻雜相同大小的BN片,改變ZGNR的寬度,其屬性不變,都為金屬.在FM態,Z6和Z8模型的α自旋都沒有能帶穿越費米能級,而β自旋都有能帶穿越費米能級,故都為自旋半金屬.結合圖5(c)可知,當處于FM態時,在P2位置摻雜相同大小的BN片,改變ZGNR的寬度,其屬性不變,都為自旋半金屬.帶寬n=6,7,8的摻雜ZGNR的上旋能帶都有直接帶隙,其帶隙大小分別為0.373,0.284,0.234 eV,可見在所研究的帶寬范圍內,隨著ZGNR帶寬的增大,上旋帶隙逐漸減小.在AFM態,Z6和Z8模型的α自旋和β自旋都有能帶穿越費米能級,故都為自旋金屬.結合圖7(c)可知,當處于AFM態時,在P2位置摻雜相同大小BN片,改變ZGNR的寬度,其屬性不變,都為自旋金屬.可見在所研究的帶寬范圍內,保持BN摻雜區域的大小和位置不變,改變ZGNR的帶寬,三種磁性態下各自的屬性保持不變.

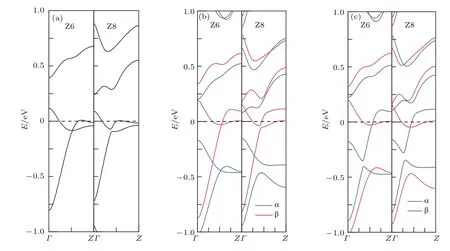
圖9 (網刊彩色)不同寬度摻雜ZGNR的能帶結構 (a)NM;(b)FM;(c)AFMFig.9.(color online)The band structures of doping ZGNRs with different widths:(a)NM;(b)FM;(c)AFM.

4 結 論

利用基于DFT的第一性原理研究了三角形BN片摻雜對ZGNR的磁電子學性質的影響.研究表明:當處于NM態時,各位置摻雜的ZGNR都為金屬.BN摻雜對ZGNR的自旋極化電荷密度具有明顯的抑制作用,導致考慮自旋時,不同位置摻雜的ZGNR呈現不同的屬性;當處于FM態時,隨著雜質在ZGNR中由P1位置向P5位置移動,依次可以實現自旋金屬-自旋半金屬-自旋半導體的變化過程,且只要摻雜區域不在ZGNR的邊緣,摻雜的ZGNR就為自旋半金屬;當處于AFM態時,P2–P4位置摻雜的ZGNR都為自旋金屬.P1和P5位置摻雜的ZGNR沒有AFM態.P2–P4位置摻雜的ZGNR的基態是AFM態,P1和P5位置摻雜的ZGNR的基態為FM態.P1–P5位置摻雜的ZGNR的結合能都為負值,且隨著摻雜位置由P1向P5移動,結合能逐漸減小,P5位置摻雜的ZGNR的結合能最小,說明摻雜的ZGNR的結構是穩定的,且在P5位置摻雜最穩定.該研究對于發展基于石墨烯的納米電子器件很有意義.

[1]Novoselov K S,Geim A K,Morozov S V,Jiang D,Zhang Y,Dubonos S V,Grigorieva I V,Firsov A A 2004Science306 666

[2]Barone V,Hod O,Scuseria G E 2006Nano Lett.6 2748

[3]Yang L,Park C H,Son Y W,Cohen M L,Louie S G 2007Phys.Rev.Lett.99 186801

[4]Hod O,Barone V,Scuseria G E 2008Phys.Rev.B77 035411

[5]Wang D,Zhang Z H,Deng X Q,Fan Z Q 2013Acta Phys.Sin.62 207101(in Chinese)[王鼎,張振華,鄧小清,范志強2013物理學報62 207101]

[6]Farzaneh S 2015J.Phys.Chem.C119 12681

[7]Wang Q H,Shih C J,Paulus G L C,Strano M S 2013J.Am.Chem.Soc.135 18866

[8]Kan Z,Nelson C,Khatun M 2014J.Appl.Phys.115 153704

[9]Zhu Z,Zhang Z H,Wang D,Deng X Q,Fan Z Q,Tang G P 2015J.Mater.Chem.C3 9657

[10]Yu Z L,Wang D,Zhu Z,Zhang Z H 2015Phys.Chem.Chem.Phys.17 24020

[11]Zhang W X,He C,Li T,Gong S B 2015RSC Adv.5 33407

[12]Tang G P,Zhang Z H,Deng X Q,Fan Z Q,Zhu H L 2015Phys.Chem.Chem.Phys.17 638

[13]Zhang H L,Sun L,Wang D 2016Acta Phys.Sin.65 016101(in Chinese)[張華林,孫琳,王鼎 2016物理學報65 016101]

[14]Zhao S Q,Lü Y,Lü W G,Liang W J,Wang E G 2014Chin.Phys.B23 067305

[15]Liu J,Zhang Z H,Deng X Q,Fan Z Q,Tang G P 2015Org.Electron.18 135

[16]Xiao J,Yang Z X,Xie W T,Xiao L X,Xu H,Ouyang F P 2012Chin.Phys.B21 027102

[17]Liu Z M,Zhu Y,Yang Z Q 2011J.Chem.Phys.134 074708

[18]Xu B,Lu Y H,Feng Y P,Lin J Y 2010J.Appl.Phys.108 073711

[19]Manna A K,Pati S K 2011J.Phys.Chem.C115 10842

[20]Menezes M G,Capaz R B 2012Phys.Rev.B86 195413

[21]He J,Chen K Q,Fan Z Q,Tang L M,Hu W P 2010Appl.Phys.Lett.97 193305

[22]Seol G,Guo J 2011Appl.Phys.Lett.98 143107

[23]Ci L J,Song L,Jin C H,Jariwala D,Wu D X,Li Y J,Srivastava A,Wang Z F,Storr K,Balicas L,Liu F,Ajayan P M 2010Nat.Mater.9 430

[24]Hu R,Fan Z Q,Zhang Z H 2017Acta Phys.Sin.66 138501(in Chinese)[胡銳,范志強,張振華2017物理學報66 138501]

[25]Zhang Z,Zhang J,Kwong G,Li J,Fan Z,Deng X,Tang G 2013Sci.Rep.3 2575

[26]Zhang Z H,Guo C,Kwong D J,Li J,Deng X Q,Fan Z Q 2013Adv.Funct.Mater.23 2765

[27]Kan M,Zhou J,Sun Q,Wang Q,Kawazoe Y,Jena P 2012Phys.Rev.B85 155450