基于點擊流的用戶矩陣模型相似度個性化推薦

,,

(湖南大學 a.信息科學與工程學院;b.可信系統與網絡實驗室,長沙410082)

0 概述

為了能夠讓用戶在智慧校園[1]學習平臺取得更高的學習效率,智慧校園平臺學習資源按照學部、年級和科目分類,便于學生檢索,提高學習效率。據統計,平均每天有上十萬的用戶登錄智慧校園學習平臺進行學習,每天能夠產生上百萬條學習資源類別的點擊流[2]數據。如何分析用戶的海量點擊流數據挖掘用戶感興趣的學習資源,對用戶進行個性化推薦[3]是一個極具挑戰性的工作。

用戶對學習資源評價和學習資源搜索記錄主觀的網絡行為,能夠反映用戶對學習資源的興趣,所以大部分學習網站分析學習資源評價內容和學習資源搜索記錄,挖掘用戶的興趣,從而給用戶進行資源推薦[4]。雖然這種基于內容的推薦具有直接而準確的優點,但是推薦之前需要進行大量的內容分析工作,涉及到網頁特征的抽取以及所使用的語言的語法、語意、詞法的分析等[5]。這種推薦算法不僅工作量巨大,而且當用戶訪問歷史時間較短時,對該用戶的訪問內容分析也難以得到正確的結果,因此基于內容推薦算法具有一定的局限性。

研究學者發現用戶在瀏覽網頁資源過程中所產生的點擊流信息可以從側面反映出用戶的興趣,該研究結果在智慧校園學習資源網站同樣適用。用戶瀏覽學習資源會產生資源類別的點擊頻率、點擊路徑以及在某一資源類別下的停留時間等點擊流數據[6],但是由于視頻學習資源的時間長短不一,因此頁面停留時間不能有效衡量用戶對該類學習資源的興趣。同時用戶在學習的過程中對學習資源的喜好程度也會跟隨時間產生變化,所以,引入時間遺忘因子[7]評估用戶對學習資源的興趣程度很有必要。本文針對智慧校園APP學習資源網站特定的網絡環境,為用戶個性化推薦學習資源做了大量的實驗與研究。

1 相關工作

1.1 點擊流數據相關研究

近年來國內外學者關于用戶網頁點擊流信息挖掘用戶興趣,求解相似用戶,為用戶進行個性化資源推薦已經具有了一定的研究成果。用戶點擊流信息的研究涉及到學習資源網站、電商網站、旅游網站等領域,文獻[8]挖掘用戶網頁點擊流記錄構建了用戶在線購物模型,預測用戶網頁購買行為;文獻[9]研究了大型商務網站用戶點擊流信息挖掘用戶興趣為用戶進行商品個性化推薦,深入分析了用戶網頁商品類目的點擊頻率、點擊路徑和網頁頁面停留時間3種用戶點擊流信息構建用戶推薦模型,取得了一定的效果,但是這篇文章中求解用戶相似度算法時間復雜度太高且推薦效率不是很理想。

1.2 聚類算法分析

用戶聚類是用戶個性化推薦的第一步,目前相當成熟的用戶聚類算法有多種。K-means算法[10]是最常用的聚類算法之一,其算法時間復雜度較低,但是對樣本的輸入順序敏感,可能產生局部最優解,而且受孤立點的影響很大。 K-medoids算法[11]是另一種常用的聚類算法,該算法雖然能在一定程度上控制異常數據的影響,但是其時間復雜度較高,在海量用戶點擊流數據的情況下求解相似用戶,效率低下。基于這些問題,研究學者提出了一種領導聚類(Leader Clustering)算法,這種算法不需要預先指定分類對象的簇中心點,而是在簇中隨機指定一個對象作為leader,然后計算數據集中所有對象與leader的距離,若距離值小于閾值,則將該對象指派給該leader,否則該對象作為一個新的leader。這樣只需要遍歷一次數據集就可以對所有對象進行分類,時間復雜度較低。但是對于具有大量對象的數據集,一個對象有可能歸于多個類,因此,研究學者又提出了粗糙集理論[12]來解決這個問題。粗糙集理論中每一個簇有一個上近似集和一個下近似集,所以,當某一個對象不確定歸屬于哪一個簇的時候,可以采用上近似集和下近似集的概念將該對象指派為至少一個確定的簇。

基于上述考慮,本文提出了JMATRIX算法,將智慧校園用戶歷史資源點擊流數據,構建用戶資源類別點擊數據有向圖模型,并將資源類別有向圖模型轉化為矩陣模型存儲,然后設計用戶相似度求解公式,克服稀疏矩陣冷啟動問題[13],求解矩陣模型相似度從而求得用戶相似度,最后JMATRIX算法結合Leader Clustering算法及粗糙集理論思想,為用戶進行個性化資源推薦。實驗結果表明,JMATRIX算法極大的提高了用戶的聚類效率和用戶相似度準確性,證實了JMATRIX算法相比其他推薦算法在用戶個性化學習資源推薦領域具有較高的效率和準確性。

2 基于JMATRIX算法用戶相似度求解

JMATRIX算法用戶相似度求解思想如下,先根據智慧校園APP學習網站結構創建用戶資源點擊數據有向圖模型,并且引入遺忘因子對用戶資源點擊數據有向圖模型進行遺忘,及時更新有向圖模型每一條有向邊的權值。根據最終的用戶資源點擊數據有向圖模型構建用戶資源點擊數據矩陣模型,然后通過JMATRIX算法用戶相似度求解公式求得用戶資源點擊數據矩陣模型的相似度,從而求得用戶的各興趣指標相似度。

2.1 學習資源網站結構

智慧校園APP學習網站具有豐富的學習資源,其樹型結構如圖1所示。其中第一級父節點為資源類型(如優課),每一個父節點下面又可以分為多個一級子節點(如年級),每一個一級子節點下面分為多個二級子節點(如科目),且一級子節點為二級子節點的父節點,依次類推,每一個二級子節點下面分為多個三級子節點(如教材版本)。

圖1 智慧校園APP學習網站結構

2.2 用戶興趣指標

本文引入時間遺忘因子,根據時間賦予資源類別點擊頻率和資源類別點擊路徑2個指標不同的權值,計算用戶的相似度。常用的用戶資源類別點擊頻率相似度求解算法復雜度較高,通過計算用戶每一次會話訪問每一個資源類別及資源類別下資源點擊數,與本次會話中所有資源點擊總數求商,得到每一個資源類別的點擊頻率。然后取某段時間內資源類別點擊頻率平均值,構造資源類別的點擊頻率用戶矩陣,通過求解資源類別頻率用戶矩陣中用戶資源類別點擊頻率向量相似度,求得用戶資源類別點擊頻率相似度。常用的資源類別訪問路徑的相似度求解,通過求解一段時間內用戶之間每一條資源訪問路徑交集與資源路徑的并集求商,得到用戶之間每一條資源訪問路徑的相似度,取平均值來求得用戶的資源訪問路徑的相似度,該求解方式不僅時間復雜度高,而且會丟失精度[14]。為了克服以上問題,本文基于用戶歷史資源類別點擊流信息,構建了用戶資源類別點擊數據有向圖模型,并將資源類別有向圖模型轉化為矩陣模型存儲,設計獨特的矩陣模型相似度求解公式求解用戶矩陣模型相似度,不僅可以一次求得用戶的資源類別點擊頻率和資源類別點擊路徑的相似度,極大地簡化了用戶相似度的求解過程,而且克服了稀疏矩陣的冷啟動問題,提高算法的通用性和準確性,取得了非常理想的用戶相似度結果。

2.3 用戶相似度求解

本文用戶相似度求解方式如下,如例用戶P一次會話的資源類別訪問路徑:A-B-D-E-B-D(其中,A、B、C、D、E代表不同的資源類別),那么該條資源類別點擊數據在有向圖中的存儲如圖2所示,資源類別之間每一條有向邊代表用戶點擊資源類別的跳轉路徑,每一條有向邊的權值代表用戶資源類別之間的跳轉次數,可以根據資源類別之間跳轉次數與跳轉總次數求商,得到資源類別之間的跳轉頻率。因此資源有向圖同時存儲了用戶資源類別點擊頻率和資源類別訪問路徑的點擊流信息。

圖2 用戶P某條資源類別點擊數據有向圖模型

資源類別點擊頻率和資源類別訪問路徑是根據用戶資源點擊記錄,獲取資源所屬的類別點擊信息而得到的,如果學習資源同時屬于多個資源類別,那么進行該資源點擊信息歸屬的類別需要做如下處理,例如資源訪問路徑:resource1(二年級|語文|湘教版)-resource2(二年級|數學|湘教版)-resource3(三年級|英語),則權值二年級-三年級=1/3×1/3=1/9。同理,二年級-數學、二年級-湘教版、語文-二年級、語文-數學、語文-湘教版、湘教版-二年級、湘教版-數學、湘教版-湘教版權值均為1/9。二年級-三年級=1/3×1/2=1/6,同理得到二年級-英語、數學-三年級、數學-英語、湘教版-三年級、湘教版-英語權值均為6/1。

人類的自然遺忘是一個漸進的過程,因此,可以推斷用戶對某一事物的興趣也遵循這一規律,即用戶的興趣也隨著時間的推移而減弱,而且興趣遺忘的速度也是按照時間順序先快后慢。用戶最近多次訪問的學習資源最能代表用戶最近的興趣,通過引入遺忘因子對用戶的興趣逐漸遺忘,給用戶每一條資源類別的訪問信息賦予修正權值,得到合理的用戶點擊記錄模型。

遺忘因子K計算公式如下:

(1)

其中,cur表示當前日期,time表示用戶瀏覽資源類別的日期,h表示興趣遺忘半衰期,即經過h天后用戶的興趣非線性遺忘了一半,它遺忘的速度先快后慢。h的值可以根據實驗結果反復調試,也可以依據理論知識人為設定,遺忘速度的快慢由h直接控制。根據艾濱浩斯曲線[15]遺忘規律2 d的時間可以讓人類對事物的遺忘達到72%,綜合用戶對學習資源興趣的遺忘場景考慮,本文半衰期h定義為2天。

得到時間遺忘因子K值之后,將用戶某段時間內對資源類別的每條訪問路徑均賦予一個遺忘因子K值。如用戶P一次會話的資源類別訪問路徑:A-B-D,將本條路徑賦予遺忘因子K值,則可以得到本次資源類別訪問路徑為K(A-B-D)。若代入相關參數求得K=0.5,則資源類別A跳轉至資源類別B,資源類別B跳轉資源類別D,由原來的1次變為0.5次,所以,最終本條路徑在資源類別點擊數據有向圖中的有向邊權值為0.5。

基于以上原理,將一段時間內用戶對學習資源類別點擊頻率、訪問路徑的點擊流信息轉化為有向圖模型存儲,如圖3所示。

圖3 用戶某段時間資源類別點擊數據有向圖模型

然后建立學習資源類別矩陣模型,將用戶學習資源類別點擊流信息存儲圖轉化為學習資源類別矩陣模型存儲,如下:

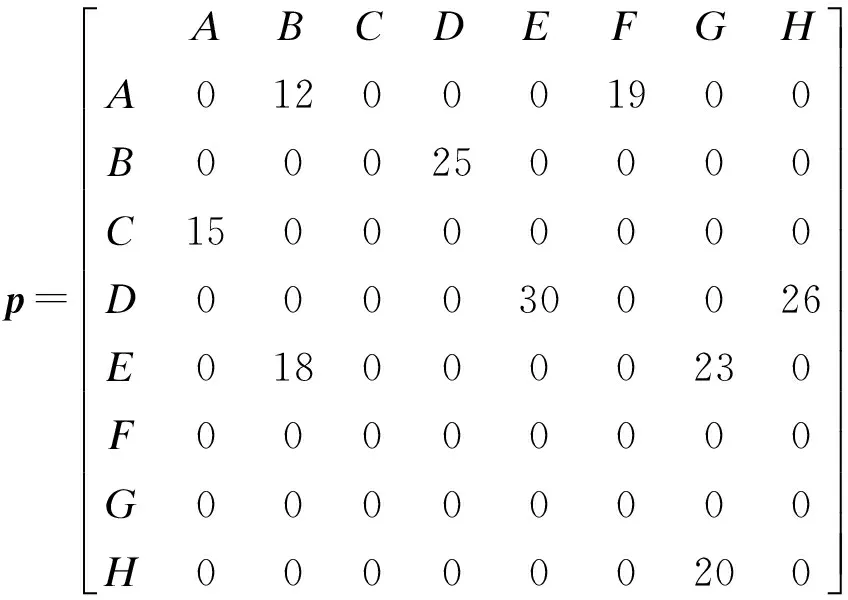
因此,可以求解用戶之間學習資源類別矩陣相似度從而求得2個用戶之間的相似度,矩陣相似度求解公式如下:

(2)

其中,pi代表p矩陣第i行向量,qi代表q矩陣第i行向量,Spi代表p矩陣第i行點擊總數,Sqi代表q矩陣第i行點擊總數,Sp代表p矩陣總點擊總數,Sq代表q矩陣總點擊總數。依次求解2個用戶點擊流數據矩陣每一行向量用戶相似度,選取2個矩陣中所對應的每一行點擊數據頻率的最小值作為該行的權值,然后與每一行向量用戶相似度求積,再將所得行向量的相似度求和,得到2個用戶之間的相似度。選取每一行點擊數據頻率最小值作為該行的權值可以克服稀疏矩陣引起計算誤差,當某一行向量全部為0或者2個矩陣對應的2個行向量為零時,零向量將會忽略,所以,該由零向量引起的稀疏矩陣冷啟動問題也會得到解決。

對于(n×m)的資源類別點擊數據矩陣模型用戶p,q相似度求解具體的計算公式如下:

(3)

3 實驗分析與驗結果

3.1 基于JMATRIX算法個性化推薦流程

JMATRIX算法結合Leader Clustering算法和粗糙集理論進行用戶個性化推薦,不僅能夠對大量的用戶進行快速有效聚類,還能夠針對一個用戶同時屬于多個分類的問題,引用粗糙集理論進行有效聚類處理。JMATRIX算法在簇中隨機指定一個對象作為leader,然后根據JMATRIX算法用戶相似度計算方法,計算數據集中所有對象與領導集中leader的用戶相似度,若用戶相似度小于所設定的用戶相似度與閾值α,該對象作為一個新的領導返回到領導集中,否則判斷用戶相似度與該用戶和領導集中所有leader的最大用戶相似度之商,是否大于或等于粗糙集閾值β,如果滿足條件那么將該對象指派給這個leader。因此,引用粗糙集理論可以有效解決一個對象滿足條件有可能歸于多個聚類的問題。JMATRIX算法流程如圖4所示。

圖4 JMATRIX算法流程

3.2 實驗數據集

通過智慧校園用戶學習資源點擊記錄的日志數據,提取日志數據進行預處理,對用戶訪問極少的學習資源類別和訪問數據極少的用戶進行過濾處理,提高數據集質量。用戶智慧校園學習資源類別點擊流數據集如表1所示。

表1 實驗數據集

3.3 JMATRIX算法參數優化

JMATRIX算法具有用戶相似度閾值和粗糙集閾值2個閾值,2個閾值的大小會影響到聚類結果。用戶與leader之間的相似度超過了用戶相似度閾值,則說明該用戶可能歸屬于該leader,而粗糙集閾值則決定了某一個用戶是否能夠同時歸屬于多個leader。如果用戶相似度閾值設置過低,那么無關的用戶會指派給leader產生誤差,用戶相似度閾值設置過高,那么用戶會因為過高的用戶相似度閾值而難以歸屬于某一個聚類,從而形成較多的聚類。如果粗糙集閾值設置過低,將會產生不合理的聚類重疊,如果粗糙集閾值設置過高,將會難以使得相似度高的用戶歸為一個聚類,從而形成過多的冗余聚類。因此,需要根據實驗結果調整參數進行反復實驗。

去掉粗糙集閾值的限制條件,根據用戶相似度閾值參數調整進行反復實驗,實驗結果如圖5所示,用戶相似度閾值從0.1增至0.2,用戶聚類數沒有太大的變化,因為用戶相似度閾值過低,會使得一個用戶聚類包含眾多與聚類領導相差甚遠的對象。用戶相似度閾值從0.2增至0.35,用戶聚類數會隨著用戶相似度閾值的增大而增加,當用戶相似度閾值達到0.4之后,用戶聚類數隨著用戶相似閾值的增加而急速增加,且形成了過多的不具有代表性的用戶聚類。綜合考慮8 040個用戶和45個資源分類,用戶相似度閾值取0.3,將用戶分為24個聚類。本領域其他研究成果顯示,用戶相似度閾值設置在0.2～0.3較為合適。

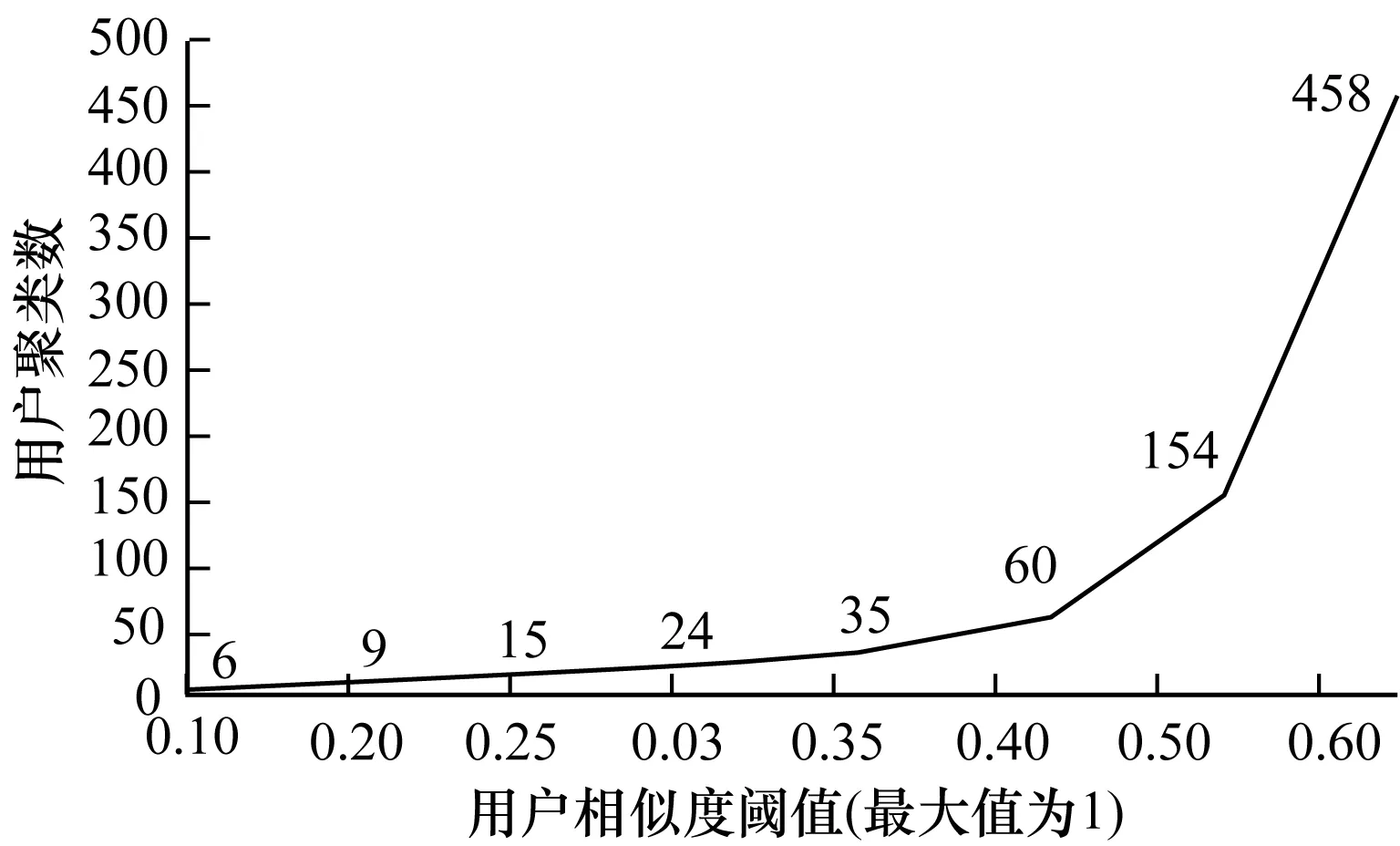
圖5 用戶聚類數隨用戶相似度閾值變化曲線

為了確定合適的粗糙集閾值,根據所取的用戶相似度閾值0.3,不斷調整用戶粗糙集閾值的大小,得到聚類平均用戶數結果如圖6所示。去掉粗糙集限制條件,用戶相似度閾值取0.3,則聚類平均用戶數為335個。由實驗結果圖可以看出,粗糙集閾值由0.7下降到0.4時,聚類中會產生過多的重復用戶,且粗糙集閾值越小,重復用戶數越多,當粗糙集閾值由0.85增至0.9時,平均用戶數緩慢下降,且當粗糙集閾值達到0.9時,平均用戶數接近335個,聚類中幾乎不會產生重復用戶。所以,綜合分析得到粗糙集閾值取0.7～0.85較為合適。而且當用戶相似度閾值取0.3,調整粗糙集閾值的大小,得到JMATRIX算法的準確率與召回率,實驗結果如圖7所示。粗糙集閾值從0.4增至0.6,準確率有小幅的提升,當粗糙集閾值從0.6增至0.8,準確率有大幅度提升且在粗糙集閾值為0.8時準確率達到最大值,當粗糙集閾值大于0.8,準確率會隨之降低。召回率在粗糙集閾值處于0.4至0.9之間小幅波動,并無太大變化。綜合分析得到,用戶相似度閾值取0.3,粗糙集閾值取值0.8最優。

圖6 聚類平均用戶數隨粗糙集閾值變化曲線

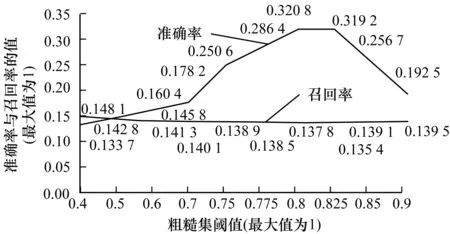
圖7 準確率、召回率隨粗糙集閾值變化曲線

3.4 結果分析

根據上面的結果分析,將用戶相似度閾值取值0.3,粗糙集閾值取值0.8,基于相同的實驗數據集,針對JMATRIX算法、Rough Leader Clustering算法和K-medoids算法3種推薦算法進行實驗,所得算法用戶聚類數、運行時間結果如圖8所示,所得算法準確率、召回率如圖9所示,實驗結果顯示,JMATRIX算法在運行效率上相比Rough Leader Clustering算法和K-medoids算法分別提高了15%和29.17%,JMATRIX算法在推薦的準確率上相比Rough Leader Clustering算法和K-medoids算法分別提高了15.35%和24.2%,JMATRIX算法在推薦召回率上相比Rough Leader Clustering算法和K-medoids算法分別提高了16.48%和26.89%。由此可以得到,本文提出的JMATRIX算法在運行時間、準確率和召回率等指標上相比Rough Leader Clustering算法和K-medoids算法更優,因此驗證了JMATRIX算法基于用戶點擊流數據在用戶個性化推薦上具有更高的效率和更精確的推薦效果。

圖8 3種算法運行時間、用戶聚類數結果

圖9 4種算法準確率、召回率結果

4 結束語

本文基于智慧校園APP用戶不同類別的學習資源點擊流數據,提出JMATRIX算法。引入時間遺忘因子,根據時間賦予資源類別點擊頻率和資源類別點擊路徑2個指標不同的權值,構建用戶學習資源類別點擊流數據有向圖模型,并將學習資源類有向圖模型轉化為矩陣模型存儲,設計矩陣相似度求解公式,克服稀疏矩陣零向量引起的冷啟動問題,求解用戶相似度。JMATRIX算法極大地簡化用戶相似度求解過程,降低了算法的時間復雜度,提高了用戶相似度求解效率和用戶相似度準確性。實驗結果證明,JMATRIX算法相比其他推薦算法具有更高的效率和準確性。下一步工作將研究JMATRIX算法的鄧恩指數等其他推薦算法指標的優劣,以及研究JMATRIX算法在電商網站等領域的推薦效果。

[1] 胡欽太,鄭 凱,林南暉.教育信息化的發展轉型:從“數字校園”到“智慧校園”[J].中國電化教育,2014(1):35-39.

[2] 劉 嘉,祁 奇,陳振宇.ESSK:一種計算點擊流相似度的新方法[J].計算機科學,2012,39(6):147-150.

[3] 印 鑒,王智圣,李 琪.基于大規模隱式反饋的個性化推薦[J].軟件學報,2014(9):1953-1966.

[4] 朱 亮,陸靜雅,左萬利.基于用戶搜索行為的Query-doc關聯挖掘[J].自動化學報,2014,40(8):1654-1666.

[5] 梁邦勇,李涓子,王克宏.基于語義Web的網頁推薦模型[J].清華大學學報(自然科學版),2004,44(9):1272-1276.

[6] 何 躍,馬麗霞,騰格爾.基于用戶訪問興趣的Web日志挖掘[J].系統工程理論與實踐,2012,32(6):1353-1361.

[7] 朱國瑋,周 利.基于遺忘函數和領域最近鄰的混合推薦研究[J].管理科學學報,2012,15(5):55-64.

[8] MOE W W.An Empirical Two-stage Choice Model with Varying Decision Rules Applied to Internet Clickstream Data[J].Journal of Marketing Research,2006,43(4):680-692.

[9] SU Qiang,CHEN Lu.A Method for Discovering Clusters of E-commerce Interest Patterns Using Click-stream Data[J].Electronic Commerce Research & Applications,2015,14(1):1-13.

[10] HARTIGAN J A,WONG M A.A K-means Clustering Algorithm[J].Applied Statistics,2013,28(1):100-108.

[11] PARK H S,JUN C H.A Simple and Fast Algorithm for K-medoids Clustering[J].Expert Systems with Applications,2009,36(2):3336-3341.

[12] PARMAR D,WU T,BLACKHURST J.MMR:An Algorithm for Clustering Categorical Data Using Rough Set Theory[J].Data & Knowledge Engineering,2007,63(3):879-893.

[13] 廖壽福,林世平,郭 昆.個性化推薦冷啟動算法[J].小型微型計算機系統,2015,36(8):1723-1727.

[14] 于 洪,羅 虎.一種Web用戶訪問路徑的可能性模糊聚類算法[J].小型微型計算機系統,2012,33(1):135-139.

[15] ZENG Liren,LI Ling.An Interactive Vocabulary Learning System Based on Word Frequency Lists and Ebbinghaus’Curve of Forgetting[C]//Proceedings of Workshop on Digital Media & Digital Content Management.Washington D.C.,USA:IEEE Press,2011:313-317.