基于高維數據流的異常檢測算法
,,
(蘇州大學 計算機科學與技術學院,江蘇 蘇州 215006)
0 概述
異常檢測旨在從數據集中快速有效識別異常點,在金融數據分析、網絡安全、醫學疾病與藥物分析領域被廣泛應用。基于無線傳感網和GPRS技術,對物理世界進行感知,則是數據挖掘異常檢測領域又一重要研究方向[1]。傳統的異常檢測算法主要分為基于統計的異常點檢測算法、改進的基于距離的異常點檢測算法、基于密度的局部異常點檢測算法[2],它們主要基于統計學理論,以歐氏距離作為異常評判標準。
基于傳感器技術的數據挖掘能從大量、模糊的復雜數據中提取出潛在的、有價值的信息,而且傳感器網絡數據多以高維形式存在,具有海量、異構有噪聲、實時要求性高等特性,這使得傳統的數據分析算法檢測出異常點的效果不明顯,而且時間復雜度過高,具有潛在的局限性。高維數據流的異常檢測面臨較多的挑戰。
國內外已有大量的學者針對無線傳感網的數據挖掘進行相關研究并提出一系列方法用于高維數據流的異常檢測。如文獻[3]采用K-means算法思想,比較傳感器節點采集的數據點的相似度并劃分聚類,根據數據點與聚類中心的距離區分正常數據與異常數據,但該方法采集的數據點維數有限,不適合高維數據的檢測。文獻[4]提出采用基于模式的聚類算法,分段取模式特征,并結合K最近鄰算法計算局部異常因子。文獻[5]提出一種快速數據流離群點檢測算法FODFP-Stream,通過動態發現和維護頻繁模式來計算高維類別屬性數據點離群度實現快速有效檢測,但針對數值屬性和混合屬性數據的異常檢測缺乏一定的擴展性。
針對高維空間下的異常點檢測,文獻[6]提出基于角度的異常檢測算法(Angle-based Outlier Detection,ABOD)[6]。在高維空間中,角度比距離更穩定,余弦角度方差一定程度上可以反映數據的異常度[6-7]。在此基礎上,文獻[8]提出了HODA算法,定義了方差異常因子和網格密度等相關概念,通過降維和網格劃分處理數據集,最后根據剩余的網格計算異常因子ABOF。雖然該算法準確率較高,但是算法時間復雜度仍較高。
高維數據流是連續的時間序列值,正常情況下在一定范圍內出現小幅度的波動。某一異常點的出現與上一條數據存在一定的偏差,或者從某一時間序列開始,數據點偏離最佳數據集[9]。針對高維數據流的這一特點,本文提出一種改進的基于角度方差的數據流異常檢測算法。該算法根據采集的高維數據流特點,利用網格劃分出最佳數據集網格和最近數據集網格提高算法的運行效率。
1 問題描述及相關定義
下面簡要介紹相關知識:
定義1假設高維數據流是一種K元關系R={rt|rt∈S,t=1,2,…},其中,元組rt(t=1,2,…)連續到達[10],t為該數據點到達時間,K為數據的維度。
定義2假設給定一種Rd空間上的數據集S={X1,X2,…,Xi,…,Xn}以及一個樣本點Xp∈S,隨機選擇一對樣本點Xm,Xn∈S{Xp},θmpn為向量mp與pn的角度,所有θmpn的角度方差值為:
VOAp=Var[θmpn]=MOA2(p)-(MOA1(p))2
(1)
其中:
(2)
(3)
定義3最佳數據集網格是數據流的小規模數據流型。在數據空間中,由角度方差在閾值μ內的數據點被且標記為正常數據的數據點組建成網格。
基于物聯網技術采集的數據流采集可以感知電梯運行整體狀況。電梯數據流模型中有實時狀態數據和維保特征、運行特征等,數據來源更豐富,潛在高階特征多,更全面地反映電梯運行健康狀況:
1)電梯基本特征包含了電梯基本信息,包括電梯使用年限和已使用年限、額定速度等。
2)電梯維保特征是電梯維保狀況的重要體現,如電梯維保頻次、平均維保時間等。
3)電梯運行特征主要包括當月故障次數、困人次數和用戶投訴情況等。
4)電梯機械節點實時狀態,這是電梯特征中最關鍵的特征。以傳感器和通信技術為基礎,感知電梯各重要機械節點的實時運行狀態。
2 改進的高維數據流異常檢測算法
本文利用數據集網格劃分加快了ABOD算法的計算,同時通過實時更新網格的機制保證數據檢測精度;基于此,針對電梯狀態數據先進行預處理,對數據屬性進行篩選,其次將本文改進算法運用于電梯數據流的異常分析。
實時數據流的檢測需要算法具有較好的及時性和準確性。本文改進算法的主要思想為:根據數據分布對數據流進行劃分,文獻[8]通過對所有的數據點進行網格劃分來過濾正常區域,但這一方法未考慮數據流的概念轉移問題,在本文算法的執行過程中,實時維護一個最佳數據網格和最近數據網格,據此對最新采集的高維數據計算角度方差異常因子,使得歷史數據流中部分數據參與角度方差因子的計算,計算代價小,滿足實時性要求;對于算法檢測出的異常點,分析導致數據異常的主要屬性,確保算法對數據異常屬性的識別能力。
如圖1所示,計算正常網格和候選網格中數據點的異常因子,HODA算法認為角度方差異常因子小于閾值的數據點為異常點。
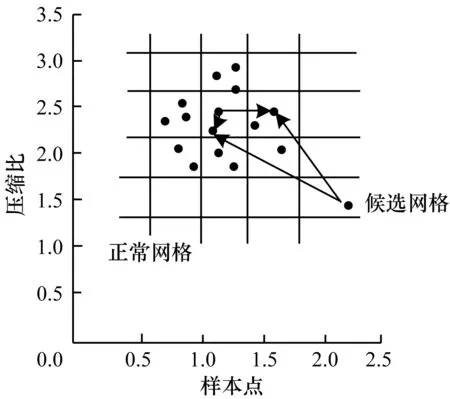
圖1 數據點角度方差
算法高維數據流異常檢測
輸入最佳數據網格閾值μ,最佳數據網格尺度BL,最近數據網格尺度RL
輸出異常數據集S
1.Best_grid→?,Latest_grid→?
2.for inputXiFrom Datastream,init grids
3.for all Diin best_grid,calculate the XiVOA
4.for allFiin Latest_grid,calculate the XiVOA
5.calculate the averageVOA according to the above VOA value.
6.if VOA of Xi<μ,label Xias normal
7.if number of Di>BL,dequeue the first record
8.else Di=DiU {Xi}
9.if number ofFi>RL,dequeue the first record
10.else Fi=FiU {Xi}
11.else S=S U {Xi}
12.end
其中,步驟3、步驟4是算法的核心步驟,以上步驟的流程如圖2所示。
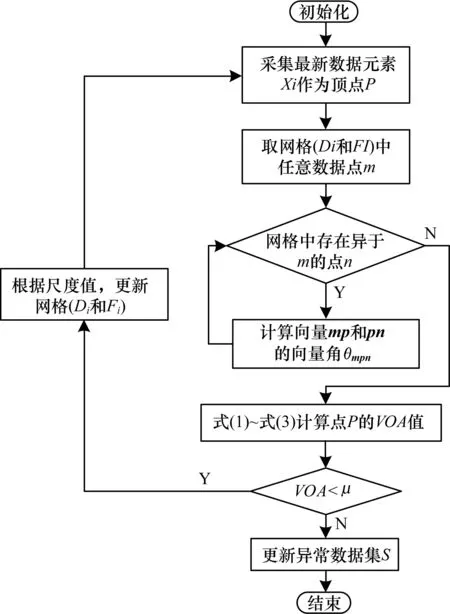
圖2 算法流程
為使算法運行效率更高,在計算角度方差異常因子之前,算法先由樣本值和最佳數據網格閾值篩選出最佳數據集區域。最佳數據集網格劃分閾值是一個關鍵參數。在取不同值時,最佳數據網格抽象的結果相差很大。當過大時,網格劃分粒度過大,網格中數據增加,從而加大了計算量,算法優化效果不明顯。反之,當過小時,最佳數據集代表性不強。此時,雖然計算效率提高,但聚類效果也明顯下降。
最佳數據集閾值μ、最佳數據集尺度BL和最近數據集尺度RL是影響算法精度的主要因素,而且不同的尺度和閾值對應于不同的算法精度。為了獲得最優的尺度和閾值,算法需要進行大量的實際測試。一般而言,每種應用產生的數據集對應于一定的規律與特性,同時也對應了一組最優的權值和閾值[11]。大量實驗結果表明,只要獲得一組與數據集對應的最優權值和閾值,算法即可以獲得較高的準確性。
3 基于改進算法的電梯異常數據檢測
3.1 數據預處理
在高維數據流分析中,如何從大量復雜原始特征中去除影響因子小的相關特征,提取關鍵特征,對于提高檢測精度和效率必不可少[12]。
1)RTS特征
傳感器采集的電梯各機械部位實時特征在4大數據源中所占比重最大,也是最有價值的特征值。在本文項目中,通過傳感器技術可以采集到的電梯特征值如圖3所示,同一時刻采集電梯共19維特征。
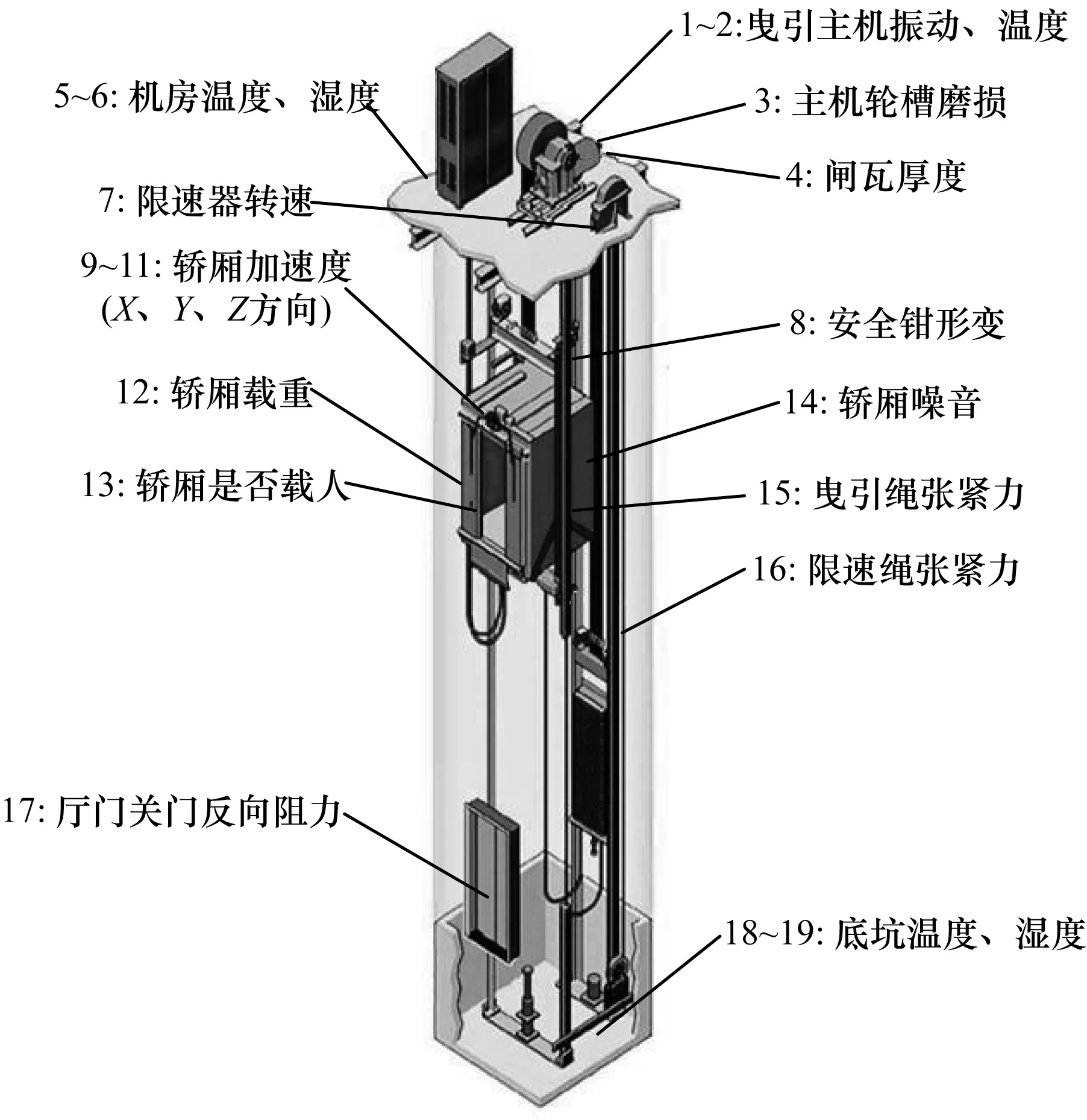
圖3 電梯各部位實時特征值
2)MTS特征
維保特征是電梯檢修和維護狀態的體現。本文選擇了比較重要的維保周期、維保項目、平均維保時長和維保滿意程度等4個特征。
3)FD特征
電梯基本特征是對電梯主要特征的描述。根據關鍵質量指標[13]選擇了額定載重、電梯層站門數、折余價值和日平均使用時間等4個關鍵特征。
4)RTD特征
電梯運行特征是指電梯故障統計特征,包括過去一周電梯故障次數、困人次數、被投訴次數和工單派發次數等,這是電梯重要異常特征歷史值。
其中,RTS是無線傳感網采集的電梯各關鍵部位實時數據流,后3類特征值是較為穩定的電梯特征值,以周為單位進行統計查詢得到相關特征。
電梯部分狀態特征如表1所示。

表1 電梯部分狀態特征
3.2 電梯高維數據流異常檢測
由于電梯數據包括實時數據流和維保特征、基本特征等較為穩定的數據值,本文將采集的電梯實時數據流進行初始化,將電梯實時狀態數據Xi作為輸入:
1)統計查詢電梯本周的MTS、FD、RTD等特征值,并進行預處理。
2)實時采集數據流,獲得一定的高維數據集樣本,根據樣本值和最佳數據集閾值進行初始化,從而構造初始最佳數據網格和最近數據網格。
3)傳感器網絡采集的即時狀態數據Xi和小規模數據流型計算集實時計算該數據點的VOA值。
4) 基于VOA值和設定的最佳數據集閾值判斷最新數據點的異常情況。
5)若為異常點,則納入異常數據集并計算異常屬性,分析導致異常的維度;若為非異常點,則按照先進先出法和最近數據集網格尺度對最近數據集網格進行更新。
4 實驗結果與分析
本文方法采用的實驗環境為計算機Intel(R) Core(TM) i5-3470 CPU @ 3.20 GHz,內存8.0 GB。開發平臺為PyCharm 2015,采用Python語言和pandas等分析包對本文改進的算法和HODA算法進行比較,并對電梯運行狀態的真實數據進行檢測。
本文采用運行時間和準確率作為算法的評價指標[14],準確率是用來衡量算法的精度。
p=o/c
(4)
其中,o表示預測異常點集中真實異常點個數,c為算法檢測到的異常點總數。
實驗1采用入侵檢測數據集KddCup99[15]作為測試數據集。該數據集具有高維的特性,這里分別選擇其中的1 000條、 2 000條、3 000條、5 000條數據,其中異常記錄為25條。
本文采用KddCup99數據集分析算法的及時性和有效性,進行以下實驗:設置參數最優數據網格閾值μ為0.3,最佳數據集尺度BL為50,最近數據集尺度RL為30;采用ABOD算法、HODA算法與本文算法進行對比,其中HODA算法與本文算法的實驗結果如表2、圖4所示。

表2 2種算法實驗結果分析
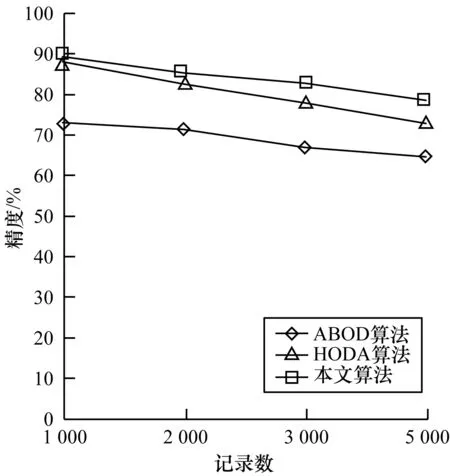
圖4 不同算法精度對比
針對實驗數據集,從表2和圖4可以看出,當實驗數據集增大時,在算法運行時間上,本文算法比HODA算法更有優勢,原因在于HODA算法在計算異常因子時會重新分配數據網格,算法的計算復雜度加大。3種算法精度都呈下降趨勢,但是相比HODA算法本文算法實驗獲得的最優參數能夠保證對高維數據異常狀態的識別能力,相比HODA算法保持較高的精度。
實驗2使用昆山市某電梯公司2016年4月—2016年5月物聯網平臺數據作為實驗數據來源,分布于電梯各機械部位的無線傳感器節點,將采集到的電梯狀態數據通過GRRS發送到服務器,其數據采集頻率為2 s一次。
圖5是2種算法在不同時刻的運行時間對比,隨著電梯高維數據流的陸續到達,算法數據規模呈指數增長,可以看出本文異常檢測算法運行所消耗時間均小于相同數據規模下的HODA算法。因為HODA算法在計算角度方差異常因子時需要實時對網格進行劃分后篩選出候選網格,而本文算法維護2個最具代表的網格數據集,數據規模越大本文算法在其運行時間上的優勢越明顯。
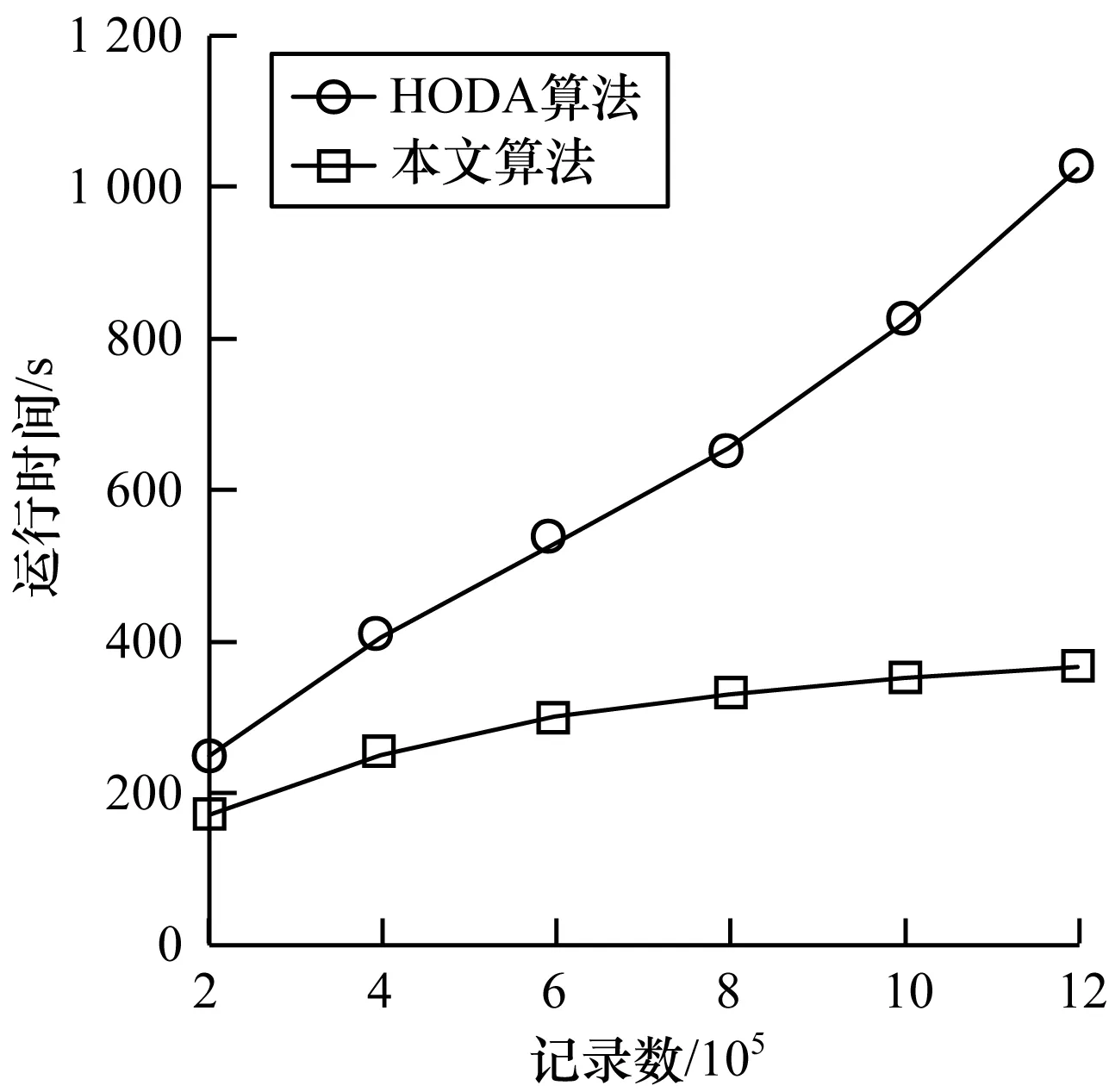
圖5 電梯異常數據檢測時間
查準率采用被檢測出的實際異常點數目與檢測到可疑異常點數目之比進行度量。實驗過程中電梯產生12次不同程度的異常事件,根據圖6中2種算法平均查準率的對比可知,本文算法的查準率要優于HODA算法。這是因為對于數據流中的最新數據點HODA算法需要重新進行網格劃分,當數據集規模較大、維數較高時,該方法的候選網格增多,會將較多非異常的數據誤以為是異常狀態值。且本文算法采用最新數據集網格,可以有效地解決數據流的概念轉移問題,使得算法的查準率得到保證。
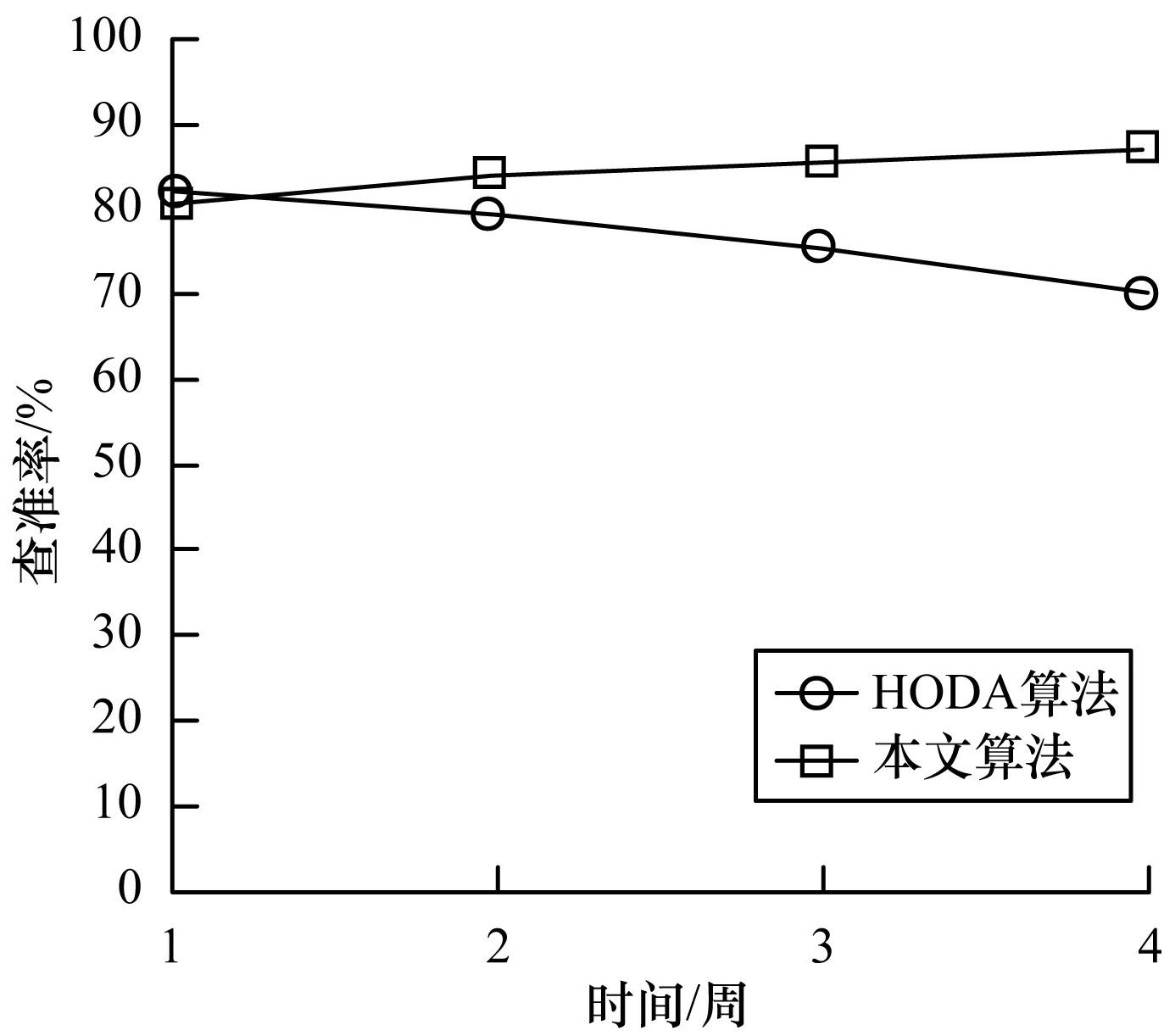
圖6 電梯異常數據查準率
5 結束語
本文基于角度分布的高維數據異常檢測方法,提出一種改進的異常檢測算法。在數據流檢測過程中,對數據集進行重要網格劃分和維護,降低角度方差計算代價,并且通過最近數據集的設定解決數據流中的概念轉移問題。實驗結果表明,該算法能有效識別高維數據流中的異常點,相比HODA算法,時間復雜度更低,適合于高維數據流的異常檢測。如何根據數據流的特點對閾值自適應,是下一步研究的內容。
[1] 曹東磊,曹建農,金蓓弘.一種無線傳感網絡中事件區域檢測的容錯算法[J].計算機學報,2007,30(10):1770-1776.
[2] DING J,WANG L,SHEN D,et al.An Anomaly Detection System on Big Data[J].Natural Science Journal of Hainan Universdity,2015(1):121-127.
[3] 費 歡,李光輝.基于K-means聚類的WSN異常數據檢測算法[J].計算機工程,2015,41(7):124-128.
[4] 凌 駿,尹博學,李 晟,等.基于監控數據的MySQL異常檢測算法[J].計算機工程,2015,41(11):41-46.
[5] 周曉云,孫志揮,張柏禮,等.高維類別屬性數據流離群點快速檢測算法[J].軟件學報,2007,18(4):933-942.
[6] KRIEGEL H P,VHUBERT M,ZIMEK A.Angle-based Outlier Detection in High Dimensional Data[C]//Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York,USA:ACM Press,2008:444-452.
[7] PHAM N,PAGH R.A Near-linear Time Approximation for Angle-based Outlier Detection in High Dimensional Data[C]//Proceeding of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York,USA:ACM Press,2012:877-885.
[8] 陳圣楠,錢紅燕,李 偉.基于角度方差的多層次高維數據異常檢測算法[J].計算機應用研究,2016,33(11):3383-3386.
[9] ZHANG Y,HAMM N,MERATNIA N.Statistics-based Outlier Detection for Wireless Sensor Networks[J].International Journal of Geo graphical Information Science,2012,26(8):1373-1392.
[10] 樸昌浩,黃 至,蘇 嶺,等.基于角度分布的高維數據流異常點檢測算法[J].上海交通大學學報,2014,48(5):647-652.
[11] KRIEGEL H P,HUBERT M S,ZIMEK A.Angle-based Outlier Detection Inhigh-dimensional Data[C]//Proceedings of IEEE KDD’08.Washington D.C.,USA:IEEE Press,2008:444-452.
[12] 劉 靖.復雜數據類型的離群檢測方法研究[D].廣州:華南理工大學,2014.
[13] SIMUNDIC A.Quality Indicators[J].Biochemia Medica,2008,18(3):311-319.
[14] FELDMAN D,SCHIDT M,SOHLER C.Turning Big Data Into Tiny Data:Constant-sizecoresets for K-means,PCA and Projective Clustering[C]//Proceedings of the 24th Annual ACM-SIAM Symposium on Discrete Algorithms.Washington D.C.,USA:IEEE Press,2013:1434-1453.
[15] 陳冠華,馬秀莉,楊冬青,等.面向高維數據的低冗余Top-k異常點發現方法[J].計算機研究與發展,2010,47(5):788-795.

