基于特別的特征表示方法的局部線性KNN算法*

卞則康，王士同，王宇翔

1.江南大學數字媒體學院，江蘇無錫 214122

2.中國船舶科學研究中心，江蘇無錫 214082

1 引言

近年來，圖像特征提取和圖像分類一直是人臉識別中的研究熱點，特征表示方法的選取直接影響到人臉圖像分類的效果。為了解決這些問題，提出了一些廣泛使用的特征提取算法，其中包括線性算法[1-3]和非線性算法[4-5]。此外，文獻[6]提出的基于稀疏表示的算法已經成功應用到人臉識別中，它解決了特征表示和分類之間的魯棒性問題。該算法通過學習得到測試樣本的稀疏表示，并將之應用到最小誤差分類器中進行分類。對于圖像分類，提出了多種特征提取的算法[7-9]，這些算法通過利用標簽信息來進行判別字典的學習和稀疏表示。但是這些方法也導致了其他問題，如分類的限制和計算的復雜性。

針對上述問題，本文提出了一種新的局部線性K最近鄰算法（locally linearKnearest neighbor method），即L2KNN算法。L2KNN算法首先提出了一種特別的特征表示方法，即應用重建、局部性和稀疏性的標準來表示每個測試數據。這種新的數據表示方法具有最近鄰集群效應（clustering effect of nearest neighbors，CENN），它能夠增強與測試樣本相同類別的訓練樣本的系數，增加相同類中訓練樣本的相關性。然后將學習得到的特征表示應用到圖像分類中，提出了一種新的分類器L2KNNc(L2KNN-based classifier）。

2 相關研究

基于局部特征稀疏編碼和基于全局特征編碼的特征表示方法是最常見的兩種特征表示方法，已經廣泛應用到目標識別[6]、場景識別[9]和動作識別[10-11]中。文獻[12]提出了一種使用稀疏編碼來學習字典和系數向量，從而表示圖像的局部特征的編碼學習算法。文獻[10]提出了一種帶局部約束的線性編碼方法，這種方法考慮到在特征編碼過程中的局部信息的約束。文獻[13]進一步提出了一種Laplacian系數編碼的特征表示方法，這種方法充分考慮到局部特征之間的相似性和局部性。

文獻[6]提出了一種基于全局特征的稀疏編碼方法，提高了人臉識別的魯棒性，并且進一步應用到其他的識別應用中，如目標識別、場景識別和動作識別。為了進一步提高算法的性能，提出了一些改進方法，如文獻[11]和文獻[14]在算法中考慮了字典的內相變化。另一種改進方法是通過對稀疏表示進行學習得到一個判別字典。文獻[7]提出了一種判別奇異值分解方法（discriminative singular value decomposition，D-KSVD），文獻[8]通過引進一個新的標簽一致的正則化項對文獻[7]中的方法進行改進。文獻[15]提出了一種聯合字典的學習方法（joint dictionary learning，JDL），通過對全局共享的字典和每個類特有的子字典進行學習得到聯合字典。文獻[9]提出了使用Fisher識別字典學習方法（Fisher discrimination dictionary learning，FDDL）來學習得到一個結構化字典，這個結構化字典中包含了一系列特定類的子字典。

相比之下，本文提出的L2KNN算法與上述使用判別字典的算法有以下不同：第一，L2KNN算法中不包含任何的判別項，主要著眼于建立特征表示的方法和其分類器之間的聯系，基于判別字典的方法沒有這種聯系。第二，本文算法不需要學習字典，避免了由于更新字典和稀疏系數帶來的時間消耗。第三，有些基于判別字典的算法需要對每一個類的子字典進行學習，如果每一個類的訓練樣本量較低，會影響算法的性能，而本文算法不需要對子字典進行學習。第四，有些基于判別字典的算法在其目標函數中包含線性分類器，這就排除了其他性能較好的非線性分類器，本文算法通過建立新的分類器來改善算法的分類性能，并且提高分類器的泛化性能。

3 算法描述

3.1 L2KNN算法

L2KNN算法首先提出了一種特別的特征表示方法，它表示一個測試樣本是所有訓練樣本的線性組合，如果測試樣本和訓練樣本屬于同一個類，則其相應的系數約束為非零，否則為零。具體方法如下：

假設給定m個訓練樣本bi∈Rn(i=1,2,…,m)，對于一個測試樣本x∈Rn，訓練樣本和測試樣本均用?2范式進行歸一化，相關系數向量v=[v1,v2,…,vm]T∈Rm,則測試樣本可以定義為：

其中，vi的定義如下：

上述特別的表示方法是一種高度的稀疏表示方法，即傳統的基于稀疏表示的方法[6]。傳統的基于稀疏表示的方法具有以下優點：第一，通過稀疏表示的方法構建的模型較直觀，容易被理解和操作。第二，基于稀疏表示的方法對目標圖像的識別是通過圖像的整體方面來把握的，通過對所有的訓練樣本進行訓練，得到一個相關系數，并依據相關系數進行分類識別。第三，在高維空間中，基于稀疏表示的特征表示方法受到特征提取的個數的限制較小，對圖像的識別率較高。

基于上述特別的特征表示方法的算法與傳統的基于稀疏表示的算法有以下不同：

（1）與測試樣本同類的訓練樣本之間往往是高度相關的，傳統的稀疏表示的方法傾向于求出其中一個訓練樣本非零系數[16]，而特別的特征表示方法是求出一組訓練樣本的非零系數。

（2）基于特別的特征表示算法具有最近鄰集群效應，加強了同類數據間的相關性。

（3）基于特別的特征表示算法的分類器的泛化性能較高。

為了解決上述的問題，在文獻[17]的啟發下，本文提出了L2KNN算法，算法的目標函數定義如下：

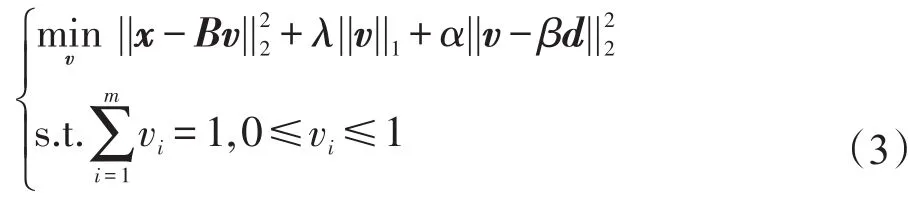
其中，x∈Rn表示測試樣本中的一個測試樣本；B=[b1,b2,…,bm]∈Rn×m表示所有的訓練樣本；v∈Rm是基于上述特別的特征表示方法下的相關系數向量。向量d=[d1,d2,…,dm]T∈Rm表示測試樣本和每一個訓練樣本之間的距離度量，具體的定義公式如下：

式（3）第一部分定義了重構標準，第二部分通過使用l1范數的魯棒性定義了稀疏標準，第三部分維持相關系數和距離度量之間的局部屬性。3個參數λ、α和β調節不同部分的比重。

本文提出的L2KNN算法顯示了最鄰近分組效應CENN，具體定義和證明如下：從CENN中可以看出，如果訓練樣本與測試樣本高度相關并且接近，則訓練樣本會獲得相似和大的相關系數，因此這些訓練樣本很有可能與測試樣本屬于同一類。L2KNN算法傾向于用相似且較大的相關系數來表示與測試樣本屬于同一類的訓練樣本，這與上文提出的特別的特征表示方法的情況一致。

定義1最近鄰集群效應CENN[17]：假設v=[v1,v2,…,vm]T是目標函數（3）的最優解，令ρ=biTbj(i,j=1,2,…,m)表示樣本bi和bj之間的相關系數。如果vi和vj的符號一致，則CENN可以表示為：

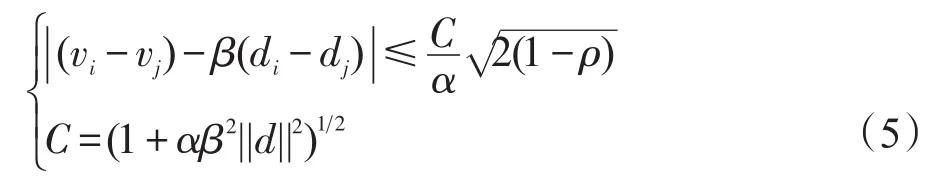
因為所有的實驗樣本都是經過?2范式進行歸一化，C是一個常數。

證明首先，式（3）等價于：

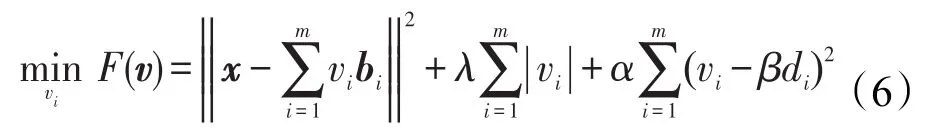
v=[v1,v2,…,vm]T是符合特別的特征表示的相關系數向量，因此分別對vi和vj求偏導，得出如下公式：

因為vi和vj的符號一致，所以sign(vi)=sign(vj)，將式（7）中兩個公式相減得：

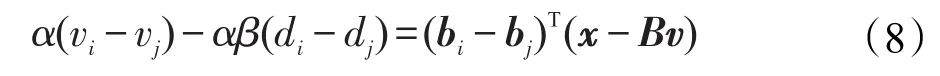
對式（8）兩邊取絕對值，并且F(v)≤F(0),‖x‖2=1,得：

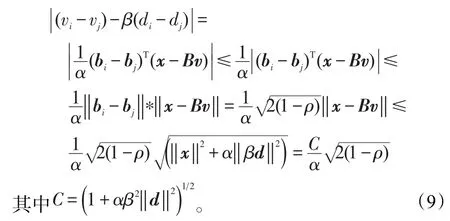
最近鄰集群效應CENN表明，如果兩個訓練樣本之間有一個很高的相關性，即ρ≈1，并且與測試樣本很接近（di≈dj，并且di、dj的數值也很大），則這兩個樣本的相關系數也相似，即vi≈vj。這正符合本文提出的特征表示方法的思想。

因此，本文提出的L2KNN算法不僅具有其他稀疏表示的優點，并且還具有最近鄰集群效應，對后續的分類步驟有很大的幫助。

3.2 算法求解

對于求解L2KNN算法，主要是優化公式（3），求解式（3）的過程實質上是一個正則化優化的過程，對于大多數的正則化求解，一般采用的是快速迭代閾值下降法（fast iterative shrinkage thresholding algorithm，ISTA）[18]。從式（3）的形式上看，其正則化包含了兩部分：一個?1正則化問題和一個?2正則化問題。第一部分體現了稀疏性，如同LASSO算法（least absolute shrinkage and selection operator）[19]；第二部分體現了系數之間的相關性。因此，式（3）可以使得相關性較高的特征集中在一起。借鑒文獻[17]的求解方法，對式（3）的變換如下表示：

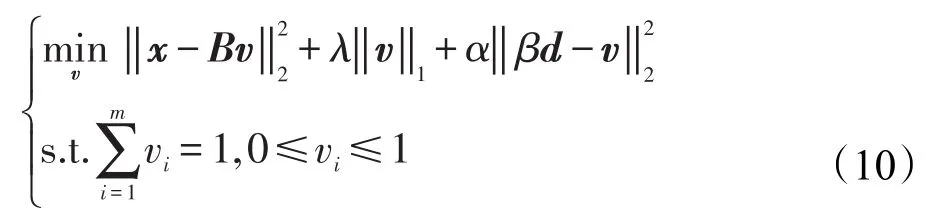
利用?2范式的性質，式（10）可以變化為：

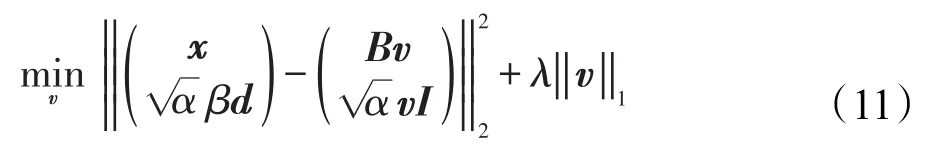
進一步轉化為：

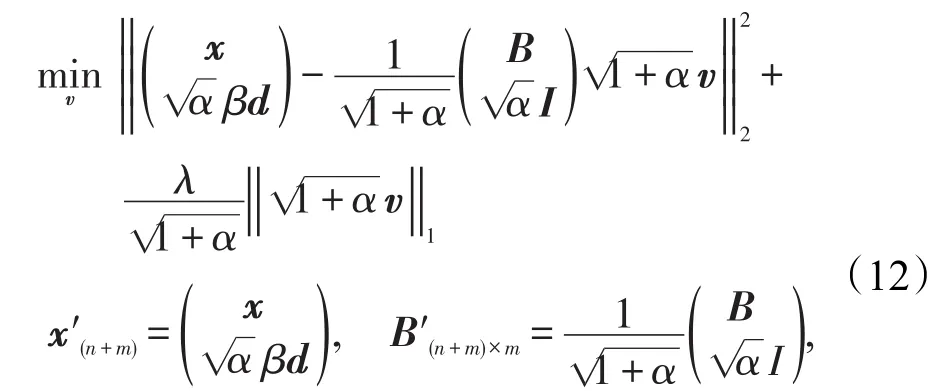
令：

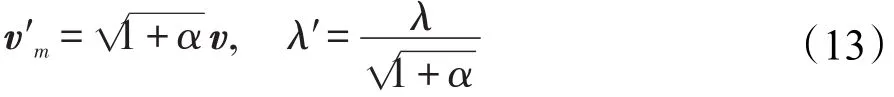
則目標函數轉化為帶?1正則化的LASSO型的目標函數：

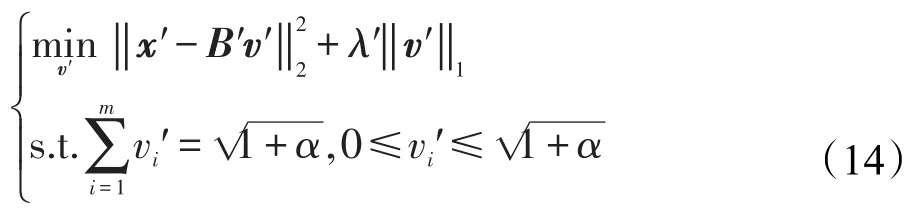
經過一系列的變換，將式（10）優化問題轉化成式（14）的優化問題。對于式（14）的優化求解，本文采用的是FISTA算法，具體的算法步驟詳見文獻[18]。

解決帶?1正則化的LASSO型目標函數可以表示為：

對于式（15）的求解，采用FISTA算法，其主要步驟如下：

算法1FISTA算法

輸入：Lf=2×λmax(ATA),λ,其中λmax()表示最大特征值

初始化：y1=x0∈Rn,t1=1

Stepk(k＞0)：計算

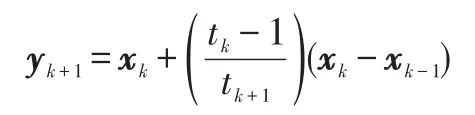
直至滿足停止條件

輸出：x

應用FISTA算法的求解LASSO算法，提高了算法的運算速率，時間復雜度為O(1/k2)。

因此L2KNN算法的求解步驟如下：

算法2L2KNN算法

輸入：訓練數據集B∈Rn×m，測試數據集X∈Rn×N

實驗參數：λ、α、β、δ

1.使用式（4）計算出d。

2.根據式（13）構造出新的B′、x′、λ′。

3.應用算法1中的FISTA算法求解式（14）。

輸出相關系數矩陣：V∈Rm×N

3.3 L2KNNc分類器

通過上述所示的算法求出相關系數向量v，對于測試樣本x進行分類，使用如下的分類器：

其中，c表示樣本中的總類別數；Bc表示第c類的訓練樣本集合。L2KNNc分類器對測試數據進行分類，是計算每一個類別中的訓練樣本的相關系數的和，通過比較每個類別相關系數和的大小決定測試數據屬于哪一個類別。如圖1所示。

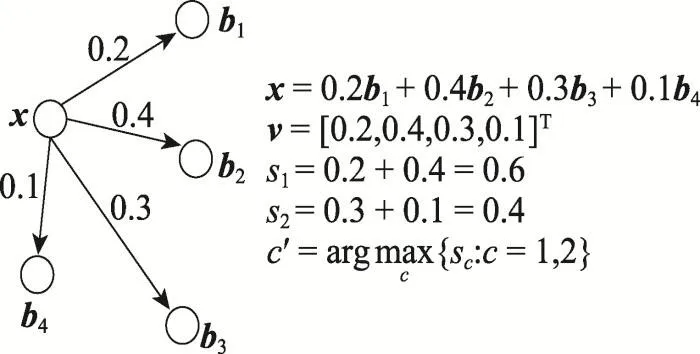
Fig.1 L2KNNcclassifier圖1 L2KNNc分類器

圖1顯示有4個訓練樣本b1、b2、b3、b4，它們的標簽分別是1、1、2、2。訓練樣本對于測試樣本x的系數向量為v=[0.2,0.4,0.3,0.1]T，分類器通過比較s1＞s2，判定測試樣本x屬于1類。

但是值得注意的是，當有的訓練樣本中混入了一些噪聲，使得同一類中一些訓練樣本遠離測試樣本，這樣它的系數就成為拖尾系數，由式（16）定義的L2KNNc分類器的泛化性能會有所下降。在實際應用中，同一類中不是所有的訓練樣本都需要，一些受到噪聲影響的樣本所帶有的拖尾系數反而降低了分類性能。因此，為了提高L2KNNc分類器的泛化性能，使用系數截斷以提高算法的性能，在分類過程中只需要每一類中前k個最大的vi系數，用前k個系數的和作為判斷依據，具體如下：

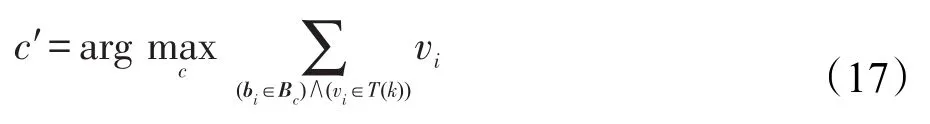
這里，T(k)表示每一類中前k個最大的系數集合。在實際應用中，參數k的設置對算法的分類性能有重要的影響。

3.4 時間復雜度分析

本文提出的L2KNN算法的時間消耗主要集中在算法2中第1、第3步。對于每一個n維的測試樣本，第1步需要分別計算出與m個訓練樣本的距離度量，則算法2中第1步的時間復雜度為O(mn)。在應用FISTA算法求解過程中，FISTA算法收斂的時間復雜度為O(1/k2)，k表示迭代的總次數，在每次迭代中，求解梯度的時間復雜度為O(mn)，則算法2中第3步的時間復雜度為O(mn/k2)。則運行一次L2KNN算法的時間復雜度為O((mn/k2)+mn)。

4 實驗

4.1 實驗數據和實驗設置

為了測試本文算法的分類性能，在人臉數據集上進行實驗，一共4個人臉數據集，分別是AR Face[20]、Extended Yale Face B[21]、ORL Face[22]和 PIE[23]。為了檢測本文算法的分類性能，一共選取了3種對比算法，分別是SRC、FDDL[9]、LASSO[19]算法。分別比較本文算法與3種對比算法在不同數據集上的分類準確率和標準差。

本文提出的L2KNN算法存在4個參數λ、α、β和δ。因為數據集的不同，所以每個數據集的參數的取值也不一樣。因此對于每一個數據集，本文需要進行尋參操作，選取最佳的實驗參數。其中參數α、λ、δ的取值范圍可以表示為{0.001,0.005,0.010,0.020,0.050,0.100},β為{1,2,3,4,5,6}。通過對前一個集合中隨機抽取3個數（可重復抽取）組合作為參數α、λ、δ的值，可以組成36組，再從第二個集合中抽取一個數作為β的值，則一共有36×6組的參數組合。對于每一個數據集，需要用本文算法對這36×6組的參數組合進行實驗，通過實驗結果選取正確率最高的參數組合，這個過程便是本文的尋參操作。通過尋參操作確定的參數組合將是后續對比實驗中本文算法的參數值。

本文的實驗評價標準選擇算法的分類準確率和標準差，其中分類標準差表明算法的穩定性。為了比較算法的運行速率，本文實驗選擇的比較標準是單個樣本的運行時間，即算法運行一次的總時間除以測試樣本的總數，這是一個平均時間。

為了檢測算法的最近鄰集群效應，本文借鑒文獻[17]中的兩種評價方法，即正確激活率（true accept rate，TAR）和假激活率（false accept rate，FAR），具體定義如下：

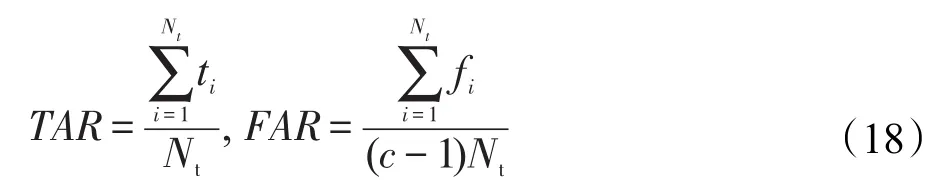
其中，Nt表示測試樣本的數量；c表示樣本的類別總量；ti表示第i個測試樣本中非零相關系數所對應的訓練樣本中與第i個測試樣本屬于同一類的訓練樣本個數；fi表示與第i個測試樣本同屬一類的訓練樣本中相關系數為0的樣本的個數。

4.2 實驗結果與分析

4.2.1 Extended Yale Face B數據集

本小節實驗選取的是Extended Yale Face B數據集，本文使用的是一種常用的裁剪版本[25]，所有的圖像經過手動對齊、裁剪，然后調整大小為168×192像素。本次實驗的訓練數據和測試數據的選取規則如下：每次實驗，對于每一類，隨機選取其中的20幅圖像作為訓練集，余下的圖像作為測試集。圖像數據在使用之前要使用PCA（principal component analysis）降維方法將圖像數據的維度降至300維。經過參數尋優后，本次實驗中L2KNN算法的實驗參數設置如下：δ=0.1,λ=0.01,α=0.005,β=5，設置L2KNNc分類器的參數k=6。實驗一共運行10次，實驗結果取平均值，如表1所示。

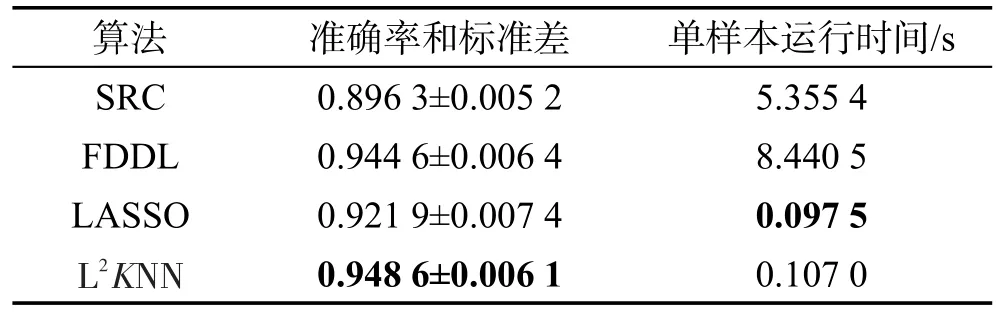
Table 1 Results of experiment onYale Bdatabase表1 Yale B數據集實驗結果

表1是各算法的實驗準確率和標準差。實驗數據表明，本文提出的L2KNN算法相比其他3種經典的算法具有很好的分類性能。相比兩種經典的基于字典學習判別的算法，本文算法具有較好的準確率，相比FDDL算法具有一定的穩定性，相比SRC算法準確率較高。本文算法在計算過程中避免了更新字典所帶來的時間消耗，因此本文算法在運行時間消耗上小于這兩種算法。相比傳統的LASSO算法，L2KNN算法加入了最近鄰集群項，提高了算法的分類性能，并使用系數截取的方式增強了分類器的泛化性能，提高了算法的分類性能和穩定性。

4.2.2 AR Face數據集

本次實驗選用的數據集是人臉識別中常用的AR Face數據集，此數據集一共包含126個人臉的圖像。本文選用其中一種常用的數據子集，50名男性和50名女性的圖像構成一個新的數據集，這些圖像被統一縮放到165×120像素，此數據集是本次的實驗數據集。對于本次實驗的訓練集和測試集的構造方法如下：對于每一類的圖像，AR數據集隨機抽取10張作為訓練數據集，余下的作為測試數據集。數據在使用之前將圖像向量的維度用PCA降維到200維。經過參數尋優后，L2KNN算法的實驗參數設置如下：δ=0.01,λ=0.01,α=0.01,β=5。設置L2KNNc分類器的參數k=5。實驗一共運行10次，實驗結果取平均值，如表2所示。

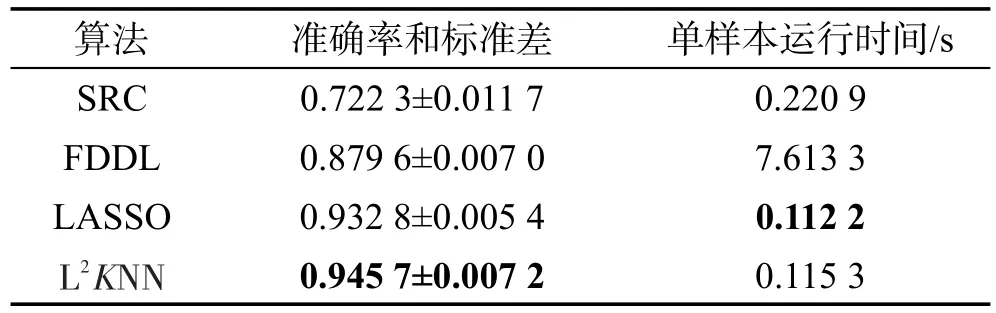
Table 2 Results of experiment onAR database表2 AR數據集實驗結果

表2的實驗結果表明，本文提出的L2KNN算法的運行效率比常用的基于字典判別的算法SRC、FDDL的運行效率高，相比于經典的LASSO算法，本文算法的運行效率大致相當。在算法的分類準確率方面，L2KNN算法具有比其他3種算法高的分類性能。相比于4.2.1小節中的實驗設置，對每一類訓練樣本選取的數量減少，因此基于字典判別的算法的分類準確率下降較快。本文算法直接建立特征表示與分類器之間的聯系，因此分類性能基本上沒受影響，并且分類性能和穩定性比SRC、FDDL算法好。L2KNN算法相比LASSO算法，增加了最近鄰集群的性能，在訓練樣本減少的情況下，分類性能沒受太大的影響。

4.2.3 ORL Face數據集和PIE數據集

為了進一步研究算法的分類性能。本次實驗選擇ORL Face數據集和PIE數據集。ORL數據集含有40個不同的目標，每個目標含有10張圖像，是一個較小的數據集。PIE數據集是一個較大的人臉數據庫，本文選用其中的一個子集作為本次實驗的數據集，即共有68個不同的人臉數據，每個人選取170張圖像。對于ORL數據集先縮放至64×64像素，再使用PCA降維至100維；對于PIE數據集縮放至32×32像素，再使用PCA降維至200維。每個數據集運行10次，實驗結果取均值。

對于數據集ORL，每一類中隨機選取3張圖像作為訓練集，余下的7張作為測試集。實驗的參數設置為：δ=0.01,λ=0.01,α=0.005,β=5。對于L2KNNc分類器設置k=2。實驗結果如表3所示。

Table 3 Results of experiment onORLdatabase表3 ORL數據集實驗結果

對于數據集PIE，每一類中隨機選取15張圖像作為訓練集，余下的155張作為測試集。實驗的參數設置為：δ=0.01,λ=0.02,α=0.01,β=6。對于L2KNNc分類器設置k=10。實驗結果如表4所示。

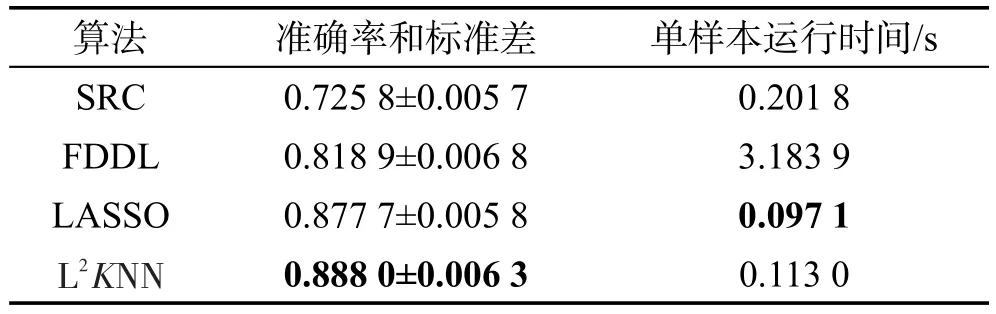
Table 4 Results of experiment onPIEdatabase表4 PIE數據集實驗結果

表3和表4的實驗結果顯示，在較小數據集中，因為訓練樣本較少，所以算法的分類性能都出現了一定程度的下降。在較大的數據集中，由于在每一類中選取的訓練樣本相對樣本的總量較少，不能有效地學習出有用信息，從而影響到算法的分類性能。實驗結果表明，在較大的和較小的數據集中，本文提出的L2KNN算法具有較好的分類性能，運行時間較少，算法的性能比較穩定。

4.2.4 最近鄰集群效應的有效性和算法的泛化性能

最近鄰集群效應是本文提出的L2KNN算法的重要理論依據。為了評估CENN對于L2KNN算法的影響，通過設置不同的實驗參數λ、α、β，比較分類準確率、正確激活率（TAR）和假激活率（FAR）的數值變化。TAR和FAR的具體含義，以Extended Yale Face B數據集為例，其中一個類a的訓練樣本個數是20個，如果測試樣本與訓練樣本同屬于a類，則TAR的最理想值為20，即a的訓練樣本的數量，則FAR的理想值為0。實驗結果如表5所示。

Table 5 Results of experiment on Yale B database表5 Yale B數據集的實驗指標

表5的實驗結果表明，在相同的λ、β下，隨著α的增大，算法的分類準確率在增加，算法的TAR值在增加，FAR值在減小。這意味著，算法的集群效應在增加，算法的分類性能在提高，對于樣本而言，正確激活的數量在增多，錯誤激活的數量在減少。同樣的，在相同的λ、α下，隨著β的增加，也會出現相同的效果。從表5的實驗結果中還可以看出，當α、β一定的情況下，隨著λ的增加，抑制了集群效應，使得算法的準確率在下降，TAR在下降，FAR在上升。

為了提高本文算法的泛化性能，本文使用系數截斷的方法，選取系數前k個最大的系數作為分類器的分類標準。為了測試k值對于L2KNNc分類的影響，本次實驗選取Extended Yale Face B數據集，實驗數據的設置如4.2.1小節，對于AR Face數據集，實驗參數的設置如4.2.2小節。實驗結果如圖2和圖3所示。

從圖2和圖3的實驗結果中可以看出，k值的改變能夠影響算法的分類效果。隨著k值的增加，算法的分類準確率也在增加，但是到達一個最大值之后，隨著k值的增加，算法的性能不會增加，甚至出現降低。因此，系數截斷的方法可以丟棄一些“較遠”的數據影響，有效地增加算法分類性能，提高算法的泛化性能。圖2和圖3的實驗結果證明，選擇一個合適的k值對算法的分類性能具有重要的影響。

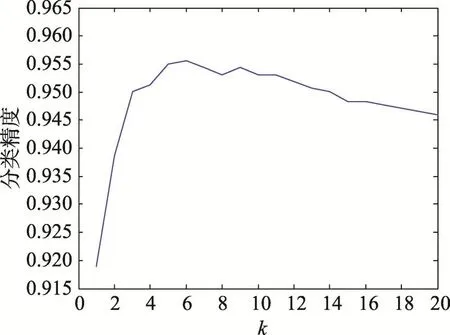
Fig.2 Accuracy ofL2KNNcbased on Yale Bdatabase for differentk圖2 對不同k取值L2KNNc分類器在Yale B數據集上的準確率

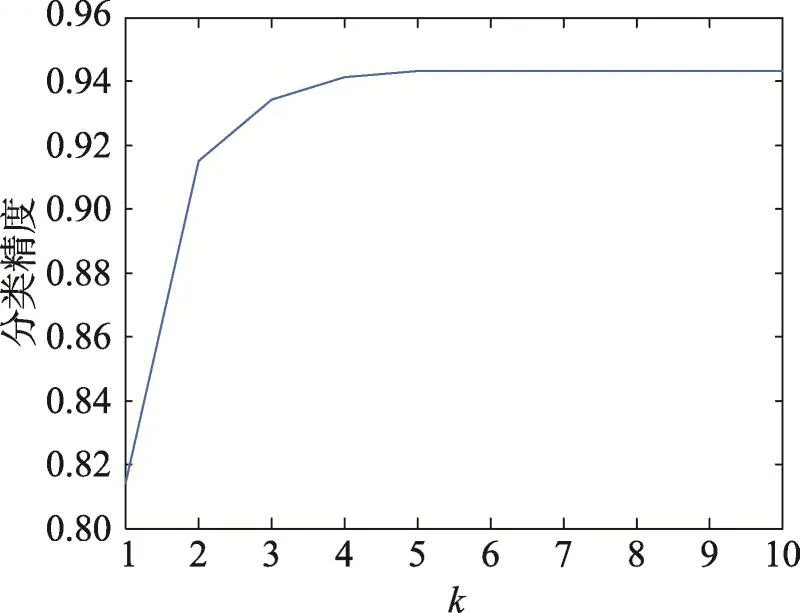
Fig.3 Accuracy ofL2KNNcbased on ARdatabase for differentk圖3 對不同k取值L2KNNc分類器在AR數據集上的準確率

5 結束語

本文提出了一種基于特別的特征表示方法的局部線性KNN分類算法(L2KNN算法)，并將之應用到人臉識別中。在L2KNN算法中提出了一種特別的特征表示方法，其具有最近鄰集群效應，增加了同類數據之間的相關性。使用系數截斷的方法增加了分類器L2KNNc的泛化性能，進一步提升了算法的分類性能。本文使用FISTA算法優化目標函數，提高了算法的運行速率。實驗結果表明，本文提出的L2KNN算法的實用性和有效性較佳。

[1]Turk M,Pentland A.Eigenfaces for recognition[J].Journal of Cognitive Neuroscience,1991,3(1):71-86.

[2]Belhumeur P N,Hespanha J P,Kriegman D J.Eigenfaces vs fisherfaces:recognition using class specific linear projection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1997,19(7):711-720.

[3]Liu Chengjun,Yang Jian.ICA color space for pattern recognition[J].IEEE Transactions on Neural Networks,2009,20(2):248-257.

[4]Liu Chengjun.Capitalize on dimensionality increasing techniques for improving face recognition grand challenge performance[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2006,28(5):725-737.

[5]You Di,Hamsici O C,Martinez A M.Kernel optimization in discriminant analysis[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,33(3):631-638.

[6]Wright J,Yang A Y,Ganesh A,et al.Robust face recognition via sparse representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2008,31(2):210-227.

[7]Zhang Qiang,Li Baoxin.DiscriminativeK-SVDfor dictionary learning in face recognition[C]//Proceedings of the 23rd Conference on Computer Vision and Pattern Recognition,San Francisco,Jun 13-18,2010.Washington:IEEE Computer Society,2010:2691-2698.

[8]Jiang Zhuolin,Lin Zhe,Davis L S.Label consistentK-SVD:learning a discriminative dictionary for recognition[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(11):2651-2664.

[9]Yang Meng,Zhang Lei,Feng Xiangchu,et al.Sparse representation based Fisher discrimination dictionary learning for image classification[J].International Journal of Computer Vision,2014,109(3):209-232.

[10]Chen Junzhou,Li Qing,Peng Qiang,et al.CSIFT based locality-constrained linear coding for image classification[J].PatternAnalysis andApplications,2015,18(2):441-450.

[11]Zhao Zhongqiu,Cheung Y M,Hu Haibo,et al.Expanding dictionary for robust face recognition:pixel is not necessary while sparsity is[J].IET Computer Vision,2015,9(5):648-654.

[12]Shi Jun,Li Yi,Zhu Jie,et al.Joint sparse coding based spatial pyramid matching for classification of color medical image[J].Computerized Medical Imaging and Graphics,2014,41(1):61-66.

[13]Gao Shenghua,Tsang W H,Chia L T.Laplacian sparse coding,hypergraph Laplacian sparse coding,and applications[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(1):92-104.

[14]Deng Weihong,Hu Jiani,Guo Jun.Extended SRC:undersampled face recognition via intraclass variant dictionary[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2012,34(9):1864-1870.

[15]Feng Zhizhao,Yang Meng,Zhang Lei,et al.Joint discriminative dimensionality reduction and dictionary learning for face recognition[J].Pattern Recognition,2013,46(8):2134-2143.

[16]Zou Hui,Hastie T.Regularization and variable selection via the elastic net[J].Journal of the Royal Statistical Society:Series B Statistical Methodology,2005,67(5):301-320.

[17]Liu Qingfeng,Liu Chengjun.A novel locally linearKNN method with applications to visual recognition[J].IEEE Transactions on Neural Networks and Learning Systems,2017,28(9):2010-2021.

[18]Beck A,Teboulle M.A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J].SIAM Journal on Imaging Sciences,2009,2(1):183-202.

[19]Tibshirani R.Regression shrinkage and selection via the LASSO[J].Journal of the Royal Statistical Society:Series B Methodological,1996,58(1):267-288.

[20]Martinez A M,Kak A C.PCA versus LDA[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2001,23(2):228-233.

[21]Lee K C,Ho J,Kriegman D J.Acquiring linear subspaces for face recognition under variable lighting[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(5):684-698.

[22]Ahonen T,Hadid A,Pietik?inen M.Face recognition with local binary patterns[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2006,28(12):2037-2041.

[23]Sim T,Baker S,Bsat M.The CMU pose,illumination,and expression database[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2003,25(12):1615-1618.