糾刪碼存儲系統單磁盤錯誤重構優化方法綜述

傅穎勛 文士林 馬 禮 舒繼武

1(北方工業大學計算機學院 北京 100144)

2(清華大學計算機科學與技術系 北京 100084)

(mooncape1986@126.com)

隨著云計算的迅猛發展，許多依托互聯網的大數據應用開始涌現，數據量呈爆炸式地增長.已有調查報告顯示，2015年全球服務器共產生了8.61 ZB的大數據，在此后的10年里，存儲服務器的總量還將增長10倍[1].由于磁盤是當前云存儲/數據中心中的主要存儲介質，而它每年發生錯誤的概率在1.7%～13%之間[2]，這意味著每年都有大量的磁盤發生錯誤.因此，現有存儲系統需要在磁盤錯誤的情況下保障數據的可靠性，并繼續提供存儲服務.

目前，用于提升存儲系統數據可靠性的技術主要有多副本技術和可靠性編碼技術2種，其中多副本技術具有數據高可用性的特點，通常被用于數據訪問密集型的存儲系統中[3].可靠性編碼技術包括網絡編碼和糾刪碼兩大類.其中，網絡編碼主要應用于數據通信領域，直到近幾年才開始被引入存儲系統[4]；糾刪碼則是存儲系統中常用的可靠性編碼技術.

隨著存儲系統的興起，數據逐漸變得比存儲介質更加重要，糾刪碼因高存儲利用率、低存儲開銷等特點，被廣泛應用于各種存儲系統中.到了大數據時代，一方面，由于多副本機制要占用大量的存儲空間，已逐漸不適應數據中心等大規模存儲系統的需求，越來越多的存儲系統開始采用糾刪碼技術，以保障數據的可靠性[5-7]；另一方面，存儲系統中磁盤錯誤的問題也越來越突出.當磁盤發生不可修復的錯誤后，存儲系統需要利用其它磁盤中的冗余信息重構所有失效數據.在有一定規模的云存儲/數據中心中，每天都有大量的磁盤發生錯誤，因此，如何快速重構錯誤磁盤中的失效數據，已成為當前存儲系統中的核心問題之一.學術界和工業界對此非常重視，也產生了大量的研究成果，例如用于優化現有糾刪碼重構效率的RDOR方法[8]、SIOR方法[9]以及專門用于提升重構效率的LRC碼[10]、zigzag碼[11]等.由于單磁盤錯誤在所有磁盤錯誤中占據了99.75%以上的比例[12]，現有的研究主要針對單磁盤錯誤下的數據重構效率進行優化.

本文從目前存儲系統對糾刪碼技術的需求出發，首先介紹了糾刪碼的一些重要術語與定義[13]，接著介紹了單磁盤錯誤重構技術的混合優化原理，并詳細闡述了近幾年關于單磁盤錯誤重構優化的研究成果，最后指出了未來的研究方向.

1 糾刪碼概述

1.1 重要術語與定義

1) 數據(data).由原始用戶產生的一系列信息，通常以文件的形式存放在計算機系統中.

2) 冗余(redundant).為了提高計算機系統的可靠性，人們在存儲數據信息的同時，也會額外存放一些由數據信息計算而來的校驗信息，這些額外存放的信息則被稱為冗余信息.

3) 元素(element).一簇固定大小的存儲單元，用于存放數據內容或冗余信息.一般情況下，存放數據內容的元素被稱為數據元素，存放冗余信息的元素則被稱為校驗元素，例如：圖1中的d0,0是數據元素，p0,4是校驗元素.

Fig. 1 An example of one stripe圖1 條帶的例子

4) 失效元素(lost element).當系統中存在磁盤錯誤時，錯誤磁盤中的所有元素均為失效元素.

5) 條帶(stripe).在糾刪碼領域中，條帶是最小的邏輯單位，它由一系列數據元素和校驗元素組成，各條帶之間的編碼關系相互獨立，即：在1個條帶內，所有的校驗元素均由當前條帶中的數據/校驗元素計算而來，且條帶內的所有數據元素都不被用于計算其他條帶中的校驗元素.圖1給出了包含6磁盤的RDP碼的1個條帶.

6) 條塊(strip).條帶中的每1列被稱為1個條塊(圖1中的Di與Pi都是條塊)，當糾刪碼被應用到實際存儲系統中時，各條塊會被映射到不同的物理磁盤上.因此，存儲系統中的磁盤錯誤，邏輯上可以看成是條塊失效.

7) 存儲利用率(storage usage rate).數據信息占當前已使用存儲空間的比例.在糾刪碼中，存儲利用率等于存儲系統中的數據總量除以已使用的存儲空間總量.

8) 容錯能力(fault tolerance).能夠容忍的最大失效條塊數.若某糾刪碼在任意f個條塊同時失效的情況下，能夠還原所有數據信息，且至少存在一種f+1個條塊失效的情況，使得該糾刪碼無法還原所有數據信息，則稱該糾刪碼的容錯能力為f.

9) 條帶棧(stack).由于一些特殊的原因，存儲系統在將各條塊映射到物理磁盤時，通常會采用一些特殊的映射機制，條帶棧是用來表示由條塊映射到物理磁盤的完整機制.圖2給出了一種常見的條帶棧的例子.該條帶棧采用循環左移的映射方式，以減輕橫式編碼校驗盤讀寫負載過重的問題.

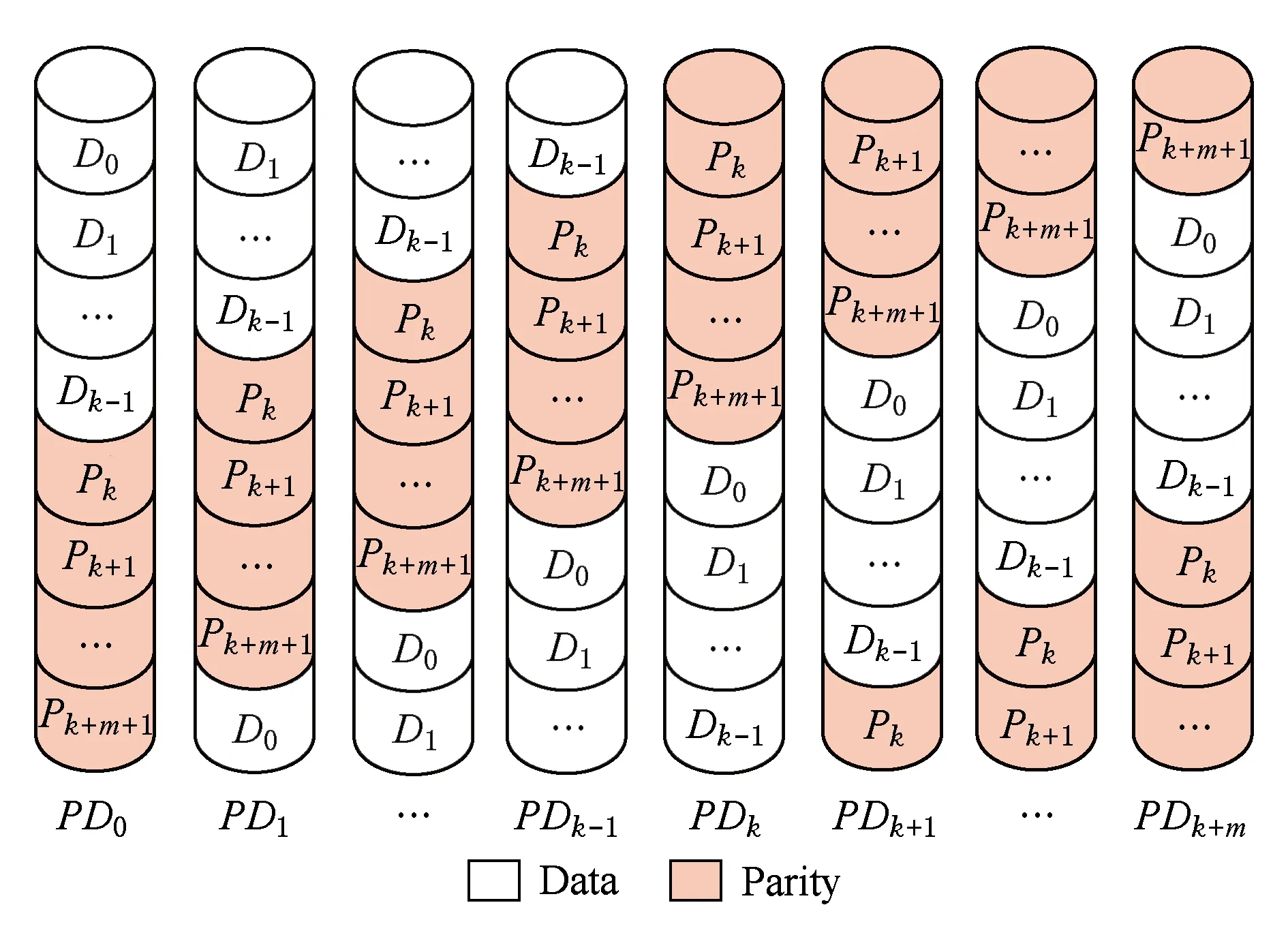
Fig. 2 An example of one typical stack圖2 典型條帶棧的例子

10) 磁盤錯誤(disk failure).磁盤因硬件故障等因素，導致數據失效的情況.

11) 單磁盤錯誤重構(single disk failure recovery).針對單個磁盤錯誤，利用剩余數據/冗余信息重構錯誤磁盤中的所有內容.

1.2 典型的糾刪碼

目前的主流糾刪碼可根據校驗元素的生成方式分為2類：基于伽羅華域(GF(2n))運算[14]的糾刪碼和基于異或運算的糾刪碼.基于伽羅華域運算的糾刪碼的主要特征在于，其編碼過程的所有運算都在伽羅華域中進行，包括RS (Reed-Solomon)碼[15]、LRC (local reconstruction codes)碼[10]、stair碼[16]、SD (sector-disk)碼[17]等.其中，RS碼是最早的糾刪碼，其容錯能力可以根據存儲系統的需要無限擴充，且具有MDS (maximum distance separable)屬性[13]，即擁有理論最優的存儲利用率；LRC碼是一種被廣泛應用在微軟等企業級云存儲的糾刪碼技術，可提升存儲系統降級讀性能；SD碼和stair碼是新型糾刪碼，它們不但考慮了磁盤錯誤，同時還針對磁盤的某些扇區錯誤進行了優化.

由于伽羅華域中的乘法運算具有很高的計算復雜度，因此，基于伽羅華域運算的糾刪碼的編/解碼效率相對較低.相比之下，由于基于異或運算的糾刪碼在編/解碼過程中僅使用“異或”運算，因此擁有很高的編/解碼效率.根據校驗元素的分布情況，基于“異或”運算的糾刪碼可分為橫式編碼和縱式編碼2類.其中，橫式編碼的典型特征是數據元素和校驗元素分別存放在不同的條塊內，包括RDP (row -diagonal parity)碼[18]、blaum-roth碼[19]、evenodd碼[20]、liberation碼[21]、liber8tion碼[22]、廣義RDP碼[23]、star碼[24]、柯西RS碼[25]等.其中，RDP碼、evenodd碼、liberation碼、liber8tion碼為RAID-6 (redundant array of independent disks)編碼，能容任意2個磁盤錯誤；star碼可以看成一種由evenodd碼派生而成的編碼，能容任意3個磁盤錯誤.廣義RDP碼的限制條件較多，但具有較好的容錯能力，在某些特定的條件下甚至能容8個磁盤錯誤.橫式編碼通常能夠構建于任意數量的磁盤之上，但是，它們通常無法獲得理論最優的編/解碼計算復雜度，以及理論最優的單數據元素更新復雜度.

縱式編碼通常將數據元素和校驗元素混合存放在相同條塊中，典型的有X碼[26]、HDP (horizontal- diagonal parity)碼[27]、H碼[28]、HV (horizontal-vertical)碼[29]、D碼[30]、hover碼[31]、weaver碼[32]等.其中，X碼、HDP碼、H碼、HV碼和D碼都是RAID-6編碼且擁有理論最優的存儲利用率，但它們的容錯能力相對較低，僅能容任意2個磁盤同時出錯；hover碼和weaver碼是高容錯編碼，可以達到較高的容錯能力，但存儲利用率較低.相比于橫式編碼，縱式編碼的編/解碼計算復雜度、單個數據元素的更新復雜度通常能夠達到理論最優，但難以構建于任意數量的磁盤之上[33].圖3給出了1個包含5磁盤的liberation碼的例子.

Fig. 3 5-disks Liberation code圖3 5-磁盤Liberation碼

1.3 糾刪碼的生成矩陣

在糾刪碼中，校驗元素可以用數據元素乘1個矩陣來表示，這個矩陣也被稱為糾刪碼的生成矩陣(generation matrix).在糾刪碼的編碼過程中，矩陣加法用“異或”運算代替，乘法用伽羅華域中的“乘運算”代替.特別地，當生成矩陣中的所有元素均為“0”或者“1”時，伽羅華域“乘運算”可以轉換為邏輯運算中的“與”操作，由此產生的生成矩陣也被稱為“點陣(bitmatrix)”，相應的糾刪碼就是上文曾提到的基于“異或”運算的編碼.一般來說，糾刪碼生成矩陣由上下2部分組成：上半部分是1個單位矩陣，下半部分則是編碼矩陣.根據矩陣乘法原理，糾刪碼中數據元素與生成矩陣相乘所得到的積，便是存放在系統中所有的數據元素與校驗元素.圖4給出了圖3所示的5磁盤liberation碼的生成矩陣.

Fig. 4 Generation matrix for erasure code圖4 糾刪碼的生成矩陣

2 混合重構思想

目前，單磁盤錯誤重構的優化主要基于混合重構思想.本節先介紹重構相關的等式，然后再給出混合重構思想的基本原理.

2.1 重構等式

在基于“異或”運算的糾刪碼中，由于生成矩陣每行中“1”所對應的數據元素與該行對應的校驗元素的異或和為0，因此可以用“等式”表示.這些等式又稱“原始等式”[34].例如圖3所示的5磁盤Liberation碼中共有6個原始等式：

d0,0⊕d0,1⊕d0,2⊕p0,3=0;

(1)

d1,0⊕d1,1⊕d1,2⊕p1,3=0;

(2)

d2,0⊕d2,1⊕d2,2⊕p2,3=0;

(3)

d0,0⊕d1,1⊕d2,2⊕p0,4=0;

(4)

d1,0⊕d1,1⊕d2,1⊕d0,2⊕p1,4=0;

(5)

d2,0⊕d0,1⊕d0,2⊕d1,2⊕p2,4=0.

(6)

出現磁盤錯誤時，糾刪碼的每個條帶都存在一定數量的失效數據元素/校驗元素，這些元素分別被包含在1個或多個原始等式中.若將原始等式中的某個元素移到等式的右邊，并將該元素用其他元素的“異或和”表示，隨后在其他原始等式中代入該元素，則會生成一些新的等式:

d0,0=d0,1⊕d0,2⊕p0,3，

(7)

將式(7)代入式(4)，得：

d0,1⊕d0,2⊕p0,3⊕d1,1⊕d2,2⊕p0,4=0.

(8)

所產生的等式可以再次迭代，例如可將式(8)中的d2,2用其他元素的異或和表示，并代入式(3)，從而形成新的等式.循環上述過程，將所有的元素都用所有潛在可能的方式表示(即對于每個等式中的每個元素，都用其他元素的異或和表示)，并代入到其他所有包含此元素的等式中(含新產生的等式)，直到不再產生新的等式為止(即所有新產生的等式都是之前出現過的).本文稱這些由迭代變換所產生的等式為二次等式，并定義Eall為所有原始等式“并”所有二次等式的集合，定義F為所有失效元素的集合，Ei,j為能夠直接計算出數據元素di,j或校驗元素pi,j的重構等式.顯然，對任意ei∈Eall，若ei∩F={di,j}或ei∩F={pi,j},則ei∈Ei,j.

重構等式是單磁盤錯誤重構的基礎，這些等式既可以由數學推導生成，也可以由計算機枚舉迭代獲得.例如在圖3的例子中，若D1發生錯誤，數據元素d0,1,d1,1,d2,1對應的重構等式為

d0,1⊕d0,0⊕d0,2⊕p0,3=0;

(9)

d0,1⊕d2,0⊕d0,2⊕d1,2⊕p2,4=0;

(10)

d1,1⊕d1,0⊕d1,2⊕p1,3=0;

(11)

d1,1⊕d0,0⊕d2,2⊕p0,4=0;

(12)

d1,1⊕d1,0⊕d2,0⊕d0,2⊕d2,2⊕p2,3⊕p1,4=0;

(13)

d2,1⊕d2,0⊕d2,2⊕p2,3=0;

(14)

d2,1⊕d0,2⊕d1,2⊕p1,3⊕p1,4=0;

(15)

d2,1⊕d0,0⊕d1,0⊕d0,2⊕d2,2⊕p0,4⊕p1,4=0.

(16)

2.2 優化原理

當基于異或運算的糾刪碼中出現單磁盤錯誤時，傳統的重構方法首先尋找1塊校驗磁盤(橫式編碼)或一種類型的全部校驗元素(縱式編碼)，然后用原始等式重構失效數據.特別地，若出錯的是校驗磁盤，則直接用所有的數據磁盤和原始等式重新計算校驗元素.例如在圖3所示的Liberation碼中，當磁盤1發生錯誤時，傳統方法將利用式(9)(11)(14)，分別按3條規則進行重構：

d0,1=d0,0⊕d0,2⊕p0,3;

(17)

d1,1=d1,0⊕d1,2⊕p1,3;

(18)

d2,1=d2,0⊕d2,2⊕p2,3.

(19)

這種方法需要在D0,D2,P3中各讀取3個元素，總共需要讀取9個元素，再經過6次異或運算，才能重構所有的失效元素.然而，若適當利用磁盤P4中的一些校驗元素，雖然異或運算的次數會增加，但需要讀取的元素在總量上可能會減少.針對這一特點，文獻[8]首次提出了一種基于RDP碼的混合重構算法——RDOR算法，巧妙地利用了第2塊校驗盤中的一些元素，以提升數據重構的性能.本文將在3.1節中詳細介紹RDOR算法，在此先以圖3中的5磁盤Liberation碼為例，介紹混合重構的基本原理.

在圖3所示編碼中，若D1發生錯誤，則用式(9)(11)(15)的重構過程為

d0,1=d0,0⊕d0,2⊕p0,3;

(20)

d1,1=d1,0⊕d1,2⊕p1,3;

(21)

d2,1=d0,2⊕d1,2⊕p1,3⊕p1,4.

(22)

顯然，這種方法只需讀取7個不同的元素；d0,2,d1,2,p1,3各參加了2次異或運算，總共運行了7次“異或”運算.由于磁盤I/O速度遠低于“異或”運算速度，因此混合重構方法能夠有效地提升單磁盤錯誤的重構效率.

3 基于構造的重構優化方法

隨著混合重構原理的提出，學術界出現了大量基于混合重構思想的單磁盤錯誤重構優化方法.現有的單磁盤錯誤重構優化方法大致可分為2類：基于構造的優化算法和基于搜索的優化算法.其中，基于構造的重構算法主要以數學方法構造，包括針對RDP碼的RDOR(row diagonal optimal recovery)算法[8]、evenodd碼的重構優化算法[35]和X碼的MDRR(minimum disk read recovery)算法與GMDRR(group-based minimum disk read recovery)算法[36]等.本節先詳細介紹RDOR算法、MDRR算法和GMDRR算法，然后再從總體上對基于構造的重構算法進行對比與分析，最后給出各算法的意義與應用場景.

3.1 RDOR算法

RDOR算法是最早的基于糾刪碼的單磁盤錯誤重構優化算法.由于該算法針對RDP碼進行優化，本文先介紹RDP碼的基本結構.圖5給出了1個6磁盤RDP碼的例子，其中包含2種不同的校驗元素，為了方便區分，本文稱圖5(a)所示的校驗元素為水平校驗元素，稱圖5(b)所示的校驗元素為反對角校驗元素.

Fig. 5 6-disks RDP code圖5 6-磁盤RDP碼

Fig. 6 An example of RDOR algorithm圖6 RDOR算法的例子

3.2 MRDD算法與GMDRR算法

雖然RDOR算法僅針對RDP碼，但由于橫式編碼的重構優化構造原理十分相似，因此針對其他橫式編碼基于構造的優化算法與RDOR算法十分接近，例如文獻[35]中針對EVENODD碼的優化算法等.此外，根據RDOR算法的思想，甚至可以較容易地推導出其他一些橫式編碼(例如Liberation碼)的構造算法.然而，對于縱式編碼，RDOR算法的思想則不完全適用.為此，文獻[36]在典型縱式編碼X碼的基礎上，首先提出了一種用于優化讀取數據總量的MDRR算法，隨后又提出了一種將條帶映射到物理磁盤的方法，并以此為基礎提出了能夠達到磁盤間負載均衡的GMDRR算法.下面先介紹X碼的基本結構：如圖7所示，X碼包含2種校驗元素，其中，由斜率為1所在直線上的數據元素計算得來的校驗元素被稱為對角校驗元素，由斜率為-1所在直線得數據元素計算而來得校驗元素則被稱為反對角校驗元素.

Fig. 7 5-disks X-Code圖7 5-磁盤X碼

MDRR算法主要包含2個步驟：

1) 當0≤i≤(p-5)/2時，若i為奇數，則用反對角校驗元素重構di,f，否則用對角校驗元素重構di,f.

2) (p-3)/2≤i≤p-1當時，若i為偶數，則用反對角校驗元素重構di,f，否則用對角校驗元素重構di,f.

下面通過一個具體的案例，對MDRR算法的運行機制進行分析：在圖7所示的X碼中，若磁盤D0出錯，根據MDRR算法，由于(p-5)/2=0，因此當i=0時，用對角校驗元素所在的原始等式重構d0,0；當i=1,2,3,4時，用反對角校驗元素所在的原始等式重構d1,0和p3,0，然后再用對角校驗元素所在的原始等式重構d2,0和p4,0.

與RDOR算法相比，MDRR算法雖然也能夠達到理論最少的數據讀取總量，但無法達到磁盤間的負載均衡.為此，文獻[36]進行了更深入的研究，并進一步證明：在保證讀取數據量最少的前提下，X碼的1個條帶中不存在能夠達到磁盤間負載均衡的算法(包含7塊磁盤的X碼除外).隨后提出了GMDRR算法，該算法在MDRR算法的基礎上，進一步提出了一種用于構造條帶棧的方法，從而達到磁盤間的負載均衡.GMDRR算法的主要步驟如下：

1) 設置p-1個連續條帶，記為條帶1，條帶2，…,條帶p-1.

2) 在條帶l(1≤l≤p-1)中，將D〈k×l〉p映射到第k塊物理磁盤.

在圖7所示的X碼中，GMDRR需要設置4個連續條帶，然后按照給定規則在各條帶的內部，將各個條塊(Dk)映射到不同的物理磁盤中.若用PDk來標識不同的物理磁盤，那么在條帶3中，D4將被映射到PD2.各條塊與物理磁盤的映射關系如圖8所示(由于X碼沒有專門的校驗條塊，所有的條塊都被認為是數據條塊).

Fig. 8 Stack for GMRDD algorithm圖8 GMDRR算法中的條帶棧

GMDRR算法的實現原理與MDRR相同，在此不再贅述.理論推導證明：GMDRR算法不但能夠達到最少的數據讀取量，而且還能讓各磁盤的I/O負載達到均衡.

3.3 構造算法對比

3.1～3.2節主要介紹了RDOR算法(基于橫式編碼的構造算法)、MDRR算法和GMDRR算法(基于縱式編碼的構造算法)各自的構造細節.在實際應用中，它們也分別代表2類不同編碼(即橫式編碼與縱式編碼)的構造思路.橫式編碼的構造算法以RDOR算法為代表，通常先隨機選擇一些失效數據元素，并用水平校驗元素進行重構，其他失效數據元素則用對角/反對角校驗元素進行重構；隨后，利用一些數學手段，通過構造的方式證明只要滿足上述條件的可行解，其讀取數據總量一定為理論最優；最后再建立一些輔助集合，從上述讀取數據量最優的可行解中找到1個能夠達到負載均衡的可行解.

與針對橫式編碼的重構方法相比，針對縱式編碼的重構方法雖然也以讀取數據總量和磁盤見負載均衡為優化目標，但構造讀取數據總量最優的可行解的難度較大，主要體現在2個方面：

1) 在橫式編碼可行解的構造過程中，通常先用一定數量的水平校驗元素重構部分失效元素，然后用對角/反對角校驗元素重構其他失效元素.當這個數量為某一固定值時，所產生的所有重構方案所需讀取的數據總量一致且最優，解空間相對較小；然而在縱式編碼中，上述結論并不成立，因此構造難度較大，甚至有時候需要針對具體的磁盤數進行分析，才能找到讀取數量總量最優的可行解.

2) 橫式編碼通常具有較好的負載均衡，然而在縱式編碼中，有可能不存在能夠達到磁盤間完全均衡的可行解，因此構造負載均衡的可行解的難度非常大，甚至可能要證明該編碼不存在負載均衡的可行解，然后再通過一些數學手段，在條帶棧級構造能夠達到負載均衡的可行解.

總之，基于構造的單磁盤錯誤重構方法可根據其針對的編碼類型分為2類，分別可針對一些典型的橫式編碼和縱式編碼構造理論最優的重構方案.由于這些方案的構造難度較大，目前主要針對一些典型的RAID-6編碼，且僅對編碼的標準形態有效，因此普適性較差，主要適用于一些采用典型編碼標準形態的存儲系統，以及為基于搜索的單磁盤錯誤重構方法的理論分析提供重要依據.

4 基于搜索的重構優化方法

針對基于構造的優化方法普適性差的缺點，研究者們提出了許多基于搜索的優化方法，這些方法對所有基于異或運算的糾刪碼都有效.根據搜索復雜度的不同，基于搜索的單磁盤錯誤重構方法可分為NP-Hard級搜索算法和多項式級搜索算法2類.

4.1 NP-Hard級搜索算法

文獻[37]首先提出了一種基于搜索的單磁盤錯誤重構方法，該方法用計算機作輔助工具，利用深度優先搜索原理，遍歷解空間內所有可行的重構方案，從而找到讀取數據總量最少的可行解.該方法主要包含3個步驟：

1) 利用糾刪碼的原始等式，為各失效元素構建重構等式，然后再構建能夠重構所有失效元素的可行解.顯然，若失效的條塊中包含w個元素，則所有可行解都由w個重構等式構成，每個重構等式用于重構1個失效元素.在圖3所示的編碼中，由式(9)(12)(15)和式(10)(12)(16)構成的重構方案都是潛在的可行解.

2) 將所有的可行解構造成搜索樹結構.首先設置起始節點S，然后將第1個失效元素的所有重構等式放置在第2層，作為起始節點的子節點；若第2層包含a個節點，則將第2個失效元素的所有重構等式復制a份，并放置在第3層，每份副本中的所有重構等式均連接相同的第2層節點；依此類推，直到最后1層的重構等式放置完畢為止.在圖3所示的例子中，若D1發生錯誤，所形成的搜索樹如圖9所示:

Fig. 9 Search tree for recovery圖9 用于重構的搜索樹

3) 遍歷搜索樹中所有的可行解，并從中找到讀取數據量最少的解；在搜索過程中可以利用啟發式搜索算法的思想對搜索樹進行剪枝處理，例如算法可以記錄當前最優解的讀取數據量，在搜索過程中，一旦某個方案的數據讀取量大于或等于最優解的數據讀取量，那么立即放棄該方案，不再向葉子節點繼續搜索.在圖3所示的編碼中，該算法首先找到由等式(9)(11)(14)組成的可行解，其讀取數據總量為9，記錄下當前解；接著再搜索下一個可行解，由等式(9)(11)(15)構成，將它的讀取數據總量與當前搜索結果中最小的讀取數據總量進行對比，發現其讀取數據總量為7，小于當前最小讀取數據總量9，于是記錄下這組可行解；接著再搜索下一組可行解，直到解空間搜索完畢.由于沒有出現讀取數據總量更小的解，由等式(9)(11)(15)構成的解決方案就是讀取數據量最小的可行解.

文獻[37]算法的核心思想在于讓讀取數據總量最小.然而，在云存儲系統/磁盤陣列中，由于所有磁盤都支持并行讀取，重構過程(利用重構等式計算出失效元素)通常要等待所有待讀取元素都進入內存后才能開始，因此在各元素容量較大的情況下，系統設計者要考慮的首要問題是如何提高讀速最慢磁盤的I/O效率.針對此問題，研究者們提出了一些優化磁盤間負載均衡的解決方案，具體可分為條帶級負載均衡優化算法和條帶棧級負載均衡優化算法2類.

條帶級負載均衡優化算法以“條帶”為基本重構單位，主要包括文獻[38]提出的C算法、U算法等.其中，C算法核心步驟與文獻[37]算法比較類似，其主要區別在于：在遍歷所有可行解的過程中，C算法不但要記錄當前讀取數據總量最小的解決方案，而且還要記錄該解中負載最大磁盤所需讀取的數據量，若新搜索到的某個解決方案所需讀取的數據總量與當前最優的解決方案相同，而此方案中負載最重磁盤所需讀取的數據量更少，則用新搜索到的方案作為當前最優方案，例如若當前最優方案總共需要讀取26個元素，其中負載最重磁盤需要讀取6個元素，當搜索到某個解決方案需要讀取26個元素，且負載最重磁盤僅需讀取5個元素時，則用新搜索到的解決方案替換當前的最優解.U算法在搜索決策樹的過程中以負載均衡為首要目標，例如，若當前最優解總共需要讀取26個元素，負載最重磁盤需要讀取5個元素，當出現某個解共需讀取27個元素，而負載最重磁盤只需讀取4個元素時，則用新搜索到的解決方案替換當前最優解.

條帶棧級負載均衡優化算法主要針對循環移動的條帶棧，以“條帶棧”為最小重構單位，主要包括BP算法[39]等.BP算法分為2個主要部分：1)跟文獻[37]方法類似，首先構建失效元素的重構等式，然后根據重構等式在各條帶內部以搜索樹的形式構建解空間；隨后，BP算法將在各條帶內部，按照文獻[37]提出的方法進行搜索.不同的是，文獻[37]方法僅記錄讀取數據總量最小的解，而BP算法會為讀取數據總量設定閾值α，并記錄所有在讀取數據總量在(最小讀取數據總量+α)范圍內的解決方案.例如，若某個條帶中讀取數據總量最少的解決方案需要讀取27個數據元素，α=1，BP算法則會在各個條帶中記錄讀取數據總量小于或等于28的所有解決方案.2)利用模擬退火算法的思想，首先在1個條帶棧的各條帶中隨機選擇1個解決方案，所生成的條帶棧級解決方案也被稱之為初始解，并將當前最優解設定為該初始解；此后，根據整個條帶棧中各磁盤的負載均衡程度，設定1個懲罰函數，并計算該條帶棧級解決方案的懲罰因子；接著再隨機選擇1個或多個條帶，用另一個條帶級解替代該條帶的解，并計算新產生條帶棧級解的懲罰因子，若新產生的條帶棧級解比當前最優解的懲罰因子更小，則用新產生的條帶棧級解替代當前最優解，否則根據當前“溫度”(模擬退火算法中的核心參數之一)，選擇是否替代當前最優解；最后利用模擬退火算法思想重復上述過程，直到出現連續M個解都沒有替換最優解時算法結束，返回當前最優解作為條帶棧級的解決方案.

4.2 多項式級搜索算法

由于NP-Hard級搜索算法需要搜索整個可行解空間，時間復雜度較高，當存儲系統采用的編碼復雜到一定的程度時(例如包含10塊數據磁盤、6塊校驗磁盤的柯西RS碼[25])，這些算法不一定能在規定時間內返回結果.針對此問題，研究者們提出了一些多項式級的搜索算法，根據搜索目標的不同，這些算法大致可歸納為基本搜索算法、優化磁盤I/O的搜索算法和條帶棧級搜索算法3類.

基本搜索算法[40]主要針對云存儲系統，利用貪心算法思想，先構建少量的重構等式，并設定1個初始解；隨后逐步用其他重構等式替代初始解中的某些重構等式，并利用一些貪心算法(例如爬山法、模擬退火算法等)的思想，搜索讀取數據總量最少的可行解，直到找到局部最優解為止.這類算法的時間復雜度通常為多項式級，能夠在較短的時間內找到滿意解.但由于該方法沒有遍歷整個可行解空間，所以不一定能夠找到全局最優解.實驗結果表明:這類算法找到的滿意解與全局最優解在讀取數據總量上非常接近.

優化磁盤I/O的搜索算法主要針對分布式文件系統，其典型特征在于網絡帶寬較充分，但由于各元素所包含的信息量較小，磁盤1次I/O操作可同時讀取多個數據/校驗元素的信息，重構算法可利用磁盤具有較好的“連續讀”性能這一特點進行優化.為此，文獻[9]在文獻[40]方法的基礎上，進一步提出了SIOR算法.SIOR算法在搜索的過程中不但要求讀取數據總量最小，而且還要讓待讀取的數據塊盡量連續.此外，SIOR算法還利用多個條帶之間同時讀取數據的思想，一次性讀取多個條帶中的信息進行重構，從而進一步提高讀取效率.實驗結果顯示，SIOR算法的重構效率明顯優于文獻[40]算法.

條帶棧級搜索算法主要針對循環移動的條帶棧，例如文獻[41]所提出的STP算法等.STP算法在BP算法的基礎上，直接利用條帶棧中所有失效元素的重構等式構造條帶棧級解，然后再通過更換某些失效元素的重構等式，產生新的條帶棧級解決方案，并利用模擬退火算法尋找令人滿意的解決方案.實驗結果顯示，STP算法在條帶棧的應用場景下，相比于文獻[37]算法、C算法和U算法在重構效率上有較大幅度的提升.

4.3 搜索算法對比

基于搜索的重構算法能夠適用于所有基于異或運算的糾刪碼，各算法的主要區別在于不同的優化目標與應用場景以及不同的搜索復雜度.

1) 基于搜索的重構算法可根據搜索過程的時間復雜度分為NP-Hard級算法和多項式級算法2類，其中NP-Hard級搜索算法主要針對磁盤規模較小的糾刪碼，而多項式級重構算法則主要針對磁盤規模較大的糾刪碼或需要實時重構的應用場景.在實際應用中，NP-Hard級算法的重構效率略高于多項式級算法.

2) 根據不同的應用場景，基于搜索的重構算法的優化目標主要有最小化讀取數據總量、最大化磁盤間負載均衡、最大化磁盤的“連續讀”的效果這3類，各算法通常最優化其中1個目標，或者在多個目標之間進行均衡.根據不同的優化目標，現有的搜索算法可分為3類:

① 以最小化讀取數據總量為目標，主要包括文獻[37]算法和文獻[40]算法等.在實際應用中，這類算法主要針對網絡傳輸帶寬較小的云存儲系統/數據中心.由于這些系統中每個數據元素包含的信息較大，其瓶頸在網絡傳輸的時間，因此減少網絡傳輸帶寬有助于總體效率的提升.

② 以同時優化讀取數據總量和磁盤間負載均衡為目標，包括文獻[38]的C算法與U算法、BP算法、STP算法等.這些算法主要適用于網絡帶寬較好的云存儲系統/磁盤陣列，其核心在于利用各磁盤能夠并行讀取數據的特點，將需要讀取的數據元素盡量均勻地分散到不同磁盤中，從而利用數據并行讀的特點減少磁盤I/O的時間，從而提升重構效率.各算法間的區別主要在于均衡點的不同.

③ 以同時優化讀取數據總量和磁盤的“連續讀”為目標，包括文獻[9]的SIOR算法等.這類算法主要針對分布式文件系統，要求各數據元素所包含的信息量不能太大，磁盤的每次I/O操作能夠讀取多個數據/校驗元素，從而利用磁盤的“連續讀”性能遠高于“隨機讀”性能的特點，減少磁盤I/O操作所需的時間，進一步提升重構效率.

各主流搜索算法之間的對比如表1所示:

Table 1 Comparison on Typical Search-Based Recovery Algorithms表1 基于搜索的重構算法對比

3) 根據算法的最小重構單位，基于搜索的重構算法可分為“條帶級”重構算法和“條帶棧級”重構算法2類.在上述的主流算法中，BP算法和STP算法屬于“條帶棧級”算法，其余算法均為“條帶級”算法.在實際應用中，“條帶棧級”算法的重構效率高于“條帶級”算法，但由于“條帶棧級”算法主要針對循環移動各條帶與物理磁盤間映射的場景，適用范圍相對較小.

總之，目前基于搜索的重構方法大都針對實際應用場景而設定優化目標，然后利用重構等式建立搜索樹，最后選擇具有合適復雜度的搜索策略并構建相應的算法.基于搜索的重構方法通常可支持任意基于異或運算的糾刪碼，并能夠在其所針對的應用場景下大幅提升單磁盤錯誤重構性能.

5 用于優化重構效率的新型糾刪碼技術

上述優化方法主要針對已有的糾刪碼，利用混合重構原理進行優化.隨著單磁盤錯誤重構效率問題的提出，研究者們逐漸設計了一些專門用于優化重構效率的新型糾刪碼技術，包括LRC碼[10]、zigzag碼[11]、S2-RAID[42]碼、OI-RAID碼等[43].下面將分類介紹這些新型糾刪碼技術.

1) 用于降低讀取數據總量的糾刪碼技術

這類糾刪碼的主要特征在于：在編碼設計時考慮如何降低單磁盤錯誤重構時所需讀取的數據總量，包括LRC碼、zigzag碼等.其中，LRC碼主要利用分組的思想，將1個條帶中的所有邏輯磁盤分成多個不同的組，每個組內采用RAID-5[44]的方式進行編碼，所產生的校驗元素也被稱為局部校驗元素/組內校驗元素.LRC碼還為所有的數據磁盤構建了全局校驗元素，以提升數據的可靠性.當單個磁盤發生錯誤時，LRC碼只需在錯誤磁盤所在的組內，利用RAID-5的重構方法，就能夠重構所有失效數據.若LRC碼的1個條帶中包含k個數據磁盤、r個校驗磁盤和n個組，則重構每個失效元素所需讀取的數據總量為n/k.

zigzag碼利用混合重構的思想，首先用單位矩陣E生成一些zigzag排列，然后再利用數學手段，在伽羅華域中找出1組線性無關的系數，并利用這些排列和系數，通過伽羅華域中的計算進行編碼.當單個磁盤發生錯誤時，首先根據用于生成編碼排列的單位矩陣的各個行向量，利用一定的數學方法找到合適的原始重構等式，然后再利用伽羅華域中的計算，重構所有的失效元素.理論推導證明，包含k個數據磁盤和r個校驗磁盤的zigzag碼，重構各失效元素所需讀取的數據總量的平均值，能夠達到或接近MDS碼的理論最優值r/k.

2) 用于提升重構并行度的糾刪碼技術

此類糾刪碼主要是在已有糾刪碼的基礎上，通過分組/分層的方式，結合一些數學手段，將多個相同/不同的糾刪碼技術疊加構建.這類糾刪碼主要包括S2-RAID碼、OI-RAID碼等，其中，S2-RAID碼是一種“斜交(skewed)”的RAID-5編碼，它采用分組的方式，首先在各組中處于相同(邏輯)位置的磁盤之間構建RAID-5編碼，然后再采用特定的移位方式，使各組之間的數據/校驗元素產生“斜交”.當單個磁盤發生錯誤時，該編碼可同時利用其他各組中的所有磁盤，并行重構失效元素，從而提升重構效率.

OI-RAID碼則利用分層構造的思想，首先將所有磁盤分為v個組(group)，每組內包含g×g個元素，每個條帶共包含v×r個區域.該編碼碼首先參照BIBD(balanced incomplete block desigin[45])的思想對b個組進行編碼，然后再在每個組內對各對角線上的所有元素做RAID-5編碼.出現單磁盤錯誤時，OI-RAID碼只需所有磁盤(不含錯誤磁盤)并行讀取1個元素，即可重構1個條帶內的所有失效元素.理論推導證明:OI-RAID不但能夠在很大程度上提高重構過程的并行度，而且還能夠容任意3個磁盤錯誤，從而提供很高的數據可靠性.

總之，當前用于優化重構效率的新型糾刪碼技術可根據具體的優化目標分為2類，其中，以降低讀取數據總量為優化目標的糾刪碼具有較高的容錯能力和較低的數據讀取總量，有的還具有MDS屬性，但它們的編/解碼過程通常在伽羅華域中進行，因此編/解碼效率較低.以提升重構并行度的糾刪碼技術采用讓各組之間“斜交”的編碼方式，通過一定的數學方法，讓未出錯的更多磁盤并行地參與到數據重構過程中，從而提升重構過程的并行度，進一步提升數據的重構效率.由于這類技術的編碼過程僅使用異或運算，因此編/解碼效率較高，但由于它們大都采用分組編碼的方式，且各校驗元素都由等量的數據元素生成，因此并沒有在保證相同存儲利用率的前提下降低重構過程中所需讀取的數據總量.

6 總結與展望

本文對目前基于糾刪碼的單磁盤錯誤重構優化方法做了比較全面的總結.首先介紹了糾刪碼的基本概念，隨后介紹了單磁盤錯誤重構的優化原理，接著詳細介紹了現有主流單磁盤錯誤重構優化方法的工作原理.現有的單磁盤錯誤重構優化方法主要包含2類：基于構造的優化方法和基于搜索的優化方法.其中，基于構造的優化方法主要針對一些特定的編碼，利用一些數學手段，以編碼規則為出發點，直接構造能夠達到理論最優的重構方案；基于搜索的優化方法大都通過構建搜索樹的方式，在所有可行的解空間中搜索最優解或滿意解.最后介紹了一些專門針對單磁盤錯誤重構進行優化的新型糾刪碼技術.我們認為，在當前基于糾刪碼的磁盤錯誤重構方法研究中，進一步的研究重點主要包含3個方面：

1) 針對多磁盤錯誤重構的優化技術.隨著存儲規模越來越大，多磁盤同時出錯的概率也將增大，因此，研究多個磁盤同時出錯情況下的數據快速重構技術具有重要意義.

2) 基于異構存儲介質的優化技術.由于云存儲發展的趨勢是存儲介質異構化，磁盤錯誤重構技術還應考慮如何在異構介質下提升重構效率.

3) 針對SSD等新型存儲介質的優化技術.在新型存儲器件中，一些傳統的數據重構優化方法變得不再適用，例如優化數據的“連續讀”等.因此，未來需要針對這些新型存儲介質構建更加適用的重構方法.

[1] Zhiyan Consulting. 2016—2022 China’s big data industry in-depth analysis and investment strategy consulting report, R439946[R]. Beijing: Zhiyan Consulting Group, 2016 (in Chinese)

(智研咨詢. 2016—2022年中國大數據行業深度分析及投資戰略咨詢報告, R439946 [R]. 北京: 智研集團, 2016)

[2] Pinheiro E, Weber W, Barroso L. Failure trends in a large disk drive population[C] //Proc of the 5th USENIX Conf on File and Storage Technologies. Berkeley, CA: USENIX Association, 2007: 17-28

[3] Borthakur D. The Hadoop distributed file system: Architecture and design [EB/OL]. [2017-02-21]. http://hadoop.apache.org/common /docs/current /hdfs-design.html

[4] Hu Yuchong, Chen Henry, Lee P, et al. NCCloud: Applying network coding for the storage repair in a cloud-of-clouds[C] //Proc of the 10th USENIX Conf on File and Storage Technologies. Berkeley, CA: USENIX Association, 2012: 1-8

[5] Ford D, Labelle F, Popovici F, et al. Availability in globally distributed storage systems[C] //Proc of the 10th USENIX Symp on Operating System Design and Implementation. Berkeley, CA: USENIX Association, 2010: 61-74

[6] Calder B, Wang Ju, Ogus A, et al. Windows azure system: A highly available cloud storage service with strong consistency[C] //Proc of the 23rd ACM Symp on Operating Systems Principles. New York: ACM, 2011: 143-157

[7] Facebook. HDFS RAID [EB/OL]. [2017-02-21]. https://wiki.apache.org/hadoop /HDFS-RAID

[8] Xiang Liping, Xu Yinlong, Lui John, et al. Optimal recovery of single disk failures in RDP code storage systems[C] //Proc of the ACM SIGMETRICS 2010. New York: ACM, 2010: 119-130

[9] Shen Zhirong, Shu Jiwu, Fu Yingxun. Seek-efficient I/O optimization in single failure recovery for XOR-coded storage systems[C] //Proc of the 34th Int Symp on Reliable Distributed Systems. Piscataway, NJ: IEEE, 2015: 228-237

[10] Huang Chen, Simitci H, Xu Yikang, et al. Erasure coding in windows azure storage[C] //Proc of the 2012 USENIX Annual Technical Conf. Berkeley, CA: USENIX Association, 2012: 15-26

[11] Tamo I, Wang Zhiying, Bruck J. Zigzag codes: MDS array codes with optimal rebuilding[J]. IEEE Trans on Information Theory, 2013, 59(3): 1597-1616

[12] Schroeder B, Gibson G. Disk failures in the real world: What does an MTTF of 1,000,000 hours mean to you?[C] //Proc of the 5th USENIX Conf on File and Storage Technologies. Berkeley, CA: USENIX Association, 2007: 1-16

[13] Hanfer J, Deenadhayalan V, Kanungo T, et al. Performance metrics for erasure codes in storage systems, RJ 10321[R]. San Jose: IBM Research, 2004

[14] MacWilliams F, Sloane N. The Theory of Error-Correcting Codes[M]. Amsterdam: North Holland, 1977

[15] Reed I, Solomon G. Polynomial codes over certain finite fields [J]. Journal of the Society for Industrial and Applied Mathematics, 1960, 8(2): 300-304

[16] Li Mingqiang, Lee P. STAIR codes: A general family of erasure codes for tolerating device and sector failures in practical storage systems[C] //Proc of the 12th USENIX Conf on File and Storage Technologies. Berkeley, CA: USENIX Association, 2014: 147-159

[17] Plank J, Blaum M, Hafner J. SD Codes: Erasure codes designed for how storage systems really fail[C] //Proc of the 11th USENIX Conf on File and Storage Technologies. Berkeley, CA: USENIX Association, 2013: 95-104

[18] Corbett P, English B, Goel A, et al. Row-diagonal parity for double disk failure correction[C] //Proc of the 3rd USENIX Conf on File and Storage Technologies. Berkeley, CA: USENIX Association, 2004: 1-14

[19] Blaum M, Roth R. On lowest density MDS codes[J]. IEEE Trans on Information Theory, 1999, 45(1): 46-59

[20] Blaum M, Bruck J, Nebib J. Evenodd: An efficient scheme for tolerating double disk failures in RAID architectures[J]. IEEE Trans on Information Theory, 1995, 44(2): 192-202

[21] Plank J. The RAID-6 liberation codes[C] //Proc of the 6th USENIX Conf on File and Storage Technologies. Berkeley, CA: USENIX Association, 2008: 97-110

[22] Plank J. A new minimum density RAID-6 code with a word size of eight[C] //Proc of the 7th IEEE Int Symp on Network Computing and Applications. Piscataway, NJ: IEEE, 2008: 85-92

[23] Blaum M. A family of MDS array codes with minimal number of encoding operations[C] //Proc of the 2006 IEEE Int Symp on Information Theory. Piscataway, NJ: IEEE, 2006: 2784-2788

[24] Huang Chen, Xu Lihao. STAR: An efficient coding scheme for correcting triple storage node failures[C] //Proc of the 4th USENIX Conf on File and Storage Technologies. Berkeley, CA: USENIX Association, 2005: 197-210

[25] Blomer J, Kalfane M, Krap R, et al. An XOR-based erasure-resilient coding scheme[R] Berkeley: International Computer Science Institute, 1995

[26] Xu Lihao, Bruck J. X-Code: MDS array codes with optimal encoding[J]. IEEE Trans on Information Theory, 1999, 45(1): 272-276

[27] Wu Chentao, He Xubin, Wu Guanying, et al. HDP Code: A horizontal-diagonal parity code to optimize I/O load balance in RAID-6[C] //Proc of the 41st Annual IEEE/IFTP Int Conf on Dependable Systems and Networks. Piscataway, NJ: IEEE, 2010: 209-220

[28] Wu Chentao, Wan Shenggang, He Xubin, et al. H-Code: A hybrid MDS array code to optimize large stripe writes in RAID-6[C] //Proc of the 2011 IEEE Int Parallel and Distributed Processing Symp. Piscataway, NJ: IEEE, 2011: 782-793

[29] Shen Zhirong, Shu Jiwu. HV code: An MDS code to improve efficiency and reliability of RAID-6 systems[C] //Proc of the 44th Annual IEEE/IFIP Int Conf on Dependable Systems and Networks. Piscataway, NJ: IEEE, 2014: 550-561

[30] Fu Yingxun, Shu Jiwu. D-Code: An efficient RAID-6 code to optimize I/O loads and read performance[C] //Proc of the 2015 IEEE Int Parallel and Distributed Processing Symp. Piscataway, NJ: IEEE, 2015: 603-612

[31] Hafner J. HoVer erasure codes for disk arrays[C] //Proc of the 2006 IEEE/IFIP Int Conf on Dependable Systems and Networks. Piscataway, NJ: IEEE, 2006: 217-226

[32] Hafner J. WEAVER codes: Highly fault tolerant erasure codes for storage systems[C] // Proc of the 4th USENIX Conf on File and Storage Technologies. Berkeley, CA: USENIX Association, 2005: 211-224

[33] Luo Xianghong, Shu Jiwu. Summary of research for erasure code in storage system[J]. Journal of Computer Research and Development, 2012, 49(1): 1-11 (in Chinese)

(羅象宏, 舒繼武. 存儲系統中的糾刪碼研究綜述[J]. 計算機研究與發展, 2012, 49(1): 1-11)

[34] Greenan K, Li Xiaozhou, Wylie J. Flat XOR-based erasure codes in storage systems: Constructions, efficient recovery, and tradeoffs[C] //Proc of the 26th IEEE Symp on Mass Storage Systems and Technologies. Piscataway, NJ: IEEE, 2010: 1-14

[35] Wang Zhiying, Dimakis A, Bruck J. Rebuilding for array codes in distributed storage systems[C] //Proc of 2010 IEEE GLOBALCOM Workshops. Piscataway, NJ: IEEE, 2010: 1905-1909

[36] Xu Silei, Li Runhui, Lee P, et al. Single disk failure recovery for X-code-based parallel storage systems[J]. IEEE Trans on Computers, 2013, 63(4): 995-1007

[37] Khan O, Burns R, Plank J, et al. Rethinking erasure codes for cloud file systems: Minimizing I/O for recovery and degraded reads[C] //Proc of the 10th USENIX Conf on File and Storage Technologies. Berkeley, CA: USENIX Association, 2012: 1-14

[38] Luo Xianghong, Shu Jiwu. Load-balanced recovery schemes for single-disk failure in storage systems with any erasure code[C] //Proc of the 2013 Int Conf on Parallel Processing. Piscataway, NJ: IEEE, 2013: 552-561

[39] Fu Yingxun, Shu Jiwu, Luo Xianghong. A stack-based single disk failure recovery scheme for erasure coded storage systems[C] //Proc of the 33rd IEEE Symp on Reliable Distributed Systems. Piscataway, NJ: IEEE, 2014: 136-145

[40] Zhu Yunfeng, Lee P, Hu Yuchong, et al. On the speedup of single-disk failure recovery in XOR-coded storage systems: Theory and practice[C] //Proc of the 28th IEEE Symp on Mass Storage Systems and Technologies. Piscataway, NJ: IEEE, 2012: 1-12

[41] Fu Yingxun, Shu Jiwu, Shen Zhirong. Reconsidering single disk failure recovery for erasure coded storage systems: Optimizing load balancing in stack-level[J]. IEEE Trans on Parallel and Distributed Systems, 2017, 27(5): 1457-1469

[42] Wan Jiguang, Wang Jibin, Yang Qing, et al. S2-RAID: A new raid architecture for fast data recovery[C] //Proc of the 26th IEEE Symp on Mass Storage Systems and Technologies. Piscataway, NJ: IEEE, 2010: 1-9

[43] Wang Neng, Xu Yinlong, Li Yongkun, et al. OI-RAID: A two layer raid architecture towards fast recovery and high reliability[C] //Proc of the 2016 IEEE/IFIP Int Conf on Dependable Systems and Networks. Piscataway, NJ: IEEE, 2016: 61-72

[44] Patterson D, Gibson G, Katz R. A case for redundant arrays of inexpensive disks (RAID)[C] //Proc of the 1988 ACM Special Interest Group on Management of Data. New York: ACM, 1988: 109-116

[45] Hall M. Combinatorial Theory[M]. Hoboken, NJ: John Wiley & Sons, 1998