VMD結合誤差能量算法在管道泄漏檢測中的應用①

梁洪衛 鄒岱峰 高丙坤 闞玲玲

(東北石油大學電氣信息工程學院)

VMD結合誤差能量算法在管道泄漏檢測中的應用①

梁洪衛 鄒岱峰 高丙坤 闞玲玲

(東北石油大學電氣信息工程學院)

為了實現對管道泄漏信號的去噪并進行有效信息的提取，使用變分模態分解(VMD)結合誤差能量算法對管道信號進行處理。首先，對采集到的信號進行VMD處理，得到一系列IMF(原始信號經過VMD分解后的分量)。然后，對提取到的IMF的概率密度函數進行誤差能量計算，比較所得的誤差能量大小，篩選合適的IMF。最后，把所有滿足條件的IMF疊加起來，重構原始信號去噪后的有效信息。

VMD算法 誤差能量算法 管道泄漏 有效信息提取 IMF

近年來，利用管道運輸石油和天然氣在國內外得到了廣泛應用，因此管道安全與防泄漏成為備受關注的問題。造成管道泄漏的原因很多，如非法入侵、打孔盜油、自然災害及管道老化等。目前，管道泄漏檢測方法主要有高頻端聲壓檢測法、小波變換法及經驗模態分解(Empirical Mode Decomposition，EMD)法等[1，2]。其中，EMD法是廣泛使用的一種管道泄漏檢測方法，但是EMD算法存在一些不可避免的缺陷，如EMD對噪聲和采樣靈敏度具有局限性，EMD的數學算法問題限制了理論的發展和分解穩固性的改進。因此，變分模態分解(Variational Mode Decomposition，VMD)算法應運而生[3]。

VMD算法是一種可預設尺度的非平穩信號處理方法，它能夠將復雜的復合信號分解為K個子信號，并抑制模態分離混疊現象。在此，筆者使用VMD技術對管道泄漏信號進行處理，然后使用誤差能量方法挑選有效子信號，以達到精確檢測的目的。

1 VMD算法

VMD算法通過迭代搜索變分模型最優解來確定每個分量的中心頻率與帶寬，進而獲取分解分量。

1.1 維納濾波

維納濾波是一種基于最小均方誤差準則和對平穩過程的最優估計器。這種濾波器的輸出與期望輸出之間的均方誤差最小，因此，維納濾波器是一個最佳濾波系統，可用于提取被平穩噪聲所污染的信號。

假設有一個觀察信號f0，它通常由待測信號f和均值為0的高斯噪聲信號η構成，即：

f0=f+η

(1)

恢復待測信號f通常采用吉洪諾夫正則化方法[4～6]：

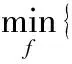
(2)

其中，α為白噪聲的方差(如果噪聲不是白噪聲而是有色噪聲，則對該有色噪聲進行白化處理)，?t為f對時間t的偏導。通過歐拉-拉格朗日方程做簡單變換，在其傅里葉域求解：

(3)

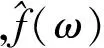
1.2 希爾伯特變換

在數學與信號處理領域中，一個實值函數的希爾伯特變換是將信號s(t)與1/πt做卷積，以得到s′(t)。因此，希爾伯特變換結果s′(t)可以被解讀為輸入是s(t)的線性時不變系統的輸出，因此系統的脈沖響應為1/πt。

1.3 解析信號

在能量不變的前提下，利用希爾伯特變換構造一個虛部，使之只有正頻譜，即：

z(t)=u(t)+jv(t)

(4)

其中，u(t)是一個實信號，v(t)是u(t)的希爾伯特變換，z(t)是解析信號。在實信號分析中，利用構建解析信號的方法，可以得到一個實信號在復空間的映射，解析信號的實部與虛部互為希爾伯特變換，而希爾伯特變換就是90°相移，因此，解析信號就是實信號自身的一種特殊翻版，采用它可以估計實信號的瞬時頻率，這是在信號分析與處理中構建解析信號的主要目的。

1.4 內稟模態函數

為了使獲得的瞬時頻率有意義，信號必須是單分量信號。為此，研究學者們在研究滿足單分量信號條件的基礎上，提出了內稟模態函數(Intrinsic Mode Function，IMF)的概念。一個IMF必須滿足以下兩個條件：

a. 在整個數據段內，極值點個數與過零點個數必須相等或最多相差一個；

b. 在任意時刻，由局部極大值點形成的上包絡線與由局部極小值形成的下包絡線的平均值需為0。

然而大多數實際信號都無法滿足IMF的兩個條件。因此，為了使獲得的瞬時頻率有意義，需將信號分解為若干個IMF分量。

VMD算法的目的是分解一個實值輸入信號到若干個離散的子信號(模態)。VMD分解步驟如下：

a. 對每個模態函數uk通過希爾伯特變換計算出相關的解析信號，以獲得單邊頻譜；

b. 利用指數修正，移動模態函數的頻譜到各自估算的中心頻率；

c. 對解調信號進行高斯平滑[8](即L2范數梯度的平方根)，以得到各模態函數的帶寬。

此時，各模態的分解就轉換成了一個變分問題，即：

(5)

其中，{uk}是所有子分量的集合，{ωk}是所有中心頻率的集合，每一個模態k對應一個中心頻率ωk，δ(t)是狄拉克分布。為了解決上述約束最優化問題，VMD算法在實施過程中利用了二次懲罰項和拉格朗日乘子，引入了增廣拉格朗日函數L：

L({uk},{ωk},λ):=ukn+1

(6)

其中，λ(t)是拉格朗日乘子。使用交替方向乘子法，通過對式(6)進行計算，并根據Plancherel定理，L2范數問題就可以等距轉換到其傅里葉變換上，最終得到：

(7)

其中，1/(ω-ωk)2是維納濾波的電流殘差。同理，可以計算出中心頻率ωk，其極小值為：

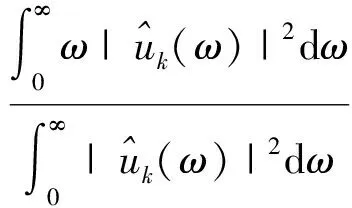
(8)

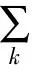
VMD算法的最大難點在于挑選有效的IMF，這樣才能精確還原原始信號中的有用信息。在此，筆者使用誤差能量算法來挑選有效的IMF。

2 誤差能量算法

2.1 概率密度函數

連續型隨機變量的概率密度函數是一個描述該隨機變量的輸出值在某個確定的取值點附近的可能性的函數。概率密度函數是隨機變量的另一種表示形式。

2.2 原理

在信號處理中，若要描述兩個信號的相似性，最直觀的辦法就是將兩個信號相減，計算兩者的誤差能量。如果誤差能量為0，說明兩個信號完全一致。誤差能量越大，則兩個信號越“不像”。如果兩個信號是同頻的單頻正弦信號，一個幅度為2，另一個幅度為1，此時只做簡單的判斷是不可行的。為此，假定第1個信號為S1(n)，第2個信號為S2(n)，然后構造誤差信號v(n)：

v(n)=S1(n)-AS2(n)

(9)

其中，A為信號縮放系數。則誤差能量Ev為：

Ev=∑v2(n)=∑[S1(n)-AS2(n)]2

=E1-2A·∑S1(n)·S2(n)+A2·E2

(10)

其中，E1是信號S1(n)的能量，E2是信號S2(n)的能量。為了使Ev最小，通過簡單的微積分運算可知，此時A的取值為：

A=∑S1(n)·S2(n)/E2

(11)

如果將兩個信號的相關函數C定義為：

C=∑S1(n)·S2(n)

(12)

則此時的誤差能量為：

Ev=E1-C2/E2

(13)

3 實驗與仿真分析

實驗數據從管道泄漏檢測實驗室采集，實驗室仿真管道總長160m，管徑DN5mm，管壁厚20mm，管道內可以實現氣體和液體的運輸。實驗采用壓縮空氣法，LabVIEW設置采樣頻率為1kHz，通過采集卡采集泄漏的聲信號，并將信號傳送至工控機中進行處理，由Matlab將采集的信號數據進行VMD分解，然后對低頻特征模態進行識別，判斷是否發生泄漏。

管道的泄漏信號(無敲擊)、敲擊信號(無泄漏)和正常信號分別如圖1所示。

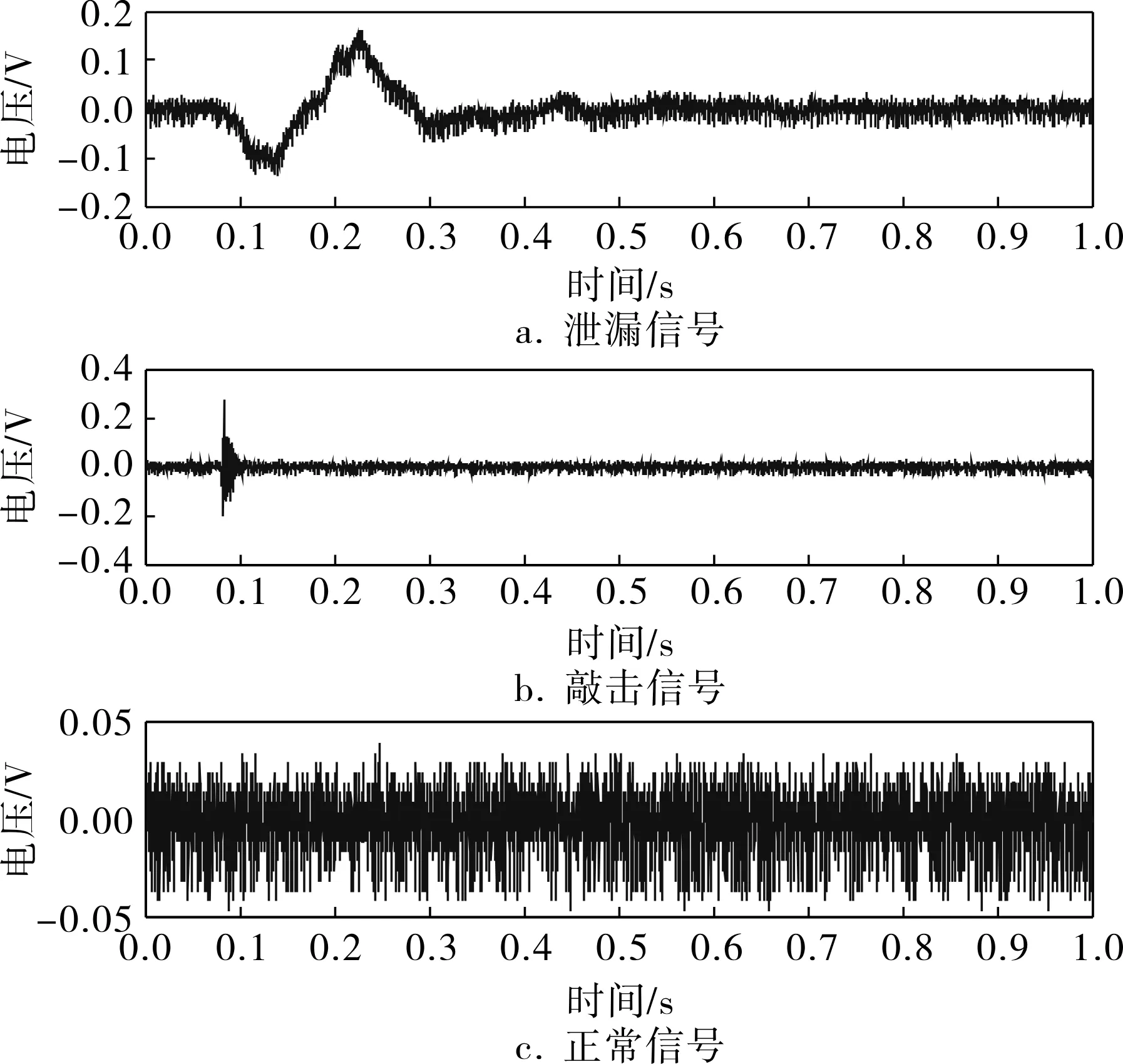
圖1 3種管道信號

在實際檢測過程中，測量環境必然是復雜且充滿噪聲的，為了盡可能與實際情況一致，實驗模擬了在檢漏過程中不斷敲擊的信號，如圖2所示。實驗的目的是在這個復雜的復合信號中提取有用信息。從圖2可以看出，該信號是一個泄漏信號，但是含有大量噪聲和敲擊信號干擾，接下來將使用VMD結合誤差能量算法對該信號進行處理。

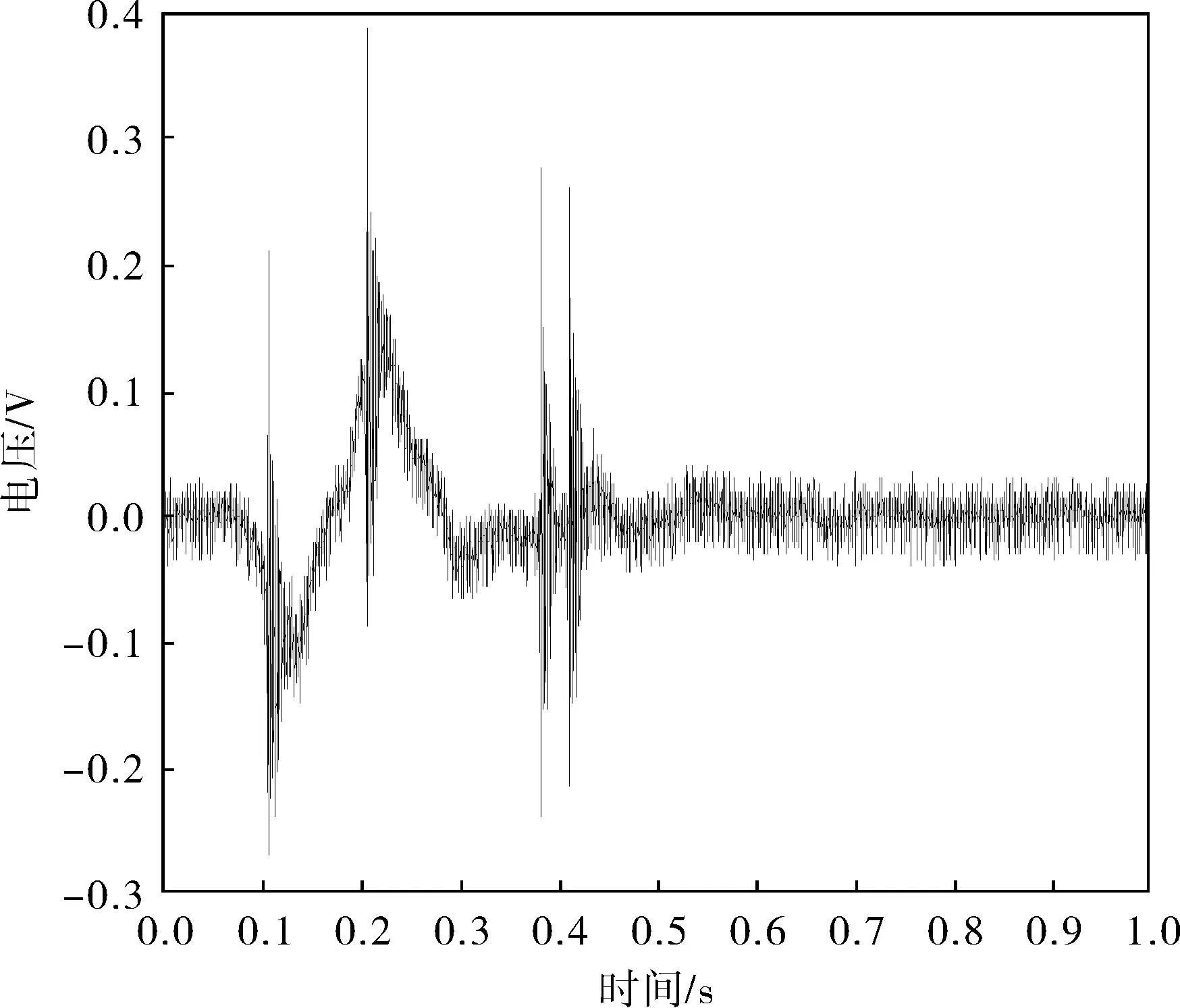
圖2 模擬的實際信號

預設度值為9，可以得到如圖3所示的各IMF分量，對它們進行誤差能量計算，結果見表1。

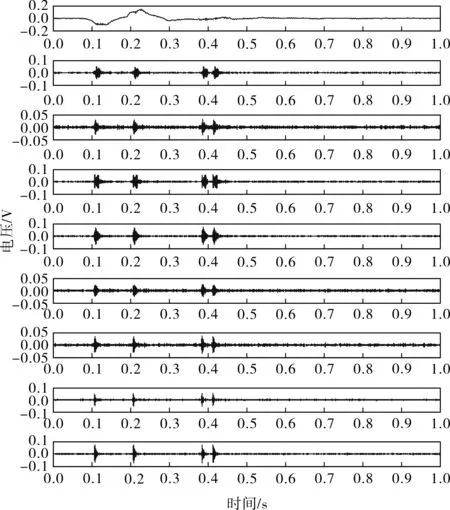
圖3 VMD分解模態

表1 誤差能量

從表1可以看出，第1個IMF分量為有效信號，該信號的重構信號如圖4所示。可以看出，該重構信號并沒有受到敲擊信號等噪聲的影響，準確地得到了泄漏信號，表明VMD結合誤差能量算法可以有效、精確地檢測出管道泄漏信號。

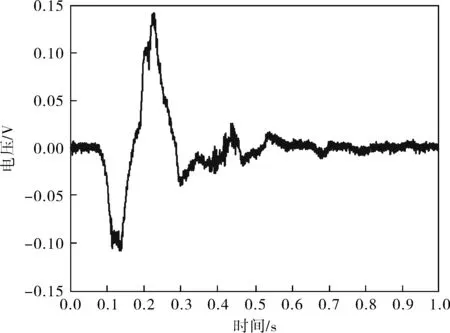
圖4 IMF1的重構信號

在實際檢測過程中，信號與噪聲更加不規則，并且信號強度也比實驗數據更大，所以會得到較大的數據，對數據分析主要是尋找信號誤差能量急劇增大的點，從而確定有效的IMF。

4 結束語

筆者使用VMD結合誤差能量算法從含有大量噪聲的管道泄漏信號中提取有效信息。VMD方法是一種新穎的變分方法，可以將信號分解成有限帶寬的IMF。實驗結果表明，無論是實驗數據還是實際數據，VMD結合誤差能量算法都能夠準確地提取出有效信息。與傳統方法相比，該方法更加靈敏、準確，具有一定的應用前景。

[1] 王秀芳,檀麗麗,高丙坤,等.變分模態分解和相關系數聯合算法在管道泄漏檢測中的應用[J].壓力容器,2016,33(12):59～63.

[2] 沈繼忱,王春雨,王慧麗.管道泄漏診斷方法研究[J].化工自動化及儀表,2012,39(3):309～312.

[3] 王振威.基于變分模態分解的故障診斷方法研究[D].秦皇島:燕山大學,2015.

[4] 林小芳.幾種濾波算法的比較研究[J].福建電腦,2017,33(2):107.

[5] 趙振宇,由雷.求解熱源識別問題的修正吉洪諾夫正則化方法[J].數學物理學報,2014,34(1):186～192.

[6] 虞貴財,邵玉斌,肖笛.產生高斯白噪聲的研究與實現[J].電子科技,2006,(11):16～18.

[7] Dragomiretskiy K,Zosso D.Variational Mode Decomposition[J].IEEE Transactions on Signal Processing,2014, 62(3):531～544.

[8] 李雪威,張新榮.保持邊緣的高斯平滑濾波算法研究[J].計算機應用與軟件,2010,27(1):83～84.

ApplicationofVMDCombinedwithErrorEnergyAlgorithminPipelineLeakageDetection

LIANG Hong-wei , ZOU Dai-feng, GAO Bing-kun, KAN Ling-ling
(CollegeofElectricalEngineeringandInformation,NortheastPetroleumUniversity)

In order to denoise the pipeline leakage signals and extract effective information, making use of VMD combined with error energy algorithm to process the pipeline signals was implemented, including applying VMD (variational modal decomposition) to process signals acquired so as to obtain a series of IMFs (the components obtained by the VMD decomposition of the original signal), and then calculating the error energy of the IMF's probability density function and comparing their error energy and screening appropriate IMF, as well as superimposing all ideal IMF to reconstruct the effective information of original signals denoised.

VMD algorithm, error energy algorithm, pipeline leakage, extracting effective information,IMF

黑龍江省自然科學基金項目(E2016013)。

梁洪衛(1978-)，副教授，從事油氣信息處理的研究。

聯系人鄒岱峰(1993-)，碩士研究生，從事油氣信息處理的研究，372836687@qq.com。

TH865

A

1000-3932(2017)12-1110-04

2017-08-13，

2017-08-25)