多粒度粗糙集粒度約簡的高效算法

胡善忠，徐 怡,2，何明慧，王 冉

(1.安徽大學 計算機科學與技術學院，合肥 230601； 2.計算智能與信號處理教育部重點實驗室(安徽大學)，合肥 230039)

多粒度粗糙集粒度約簡的高效算法

胡善忠1，徐 怡1,2*，何明慧1，王 冉1

(1.安徽大學 計算機科學與技術學院，合肥 230601； 2.計算智能與信號處理教育部重點實驗室(安徽大學)，合肥 230039)

針對已有多粒度粗糙集粒度約簡算法效率較低的問題，提出一種多粒度粗糙集粒度約簡的高效算法(EAGRMRS)。首先，以決策信息系統為對象，定義決策類下近似布爾矩陣，該矩陣能夠將粒度約簡過程中過多且有重復的集合運算轉換為布爾運算，基于該矩陣給出計算決策類下近似算法和計算粒度重要度算法。然后，針對計算粒度重要度時存在冗余計算的問題，提出粒度動態增加時快速計算粒度重要度的算法，并在此基礎上，提出EAGRMRS，該算法的時間復雜度為O(|A|·|U|2+|A|2·|U|)，其中|A|表示粒度集合大小，|U|表示決策信息系統中實例數。在UCI數據集上的實驗結果驗證了所提算法的有效性和高效性，并且隨著數據集的增大，EAGRMRS相較于多粒度粗糙集粒度約簡的啟發式算法(HAGSS)效率優勢更加明顯。

多粒度粗糙集；布爾矩陣；信息系統; 重要度；粒度約簡

0 引言

粗糙集理論是波蘭數學家Pawlak[1]提出的能有效處理不精確、不一致和不完備數據的方法，目前，粗糙集理論已廣泛用于機器學習、數據挖掘、特征選擇等領域[2-4]。從粒計算的角度看，經典的粗糙集模型是基于單粒度和單層次的，無法從多粒度、多層次的角度分析和處理問題。為了使粗糙集能夠更好地解決實際問題，Qian等[5]提出了多粒度粗糙集，在多粒度粗糙集中，目標決策可以通過多個粒度空間中的信息粒進行刻畫，因此可以從多個角度、多個層次出發分析問題并獲得更加滿意、合理的求解。此后，許多學者提出了基于多粒度粗糙集的擴展粗糙集模型，例如，多粒度優勢關系粗糙集、多粒度模糊關系粗糙集、鄰域多粒度粗糙集、多粒度決策理論粗糙集、可變多粒度粗糙集等[6-10]。這些多粒度粗糙集的擴展模型對粗糙集理論具有重要的推廣作用。

在多粒度粗糙集中，粒度約簡是一個重要問題，通過粒度約簡能夠在保持信息系統決策能力不變的前提下，選擇一個無冗余的粒度空間子集。為了對多粒度粗糙集進行粒度約簡，Qian等[5]首先提出了啟發式的粒度約簡算法，該算法首先基于整個粒度空間對所有粒度按照粒度重要度大小進行排序，然后按序將粒度加入約簡集直到獲得一個粒度約簡結果，但是該算法并沒有給出每步粒度選取時的啟發式函數，且在算法的最后并沒有進一步對約簡集進行冗余粒度的反向消除，獲得的約簡結果可能存在冗余粒度。張明等[10]提出了可變多粒度粗糙集粒度約簡算法，該算法在獲得一個粒度約簡集之后也沒有進一步對約簡集進行冗余粒度的反向消除，所以約簡結果也可能存在冗余粒度。桑妍麗等[11]發展了一種適合悲觀多粒度粗糙集的粒度約簡算法，雖然該算法效率較高，但并不適用于樂觀多粒度粗糙集。此后，Yang等[12]提出了一種多粒度粗糙集粒度約簡的啟發式算法，該算法能獲得約簡率較高的約簡結果，但約簡效率并不高。然而，在實際應用中，面對的往往是數據量很大的決策信息系統，此時，如何提高多粒度粗糙集粒度約簡的效率就成為了一個關鍵問題。

為了提高多粒度粗糙集粒度約簡的效率，本文定義了決策類下近似布爾矩陣，該矩陣能簡化多粒度粗糙集粒度約簡過程中決策類下近似的計算，基于該矩陣給出了計算決策類下近似算法和計算粒度重要度算法，并提出了粒度動態增加時快速計算粒度重要度算法來優化粒度約簡過程中粒度重要度的計算。在此基礎上，本文提出了一種多粒度粗糙集粒度約簡的高效算法(Effective Algorithm for Granulation Reduction of Multi-granulation Rough Set, EAGRMRS)，最后通過實驗驗證了本文所提算法的有效性和高效性。

1 相關概念

在本章，介紹本文用到的相關知識。

定義2[5]設信息系統IS=(U,AT,V,f)，B?AT，對于X?U，X的下、上近似集合和邊界域定義為：

(1)

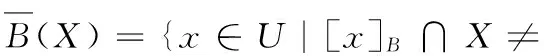
(2)

(3)

其中[x]B是x在B上的等價類。

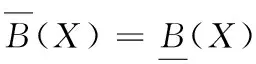
為了能夠從多粒度、多層次的角度分析和處理問題，Qian等[5]提出了多粒度粗糙集。本文中用上標O(Optimistic)表示樂觀的語義，用上標P(Pessimistic)表示悲觀的語義，以此來區分樂觀多粒度粗糙集和悲觀多粒度粗糙集。

定義3[5]設信息系統IS=(U,AT,V,f)，A={A1,A2,…,Am}是AT的m個屬性子集族。對于?X?U，X關于A的樂觀多粒度下近似和樂觀多粒度上近似分別定義如下：

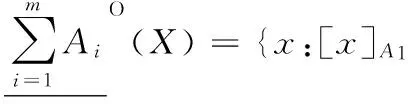
[x]A2?X∨…∨[x]Am?X,x∈U}

(4)

(5)

定義4[5]設信息系統IS=(U,AT,V,f)，A={A1,A2,…,Am}是AT的m個屬性子集族。對于?X?U，X關于A的悲觀多粒度下近似和悲觀多粒度上近似分別定義如下：

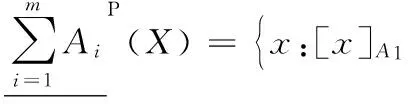
[x]Am?X,x∈U}

(6)

(7)

定義5[13]設決策信息系統DIS=(U,C∪D,V,f)，A={A1,A2,…,Am}是C的m個屬性子集族，決策屬性D導出的劃分為U/D={X1,X2,…,Xr}。用粒度集A表示U/D的近似質量(也稱為依賴度)，定義為：

(8)

2 多粒度粗糙集的粒度約簡

目前，為了滿足不同的需要，已經有許多不同的約簡定義[14-16]被提出，一個常用的定義是保持決策信息系統的正域不變。

定義6[11]設決策信息系統DIS=(U,C∪D,V,f)，A={A1,A2,…,Am}是C的m個屬性子集族，決策屬性D導出的劃分為U/D={X1,X2,…,Xr}，則基于A的樂觀下近似分布函數定義如下：

(9)

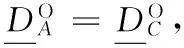
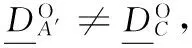
定義8[11]設決策信息系統DIS=(U,C∪D,V,f)，A={A1,A2,…,Am}是C的m個屬性子集族，給定粒度集A′，??A′?A，X∈U/D。

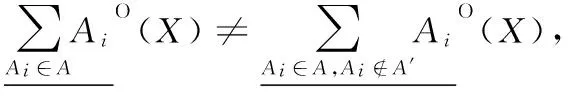
定理1[11]設決策信息系統DIS=(U,C∪D,V,f)，A={A1,A2,…,Am}是C的m個屬性子集族，A′?A，則：

根據定義3，該定理顯然成立。由該定理可知，在樂觀多粒度粗糙集中，隨著粒度空間的增大，下近似中對象的個數增加。在悲觀多粒度粗糙集中，也可以得出類似的結論，隨著粒度空間的增大，下近似中對象的個數減少。因此，可以利用下近似中對象個數的變化來衡量粒度的重要性。

定義9[12]設決策信息系統DIS=(U,C∪D,V,f)，A={A1,A2,…,Am}是C的m個屬性子集族。

1)A′?A，?Ai∈A′，定義在粒度集A′上，Ai關于D的粒度重要度為：

Sigin(Ai,A′,D)=abs(γ(A′,D)-γ(A′-Ai,D))

(10)

2)A′?A，?Ai∈A-A′，定義在粒度集A′上，Ai關于D的粒度重要度為：

Sigout(Ai,A′,D)=abs(γ(Ai∪A′,D)-γ(A′,D))

(11)

其中：abs(N)表示N的絕對值。在粒度約簡的過程中，一般以粒度重要度為啟發來設計粒度約簡算法。

3 多粒度粗糙集粒度約簡的高效算法

3.1 決策類下近似布爾矩陣

粒度約簡中計算粒度重要度時要多次求不同粒度集合下決策類的下近似，為了將過多且有重復的集合運算轉換為布爾運算來提高效率，本文定義了決策類下近似布爾矩陣并給出了根據決策信息系統求決策類下近似布爾矩陣的算法。

該定理顯然成立，對于?x∈U，x僅可能屬于決策類Xk(x∈Xk)的下近似，也就是說x最多屬于一個決策類的下近似。

定義10 設決策信息系統DIS=(U,C∪D,V,f)，U={x1,x2,…,xn},A={A1,A2,…,Am}是C的m個屬性子集族，決策屬性D導出的劃分為U/D={X1,X2,…,Xr}，定義決策類下近似布爾矩陣為M=(M_m(i,j)),其中M_m(i,j)表示第i行第j列的元素(1≤i≤n,1≤j≤m)，元素定義如下：

(12)

其中xi∈Xk(k∈{1,2,…,r})。

決策類下近似布爾矩陣包含|U|行、|A|列，|U|表示決策信息系統中的實例數，|A|表示粒度集合大小。

顯然，決策信息系統的決策類下近似布爾矩陣包含了所有對象在每個粒度上是否屬于對應決策類下近似的信息。這樣，求某個決策類在某個粒度集合上的下近似時我們只需要進行布爾矩陣元素的0、1判斷，不需要再進行集合運算。因此，該矩陣可將粒度約簡中的集合運算轉化為布爾運算。以完備決策信息系統為對象，本文給出計算決策類下近似布爾矩陣的算法。

算法1 計算決策類下近似布爾矩陣算法。

輸入 決策信息系統DIS=(U,C∪D,V,f)，粒度空間A={A1,A2,…,Am}；

輸出 下近似布爾矩陣M。

1)

設置M←?，i←1，j←1；

2)

計算U/D={X1,X2,…,Xr}；

3)

Fori=1 to |U|

Forj=1 tom

If [xi]Aj?Xk

M_m(i,j)=1；

Else

M_m(i,j)=0；

Endif

Endfor

Endfor

4)

輸出M。

該算法的復雜度為O(|A|·|U|2)，建立了上述決策類下近似布爾矩陣以后，粒度約簡算法中計算粒度重要度時，可以基于該矩陣快速計算決策類在任意粒度上的下近似，這個過程只需要簡單地判斷矩陣中元素M_m(i,j)的取值。若M_m(i,j)=0，則對象xi在粒度Aj上不屬于x所在決策類Xk的下近似;若M_m(i,j)=1，則對象xi在粒度Aj上屬于x所在決策類Xk的下近似，避免了過多并且耗時的集合運算。

下面以文獻[17]中的決策信息系統為例，說明構建決策類下近似布爾矩陣的過程。

例1 給定一個決策信息系統DIS=(U,C∪D,V,f),如表1所示，其中:U={x1,x2,x3,x4,x5,x6}為對象集，A={{a1},{a2},{a3},{a4},{a5},{a6}}為粒度空間。

表1 一個完備決策信息系統Tab. 1 A complete decision information system

首先，根據決策屬性導出劃分為U/D={{x1,x2,x3},{x4,x5,x6}}，令X1={x1,x2,x3}，X2={x4,x5,x6}。

然后，對于每個對象xi計算其在每個粒度{aj}上的等價類[x]{aj}并判斷是否包含于對應的決策類，若是，設置矩陣M對應的位置M_m(i,j)=1，否則設置M_m(i,j)=0。對于對象x1，[x1]{a1}={x1,x3,x5,x6}?X1，設置M_m(1,1)=0；[x1]{a2}={x1,x5}?X1，設置M_m(1,2)=0；[x1]{a3}={x1,x3,x4,x5}?X1，設置M_m(1,3)=0；[x1]{a4}={x1,x4,x5,x6}?X1，設置M_m(1,4)=0；[x1]{a5}={x1,x4,x5,x6}?X1，設置M_m(1,5)=0；[x1]{a6}={x1,x2,x3}?X1，設置M_m(1,6)=1。類似，可以計算出x2，x3，x4，x5，x6在粒度{a1}，{a2}，{a3}，{a4}，{a5}，{a6}上的等價類并判斷是否包含于對應的決策類，最終，可以建立如下決策信息系統的決策類下近似布爾矩陣：

接下來以樂觀多粒度粗糙集為例，給出基于決策類下近似布爾矩陣計算決策類下近似算法和基于決策類下近似布爾矩陣計算粒度重要度算法。

算法2 基于決策類下近似布爾矩陣計算決策類下近似算法。

輸入 決策信息系統DIS=(U,C∪D,V,f)，粒度空間A={A1,A2,…,Am}，Xk∈U/D，決策類下近似布爾矩陣M=(M_m(i,j))；

輸出Xk的下近似集合L。

1)

設置L←?，j←1；

2)

?xi∈Xk，

Forj=1 tom

IfM_m(i,j)=1

L←L∪{xi}，break；

Endif

Endfor

3)

輸出L。

然后利用算法2計算決策類下近似，根據定義9易得下面樂觀多粒度粗糙集基于決策類下近似布爾矩陣計算粒度重要度算法。

算法3 基于決策類下近似布爾矩陣計算粒度重要度算法。

輸入 決策信息系統DIS=(U,C∪D,V,f)， 粒度空間A={A1,A2,…,Am}，決策屬性D導出的劃分U/D={X1,X2,…,Xr}，決策類下近似布爾矩陣M=(M_m(i,j))，A′?A，?Ai∈A；

輸出 在粒度集A′上，Ai關于D的粒度重要度SigO。

1)

設置D′←?，D″←?，k←1；

2)

Fork=1 tor

Endfor

3)

IfAi?A′

A″=A′-Ai；

Else

A″=A′∪Ai；

Fork=1 tor

Endfor

4)

基于D′和D″，根據定義9計算SigO；

5)

輸出SigO。

3.2 快速計算粒度重要度算法

文獻[18]中對粒度動態變化時如何快速計算某個對象集的下、上近似進行了研究，提出了一個在粒度動態變化時快速計算下、上近似的算法。而在粒度約簡算法中，選取當前重要度最大的粒度加入約簡集，就涉及粒度動態增加時計算決策類的下近似，基于決策類下近似布爾矩陣，參考文獻[18]可以設計算法來優化計算粒度重要度過程中決策類下近似的計算。

定理3[18]設決策信息系統DIS=(U,C∪D,V,f)，A={A1,A2,…,Am}是C的m個屬性子集族，X?U,有：

(13)

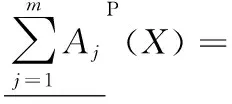
(14)

以樂觀多粒度粗糙集為例，基于決策類下近似布爾矩陣，根據定理3給出粒度動態增加時快速計算決策類下近似算法和粒度動態增加時快速計算粒度重要度算法。

算法4 粒度動態增加時快速計算決策類下近似算法。

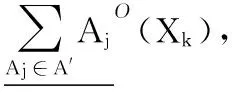
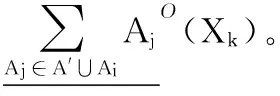
1)

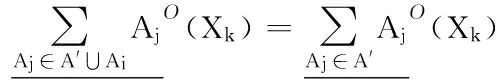
2)

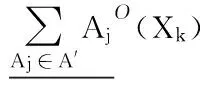
IfM_m(t,i)=1

Endif

3)

基于算法4，得出如下粒度動態增加時快速計算粒度重要度的算法。

算法5 粒度動態增加時快速計算粒度重要度算法。

輸出 在粒度集A′上，Ai關于D的粒度重要度SigO。

1)

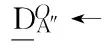
2)

A″=A′∪Ai；

Fork=1 tor

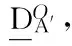
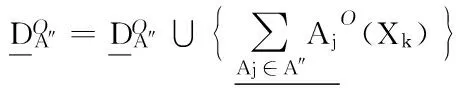
Endfor

3)

4)

輸出SigO。

悲觀多粒度粗糙集中快速計算粒度重要度算法類似，在此不再贅述。

3.3 EAGRMRS

粒度約簡算法的基本過程如下：首先獲得一個原始粒度空間下不可除去的粒度集合(粒度約簡核)，然后以這個粒度集為起點，以粒度重要度為啟發，每次選擇當前粒度空間下最為重要的粒度加入到約簡粒度集中，直到其下近似分布與原始粒度空間下近似分布一致。

算法6 多粒度粗糙集粒度約簡的高效算法(EAGRMRS)。

輸入 決策信息系統DIS=(U,C∪D,V,f)，粒度空間A={A1,A2,…,Am}，決策屬性D導出的劃分U/D={X1,X2,…,Xr}；

輸出 粒度約簡集REDO。

1)

設置REDO←?；

2)

利用算法1建立決策類下近似布爾矩陣M；

3)

對于?Ai∈A，利用算法3計算Sigin(Ai,A,D)，

IfSigin(Ai,A,D)≠0

REDO=REDO∪Ai；

Endif

令COREO=REDO；

4)

Do

IfSigout(Ak,REDO,D)=max{Sigout(Ai,REDO,D):Ai∈A-REDO}

REDO=REDO∪Ak；

Endif

Untilγ(REDO,D)=γ(A,D)；

5)

?Ai∈REDO-COREO

Ifγ(REDO-Ai,D)=γ(A,D)

REDO=REDO-Ai；

Endif

6)

輸出REDO。

算法復雜度分析：第2)步時間復雜度為O(|A|·|U|2)，第3)步時間復雜度為O(|A|2·|U|)，第4)步時間復雜度為O(|A|2·|U|)，所以算法6的時間復雜度為O(|A|·|U|2+|A|2·|U|)。悲觀多粒度粗糙集粒度約簡的高效算法與樂觀多粒度粗糙集粒度約簡的高效算法類似。

4 實驗結果與分析

文獻[12]提出了一種多粒度粗糙集粒度約簡的啟發式算法(Heuristic Approach to Granular Structure Selection, HAGSS)，其中計算決策類下近似可以參考文獻[5]。將本文所提算法EAGRMRS與算法HAGSS進行比較，比較兩種算法的運行效率以及運行效率與數據集包含的數據量的關系。

選用UCI機器學習庫中的4個數據集進行測試，數據集具體信息見表2，其中：數據集Zoo、Chess是完備的，數據集Audiology、Mushroom有缺失的屬性值，是不完備的。對于不完備的數據集等價關系將不再適用，本文中用容差關系來處理不完備的數據集[14]。

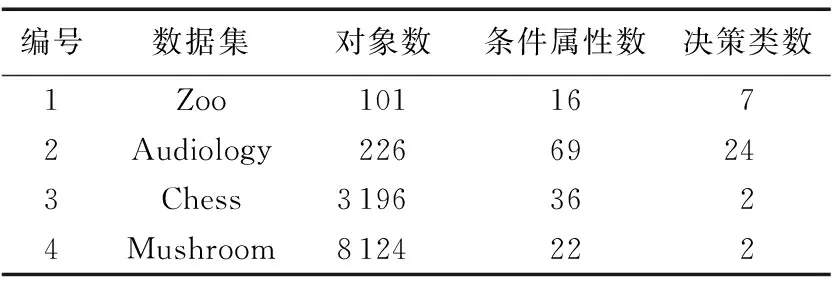
表2 實驗中使用的UCI數據集Tab. 2 UCI datasets used in the experiment

多粒度粗糙集中一個粒度可能包含多個屬性，為了模擬多粒度的情況，對于表2中的數據集，從第一個屬性開始，分別以每1、2、3、4、5個屬性構成一個粒度，若數據集的條件屬性個數不能被1、2、3、4、5整除，最后余下的屬性構成一個粒度，實驗結果如圖1所示。

圖1 不同數據集上不同算法粒度約簡的運行時間Fig. 1 Running time of granulation reduction for different algorithms on different datasets

粒度大小就是構成一個粒度的屬性個數，對于同一個數據集，因為條件屬性一定，所以當選取的粒度大小越大，所組成的粒度空間就越小。從圖1中可以看出，在所有數據集上，算法EAGRMRS進行粒度約簡的運行時間均少于算法HAGSS，且隨著粒度大小變小，也就是粒度空間變大時，HAGSS運行效率下降較為明顯，而算法EAGRMRS運行效率較為穩定。所以，本文所提算法在約簡效率和穩定性方面都優于算法HAGSS。

接下來，為了比較算法EAGRMRS和算法HAGSS的約簡效率與數據集包含的數據量的關系，取粒度大小為3時，四個數據集的約簡時間如圖2所示。

由表2可知，編號為1、2、3、4的數據集包含的數據量是遞增的，由圖2可知，隨著數據集包含的數據量越大，算法HAGSS的運行時間增加得較快，而算法EAGRMRS的運行時間增加較慢，所以在對數據量較大的決策信息系統進行粒度約簡時，本文所提算法效率優勢將更加明顯。

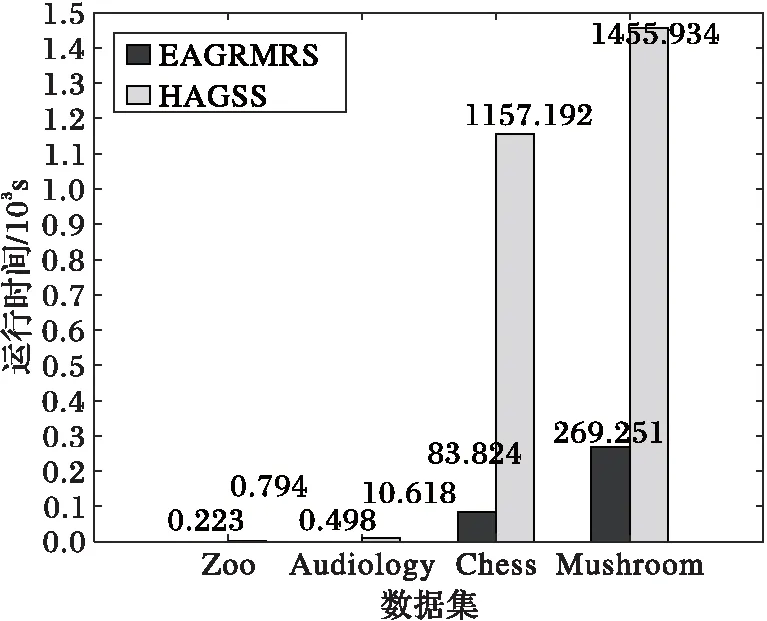
圖2 不同算法在不同數據集上的運行時間Fig. 2 Running time of different algorithms on different datasets

5 結語

本文以決策信息系統為對象，定義了決策信息系統決策類下近似布爾矩陣，該矩陣能簡化多粒度粗糙集粒度約簡過程中決策類下近似的計算，基于該矩陣給出了計算決策類下近似算法和計算粒度重要度算法。此外，針對計算粒度重要度時存在冗余計算，基于決策類下近似布爾矩陣提出了粒度動態增加時快速計算粒度重要度算法，在此基礎上，提出了一種多粒度粗糙集粒度約簡的高效算法(EAGRMRS)。在UCI數據集上的實驗結果驗證了本文所提算法的有效性和高效性。粒度約簡能夠獲得保持決策信息系統決策能力不變的粒度空間子集，如何在粒度約簡之后對每個粒度中的屬性進行進一步的約簡，并對約簡后的決策信息系統進行規則提取是接下來要研究的問題。

References)

[1] PAWLAK Z. Rough sets [J]. International Journal of Computer & Information Sciences, 1982, 11(5): 341-356.

[2] HU Q H, CHE X J, ZHANG L, et al. Rank entropy based decision trees for monotonic classification [J]. IEEE Transactions on Knowledge & Data Engineering, 2012, 24(11): 2052-2064.

[3] SRINIVASA K G, VENUGOPAL K R, PATNAIK L M. A soft computing approach for data mining based query processing using rough sets and genetic algorithms [J]. International Journal of Hybrid Intelligent Systems, 2008, 5(1): 1-17.

[4] 白鶴翔,王健,李德玉,等.基于粗糙集的非監督快速屬性選擇算法[J].計算機應用,2015,35(8):2355-2359.(BAI H X, WANG J, LI D Y, et al. Fast unsupervised feature selection algorithm based on rough set theory [J]. Journal of Computer Applications, 2015, 35(8): 2355-2359.)

[5] QIAN Y H, LIANG J Y, YAO Y Y, et al. MGRS: a multi-granulation rough set [J]. Information Sciences, 2010, 180(6): 949-970.

[6] XU W H, SUN W X, ZHANG X Y, et al. Multiple granulation rough set approach to ordered information systems [J]. International Journal of General Systems, 2012, 41(5): 475-501.

[7] YANG X B, SONG X N, DOU H L, et al. Multi-granulation rough set: from crisp to fuzzy case [J]. Annals of Fuzzy Mathematics and Informatics, 2011, 1(1): 55-70.

[8] LIN G P, QIAN Y H, LI J J. NMGRS: Neighborhood-based multigranulation rough sets [J]. International Journal of Approximate Reasoning, 2012, 53(7): 1080-1093.

[9] QIAN Y H , ZHANG H, SANG Y L, et al. Multigranulation decision-theoretic rough sets [J]. International Journal of Approximate Reasoning, 2014, 55(1): 225-237.

[10] 張明,唐振民,徐維艷,等.可變多粒度粗糙集模型[J].模式識別與人工智能,2012,25(4):709-720.(ZHANG M, TANG Z M, XU W Y, et al. Variable multigranulation rough set model [J]. Pattern Recognition and Artificial Intelligence, 2012, 25(4): 709-720.)

[11] 桑妍麗,錢宇華.一種悲觀多粒度粗糙集中的粒度約簡算法[J].模式識別與人工智能,2012,25(3):361-366.(SANG Y L, QIAN Y H. A granular space reduction approach to pessimistic multi-granulation rough sets [J]. Pattern Recognition and Artificial Intelligence, 2012, 25(3): 361-366.)

[12] YANG X B, QI Y S, SONG X N, et al. Test cost sensitive multigranulation rough set: model and minimal cost selection [J]. Information Sciences, 2013, 250(11):184-199.

[13] 張明,程科,楊習貝,等.基于加權粒度的多粒度粗糙集[J].控制與決策,2015,30(2):222-228.(ZHANG M, CHENG K, YANG X B, et al. Multigranulation rough set based on weighted granulations [J]. Control and Decision, 2015, 30(2): 222-228.)

[14] DAI J H, WANG W T, TIAN H W, et al. Attribute selection based on a new conditional entropy for incomplete decision systems [J]. Knowledge-Based Systems, 2013, 39(2): 207-213.

[15] MIAO D Q, GAO C, ZHANG N, et al. Diverse reduct subspaces based co-training for partially labeled data [J]. International Journal of Approximate Reasoning, 2011, 52(8): 1103-1117.

[16] QIAN J, MIAO D Q, ZHANG Z H, et al. Hybrid approaches to attribute reduction based on indiscernibility and discernibility relation [J]. International Journal of Approximate Reasoning, 2011, 52(2): 212-230.

[17] 鞠恒榮,周獻中,楊佩,等.測試代價敏感的粗糙集方法[J].系統工程理論與實踐,2017,37(1):228-240.(JU H R, ZHOU X Z, YANG P, et al. Test-cost-sensitive based rough set approach [J]. System Engineering — Theory and Practice, 2017, 37(1): 228-240.)

[18] YANG X B, QI Y, YU H L, et al. Updating multigranulation rough approximations with increasing of granular structures [J]. Knowledge-Based Systems, 2014, 64(1): 59-69.

This work is partially supported by the National Natural Science Foundation of China (61402005), the Natural Science Foundation of Anhui Province (1308085QF114), the Higher Education Natural Science Foundation of Anhui Province (KJ2013A015), the Open Foundation of Key Laboratory of Intelligent Computing and Signal Processing at Anhui University of Ministry of Education of China.

HUShanzhong, born in 1990, M. S. candidate. His research interests include rough set theory, granular computing, data mining.

XUYi, born in 1981, Ph. D., associate professor. Her research interests include intelligent information processing, granular computing, rough set theory.

HEMinghui, born in 1991, M. S. candidate. His research interests include neural network, rough set theory.

WANGRan, born in 1993, M. S. candidate. His reseach interests include recommender system, rough set theory.

Effectivealgorithmforgranulationreductionofmulti-granulationroughset

HU Shanzhong1, XU Yi1,2*, HE Minghui1, WANG Ran1

(1.CollegeofComputerScienceandTechnology,AnhuiUniversity,HefeiAnhui230601,China;2.KeyLaboratoryofIntelligentComputingandSignalProcessing,MinistryofEducation(AnhuiUniversity),HefeiAnhui230039,China)

Aiming at the low efficiency problem of the existing granulation reduction algorithms for multi-granulation rough set, an Effective Algorithm for Granulation Reduction of Multi-granulation Rough Set (EAGRMRS) was proposed. Firstly, the lower approximation Boolean matrix of decision classes was defined by using the decision information system as the object. The defined matrix could be used for converting redundant and repeated set operations into Boolean operations in the process of granular reduction. Based on this matrix, the algorithm for computing lower approximation of decision classes and the algorithm for computing the important measure of granularity were presented. Then, focusing on the problem of redundancy calculation when computing the important measure of granularity, a fast algorithm for computing the important measure of granularity with dynamic increasing of granularity was presented. On the basis, the EAGRMRS was proposed. The time complexity of the proposed algorithm isO(|A|·|U|2+|A|2·|U|), in which |A| is the size of granulation set, |U| is the number of instances in decision information system. The experimental results on UCI datasets show that, the proposed algorithm is effective and efficient, the efficiency advantage of EAGRMRS is more obvious over Heuristic Approach to Granular Structure Selection (HAGSS) for multi-granulation rough set when the dataset increases.

multi-granulation rough set; boolean matrix; information system; important measure; granulation reduction

2017- 06- 16;

2017- 09- 07。

國家自然科學基金資助項目(61402005)；安徽省自然科學基金資助項目(1308085QF114)；安徽省高等學校省級自然科學基金資助項目(KJ2013A015)；安徽大學計算智能與信號處理教育部重點實驗室課題項目。

胡善忠(1990—)，男，安徽安慶人，碩士研究生，CCF會員，主要研究方向：粗糙集理論、粒計算、數據挖掘； 徐怡(1981—)，女，安徽滁州人，副教授，博士，主要研究方向：智能信息處理、粒計算、粗糙集理論； 何明慧(1991—)，男，山西晉中人，碩士研究生，主要研究方向：神經網絡、粗糙集理論； 王冉(1993—)，男，安徽合肥人，碩士研究生，主要研究方向：推薦系統、粗糙集理論。

1001- 9081(2017)12- 3391- 06

10.11772/j.issn.1001- 9081.2017.12.3391

(*通信作者電子郵箱xuyi1023@126.com)

TP18

A