基于災變機制的預防性維護和生產調度集成優化方法
吳青松,楊宏兵,方 佳
(蘇州大學 機電工程學院,江蘇 蘇州 215000)
基于災變機制的預防性維護和生產調度集成優化方法
吳青松,楊宏兵*,方 佳
(蘇州大學 機電工程學院,江蘇 蘇州 215000)
為了解決生產車間中多品種任務的生產調度與預防性維護集成優化問題,綜合考慮其加工順序、生產批量及預防性維護策略等要素,在訂單充足的前提下,以總制造成本和加工時間最小化為聯合優化目標,建立了生產調度與預防性維護集成優化模型。針對模型特點,在非支配排序遺傳算法框架的基礎上,基于災變機制和榮譽空間,引入截斷和拼接操作算子,提出一種變長度染色體單親遺傳算法對模型進行求解,并在不同參數條件和問題規模下,通過仿真實驗驗證了該算法解決復雜生產任務調度和預防性維護集成優化問題的有效性。
變長度染色體;災變;生產調度;預防性維護
0 引言
為了利用規模效應,傳統的生產調度往往將一個訂單或者多個相同類型訂單合并集中生產,在這種模型下部分訂單會因較長時間的交貨延遲而導致較高的拖期懲罰,同時集中生產單一產品易導致生產資金的大量占用,因而這種模型已經逐漸不能適應當今生產所呈現的訂單多品種化的趨勢。隨著快速換模技術的發展,通過不同產品產線的快速切換來滿足計劃期內不同訂單需求的生產模式已經被越來越多的生產企業所接受;另一方面,為了平衡各部門的需求和生產中的各種指標,單一的優化目標一般很難滿足實際生產的各種需求,決策者需要綜合考慮多種生產指標以滿足不同的生產狀況,力爭達到整體利益的最大化。在這種情況下,決策過程需要納入多個目標進行綜合考量。
生產調度問題作為一種已經被證實的NP-hard問題:張會紅等[1]運用免疫算法提高調度性能;何法江等[2]提出采用遺傳算法解決并行機器系統工件調度問題;張烈平等[3]將基于慣性權重的粒子群算法應用到了流程工業的生產調度問題中;黃福令等[4]提出了基于改進差分算法和文化算法的混合算法。
上述研究都是針對單一目標進行調度優化,在如實反映生產狀況方面有所欠缺。生產調度和預防性維護多目標集成優化已被越來越多的學者所關注:崔維偉等[5-6]綜合決策工件的加工順序和機器維護方式,并提出相應的算法聯合優化了生產和維修部門各自的目標;吳悅等[7]研究了基于訂單生產模式中訂單完成時間對生產目標的影響,并據此提出適用于該模式的啟發式規則;路飛等[8]采用粗糙規劃理論建立調度模型,采用災變型文化算法有效解決了不確定加工時間的工件生產排序問題;金玉蘭等[9]以維修成本、最大完成時間、加權總完工時間、加權總延遲時間為優化目標,提出了多目標遺傳算法;陶辛陽等[10]通過決策最小作業中斷成本、最小最大期望延期成本、最小總期望延期時間三個目標實現全局優化;王世進[11]以總計作業加權完成時間和總計維護成本最小為優化目標,提出改進的蟻群算法求解。此外,王世進[12]在多目標優化的基礎上,進一步提出了基于Lorenz非劣關系的改進NSGA-Ⅱ算法。
上述研究通過多目標決策對生產調度和預防性維護進行聯合優化,并取得了較好的效果,但都是僅僅通過優化工件生產排序方案的方式來進行調度決策,卻忽視了影響決策優劣的生產批量這一關鍵因素。生產調度中的工件加工順序方案和批量決策都對調度結果起到關鍵性的作用,本文旨在建立一個綜合決策工件集批量和生產順序的生產調度和預防性維護集成優化模型,并首次提出了適合該集成模型的變長度染色體基因結構及其遺傳方式,同時,考慮到鑒于NSGA-Ⅱ易產生早熟的缺陷,進一步引入災變機制克服算法過早收斂的缺陷。
1 問題描述和模型建立
以單機系統為研究對象,假設該調度期內訂購m個不同類型產品的z個訂單,可分為n個以1 000件為單位的工件集,工件集不允許中斷,假定所有工件集運輸時間為零。
令xij為0/ 1變量,如果工件集j在第i個位置加工,則xij=1,否則xij=0。據此定義三維向量Ji表示第i個位置加工的工件情況,Ji包括三個特征變量:ai為實數變量,表示該工件集加工的產品類型;bi為實數變量,決定該工件集的加工數量;pi為0/ 1變量,如果在加工第i個位置工件之前進行預防性維護,則pi=1,否則pi=0。
本文其他變量的定義如下:i為工件集的編號,i=1,2,…,n,其中n是工件集的數量;d為工件類型的編號,d=1,2,…,m,其中m是工件類型的數量;k為訂單的編號,k=1,2,…,z,其中z是該調度期內訂單的數量;tp為系統預防性維護時間;cp為系統預防性維護成本;tr為系統平均故障維修時間;cr為系統平均故障維修成本;Ni為加工工件集Ji期間機器故障次數的統計變量;t[i][j]為換模時間矩陣,表示從工件類型i變換至工件類型j所需的換模時間;e[i]為機器在加工工件集Ji之前的機器役齡;f[i]為機器在加工工件集Ji之后的機器役齡;c[d]為d類型產品的單位制造成本耗費;t[d]為d類型產品的單位制造時間;S[i]為工件集Ji所花費的庫存成本;L[k],訂單k所需支付的延期成本。
1)機器故障模型。
機器在運行時會發生故障,機器故障會占用機器生產可用時間,降低生產效率。設λ(t)為故障率函數,β和η為二參數威布爾分布的尺寸參數和比例參數,則機器在t時刻時的可靠性為R(t)=e-(t/η)β。考慮到該機器失效形式屬于制造過程的失效,取1.0<β<4.0。可見隨著機器役齡的增加,機器的可靠率降低,發生故障的概率增大。假設進行預防性維護可以使設備“恢復如新”,則適時進行預防性維護會提高機器穩定性;然而即使進行預防性維護仍不能保證在生產過程中不會發生故障,當故障發生時采取應急維修,即僅恢復機器的使用功能而不改變其役齡。由于故障維修不改變機器役齡,故兩次預防性維修間的故障發生的隨機過程符合非齊次泊松分布,在(t1,t2)間的故障期望發生次數為:

對于工件集Ji,其加工期間的期望故障發生次數為:
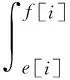
加工該工件之前的機器役齡為:
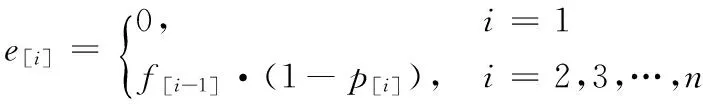
加工之后的機器役齡為f[i]=e[i]+t[ai]·b[i]。
2)懲罰性的預防性維護時間。
當生產任務要求繁多的時候,生產計劃往往存在為了趕工期而忽略預防性維護的傾向,從而導致更高頻率的設備故障和機器使用壽命下降的問題。一般設備運行時間越長,所需的預防性維護時間也會增加,令預防性維護時間呈階段性增加,其具體函數定義如下:
cp=C·tp,C為單位預防性維護時間的維修成本。系統平均故障維修時間tr、成本cr取固定值。
3)安裝/更換模具時間。
在多品種生產任務中,即使機器具有通用性,但不同類型的產品需要不同的模具輔助生產,安裝或更換模具需要占用機器可用時間,時間占用矩陣如下:
其中:tij表示由i類型產品更換至j類型產品時所需的模具更換時間,原則上,tij≠tji,t0j表示生產的第一類產品為j時所需的安裝時間。安裝或更換模具時可同時進行預防性維護。設V[i]表示在加工工件集Ji時是否需要更換模具:需要更換則V[i]=1;否則V[i]=0。
4)存儲/延期成本。
對于某個訂單,若其過早地被生產,則會導致資金機會成本損失和倉儲費用;但若延期交貨,則會導致合同違約懲罰和失去顧客信任等費用。合理地安排生產任務,及時生產及時完工會帶給企業額外的經濟效益。丁佩雯等[13]提出的拖期懲罰隸屬度函數合理地量化了不同程度的拖期完工帶來的懲罰損失,具體如下:
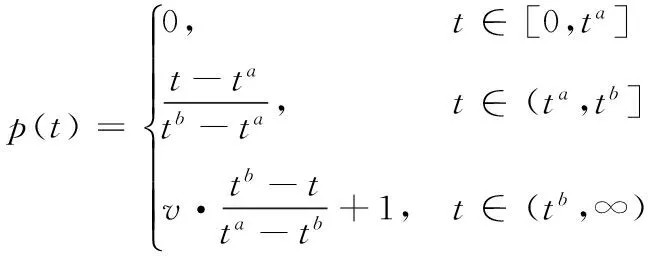
其中v為拖期加速因子。
對于某個訂單O[k],其有3個屬性:產品類型m[k],訂貨數量l[k],交貨期d[k]。設該訂單共被分為e個工件集,則對于某個工件集iko,其所屬訂單的最后一個工件集為ike,該工件集的庫存成本S[iko]=(f[ike]-f[iko])·b[iko]·c[aiko]·R,其中R為單位時間庫存費用率,取0.000 5。而對于該訂單O[k],其延期成本為:
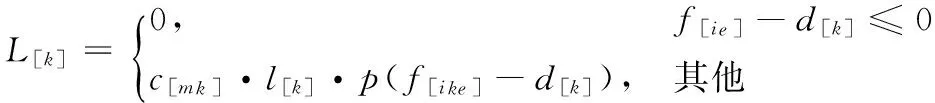
5)目標函數。
總加工時間F1最短化:
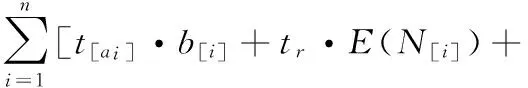
Max(tp·p[i],V[i]·t[i-1][i])]
總制造成本F2最小化:
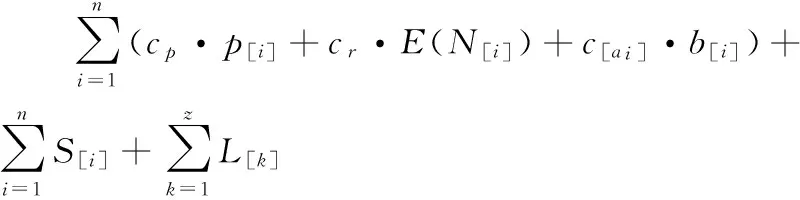
該模型包含以下約束:
(1)
(2)
ai∈{x|1≤x≤m};i=1,2,…,n
(3)
bi≥1;i=1,2,…,n
(4)
(5)
式(1)表示一個工件集只能在一個位置被加工;式(2)表示一個位置只能包含一個工件集;式(3)保證了工件集生產的產品種類是在訂單要求范圍內的;式(4)保證了每個工件集都有實際的意義,不是一個批量為0的假工件集;式(5)表示生產任務符合訂單需求,保證在調度期內足額生產。
2 災變型NSGA-Ⅱ算法設計
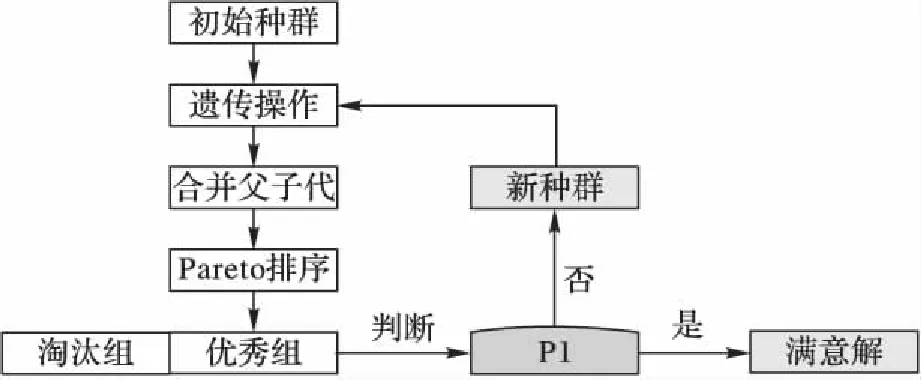
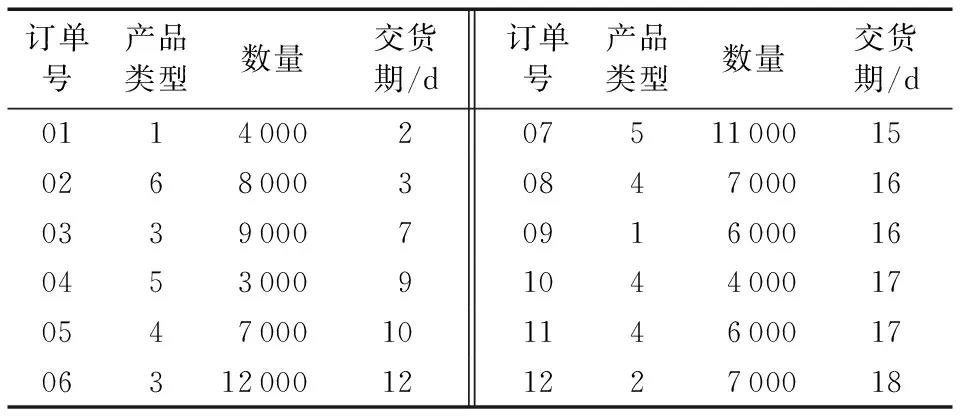
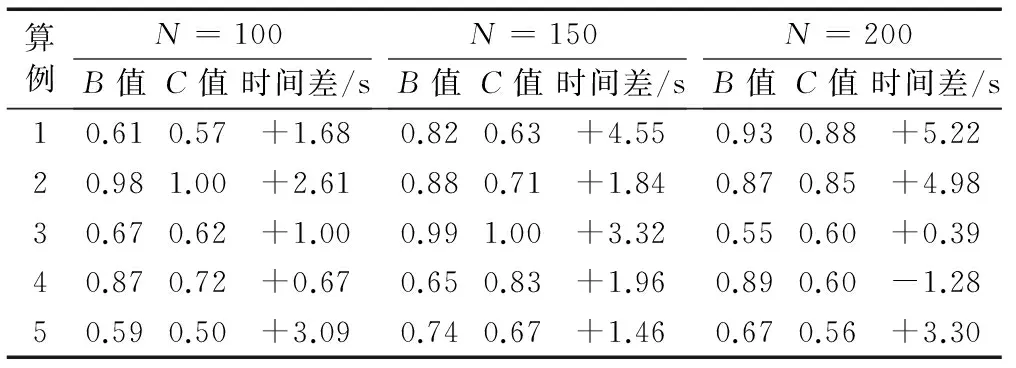
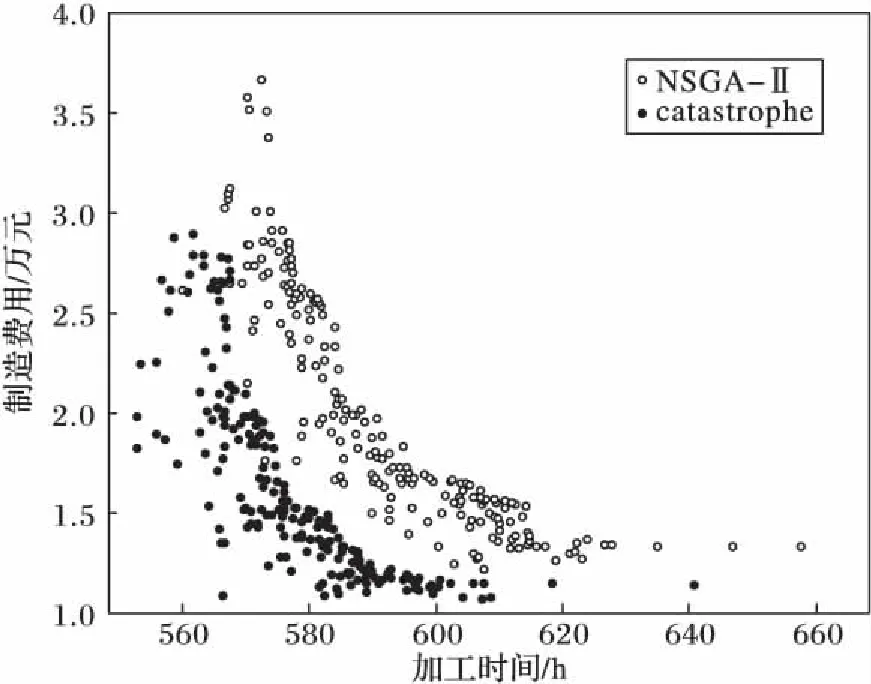
考慮到本文綜合優化制造成本和加工時間兩個指標,故采用由Deb等[14]提出的改進非支配排序方法作為評價種群個體優劣的工具。對于有目標集w的模型求最小值的最優化問題,若滿足?i∈w,fi(x1)≤fi(x2);?i∈w,fi(x1) 1)編碼。 為了不以訂單為單位進行生產調度,優化排產結果,設計如下的編碼以靈活地安排生產種類和數量:K代表產品種類,N代表該工件集的數量,這兩個變量采用實值編碼;P代表是否進行預防性維護,為0/1變量,故采用二進制編碼,若P=1,則代表在加工該工件集之前需要進行預防性維護操作。圖1染色體編碼表示依次生產2類產品3 000件,1類產品7 000件,6類產品2 000件,2類產品5 000件,其中,在生產第2批和第4批工件集之前要對機器進行預防性維護。 圖1 染色體編碼示意圖 Fig. 1 Sample encoding of chromosomes 2)初始解生成。 種群數目N是影響算法運行速度和效率的關鍵因素之一,一般采用20~200或者兩倍的基因位數,在本文算法中染色體因為數目被納入決策變量,故其長度不定,采用種群數目為固定值N。為保證種群多樣性,初始解隨機生成。 3)遺傳操作。 考慮到采用傳統的交叉過程會導致染色體代表的個體方案不可行,如果在交叉后加入修正操作又會很大程度上破壞父代染色體遺傳下來的基因特征,由遺傳操作變為隨機搜索,因而采用單親遺傳算法來保證解的可行性,同時運用基于變長度染色體的截斷算子和拼接算子,達到遺傳操作的目的。以某個染色體PC為例,具體的算子規則如下: PC:(2,3,0)-(1,7,0)-(6,2,1)-(6,3,0)- (3,4,0)-(4,11,0)-(1,4,1) ①截斷算子。 對某個基因(k,n,p)進行截斷操作時,先隨機生成在1~(n-1)范圍內的截斷數x,則生成兩個子代基因(k,x,p)和(k,n-x,p),p位繼承父代,后將分離出的基因(k,x,p)隨機插入染色體中,原父代基因位(k,n,p)替換成(k,n-x,p),生成子代染色體。n=1時無法進行截斷操作。如對(1,7,0)進行截斷操作,若截斷數k=3,則會概率產生如下子代: NC1:(2,3,0)-(1,4,0)-(6,2,1)-(6,3,0)- (1,3,0)-(3,4,0)-(4,11,0)-(1,4,1) ②拼接算子。 對某個基因(k,n1,p1)進行拼接操作時,隨機選擇染色體中另外一個具有相同產品類型k的基因(k,n2,p2),用基因(k,n1+n2,p2)替換基因(k,n2,p2),并將基因(k,n1,p1)移出。若未找到具有相同產品類型的基因,則無法進行拼接操作。如對(1,7,0)進行拼接操作,則會產生如下子代(此例中情況唯一): NC2:(2,3,0)-(6,2,1)-(6,3,0)-(3,4,0)- (4,11,0)-(1,11,1) ③基本位變異算子。 對于基因(k,n,p)中代表預防性維護點的p位,采取基本位變異,則該基因變為(k,n,1-p)。 4)災變機制及榮譽空間。 改進非支配排序遺傳算法(NSGA-Ⅱ)采用了精英策略和父子代共同競爭策略,使種群的最優值得到了有效的保留,局部搜索能力強,但也產生易于陷入局部最優解的缺陷,為了解決這個問題,增強算法的廣域搜索能力,故提出基于榮譽空間的災變模型。所謂災變,就是殺死當前所有的優秀個體以跳出局部極值,從而讓遠離當前極值的點有充分的進化余地。具體規則如下:在子代產生后將父子代合并并進行Pareto排序,將所得Pareto前沿加入榮譽空間,然后合并榮譽空間中新老成員并進行Pareto排序,取Pareto前沿,以此更新榮譽成員。若所得新榮譽空間中有新成員加入,則說明該次迭代子代中產生了更優異的個體。若持續r代未產生新成員,則視為該種群陷入進化陷阱,需要進行災變。若連續災變u次未產生新成員,則視為該種群已充分進化,此時榮譽空間中成員則為最優解。只要有新成員產生,則災變和停滯計數器清零。 根據算法實現所述,具體算法流程如圖2、圖3所示。 圖2 算法總流程Fig. 2 Flowchart of total algorithm 圖3 P1模塊流程Fig. 3 Flowchart of P1 module 為了驗證所提算法的有效性,現將災變型NSGA-Ⅱ與Deb的標準算法在內存4 GB,主頻1.8 GHz的Inter Core i5的Window 8系統中通過Java平臺進行比較。隨機訂單生成如表1所示。 表1 實驗中使用的隨機訂單Tab. 1 Random orders used in the experiment 各參數服從一定區間的平均分布,具體設置如下:t[i][j]=U(0.2,1.5)、tr=U(1.5,3.5)、cr=U(3,6)、c[d]=U(2,17)、t[d]=U(1,14)、η=U(80,100)、β=U(1,4)、r=U(30,100)、u=U(3,6)。預防性維護成本率C=1.7,截斷概率pc=0.35、拼接概率pj=0.35、變異概率pv=0.01,種群規模N=100,150,200,每種規模設置隨機生成10個算例,則共有30個算例。 為了比較兩種算法的優劣,將兩種算法的種群Q1、Q2合并,生成2N規模的種群Qc,對其進行非支配排序,從中挑選出N個較優異個體組成M。定義B(Q1,M)為種群M個體來自種群Q1的比例,C(Q1,M)為種群M的Pareto前沿中個體來自Q1的比例。前者度量了Q1結果的整體優異程度,后者度量了Q1算法的最優值的優劣。因此,B(Q1,M)和C(Q1,M)大于0.5且越接近1,表明Q1的Pareto前沿較之Q2更好,即Q1更優異。表2為種群規模下隨機5個算例的B值、C值和兩種算法的運行時間差。從表2可以看出每個算例中災變型NSGA-Ⅱ都具有比標準NSGA-Ⅱ更優異的結果,同時運算時間無較大差異。 表2 災變型NSGA-Ⅱ和標準NSGA-Ⅱ的實驗對比Tab. 2 Data comparison between catastrophe NSGA-Ⅱ and standard NSGA-Ⅱ 注:“+”表示災變型NSGA-Ⅱ比標準算法多用的時間。 為了具體對比算法的優劣性,從種群規模N=200的算例中隨機挑選一組生成Pareto前沿點分布圖,從圖4中可以清晰地看出災變型NSGA-Ⅱ算法擁有更優異的前沿分布。 圖4 兩算法Pareto前沿點分布圖Fig. 4 Distribution of two algorithms’Pareto front points 在考慮批量大小的基礎上,本文研究了多品種生產任務下的車間調度和預防性維護集成優化問題。針對該問題的特征,基于NSGA-Ⅱ算法提出一種變長度染色體災變性非支配排序多目標遺傳算法對集成模型進行求解,通過各種規模的數據實驗表明,基于災變和榮譽空間機制的改進算法擁有比標準NSGA-Ⅱ算法更優異的廣域搜索能力和尋優能力。本文采用隨機生成染色體的方式初始化種群,初始解的特征分布對算法能力影響的研究及對最終解魯棒性的探討將是下一步的研究方向。 References) [1] 張會紅, 顧幸生, 汪鵬君. 基于免疫算法的生產調度現狀與展望[J].計算機集成制造系統, 2008, 14(11): 2081-2091. (ZHANG H H, GU X S, WANG P J. Status & outlook of immune-algorithm-based production scheduling[J]. Computer Integrated Manufacturing Systems, 2008, 14(11): 2081-2091.) [2] 何法江, 王明紅, 湯以范. 遺傳算法在車間流水作業調度中的應用[J]. 計算機應用, 2010, 30(S2): 274-276.(HE F J, WANG M H, TANG Y F. Application of flow shop scheduling based on genetic algorithm[J]. Journal of Computer Applications, 2010, 30(S2): 274-276.) [3] 張烈平, 張云生, 楊桂華. 基于粒子群算法的流程工業生產調度研究[J]. 計算機工程及應用, 2012, 48(6): 225-228. (ZHANG L P, ZHANG Y S, YANG G H. Research on production scheduling problems in process industry based on particle swarm optimization algorithm[J]. Computer Engineering and Applications, 2012, 48(6): 225-228.) [4] 黃福令, 高慧敏. 基于文化算法和改進差分進化算法的混合算法[J]. 計算機應用, 2009, 29(5): 1264-1267. (HUANG F L, GAO H M. Hybrid algorithm based on cultural algorithm and modified differential evolution algorithm[J]. Journal of Computer Applications, 2009, 29(5): 1264-1267.) [5] 崔維偉, 陸志強. 潘爾順. 基于多目標優化的生產調度與設備維護集成研究[J]. 計算機集成制造系統, 2014, 20(6): 1398-1404. (CUI W W, LU Z Q, PAN E S. Production scheduling and preventive maintenance integration based on multi-objective optimization[J]. Computer Integrated Manufacturing System, 2014, 20(6): 1398-1404.) [6] 崔維偉, 陸志強. 單機系統的生產調度與預防性維護的集成優化[J]. 上海交通大學學報, 2012, 46(12): 2009-2013. (CUI W W, LU Z Q. Integrating production scheduling and preventive maintenance planning for a single machine[J]. Journal of Shanghai Jiaotong University, 2012, 46(12): 2009-2013.) [7] 吳悅, 汪定偉. 交貨期窗口下帶有附加懲罰的單機提前/拖期調度問題[J]. 控制理論與應用, 2000, 17(1): 9-18. (WU Y, WANG D W. Single machine earliness/tardiness scheduling problem with additional penalties about due window[J]. Control Theory and Applications, 2000, 17(1): 9-18.) [8] 路飛, 顧幸生. 基于災變型文化算法的不確定條件下中間存儲時間有限Flow Shop調度[J]. 華東理工大學學報, 2010, 36(5): 708-716. (LU F, GU X S. Finite intermediate storage flow shop scheduling under uncertainty based on cultural algorithm with catastrophe[J]. Journal of East China University of Science and Technology, 2010, 36(5): 708-716.) [9] 金玉蘭, 蔣祖華. 預防性維修計劃和生產調度的多目標優化[J]. 哈爾濱工程大學學報, 2011, 32(9): 1205-1209. (JIN Y L, JIANG Z H. Multi-objective optimization research on preventive maintenance planning and production scheduling[J]. Journal of Harbin Engineering University, 2011, 32(9): 1205-1209.) [10] 陶辛陽, 夏唐斌, 奚立峰. 基于健康指數的預防性維護與多目標生產調度聯合優化建模[J]. 上海交通大學學報, 2014, 48(8): 1171-1174. (TAO X Y, XIA T B, XI L F. Health-index based joint optimization of preventive maintenance and multi-attribute production scheduling[J]. Journal of Shanghai Jiaotong University, 2014, 48(8): 1171-1174.) [11] 王世進. 集成預防性維護計劃的單機調度蟻群優化研究[J]. 工業工程與管理, 2011, 16(6): 60-65. (WANG S J. Ant colony optimization for integrated single-machine production scheduling and preventive maintenance planning[J]. Industrial Engineering and Management, 2011, 16(6): 60-65.) [12] 王世進. 生產調度與維護集成的多目標Lorenz非劣遺傳優化[J]. 工業工程與管理, 2012, 17(2): 1-7. (WANG S J. Multi-objective optimization for integrated production scheduling and maintenance planning with Lorenz non-dominated genetic algorithm[J]. Industrial Engineering and Management, 2012, 17(2): 1-7.) [13] 丁佩雯, 蔣祖華, 胡家文,等. 帶有交貨期時間窗的生產與維護聯合調度優化[J]. 上海交通大學學報, 2015, 49(4): 524-530. (DING P W, JIANG Z H, HU J W, et al. Integrating production scheduling and preventive maintenance for a single machine with due window[J]. Journal of Shanghai Jiaotong University, 2015, 49(4): 524-530.) [14] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. This work is partially supported by the Chinese Postdoctoral Science Foundation (2016M601885), the Natural Science Foundation of Jiangsu Province (BK20141517, BK20150344), the Research Fund Program of Guangdong Provincial Key Laboratory of Computer Integrated Manufacturing (CIMSOF2016005), the Undergraduate Innovational and Entrepreneurship Experimentation Program of Soochow University (2016xj042). WUQingsong, born in 1995. His research interests include intelligent optimization algorithm. YANGHongbing, born in 1977, Ph. D., associate professor. His research interests include machine learning, intelligent information processing. FANGJia, born in 1996. Her research interests include machine learning, intelligent algorithm. Productionschedulingandpreventivemaintenanceintegratedoptimizationbasedoncatastrophemechanism WU Qingsong, YANG Hongbing*, FANG Jia (SchoolofMechanicalandElectricEngineering,SoochowUniversity,SuzhouJiangsu215000,China) On the purpose of integrated optimization of production scheduling and preventive maintenance for multi-product tasks which in producing workshops, an integrated optimization model of production scheduling and preventive maintenance was established comprehensively, in which processing sequence, batch quantity, preventive maintenance measures and other factors were taken into account consequently, on the premise that there are sufficient orders, as well as the joint optimization objective to minimize overall manufacturing costs and processing time. In view of the characteristics of the model, based on the non-dominated sorting genetic algorithm, a single-parent genetic algorithm with variable-length genome was put forward as the resolving method for the model based on the catastrophe mechanism and glory space, which keeps in combination with introducing interruption and splice operators. Besides, under different parameter conditions and various scales of problems, simulative experiments were conducted to verify the efficiency of the proposed algorithm to resolve complex integrated optimization problems of production scheduling and preventive maintenance. length-changeable chromosome; catastrophe; production scheduling; preventive maintenance 2017- 05- 07; 2017- 06- 20。 中國博士后科學基金資助項目(2016M601885);江蘇省自然科學基金資助項目(BK20141517,BK20150344);廣東省計算機集成制造重點實驗室開放基金資助項目(CIMSOF2016005);蘇州大學大學生創新創業訓練計劃(2016xj042)。 吳青松(1995—),男,江蘇常州人,主要研究方向:智能優化算法; 楊宏兵(1977—),男,安徽蕪湖人,副教授,博士,主要研究方向:機器學習、智能信息處理; 方佳(1996—),女,江蘇常州人,主要研究方向:機器學習、智能算法。 1001- 9081(2017)11- 3330- 05 10.11772/j.issn.1001- 9081.2017.11.3330 (*通信作者電子郵箱yanghongbing@suda.edu.cn) TP312 A2.1 算法實現
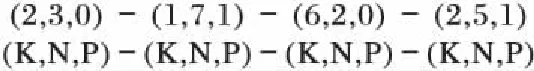
2.2 算法流程

3 算例分析
4 結語

