慣性/地磁組合導(dǎo)航智能分段融合方法

丁柏超，全 偉，楊 旭

(北京航空航天大學(xué) 儀器科學(xué)與光電工程學(xué)院，北京 100191)

慣性/地磁組合導(dǎo)航智能分段融合方法

丁柏超，全 偉，楊 旭

(北京航空航天大學(xué) 儀器科學(xué)與光電工程學(xué)院，北京 100191)

為了減少磁傳感器數(shù)據(jù)異常導(dǎo)致的慣性/地磁組合系統(tǒng)的定位誤差，提出基于χ2狀態(tài)檢驗法的慣性/地磁組合導(dǎo)航智能分段融合方法：利用χ2狀態(tài)檢驗法來檢測組合濾波器的狀態(tài)；通過量測狀態(tài)和系統(tǒng)估計狀態(tài)之間的差異來判斷磁信號是否異常；根據(jù)判斷結(jié)果對慣性/地磁數(shù)據(jù)進行分段融合。在數(shù)據(jù)異常階段，若磁數(shù)據(jù)可用則調(diào)整組合濾波系數(shù)來抑制組合系統(tǒng)誤差，若磁數(shù)據(jù)不可用則直接單獨進行慣導(dǎo)解算，從而實現(xiàn)慣性/地磁組合導(dǎo)航智能分段融合。仿真結(jié)果表明，所提出的方法能有效抑制磁數(shù)據(jù)異常引起的定位誤差。

組合導(dǎo)航；慣性導(dǎo)航；地磁導(dǎo)航；χ2狀態(tài)檢驗；數(shù)據(jù)融合

0 引言

慣性導(dǎo)航系統(tǒng)是一種具有戰(zhàn)略意義的自主導(dǎo)航定位系統(tǒng)，同時也是目前我國遠程戰(zhàn)略武器中的主要導(dǎo)航手段[1]；但慣性導(dǎo)航系統(tǒng)的導(dǎo)航誤差隨時間不斷積累，長時間應(yīng)用情況下其定位誤差很大，不能滿足實用情況下對精度的需求。與其他導(dǎo)航定位系統(tǒng)組合進行應(yīng)用是抑制慣性導(dǎo)航系統(tǒng)誤差發(fā)散的一種常用有效手段[2-3]。地磁匹配導(dǎo)航也屬于自主導(dǎo)航，具有體積小、成本低、隱蔽性強的特點[4-5]，尤其在跨海、跨平原、水下等應(yīng)用環(huán)境下是很高效的導(dǎo)航定位方式之一[6-7]。因此，研究高性能、低成本、全天時、全天候的地磁/慣性組合導(dǎo)航對載體自主導(dǎo)航定位具有十分重大的戰(zhàn)略意義[8-10]。地磁/慣性組合導(dǎo)航技術(shù)已經(jīng)在美國、瑞典、俄羅斯、法國等國家得到發(fā)展與應(yīng)用。自從美國波音公司將地磁輔助導(dǎo)航系統(tǒng)應(yīng)用于飛機后，地磁導(dǎo)航技術(shù)在航天航空導(dǎo)航領(lǐng)域得到快速發(fā)展。其中：英國的西爾索研究所(Silsoe Research Institute)[11]、美國的佛羅里達大西洋大學(xué)(Florida Atlantic University)[12]等研究部門開展了慣性導(dǎo)航信息和地磁數(shù)據(jù)組合技術(shù)研究；國內(nèi)北京航空航天大學(xué)、國防科學(xué)技術(shù)大學(xué)、航天三院等單位也開展了慣性/地磁組合導(dǎo)航定位相關(guān)技術(shù)研究[13-17]。其中北京航空航天大學(xué)“十五”期間，在國家“863計劃”支持下開展了地磁測量、地磁圖建立、地磁圖匹配定位和慣性/地磁組合導(dǎo)航等方面的理論研究與相關(guān)實驗驗證工作。目前，進一步深入開展原子磁強計研制工作，且已經(jīng)取得了一定的進展。下一步擬將原子磁強計應(yīng)用于慣性/地磁組合導(dǎo)航定位系統(tǒng)中。磁傳感器測量信號易受環(huán)境干擾導(dǎo)致地磁匹配定位誤差增大、影響組合導(dǎo)航系統(tǒng)精度。除了磁傳感器方面誤差外，運載體本身和周圍環(huán)境也會產(chǎn)生磁場干擾，影響慣性/地磁組合導(dǎo)航系統(tǒng)性能，并將限制慣性/地磁組合導(dǎo)航系統(tǒng)的廣泛應(yīng)用。這是目前慣性/地磁組合導(dǎo)航系統(tǒng)中需要解決的一個重大問題。

本文針對慣性/地磁組合導(dǎo)航系統(tǒng)特點，分析磁信號誤差對組合系統(tǒng)性能的影響，研究基于χ2狀態(tài)檢驗法的慣性/地磁組合導(dǎo)航智能分段融合方法。

1 慣性/地磁組合導(dǎo)航

慣性/地磁組合導(dǎo)航是一種全自主的遠程、高精度導(dǎo)航方案。此方案中融合了慣性導(dǎo)航系統(tǒng)短時精度高、數(shù)據(jù)連續(xù)平滑和地磁匹配定位系統(tǒng)誤差隨機波動、但不隨時間發(fā)散的特點，通過將2個系統(tǒng)輸出數(shù)據(jù)進行融合，實現(xiàn)遠程、長時間的高精度、自主導(dǎo)航定位。慣性/地磁組合導(dǎo)航系統(tǒng)以慣性導(dǎo)航系統(tǒng)誤差方程為系統(tǒng)模型、以地磁匹配定位結(jié)果為外部位置量測，利用卡爾曼濾波進行信息融合，其融合方案如圖1所示。

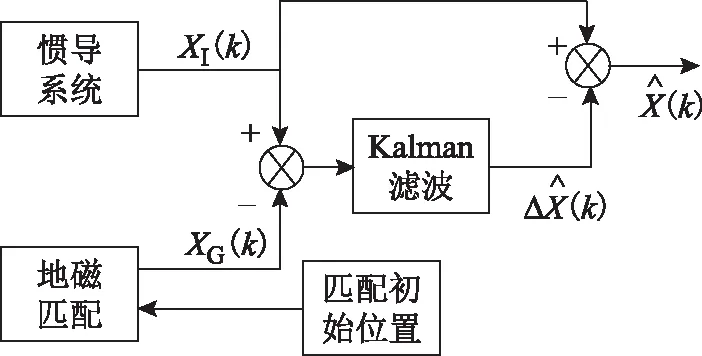
圖1 組合方案原理

考慮姿態(tài)誤差、速度誤差、位置誤差、陀螺漂移和加速度計偏置，所選的13維狀態(tài)量為

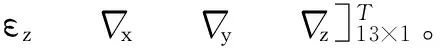
(1)

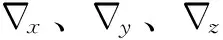
離散化的卡爾曼濾波方程為

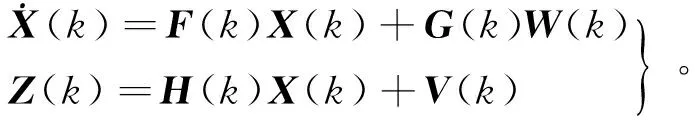
(2)

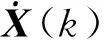
傳統(tǒng)慣性/地磁組合導(dǎo)航中需要陀螺儀、加速度計和地磁定位的統(tǒng)計誤差值，做為Kalman濾波中狀態(tài)估計與增益系數(shù)調(diào)整的依據(jù)。如果在系統(tǒng)運行過程中陀螺儀、加速度計和地磁定位誤差的統(tǒng)計特性發(fā)生變化，則濾波參數(shù)不能正確計算，導(dǎo)致組合導(dǎo)航系統(tǒng)出現(xiàn)定位誤差；因此通過對Kalman濾波狀態(tài)量的監(jiān)測判斷各子系統(tǒng)的運行狀態(tài)，并采取相應(yīng)的方法來抑制子系統(tǒng)故障導(dǎo)致的組合導(dǎo)航誤差，是一種低成本的有效方法。

2 χ2狀態(tài)檢驗方法

χ2檢驗法可實時地確定系統(tǒng)測量信息的有效性[18]，因而十分適用于子系統(tǒng)級的故障檢測/隔離。χ2檢驗法是一種通過檢驗所構(gòu)造的n維高斯分布隨機向量的均值和方差是否與假設(shè)值相符而判斷是否發(fā)生故障的統(tǒng)計假設(shè)檢驗法[19]。根據(jù)所構(gòu)造的隨機向量不同而有不同的檢驗法，其故障檢測性能也有所不同。

(3)

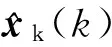
設(shè)檢測函數(shù)為

λβ(k)=βT(k)T-1(k)β(k)。

(4)

無故障時為

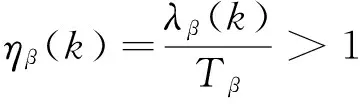
(5)

有故障時為

(6)

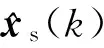
3 仿真實驗與結(jié)果分析

3.1 分段融合方案

基于以上的基本原理與方法，本文進行了慣性/地磁組合導(dǎo)航智能分段融合方法的仿真實驗：基于χ2狀態(tài)檢驗方法，對慣性/地磁組合導(dǎo)航系統(tǒng)中地磁信號出現(xiàn)異常的情況進行判斷；并依據(jù)判斷結(jié)果，對慣性/地磁數(shù)據(jù)進行分段融合。分段融合方案如圖2所示，通過χ2狀態(tài)檢驗方法檢測出磁數(shù)據(jù)異常與否。

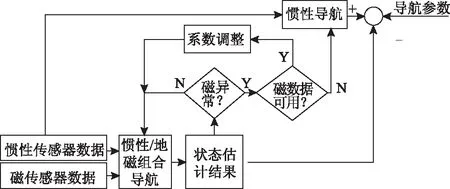
圖2 慣性/地磁組合導(dǎo)航智能分段融合方案

圖中可見：如果磁數(shù)據(jù)正常，則在正常階段運行慣性/地磁組合導(dǎo)航算法；而磁數(shù)據(jù)異常時，如果磁誤差的隨機誤差特性在合理范圍內(nèi)發(fā)生變化，則可以通過實時調(diào)整Kalman濾波方程中量測誤差的系數(shù)來抑制組合系統(tǒng)誤差，如果磁數(shù)據(jù)異常、不可用，則在異常階段運行慣性導(dǎo)航算法。此方案可避免地磁信號異常時間過長導(dǎo)致的組合濾波結(jié)果發(fā)散。

3.2 仿真分析

磁數(shù)據(jù)異常可分為2種情況：一是磁傳感器輸出信號誤差；二是磁場模型誤差。此部分仿真暫不考慮磁場模型誤差，只根據(jù)原子磁強計的精度來確定磁定位誤差，并將此誤差應(yīng)用于慣性/地磁組合導(dǎo)航，對慣性/地磁組合導(dǎo)航誤差特性進行分析，以驗證本項目提出的基于χ2狀態(tài)檢驗的智能分段融合方法。由于實驗設(shè)施和實驗環(huán)境、費用、耗時等條件的限制，為能在較短時間內(nèi)對所提出的方法進行驗證，并滿足具有較高的可信度和逼真度的要求，最終選擇進行半物理仿真。

半物理仿真又稱半實物仿真，是指針對研究內(nèi)容，將被仿真對象系統(tǒng)的一部分以實物方式引入仿真回路。與計算機仿真相比，半物理仿真結(jié)果具有較高的可信度；而與實際實驗相比，又大大節(jié)省人力、時間、資金，所以常用來驗證系統(tǒng)方案的正確性和可行性[21]。

仿真研究的具體思路如下：

1)用軌跡發(fā)生器產(chǎn)生一水下運動軌跡(包括運動軌跡上的全部導(dǎo)航參數(shù))。

2)在軌跡發(fā)生器產(chǎn)生的傳感器數(shù)據(jù)真值上疊加傳感器噪聲數(shù)據(jù)。在此運動過程中有一段時間的磁傳感器輸出信號異常。磁傳感器數(shù)據(jù)應(yīng)用半物理方法產(chǎn)生。半物理數(shù)據(jù)產(chǎn)生方法為：采集真實傳感器的輸出數(shù)據(jù)，求均方差并去掉平均值；將此數(shù)據(jù)乘以系數(shù)得到均方差為0.08 nT(對應(yīng)10 m定位誤差)的正常數(shù)據(jù)和均方差為0.8 nT(對應(yīng)100 m定位誤差)的數(shù)據(jù)；把此數(shù)據(jù)疊加到軌跡發(fā)生器產(chǎn)生的定位數(shù)據(jù)上形成具有真實誤差特性的實驗數(shù)據(jù)。陀螺、加速度計的誤差數(shù)據(jù)也是采用此方法生成。

3)分別利用本項目提出的基于χ2狀態(tài)檢驗的智能分段融合方法和傳統(tǒng)組合方法進行數(shù)據(jù)融合，并對2種組合方法進行對比分析。

規(guī)劃載體運動條件為：起始點緯度40°，經(jīng)度130°，初始高度是水下100 m，初始航向角30°，俯仰角、橫滾角都為0°，載體速度5 m/s，航行時間30 min。航行過程中航向變化10°，水平姿態(tài)和速度不變。其中，在第15到20 min時磁傳感器數(shù)據(jù)異常、誤差很大。慣性導(dǎo)航系統(tǒng)中陀螺儀的漂移為0.01(°)/h，加速度計隨機常值為50 μg。正常情況下應(yīng)用本課題組研制的磁強計能達到的定位精度為10 m；但磁定位異常時位置誤差很大且隨機變化，仿真中設(shè)為正常定位誤差的10倍。對以上所設(shè)的仿真數(shù)據(jù)，分別用傳統(tǒng)Kalman濾波和本文智能分段融合方法進行處理，得到經(jīng)度、緯度、高度誤差如圖3和圖4所示。

圖3 經(jīng)度誤差

圖3及圖4中波動較大的細實線是傳統(tǒng)Kalman濾波處理結(jié)果，趨于平穩(wěn)的粗實線是采用本文方法處理的結(jié)果。由數(shù)據(jù)可見，在900到1 200 s

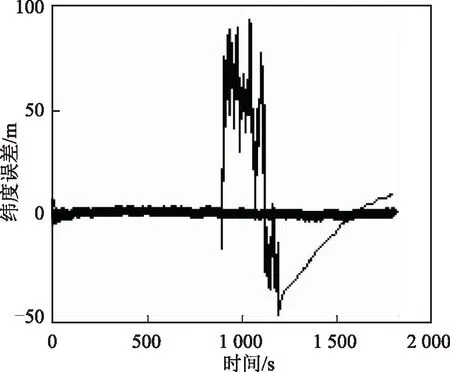
圖4 緯度誤差

(15到20 min)時間內(nèi)由于地磁傳感器數(shù)據(jù)異常導(dǎo)致慣性/地磁組合導(dǎo)航系統(tǒng)定位精度下降，而且當?shù)卮艛?shù)據(jù)正常時濾波精度也受到影響。應(yīng)用χ2狀態(tài)檢驗法檢測出磁信號量測異常后，調(diào)整Kalman濾波器量測量的加權(quán)系數(shù)，使故障信號對系統(tǒng)影響降低；而當磁信號不可用時，進入慣性導(dǎo)航模式，消除磁信息對定位信號的污染。在不同情況采用不同的加權(quán)系數(shù)，分段融合，提高了組合系統(tǒng)的可靠性。可見采用本文方法能有效抑制磁數(shù)據(jù)異常導(dǎo)致的定位誤差。

4 結(jié)束語

針對地磁傳感器信號異常引起組合導(dǎo)航系統(tǒng)出現(xiàn)誤差的問題，在對慣性/地磁組合導(dǎo)航系統(tǒng)特點分析的基礎(chǔ)上，提出基于χ2狀態(tài)檢驗的慣性/地磁組合導(dǎo)航智能分段融合方法，并對該方法進行仿真驗證。實驗結(jié)果證明，本文方法能有效減少磁信號異常引起的定位誤差從而提高組合導(dǎo)航精度。為取得更高的定位精度，接下來還需要在建立高精度3維地磁圖以及地磁圖誤差建模與補償方面展開深入研究。

[1] 李豐陽,賈學(xué)東,董明.慣性/視覺組合導(dǎo)航在不同應(yīng)用場景的發(fā)展[J].導(dǎo)航定位學(xué)報,2016,4(4):31-35.

[2] 楊春雷.無人機捷聯(lián)慣性/全光自主組合導(dǎo)航系統(tǒng)研究[J].四川兵工學(xué)報,2015,36(11):4-7.

[3] LEE I U,LI H,HOANG N M,et al.Navigation system development of the underwater vehicles using the GPS/INS sensor fusion[C]//The Institute of Electrical and Electronic Engineers(IEEE).Proceedings of 2014 14th International Conference on Control,Automation and Systems(ICCAS 2014).Seoul:IEEE,2014:610-612.

[4] TYREN C.Magnetic anomalies as a reference for ground—speed and map-matching navigation[J].Journal of Navigation,1982,35(2):242-254.

[5] TYREN C.Magnetic terrain navigation[C]//The Institute of Electrical and Electronic Engineers(IEEE).Proceedings of the 1987 5th International Symposium on Unmanned Untethered Submersible Technology.Sweden:IEEE,1987:245-256.

[6] ZHANG Y S,LI C Y,LIU S S,et al.Locating method of geomagnetic/inertial integrated navigation system by forecasting the geomagnetic matching initial value[C]//The Institute of Electrical and Electronic Engineers(IEEE).Proceedings of 2014 IEEE Chinese Guidance,Navigation and Control Conference.Yantai:IEEE,2014:235-239.

[7] LUO H,DENG Z,FU M,et al.A map matching algorithm for inertial navigation systems based on the adaptive projection method[C]//The Institute of Electrical and Electronic Engineers(IEEE).Proceedings of International Symposium on Computational Intelligence and Design.Hangzhou:IEEE,2015:304-308.

[8] THIENEL J,HARMAN R,BARITZHACK I,et al.Results of the magnetometer navigation(MAGNAV) inflight experiment[J].Experimental Brain Research,2006,116(1):97-103.

[9] 郭才發(fā),胡正東,張士峰,等.地磁導(dǎo)航綜述[J].宇航學(xué)報,2009,30(4):1314-1319.

[10] KAMGAR-PARSI B,KAMGAR-PARSI B.Vehicle localization on gravity maps[C]//International Society for Optical Engineering(SPIE).Proceedings of SPIE 3693.Florida:SPIE,1999:182-191.doi:10.1117/12.354447.

[11] SMITH R,FROST A,PROBERT P.Aspects of heading determination via fusion of inclinometer and magnetometer data[C]//The Institute of Electrical and Electronic Engineers(IEEE).Proceedings of the 8th International Conference on Advanced Robotics(ICAR '97).Monterey:IEEE,1997:739-744.

[12] GRENON G,AN P E,SMITH S M,et al.Enhancement of the inertial navigation system for the morpheus autonomous underwater vehicles[J].IEEE Journal of Oceanic Engineering,2001,26(4):548-560.

[13] 劉穎,吳美平,胡小平,等.基于等值線約束的地磁導(dǎo)航匹配方法[J].空間科學(xué)學(xué)報,2007,27(6):505-511.

[14] 任治新,羅詩途,吳美平,等.基于改進ICP算法的地磁圖匹配技術(shù)[J].計算機技術(shù),2008(28):351-354.

[15] 李素敏,張萬清.地磁場資源在匹配制導(dǎo)中的應(yīng)用研究[J].制導(dǎo)與引信,2004,25(3):19-21.

[16] 吳美平,劉穎,胡小平.ICP算法在地磁輔助導(dǎo)航中的應(yīng)用[J].航天控制,2007,25(6):17-21.

[17] 王可東,陳偲.水下地形匹配等值線算法研究[J].宇航學(xué)報,2006,27(5): 995-999.

[18] DRAGANOV S.Detection of biases and faults in navigation sensor measurements[C]//The Institute of Electrical and Electronic Engineers(IEEE).Proceedings of 2016 IEEE/ION Position,Location and Navigation Symposium(PLANS).Savannah GA:IEEE,2016:1008-1014.

[19] YUN S H,KANG C W,PARK C G.Reducing the computation time in the state chi-square test for IMU fault detection[C]//The Institute of Electrical and Electronic Engineers(IEEE).Proceedings of the 14th International Conference on Control,Automation and Systems(ICCAS 2014).Seoul:IEEE,2014:879-883.

[20] 郭鵬,張濤,程農(nóng).組合導(dǎo)航系統(tǒng)故障診斷方法設(shè)計與實現(xiàn)[J].系統(tǒng)仿真學(xué)報,2010,22(增刊1):224-227.

[21] 吳雙.半物理仿真系統(tǒng)現(xiàn)狀及發(fā)展趨勢[J].工業(yè)儀表與自動化裝置,2016(2):16-20.

Anintelligentpiecewisedatafusionmethodofinertial/geomagneticintegratednavigation

DINGBaichao，QUANWei，YANGXu

(School of Instrumentation and Optoelectronic Engineering，Beihang University，Beijing 100191，China)

In order to reduce the positioning errors caused by the abnormal data of the magnetic sensor in inertial/geomagnetic integrated navigation system，the paper proposed an intelligent piecewise data fusion method of inertial/geomagnetic integrated navigation based onχ2state verification：χ2state verification was used to detect the state of filter； and the signal abnormality of the magnetic sensor was judged through the difference between the measurement state and the estimation state； the piecewise data fusion was implemented according to the judging results finally.In the stage of data abnormal，if the magnetic data is available，the errors of system could be suppressed after adjusting the integrated filtering coefficients； if not available，the inertial navigation resolution would be carried out directly.By this way，the intelligent piecewise data fusion method of inertial/geomagnetic integrated navigation could be realized.Simulation result showed that the proposed method could reduce the positioning errors caused by the abnormal data of the magnetic sensor effectively.

integrated navigation； inertial navigation； geomagnetic navigation；χ2state verification； data fusion

2016-11-23

國家自然科學(xué)基金項目(61374210，61473019，51574012)；天津市智能遙感信息處理技術(shù)企業(yè)重點實驗室開放基金項目(2016-ZW-KFJJ-01)。

丁柏超(1994—)，女，黑龍江佳木斯人，碩士研究生，研究方向為慣性技術(shù)與導(dǎo)航。

丁柏超，全偉，楊旭.慣性/地磁組合導(dǎo)航智能分段融合方法[J].導(dǎo)航定位學(xué)報，2017，5(4)：1-5.(DING Baichao，QUAN Wei，YANG Xu.An intelligent piecewise data fusion method of inertial/geomagnetic integrated navigation[J].Journal of Navigation and Positioning，2017，5(4)：1-5)

10.16547/j.cnki.10-1096.20170401.

P228

A

2095-4999(2017)04-0001-05