善用數學模型,秒解中考試題
舒盛花

[摘? 要] 隨著課改的深入,數學更注重抽象思維能力的培養,更貼近解決生活中的實際問題. 平移模型,“K”形模型,將軍飲馬模型等是初中數學解題教學的常見模型,這類數學問題對能力要求較高,需要教師引導學生將所學內容整理歸納出類型和方法,并經過加工提煉和保存.
[關鍵詞] 數學模型;平移模型;K形模型;將軍飲馬模型
平移模型、“K”形模型、將軍飲馬模型是中考的熱點,這類問題既充滿生活的趣味性,又是對數學思維的挑戰,對能力要求較高,需要靈活地運用圖形特點抽象概括出解題方法,并加以應用和拓展,形成解題經驗,我們把這些圖形或數學問題稱為數學模型. 在平時教學中,老師如果善于總結常見的數學模型,會給復習帶來事半功倍的效果. 本文結合筆者平時的教學,談談在初三復習中如何善用數學模型,秒解中考試題.
平移模型
浙教版教材七年級下冊1.5中我們學過了“圖形的平移”,移動的特點是在移動過程中原圖形上所有的點都沿著同一方向移動相等的距離. 利用這一特性,教學時可以把“圖形的平移”轉化為“點”的平移來解決類似平行四邊形的問題.
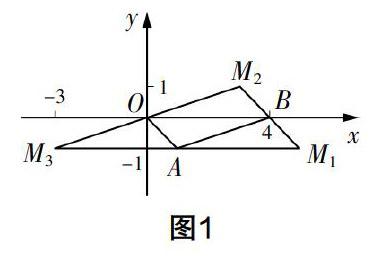
例1 如圖1,在平面直角坐標系中,已知點O(0,0),A(1,-1),B(4,0),點M為坐標平面內一點,若以點O,A,B,M為頂點的四邊形是平行四邊形,則點M的坐標是______.
分析? 由O,A,B,M為頂點的四邊形是平行四邊形,可分2種情況.
解答? (1)以OA為一邊,即OA∥BM,此時,①若點M在點B的下方,則O(0,0)平移到A(1,-1),可知橫坐標增大1,縱坐標減小1,由平行四邊形的性質(對邊平行且相等)可知B(4,0)平移到點M,則其橫坐標增大1,縱坐標減小1,故M1(5,-1);②若點M在點B的上方,則A(1,-1)平移到O(0,0),可知橫坐標減小1,縱坐標增大1,由平行四邊形的性質可知,B(4,0)平移到點M,則其橫坐標減小1,縱坐標增大1,故M2(3,1).
(2)以OA為對角線,則OM∥BA,此時B(4,0)平移到A(1,-1),可知橫坐標減小3,縱坐標減小1. 由平行四邊形的性質可知,O(0,0)平移到點M,則橫坐標減小3,縱坐標減小1,故M3(-3,-1).
點評? 采用了“點的平移”這個模型后,解題快捷方便,在方法上,學生由被動接受變為主動探索,使學生能把以前所學的數學知識有機地結合起來.
“K”形模型
“K”形模型,是常見的“一線三等角”的相似模型(由三個等角的頂點在同一條直線上構成的相似圖形,這個角可以是直角,也可以是銳角或者鈍角). 追溯其根源,可以歸納為三角形基架和矩形基架(如圖2和圖3所示). “K”形模型在中考中出現的頻率相當高.
例2 如圖4,AB=4,射線BM和AB互相垂直,點D是AB上的一個動點,點E在射線BM上, 且BE=1/2BD,作EF⊥DE并截取EF=DE,連接AF并延長交射線BM于點C.? 設BE=x,BC=y,則y關于x的函數解析式是(? ? ? )
A. y=-12x/(x-4)? ? ? ? ? ? ? ?B. y=-2x/(x-1)
C. y=-3x/(x-1)? ? ? ? ? ? ? ? ?D. y=-8x/(x-4)
分析? 過點F作FG⊥BC于點G,則可構成“K”形模型.
點評? 利用“K”形模型,關鍵是如何去構造這個模型,有時是“K”字相似,有時是“K”字全等. 教學中,我們要善于抓住此類問題的基礎知識點和本質規律來提煉歸類成簡單的解題模型.
將軍飲馬模型
傳說古羅馬亞歷山大城有一位精通數學和物理的學者,一天,一位羅馬將軍專程去拜訪他,向他請教一個百思不得其解的問題:將軍每天從軍營B出發,先到河邊飲馬,然后再去河岸同側的A地開會,如圖5所示,應該怎樣走才能使路程最短?
分析 飲水點C是動點,顯然可以用構造對稱點來解決問題. 只需連接A′B,與l的交點C,即為路程最短點.
解答? 作點A關于l的對稱點A′,連接A′B,A′B與l的交點C即為所求點.
評析? 若取l上異于C點的點C′,顯然AC′+BC′>A′B.
將軍飲馬模型的原理:在“圖形的軸對稱”一節中出現,根據兩點之間線段最短的原理求最短距離的一個方法模型. 常用于解決最短路徑問題.
例3 如圖6,MN為⊙O的直徑,A,B是⊙O上的兩點,過A作AC⊥MN于點C,過B作BD⊥MN于點D,P為DC上的任意一點,若MN=20,AC=8,BD=6,則PA+PB的最小值是______.
分析? P為直徑MN上的動點,將直徑MN所在的直線看成是模型中的河流,A點和B點分別看成是山峰A和營地B,構造A或者B關于MN的對稱點即可.
點評? 該題型是“兩定點在直線同側,在直線上找到一點到兩定點距離和最短”這一模型,也就是上文提到的“將軍飲馬”模型的簡單應用.
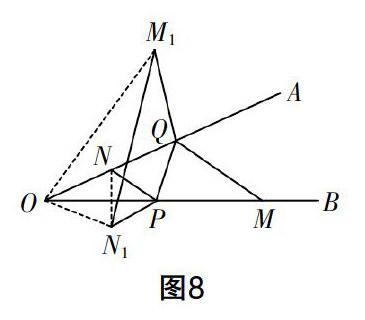
例4 如圖7,∠AOB=30°,點M,N分別在邊OA,OB上,且ON=1,OM=3,點P,Q分別在邊OB,OA上,則NP+PQ+QM的最小值是______.
分析 學生剛接觸到這個題目時,不知道如何去解,因為在他們的印象中,類似將軍飲馬問題都是“已知兩個定點,求一個動點到它們之間的距離和最小”,而此題卻是求兩個動點到已知兩個定點之間的距離和最小,好像無法使用我們熟知的模型了. 此時筆者引導學生,我們可以假設點Q固定,先求解NP+PQ的最小值,這時自然會聯想到利用將軍飲馬的模型作點N關于OB對稱的點N1;接著求解PQ+QM的最小值,同樣可以假設P點固定,也可以利用將軍飲馬的模型作點M關于OA對稱的點M1,分步驟來求解.
點評? 本題滲透了轉化、數學建模等思想,而主導思想在于轉化,通過軸對稱變換把該類問題轉化為利用“兩點之間線段最短”解決的問題,從而達到“化折為直”“化和為一”,將折線、線段的問題歸結為直線問題的目的.
通過以上基本模型,我們發現在平時復習時,要善于提煉數學模型,當遇到數學問題時,首先辨認其屬于哪一類基本模型,再利用模型探索解決問題的策略,這比單純教會學生解題更為重要,意義更加重大.

