基于數據密度感知的非平衡數據模糊聚類方法

王 進，游 磊，黎忠文，苗 放

(1.成都大學 信息科學與工程學院，四川 成都 610106； 2. 成都大學 大數據研究院，四川 成都 610106)

基于數據密度感知的非平衡數據模糊聚類方法

王 進1，游 磊1，黎忠文1，苗 放2

(1.成都大學 信息科學與工程學院，四川 成都 610106； 2. 成都大學 大數據研究院，四川 成都 610106)

非平衡數據分析是數據領域的重要問題之一，其類間分布的巨大差異給聚類方法帶來嚴峻挑戰.圍繞非平衡數據聚類問題，分析了非平衡數據對模糊聚類方法的影響，提出了基于密度感知的模糊聚類方法.方法將數據分布密度特征嵌入模糊聚類初始化過程中，用于定位初始聚類中心點，避免了少數類中心點位置的消失，在此基礎上進一步設計了基于密度的模糊聚類優化更新方法.經數據集分析驗證，本研究方法能夠有效解決非平衡數據分類中少數類消失問題，并且在聚類算法性能上比傳統方法有明顯提高.

模糊聚類；分布密度；非平衡數據

0 引 言

模糊聚類方法(fuzzy C-means，FCM)，是一種典型的非監督學習方法，其在傳統聚類方法的基礎上，模糊聚類方法引入隸屬度概念，刻畫了每個數據個體與不同類的相似性，隸屬度最大的類被視為該數據個體的母類.對數據隸屬度分布的分析，可以得到數據個體的細節特征.然而，如何處理非平衡數據聚類依然是模糊聚類面臨的一個重要問題[1].非平衡數據的主要特征在于不同類的數據量差異巨大，占多數數據量的主要類往往對聚類結果起決定性影響，造成占少數數據量的次要類在聚類結果中逐漸消失.針對該問題，現有研究主要通過聚類權重進行解決，即按照每類所含數據量分配類權重，確保少數類不受多數類影響，例如，csiFCM、ssFCM、FMLE及siibFCM等[2-6].事實上，由于大多數數據是無標記的，聚類初始無法明確得到每類所含數據點數，使得基于權重的方法應用受到一定的限制.數據分布密度是數據集的重要特征，反映了數據的空間幾何結構.在低維場景下，可直接通過數據分布密度獲取數據聚類信息，高密度區域通常代表潛在的聚類(見圖1).基于該思路，本研究通過數據分布的密度特征進行聚類：聚類初始，通過數據密度選擇初始中心點；聚類過程中，采用潛在中心點附近數據點更新聚類中心位置，由此避免少數類消失問題.具體實現時，采用分治思路對模糊聚類算法重新設計，將FCM算法擴展至可并行計算，應用數據分布密度解決非平衡數據聚類問題.

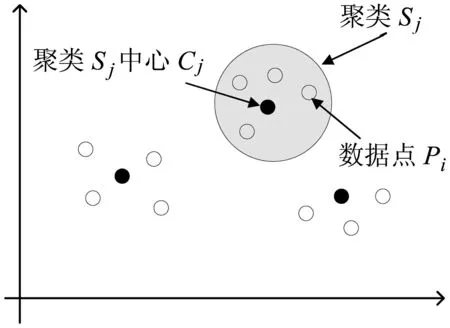
圖1聚類分布示意圖

1 基于密度的模糊聚類算法設計

基于密度的模糊聚類方法，旨在利用數據集的空間幾何結構來優化聚類算法.對此，本研究首先利用高斯核密度估計方法獲取數據的分布密度，將數據集粗分為不同子集，針對不同子集進行局部迭代優化，確保少數類中心點不消失.數據集粗分與子集局部優化是該方法需要解決的2個重要問題.

1.1 基于密度的數據劃分方法設計

通常，聚類中心點鄰域的數據分布密度略高于附近鄰居點的鄰域密度，且距離更高密度點較遠[7].基于該特征，下面給出其具體數學模型，其中包括局部密度和特征距離2個參數.

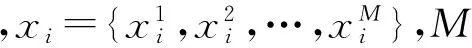
(1)

其中，‖xi-xj‖為歐式距離，dc為距離門限值.

特征距離δi定義為數據點xi到距離其最近的高密度點的距離，如式(2)所示.

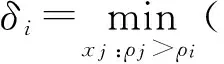
(2)

基于有向無環圖的數據集粗分方法如圖2所示.其中，端點表示數據點，端點之間的有向邊表征其有向鄰居關系，有向邊的長度則為其特征距離.

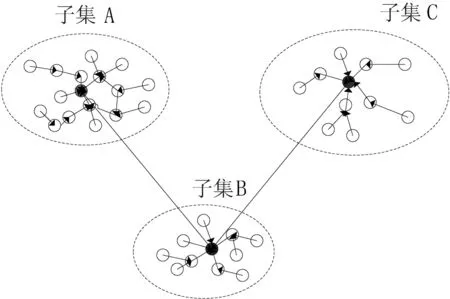
圖2基于有向無環圖的數據集粗分方法

定義1 數據點p的有向鄰居定義為距離該點最近的高密度點，即，

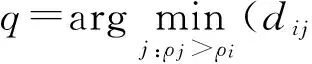
有向鄰居點的若干特性如下：

1)全局密度最高的數據點沒有有向鄰居點，從算法設計角度考慮，將其特征距離設置為，

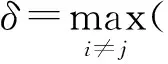
2)有向鄰居點之間密度服從，ρpρq；

3)每個數據點有且僅有一個有向鄰居點；

4)有向鄰居關系是不可逆的，即數據點p的有向鄰居為q，但數據點q的有向鄰居不是p.

由圖2可知，特征距離小的數據點通常跟其有向鄰居位于同一個類中，而特征距離較大的點則與其有向鄰居位于不同類.由此，將有向鄰居圖按照有向邊長度進行粗分為不同區域，即潛在的類.具體分割方法如下：對于任意數據點，如果其特征距離小于門限dc,則將其劃分到與其有向鄰居相同的區域；否則，以該點為中心點構建潛在新類.其類歸并偽代碼如下：

InputtCen={tc1,tc2，…，tck，…，tcM};

Input {tClustk}，k=1,2,…，M;

Input the cluster number C;

tCennew=sortWithGama(tCen,′descending′)

FORj=1:(M-C),

waitForMerge=tCennew[M-j+1];

mergeTo=dirNeighborOf(tCennew[M-j+1]);

tClustmergeTo=Append(tClustwaitForMerge);

END;

由此，將數據集粗分為若干潛在聚類，其中心點具有局部最大的數據密度.本研究將門限dc設置為所有數據距離的2分位點.實際應用中，門限還可以通過優化得到.

依據聚類數量，進一步將上述潛在聚類歸并，并優化數據集分割.假定潛在聚類為，

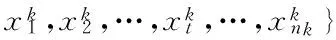
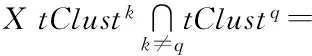
其中，k和nk分別為聚類標識和每個子類tClustk中數據點數量,子類中心點為tCen={tc1,tc2,…，tck，…，tcM}?X.

由于潛在聚類中心點通常同時具有較大特征距離和數據密度[7].基于此，本研究依據γi=δi*σi對所有子類中心進行排序，將所有子類歸并到就近的c個子類中，完成子類歸并.

1.2 子集聚類優化方法

圍繞上述得到的子類，{tClustk}，k=1,2,…，C，進一步設計基于密度的聚類優化方法，

FN×C=[f1，1，f1，2，…，f1，C；…；fN，1，fN，2，…，fN，C]

來表示初始劃分的聚類關系，其中，

本研究進一步將聚類中心點計算方法設計為如式(3)所示，

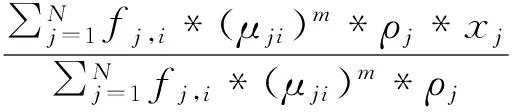
(3)

每次局部中心點位置更新只取決于局部子類中的數據點.模糊聚類的隸屬度和目標函數分別為，

(4)

(5)

基于密度的模糊聚類算法偽代碼如下：

InputtCen={tc1,tc2,…，tck，…，tcM};

Input {tClustk},k=1,2,…，M;

Input the cluster number C,ε;

[tCennew，tClustnew]=Merger(tCen,tClust);

Computed(xi,vj) with Eq. 4;

Compute membership with Eq. 5.

WHILE|Ji+1-Ji|>ε,

Update centroids with Eq. 3;

Computed(xi,vj) with Eq. 4;

Compute membership with Eq. 5.

END;

2 算法性能評估

本研究采用具有代表性的非平衡數據集ecoli-0-1-4-6[9]評估來研究所提算法的性能.數據集ecoli-0-1-4-6包括陽性和陰性2類數據，其中陽性類數據有20例，陰性類數據有260例，數據維度為8.另一個數據集來自文獻[7]，該數據集包括2 535數據樣本，共5類，每個數據樣本維度是2，其每個類所包含的數據量分別為，C1n=1 456,C2n=246,C3n=246,C4n=431,C5n=156.該數據集是無標記的，并且含有噪聲(見圖3).同時，本研究應用文獻[7]方法對數據進行標記，去除部分噪聲.表1詳細給出上述2個數據集的特征信息.

表1 數據集描述

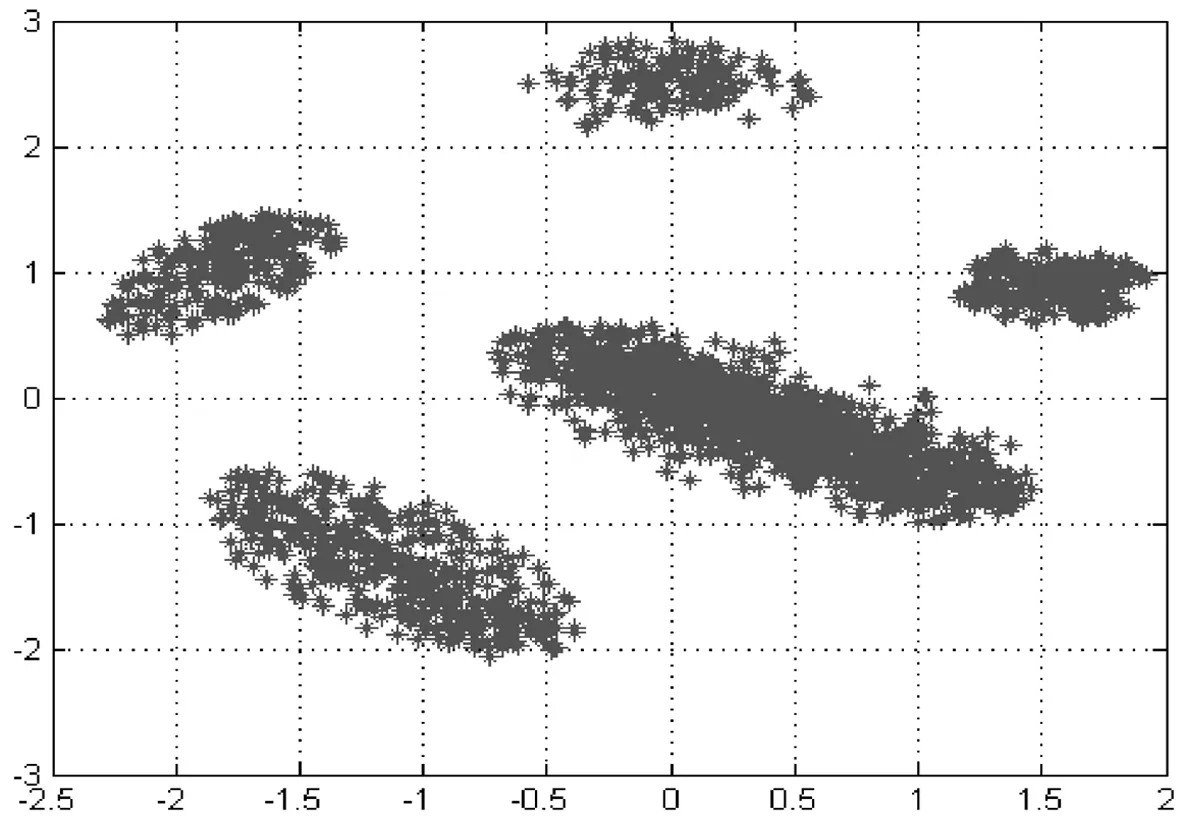
圖3文獻[7]數據集分布

算法性能的比較主要通過聚類準確性與迭代次數來衡量算法在聚類性能和計算性能的差異.

首先，采用文獻[7]數據集分析非平衡數據對聚類性能的影響.該數據集包括2個主要類和3個少數類(見圖3)，其中3個少數類分別與2個主要類極為接近，易受到主類影響.圖4與圖5為采用傳統模糊聚類方法得到的聚類結果.

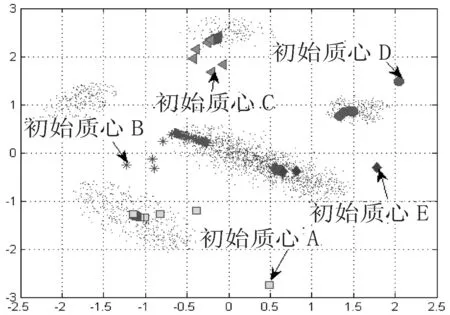
圖4傳統模糊聚類方法的中心點變化

由圖4、圖5可知，其中1個多數類被誤分為2個類.究其原因，傳統聚類算法采用隨機選擇初始中心點，且通常距離真實聚類中心點距離較遠(見圖4)，隨著聚類優化過程不斷進行，聚類中心點逐漸傾向于附近的主要類區域，造成最后沒有聚類中心點落在少數類，尤其初始中心點B，最后漂移到附近的多數類區域.可以看出，傳統模糊聚類方法在處理非平衡數據問題的誤分類率較高.

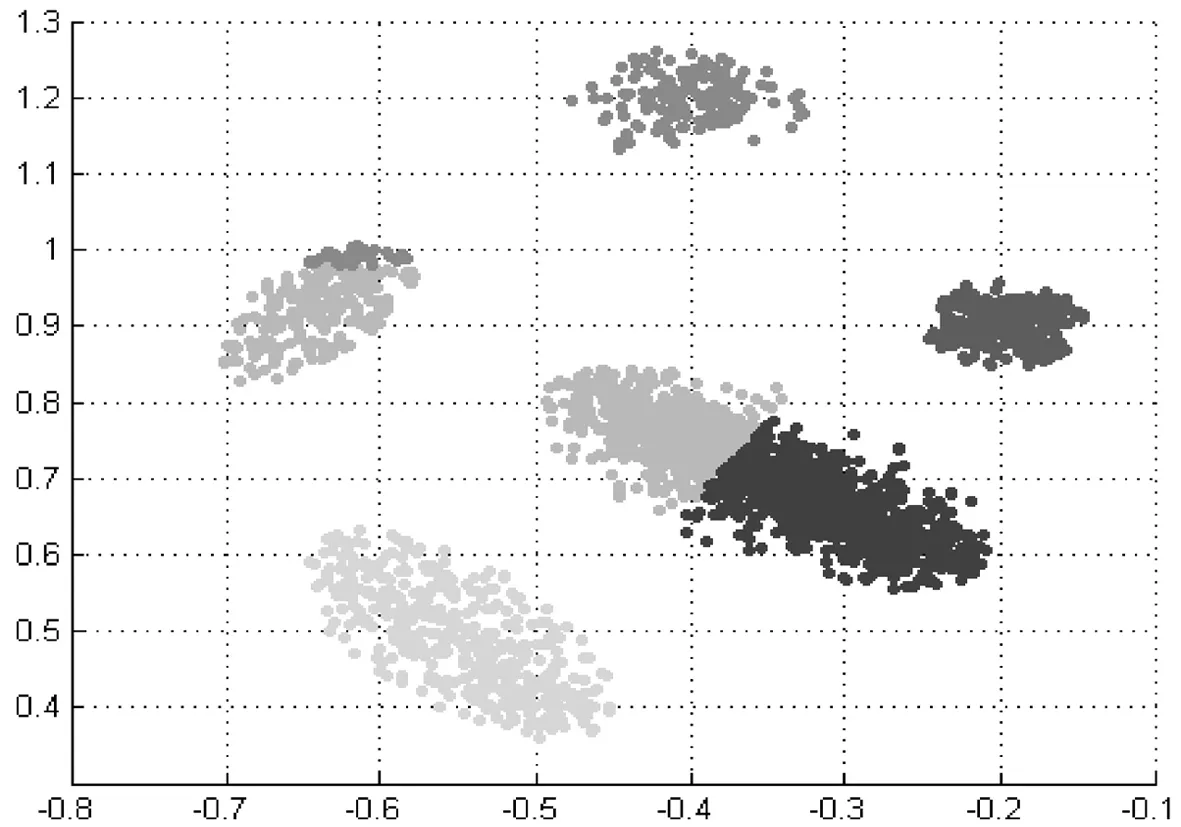
圖5傳統模糊聚類方法在文獻[7]數據集的聚類結果

相比之下，本研究設計的基于密度的聚類方法則始終能保證聚類中心點位于數據分布的高密度區域(見圖6、圖7). 由于本研究采用局部數據密度來優化模糊聚類，使得聚類中心點能夠以較少的迭代次數平穩地收斂.在聚類迭代次數上，本方法僅需要13次聚類迭代，而傳統方法則需要30次；在計算時間上，本方法依然比傳統方法有優勢，具體如表2～表4所示.同時，本研究進一步采用數據集ecoli-0-1-4-6來評估模糊聚類算法和基于密度的模糊聚類算法性能.相比于文獻[7]數據集，數據集ecoli-0-1-4-6空間分布相對較散(見圖8).數據分布密度差異不明顯，可通過此類數據來評估本研究方法在數據空間分布密度差異較小場景下的可用性.由計算結果也可以看出，聚類方法在此類數據集上分類準確性不高.盡管如此，本研究方法依然能夠達到比傳統方法更優的結果(見表3、表4).

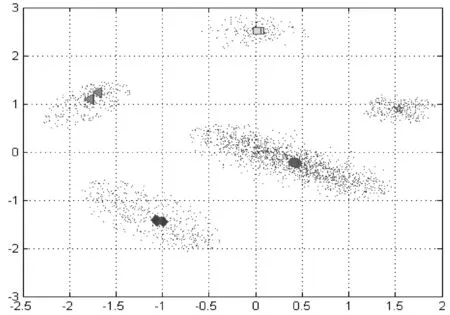
圖6基于密度聚類過程的中心點變化

圖7本研究方法的聚類結果

表2 聚類計算迭代次數評估

表3 計算時間評估

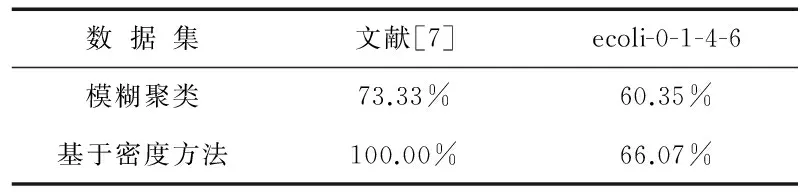
表4 聚類準確性比較

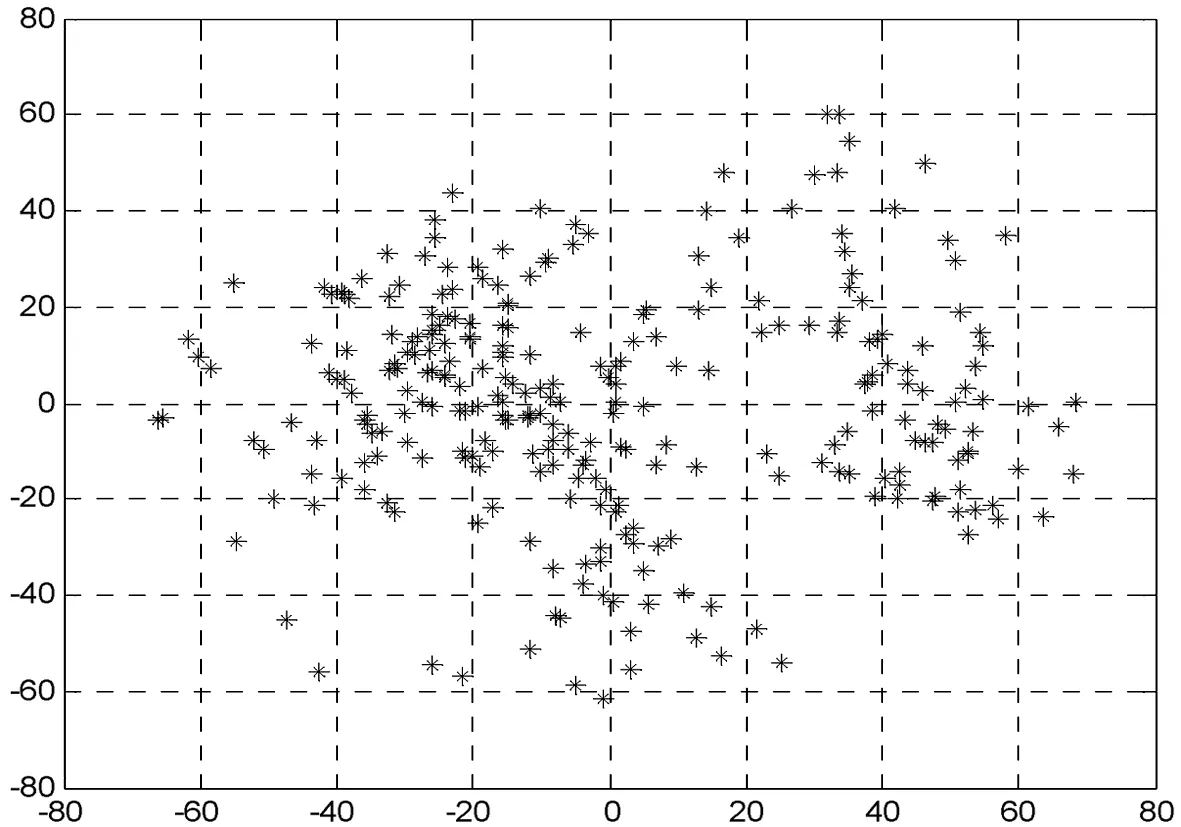
圖8數據集ecoli-0-1-4-6的低維分布

3 結 語

針對非平衡數據聚類少數類消失問題，本研究提出并設計了一種新的模糊聚類算法，該方法采用數據分布密度進行聚類初始點選擇，旨在解決非平衡數據分布造成聚類準確率低的問題.同時，本研究進一步將密度分布應用于模糊聚類優化過程，提升了聚類算法計算性能.數據集上的測試結果表明，本方法確實能夠提升非平衡數據聚類性能，而且能有效降低聚類迭代次數，展示出了處理大數據的潛力.

[1]Clark M C,Hall L O,Goldgof D B，et al.Mrisegmentationusingfuzzyclusteringtechniques[J].IEEE Eng Med Biol,1994，13(5):730-742.

[2]Beyan C,Fisher R.Classifyingimbalanceddatasetsusingsimilaritybasedhierarchicaldecomposition[J].Pattern Recogn，2015，48(5)：1653-1672.

[3]Noordam J C,Van den Broek W H A M，Buydens L M C,et al.Multivariateimagesegmentationwithclustersizeinsensitivefuzzyc-means[J].Chemometr Intell Lab Syst，2002，64(1)：65-78.

[4]Bensaid A M,Hall L O,Bezdek J,et al.Partiallysupervisedclusteringforimagesegmentation[J].Pattern Recogn，1996，29(5)：859-871.

[5]Gath I,Geva A.Unsupervisedoptimalfuzzyclustering[J].IEEE Trans Pattern Anal Mach Intell，1989，11(7)：773-781.

[6]Lin P L,Huang P W，Kuo C H,et al.Asize-insensitiveintegrity-basedfuzzyc-meansmethodfordataclustering[J].Pattern Recogn，2014，47(5)：2042-2056.

[7]Rodriguez A，Laio A.Clusteringbyfastsearchandfindofdensitypeaks[J].Science,2014，344(6191):1492-1496.

ImbalancedFuzzyClusteringMethodBasedonDataDensityPerception

WANGJin1,YOULei1,LIZhongwen1,MIAOFang2

(1.School of Information Science and Engineering, Chengdu University, Chengdu 610106, China; 2.Institute of Big Data, Chengdu University, Chengdu 610106, China)

Imbalanced data analysis is a key part in biomedical areas but poses a computational challenge for clustering methods due to the huge differences in the distribution between categories.This paper discusses the effects of imbalanced datasets on fuzzy clustering method based on imbalanced data clustering,and proposes a data-density-aware fuzzy clustering method to solve this problem.Specifically,a dataset is segmented into different areas with similar local density,and then a novel fuzzy clustering algorithm is implemented based on the initial partition.As a result,the initial clustering center point can be located and the disappearance of the minority class central point can be avoided.An updated method is further optimized based on data-density-aware fuzzy clustering,which is based on the above mentioned initial density method.The experimental results show that our method can better deal with the disappearance of the minority class in imbalanced datasets classification and compared with the traditional FCM,the clustering algorithm performance of the new FCM is obviously enhanced.

FCM;distribution density;imbalanced dataset

TP301.6

A

1004-5422(2017)04-0373-04

2017-08-25.

四川省教育廳自然科學基金(17ZA0082)資助項目.

王 進(1980 — )，男，博士，講師，從事機器學習相關技術研究.