預緊力對系統頻率漂移的影響

李太平，翁海寬，江浩，洪巖，齊曉軍

?

預緊力對系統頻率漂移的影響

李太平1,2，翁海寬1,2，江浩1,2，洪巖1，齊曉軍1,2

（1. 上海衛星裝備研究所；2. 上海裕達實業有限公司：上海 200240）

文章采用Harmonic的譜估計方法，研究了系統不同構件之間通過螺釘連接時，預緊力對系統動態特性的影響。在預緊力相同的情況下，不同量級的外界激勵，會造成系統表現出不同的頻率響應特性，呈現非線性時不變特性；大量級的外界激勵會造成系統預緊力“失效”，剛度降低，導致系統的固有頻率降低，產生頻率漂移，在共振處放大倍數降低。

預緊力；頻率漂移；共振；非線性；Harmonic譜估計方法；仿真分析；試驗驗證

0 引言

結構的固有頻率設計對結構和系統的可靠性具有重要意義。實際工作環境中，外界環境的變化會導致結構的固有頻率發生漂移，從而使系統的傳遞特性發生變化。如力學試驗中，滿量級振動試驗的結構固有頻率往往低于預振試驗中的固有頻率。這就導致了滿量級控制出現超差以及傳遞函數改變等。國內外對此開展了大量的研究，Woon等人[1]對結構的頻率漂移情況進行了大量的研究，但主要研究對象為工作溫度對系統頻漂的影響。Michel等[2]在實驗中檢測到了非常小的頻率漂移，并且演示了這種頻率漂移可能是由于激勵的變化引起的，同時，他們認為這種頻率漂移不可能是由于系統的結構參數發生了變化。薛宏偉等[3]對大量的頻率漂移現象和可能的原因進行了綜合分析。衛洪濤等人[4-6]也在此方面做了大量的研究，采用了帶間隙連接結構模型和螺栓連接結構的Iwan模型。Chowdhury等[7]研究了材料不同的結構阻尼比造成系統的頻率漂移。

以上的研究雖然在一定程度上解釋了系統的頻漂，但是也存在一定的不足：Woon等的研究無法解釋常溫下力學試驗中存在的頻率漂移，而Michel以及Chowdhury的理論都無法解釋實際力學試驗中存在的較大幅度的頻漂以及半功率帶寬不變的現象。衛洪濤的方法并沒有研究預緊力對系統傳函的影響，且由于其采用多點定頻取最大值的方法，獲得的為幅值譜而不是相位譜，與工程實際存在一定的偏差。

為了研究預緊力對系統頻率特性的影響，本文通過對數掃頻[8-9]獲得了一定量級激勵下系統的時域響應，進而通過Harmonic譜估計方法，估計系統的傳函。以帶間隙的兩自由度振動系統為例，對比小量級和滿量級掃頻實驗下傳遞函數的差異，以及加速度傳遞函數與位移傳遞函數的關系。最后通過某衛星力學試驗進行驗證。

1 對數掃頻

力學試驗中，一般采用掃頻的方法，獲得系統在特定激勵下的時域響應，進而通過特定的譜估計方法得到系統的傳函。本文采用常用的對數掃頻方法獲得系統的時域響應，系統在每個頻點處掃過的弧度一致，與頻率無關。對數掃頻過程中頻率隨時間改變，

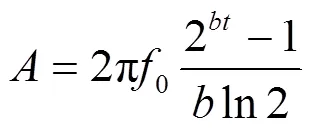
因此，系統在時刻的頻率為

定頻試驗（即=0）時，式(1)變為

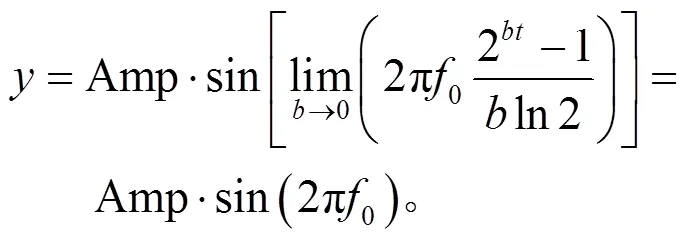
2 譜估計方法

通過對數掃頻的方法得到系統的時域響應后，需要通過一定的譜估計方法獲得系統的傳函。常用的譜估計方法有Harmonic、Peak、RMS和Average等4種。其中，Harmonic譜估計方法也被稱為Filter譜估計方法。

一般來說，這4種估計方法中，Harmonic譜估計方法的抗干擾能力最強，RMS和Average次之，Peak較弱；同時，Harmonic在估計出幅值譜的情況下，也能夠估計出相位譜，而其他3種方法均不能估計出相位譜。因此，本文選擇使用Harmonic譜估計方法。

在時間序列=0,1, …,t內，在激勵的作用下，采集到的時域響應序列為=[(1),(2), …,(n)]。該時間段內，任意時刻的時域響應都可以寫為y=sin(ωt+)，展開為y=sincos(ωt)+cos× sin(ωt)，對所有時間序列展開后，可得：

式(5)可寫成矩陣的形式

=cs。

由于微服務很難切得干凈,除了向外部提供以外，微服務之間難免會出現少量的調用關系，可將每次調用產生的相關信息寫入追蹤中心，通過追蹤中心提供的圖形化界面查看服務之間的調用軌跡和產生的調用延時，從而分析出服務調用產生的性能瓶頸。

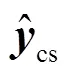
的值最小化。這需滿足

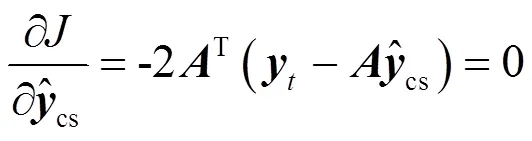
因此，cs的最小二乘估計為

獲得cs的最小二乘估計后，將()寫成()=sin(+)的形式，則相位為

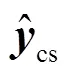
該相位即對應于傳遞函數中的相位譜。

3 帶間隙的兩自由度振動系統

為了研究預緊力對系統頻率漂移的影響，本文以通過螺釘連接的兩自由度振動系統（如圖1所示）為例進行了仿真研究。

1、2分別為m1、m2的位移，g為基座m0連接面的位移；2、2分別為m1、m2之間的彈簧阻尼系數；m1和m0之間通過螺釘J1、J2連接，在預緊力的作用下，m0產生了靜變形。因此，m1與m0之間的剛度為

其中：1c表示m1與m0之間的螺釘的連接剛度；1v表示基座在預緊力作用下產生靜變形對系統產生的附加剛度。

同時，在m1與m0之間存在一個固定的阻尼系數1。m0對m1存在一個位移擾動g，因此，整個系統的動力學方程可寫為

按照傳統的線性理論，若、、均為常值，則系統的傳遞函數可以表示為(2++)-1。但是由式(10)可得：系統的剛度矩陣會隨著m0和m1之間的位移發生變化，同時不顯含時間，因此該系統為非線性時不變系統，不存在確定的傳遞函數。

4 仿真分析

對整個系統進行掃頻試驗，起始頻率為5Hz，終止頻率為100Hz，掃頻速率為2oct/min，譜線數400。對系統作正則化處理：1c=2.45×104；1v=1× 104；2=8883；2=9.4248；1=15.708；=-3。取值為負，表示系統有預緊力存在，間隙為負值。采用MATLAB/SimuLink仿真，如圖2所示。其中，SubSytem即代表整個非線性時不變系統，k1即為式(10)中的1。通過Fcn模塊產生一個激勵施加在g上。當Fcn模塊輸出位移激勵時，直接作用在g上；當Fcn模塊輸出加速度激勵時，通過2次積分轉換為位移后，再作用在g上。

4.1 預試驗

進行預試驗時，由于試驗量級較低，式(10)中的1始終為1c+1v，系統表現為線性，整個系統存在傳遞函數。此時，通過小量級掃頻或者寬頻帶的隨機振動試驗獲得的傳遞函數是一致的。預試驗時式(1)中的Amp取值為0.1。圖3為預試驗過程中g、1、2的時域響應，從圖中可以明顯看出：小量級振動試驗過程中，相鄰周期的幅值連續可導。

圖4為預試驗輸入譜，其中上圖為幅值譜，下圖為相位譜。在整個頻帶內，輸入譜幅值均為0.1，相位均為0。

4.2 滿量級試驗

進行滿量級試驗時，試驗量級較高，剛度為1v的彈簧在大位移時處于自由狀態，因此系統表現出非線性，整個系統實際上不存在確定的傳遞函數。此時，通過大量級掃頻或者寬頻帶的隨機振動試驗獲得的傳遞函數都是不一致的，甚至可能同一功率譜密度的隨機振動試驗獲得的傳遞函數也是不一致的。滿量級振動試驗中，式(1)中的Amp取值為1。

圖5為滿量級振動試驗過程中g、1、2的時域響應。由圖可得：滿量級振動試驗過程中，各點的相鄰周期響應的幅值連續，但并非連續可導，在40s之后，出現了明顯的尖點。圖6為滿量級振動試驗過程中的輸入譜，全頻段幅值為1。

4.3 傳遞函數對比

圖7為m1預試驗和滿量級試驗中傳遞函數的對比，可以看出，在滿量級振動試驗過程中，系統剛度降低導致頻率前移，共振區域放大倍數降低。m2表現出的頻率漂移特性與m1類似（見圖8）。m1位移傳遞函數頻率漂移的特性如表1所示。

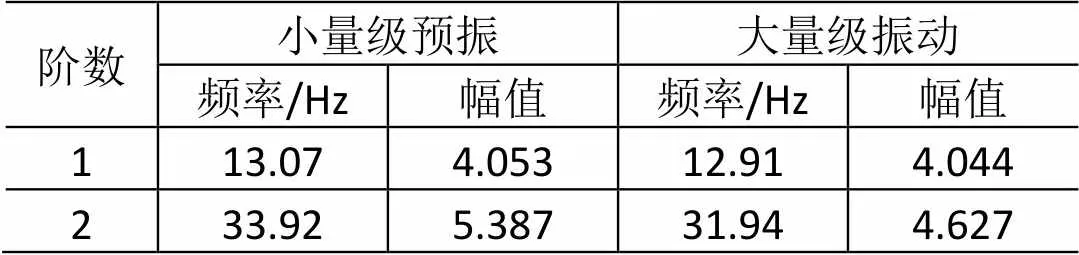
表1 m1位移傳遞函數頻率漂移

圖9為m2傳遞函數對比圖一階頻率處的局部放大，在13.47Hz處，預振試驗中系統的傳遞函數呈現光滑下降的趨勢；但是，滿量級振動試驗過程中，系統的傳遞函數呈現向上跳變。這與真實的力學試驗過程中出現的情況一致。圖10為m2傳遞函數對比圖二階頻率處的局部放大，可以看出，在二階頻率處，也發生了明顯的頻率漂移，且漂移幅度遠大于第一階固有頻率處的漂移量。

4.4 加速度與位移的傳遞函數

對于線性系統而言，式(11)中的、、均為常數，對其進行Laplace變換可得：

對于線性連續系統，進行Laplace變換可得：

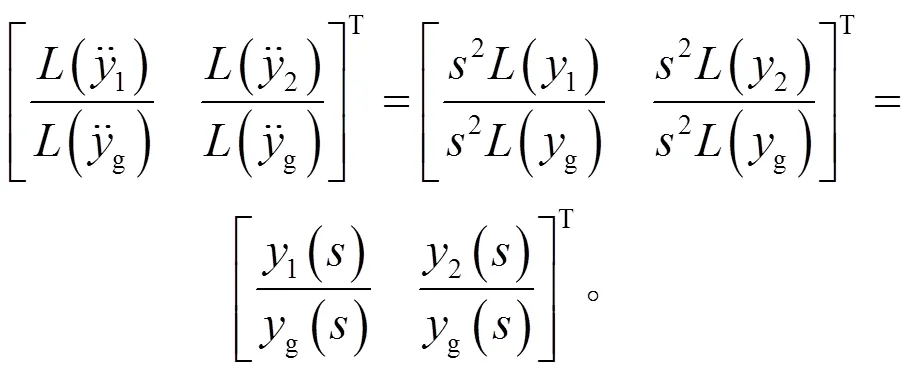
因此，在線性系統內，加速度傳遞函數與位移傳遞函數等效。但是對于存在間隙的系統，由于其為非線性時不變系統，所以不存在真正意義上的傳遞函數。通過譜估計的方法獲得的“傳遞函數”，其加速度和位移的“傳遞函數”并不等效。圖11、圖12所示為m1、m2的加速度與位移的“傳遞函數”，可以明顯看出，在共振區域，加速度和位移的“傳遞函數”并不等效。而在共振區域外，由于系統的間隙并沒有起作用，系統呈線性，加速度傳遞函數與位移傳遞函數之間關系滿足式(13)，所以加速度傳遞函數與位移傳遞函數等效。

5 試驗驗證

在某衛星的力學試驗過程中，首先進行了小量級的掃頻試驗，之后在完成大量級的掃頻試驗后，又進行了小量級的掃頻試驗，整個試驗過程的傳遞函數如圖13所示，在10～20Hz、35～45Hz、52～64Hz處的局部放大分別如圖14～圖16所示。

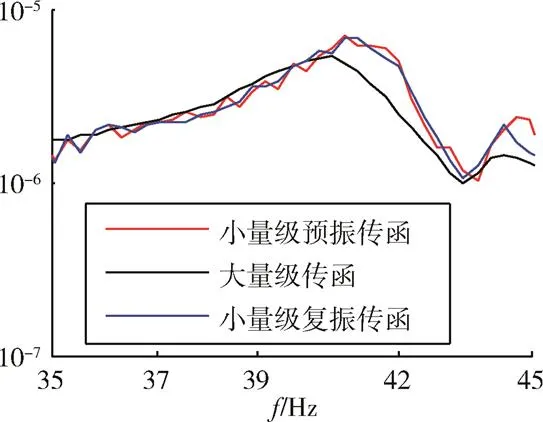
圖15 傳遞函數對比在35～45Hz處的局部放大

Fig. 15 Magnification of testing TFs at 35-45Hz

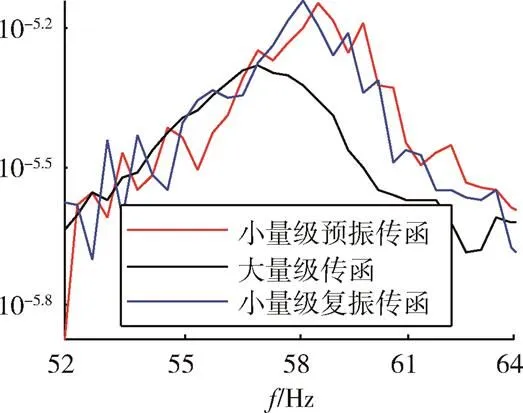
圖16 傳遞函數對比在52～64Hz處的局部放大

Fig. 16 Magnification of testing TFs at 52-64 Hz

三次試驗的前三階頻率對比如表2所示：小量級的預振和復振試驗基本沒有發生明顯的變化，而大量級振動試驗過程中，頻率和幅值均發生了明顯的變化，頻率前移，幅值降低，表明了式(10)的正確性。

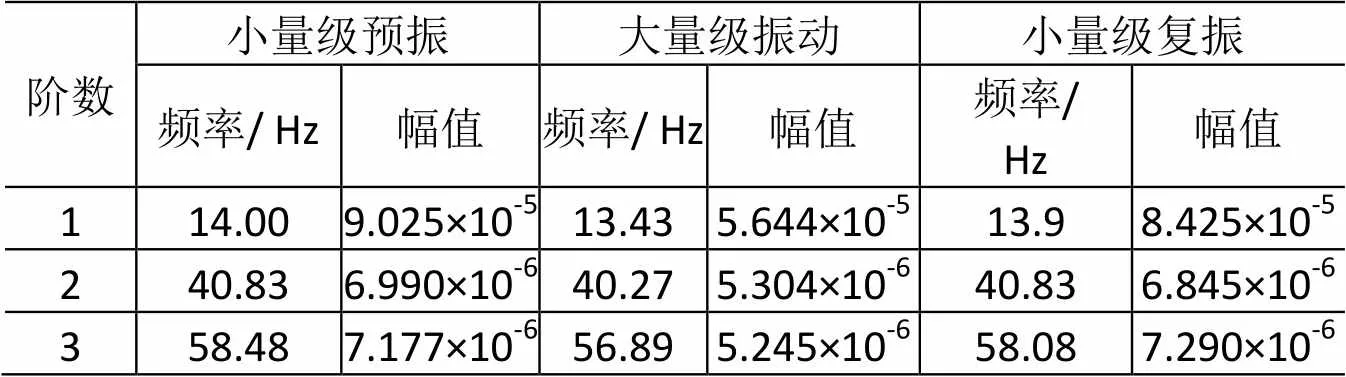
表2 三次試驗傳遞函數頻率漂移

6 結束語

系統不同構件之間通過螺釘等緊固件連接，連接螺釘上預緊力的大小會直接影響系統在不同外界激勵作用下的動態剛度，使系統的動態特性呈現非線性時不變特性，造成系統在大量級激勵下的動態剛度降低，固有頻率漂移等；同時，使系統的傳遞函數呈現不連續可導的情況，與實際的力學試驗中掃頻結果一致。工程實踐中，對于存在預緊力的系統，在設計結構固有頻率和研究傳遞特性時，應充分考慮系統的實際工作環境。

[1] WOON C E, MITCHELL L D. Variations in structural dynamic characteristics caused by changes in ambient temperature: I Experimental[J]. Proceedings of SPIE, 1996: 2768

[2] MICHEL C, GUéGUEN P. Time-frequency analysis of small frequency variations in civil engineering structures under weak and strong motions using a reassignment method[J]. Structural Health Monitoring, 2010, 9(2): 159-171

[3] 薛宏偉, 林益明, 劉天雄. 航天器振動試驗的頻率漂移問題綜述[J]. 航天器工程, 2005(4): 58-62

[4] 衛洪濤, 孔憲仁, 王本利, 等. 非線性連接結構對一個典型衛星頻率漂移的影響[J]. 航天器環境工程, 2012, 29(3): 297-303

WEI H T, KONG X R, WANG B L, et al. Effect of nonlinearities in the joints on the amplitude-frequency response of a typical satellite structure[J]. Spacecraft Environment Engineering, 2012, 29(3): 297-303

[5] IWAN W D. A distributed-element model for hysteresis and its steady-state dynamic response[J]. Journal of Applied Mechanics, 1966, 33(4): 893

[6] 王本利, 張相盟, 衛洪濤. 基于諧波平衡法的含Iwan模型干摩擦振子非線性振動[J]. 航空動力學報, 2013, 28(1): 1-9

WANG B L, ZHANG X M, WEI H T. Harmonic balance method for nonlinear vibration of dry friction oscillator with Iwan model[J]. Journal of Aerospace Power, 2013, 28(1): 1-9

[7] CHOWDHURY M A, HELALI M. The effect of amplitude of vibration on the coefficient of friction for different materials[J]. Tribology International, 2008, 41(4): 307-314

[8] 張步云, 陳懷海, 賀旭東. 多輸入多輸出正弦掃頻試驗控制新方法[J]. 振動與沖擊, 2015, 34(8): 198-202

ZHANG B Y, CHEN H H, HE X D. New control method for MIMO swept-sine test[J]. Journal of Vibration and Shock, 2015, 34(8): 198-202

[9] 張連朋. 雙水平向振動試驗臺正弦掃頻振動控制技術研究[D]. 哈爾濱: 哈爾濱工業大學, 2012: 17-20

（編輯：張艷艷）

The influence of preload on system frequency variations

LI Taiping1,2, WENG Haikuan1,2, JIANG Hao1,2, HONG Yan1, QI Xiaojun1,2

(1. Shanghai Institute of Satellite Equipment; 2. Shanghai Yuda Industrial Co., Ltd.: Shanghai 200240, China)

In this paper, the influence of the preload on the dynamic characteristics of a system with screw connections among different components is investigated with the harmonic spectrum estimation method. It is shown that with a preload of the same order of magnitude, the system exhibits different dynamic characteristics or FRFs under excitations of different orders of magnitude, as a non-linear time-invariant system. High level excitation may invalidate the preload, thus lead to reductions of the stiffness, the natural frequency, and the amplification in the resonance region.

preload; frequency variations; resonance; nonlinearity; Harmonic spectrum estimation method; simulation analysis; test validation

V416.2

A

1673-1379(2017)06-0636-06

10.3969/j.issn.1673-1379.2017.06.011

李太平（1989—），男，碩士學位，研究方向為結構振動測試與抑制。E-mail: litaiping168@126.com。

2017-05-13；

2017-11-30