基于PSO和SA多子群分層并行的智能分布式算法
邱千鈞,肖玉杰,曹 淵,于邵禎
(1.海軍駐航天二院代表室,北京 100854; 2.海軍裝備研究, 北京 100161)
【基礎研究】
基于PSO和SA多子群分層并行的智能分布式算法
邱千鈞1,肖玉杰2,曹 淵2,于邵禎2
(1.海軍駐航天二院代表室,北京 100854; 2.海軍裝備研究, 北京 100161)
針對PSO算法全局收斂性差、搜索精度不高,SA算法收斂速度慢,求解時間隨著問題規模的增大和復雜急劇增加的問題,提出一種PSO和SA多子群分層并行的智能分布式算法。算法底層是一個采用模擬退火策略搜索全局最優解的子群;上層是一系列粒子子群,采用粒子群優化算法搜索策略,貢獻局部最優解。算法從種群個體的組織結構出發,將局部搜索和全局搜索分離,使得PSO算法和SA算法融為一體,解決了算法收斂速度快和全局收斂能力強之間的矛盾。PSO-SAHP算法具有全局收斂性,算法在求解離散型的車間作業調度問題和連續型的Benchmark函數優化問題中,與單一智能優化算法相比,具有良好的可擴展性。這對于求解高度復雜的分布式問題,具有一定的工程意義。
混合算法;PSO算法;SA算法;智能分布式算法
粒子群(Particle Swarm Optimization,簡稱PSO)算法是Kennedy和Eberhart在1995年提出的一種新型群體智能優化算法[1-4]。粒子群優化算法簡單易實現、收斂速度快,在認知無線電參數優化[5]、函數極值尋優[6]、電弧爐供電優化[7]等實際問題中得到了廣泛的應用。模擬退火(Simulated Annealing,簡稱SA)算法是S.Kirkpatrick等人在1982年提出的一種模擬金屬退火機理而建立的隨機優化方法[8-9]。SA算法接受新模型的方式使其成為一種全局最優算法,并已得到理論和實際應用的驗證[10-14]。Information interaction
PSO算法和SA算法都是一種群體智能優化算法,都有自身的特點和優勢,同樣也都存在一些缺陷和不足。PSO算法簡單易實現,但搜索精度不高,且在理論上已經證明了其不是全局最優的[15];SA算法以概率1收斂于全局最優解,但其收斂速度慢,求解時間隨著問題規模的增大和復雜急劇增加[16]。
圖1所示為PSO算法和SA算法收斂速度的變化曲線,算法初期,PSO算法以很快的速度收斂到局部最優解,但隨著種群的不斷進化,算法的收斂速度急劇下降,甚至可能停滯不前,即算法出現“早熟”現象;SA算法雖然收斂速度緩慢,但其不斷接近最優解直至最終到達。鑒于PSO算法和SA算法有著幾乎互補的優勢,很多學者嘗試將兩者混合,取長補短,設計出很多性能更優的算法[17]。
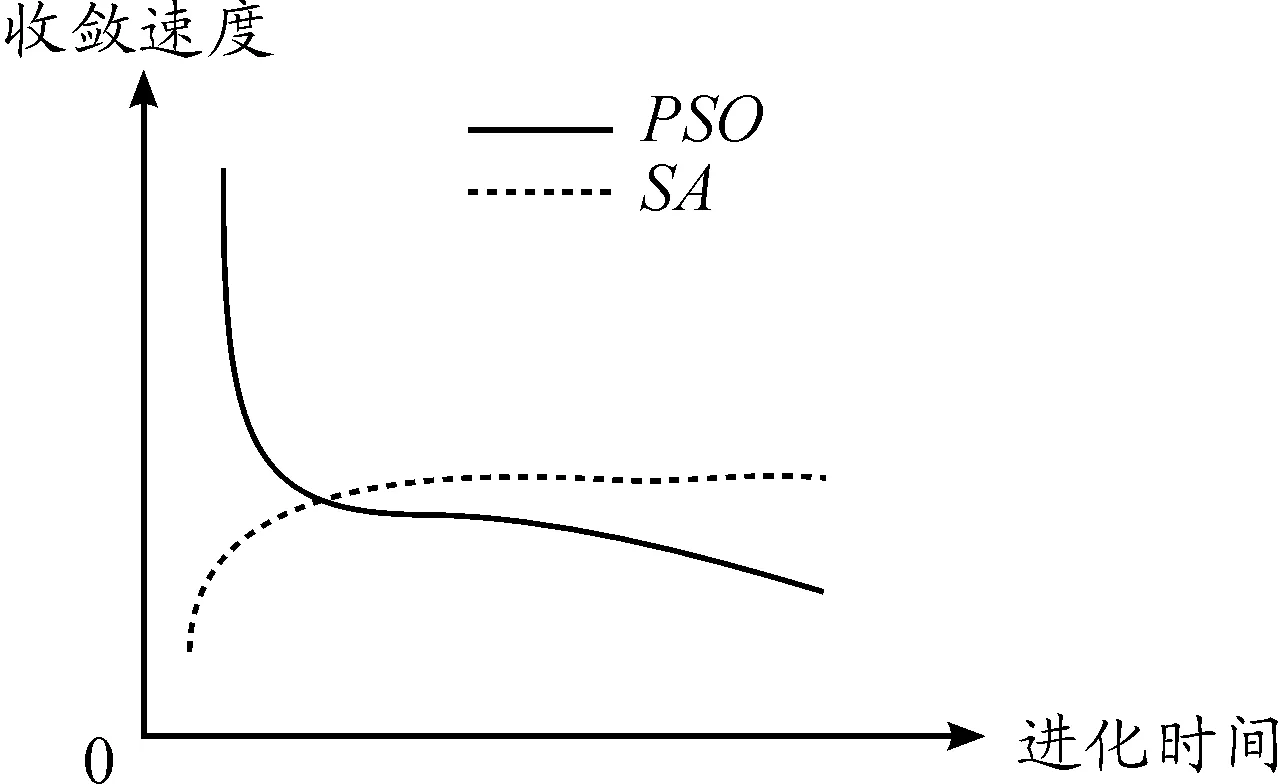
圖1 PSO算法和SA算法收斂速度變化曲線
近年來,混合算法的研究已經成為智能優化算法的主流方向[18-19]。如文獻[11,17]等結合PSO優化算法和SA算法各自的優點,提出了SA-DWPSO算法。通過PSO算法局部收斂性和SA算法全局收斂性的融合,有效的避免了PSO算法的早熟現象,加快了其收斂速度。
目前,混合算法主要有為串聯[20]和并聯[21-22]兩種混合形式。但這兩種混合方式都是將兩種算法以同等地位進行混合,兩種算法分工不明確,各自的優勢并沒有得到充分的發揮。
為了充分發揮PSO算法的快速尋優能力和SA算法的全局收斂特性,本文采用分層混合的思想,提出了一種PSO和SA混合的智能分布式算法。算法底層是一個采用模擬退火策略搜索全局最優解的子群;上層是一系列的粒子子群,采用粒子群優化算法搜索策略,貢獻局部最優解。算法從種群個體的組織結構出發,將局部搜索和全局搜索分離,使得PSO算法和SA算法有機的融合為一體,有效的解決了算法收斂速度快和全局收斂能力強之間的矛盾。
1 多子群分層并行的分布式算法
圖2所示為粒子群和模擬退火混合的多子群分層混合并行算法(以下簡稱PSO-SAHP算法)的種群個體組織方式,上層是整個算法的進化主體,在貢獻局部最優解的同時也為下層提供SA算法的初始值。由n個相互獨立的PSO子群組成,輸出局部最優值;下層采用模擬退火策略搜索全局最優解,PSO-SAHP算法可以解耦為如下兩個階段。
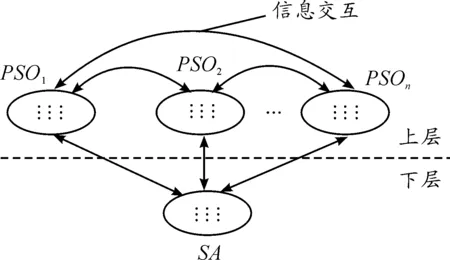
圖2 PSO-SA混合算法中的種群個體組織方式
階段1:啟動PSO算法搜索局部最優解,同時為底層SA算法提供初值。
首先,隨機初始化n個子群,分別記為PSO1、PSO2、、PSOn。每個子群獨立的在各自處理機上運行PSO算法,迭代一定代數后,進行信息交互(如將PSO1與PSO2中的某些個體進行交換),循環迭代一定代數后,取出各自的最優個體,選出最優解作為底層SA算法的初始值。
階段2:上層PSO子群和下層SA子群協同進化。
在計算過程中,兩種算法交替進行迭代,并通過比較目標函數值來判斷解的質量和協同進化方向。即如果上層的某個PSO子群搜索到較優的解,則從n個子群中隨機選取m個子群中的粒子,用該解替換原粒子的位置,并將其作為SA子群下一次迭代的初始位置;反之如果SA子群搜索到較優解,則隨機選取上層m個子群中的粒子,用該解替換原粒子的位置。需要指出的是此階段為了減少通信,上層PSO子群內部不再進行信息交互操作。
PSO-SAHP 算法的進化流程設計如圖3所示。
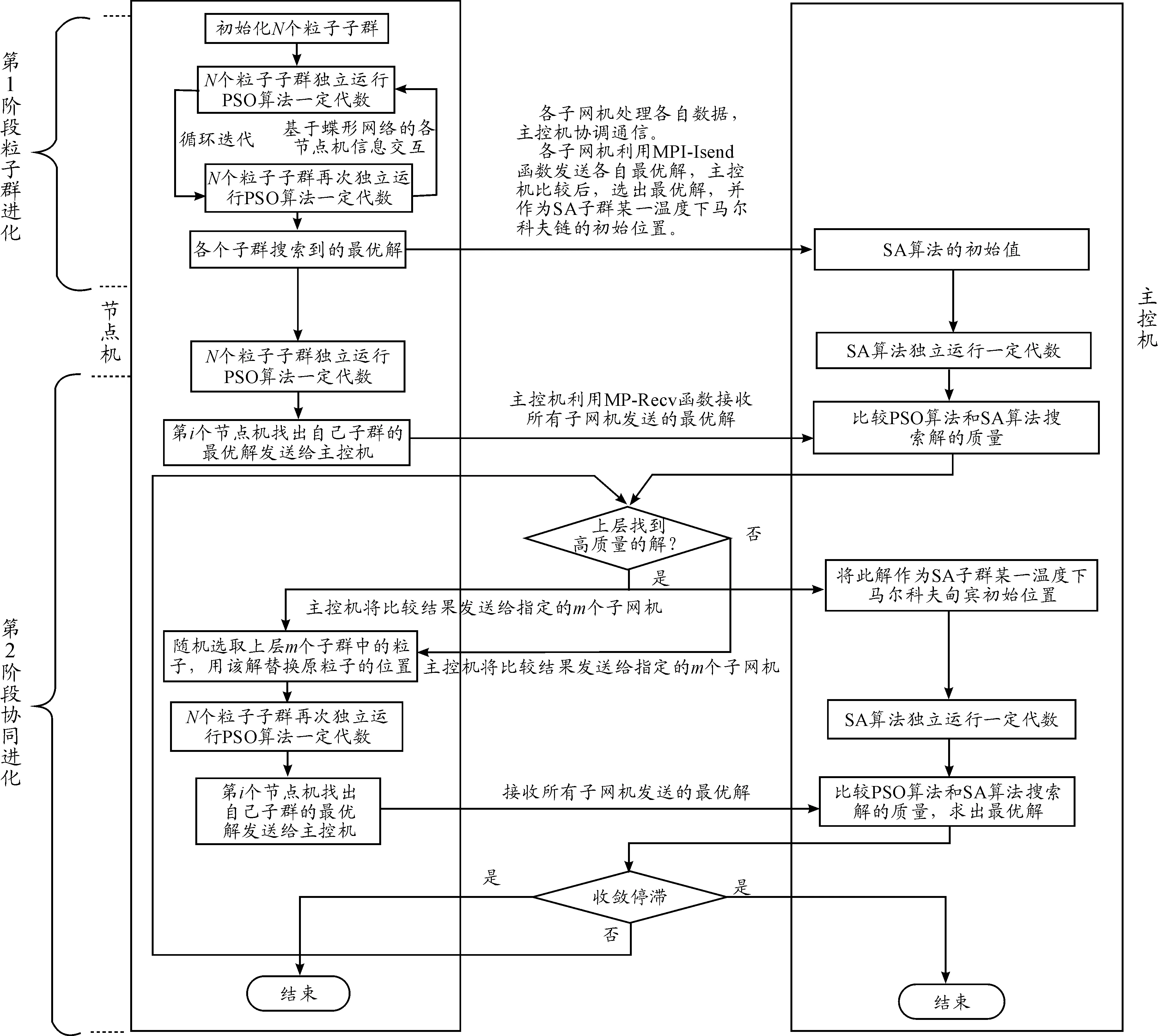
圖3 PSO-SAHP算法的進化流程
2 PSO-SAHP算法的全局收斂性證明
Solis和Wets給出了純隨機優化算法的收斂性判據,為了證明PSO-SAHP算法的全局收斂性,在此不加證明的列出了相關判定定理[23-24]。
(假設1 )對于優化問題〈S,f〉,若fDz,ξ≤fz,并且ξ∈S,則有fDz,ξ≤fξ。其中ξ是D算法在本次迭代過程中曾經搜索過的解。
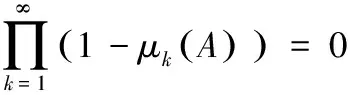
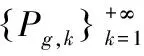
(定理)PSO-SAHP 算法以概率1收斂于全局最優解。
證明:設PSO-SAHP算法的迭代函數D為
(1)
其中,k是進化代數,Pg,k和Xg,k分別是PSO子群和SA子群第k代更新的全局最好位置,容易證明其滿足假設1[17]。
下面證明其滿足假設2:
粒子子群的樣本空間的并集必須包含解空間S,即
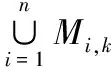
(2)
其中,Mi,k為第k代子群i樣本空間的支撐集。
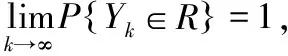
(3)
其中
(4)
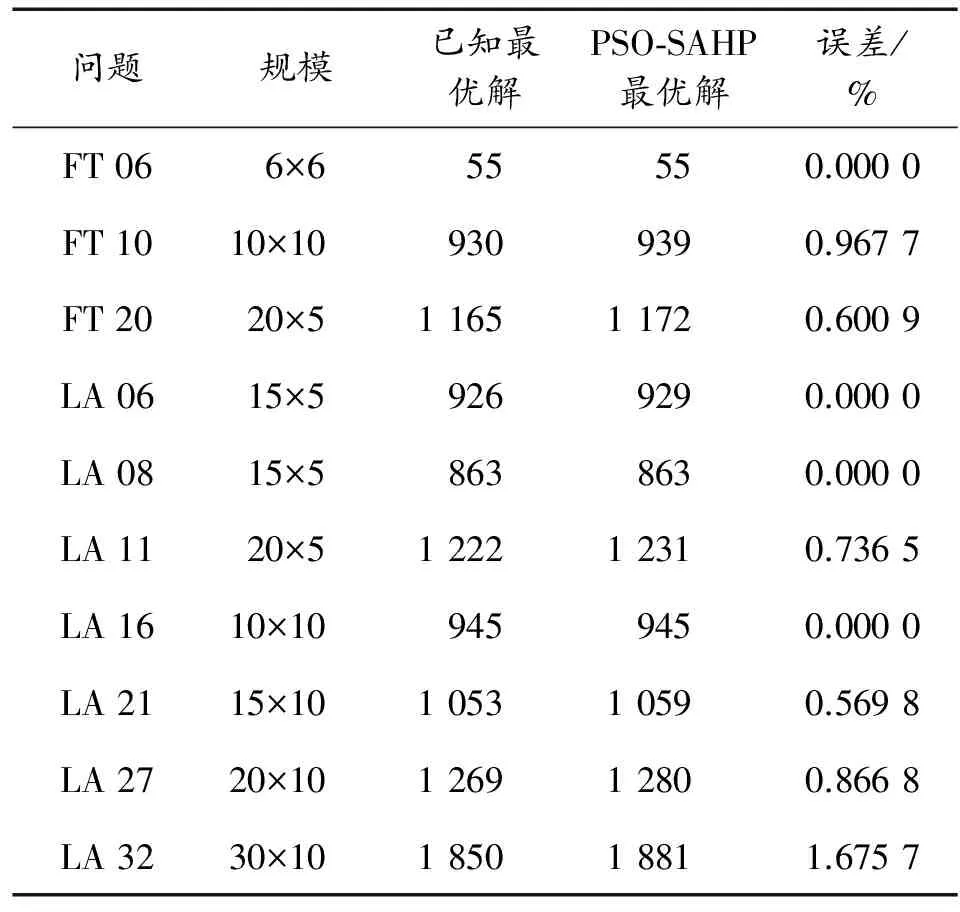
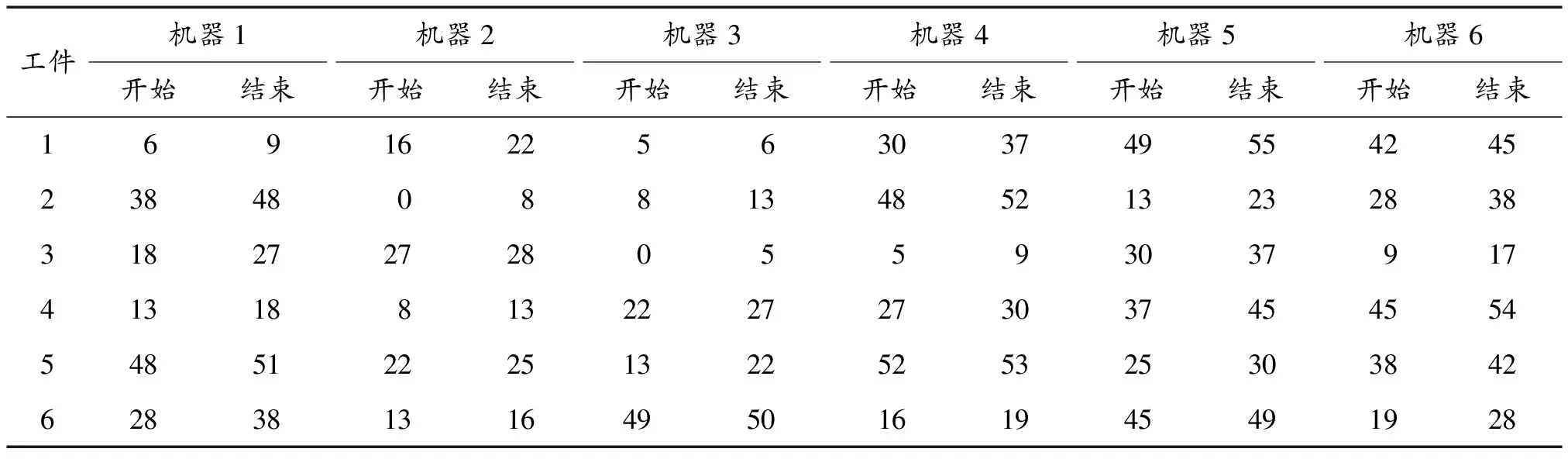
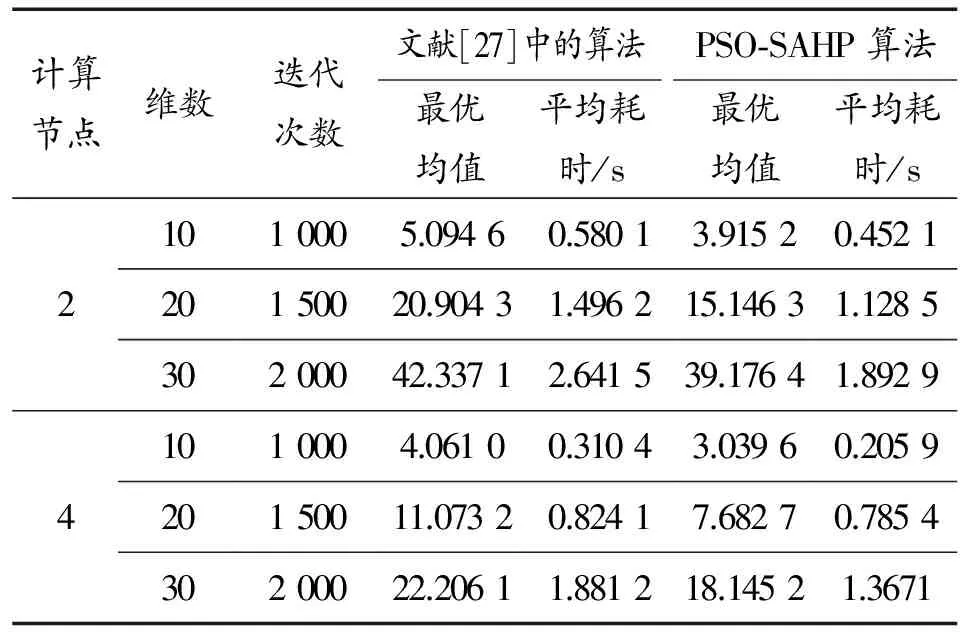
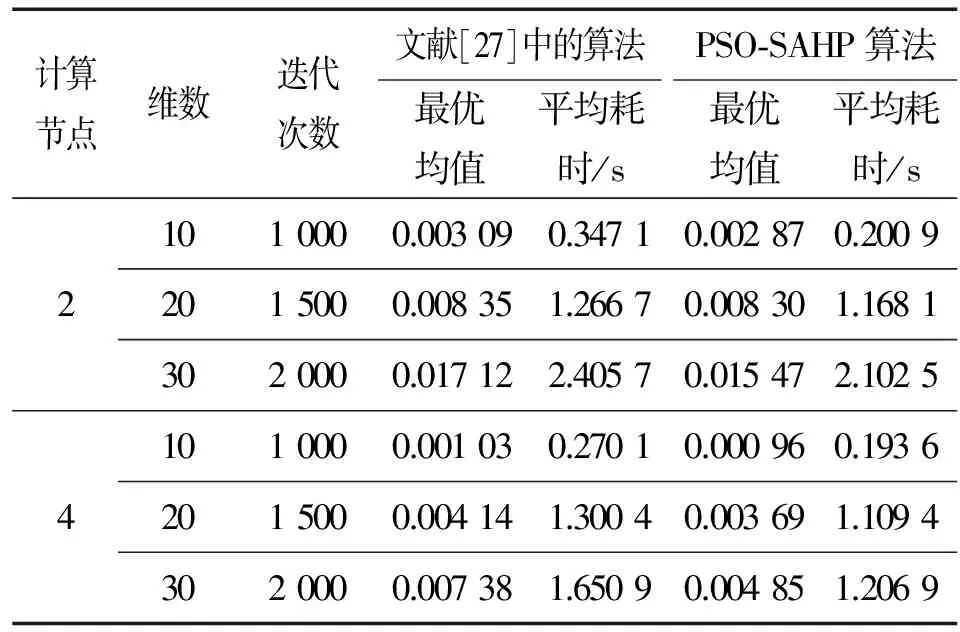
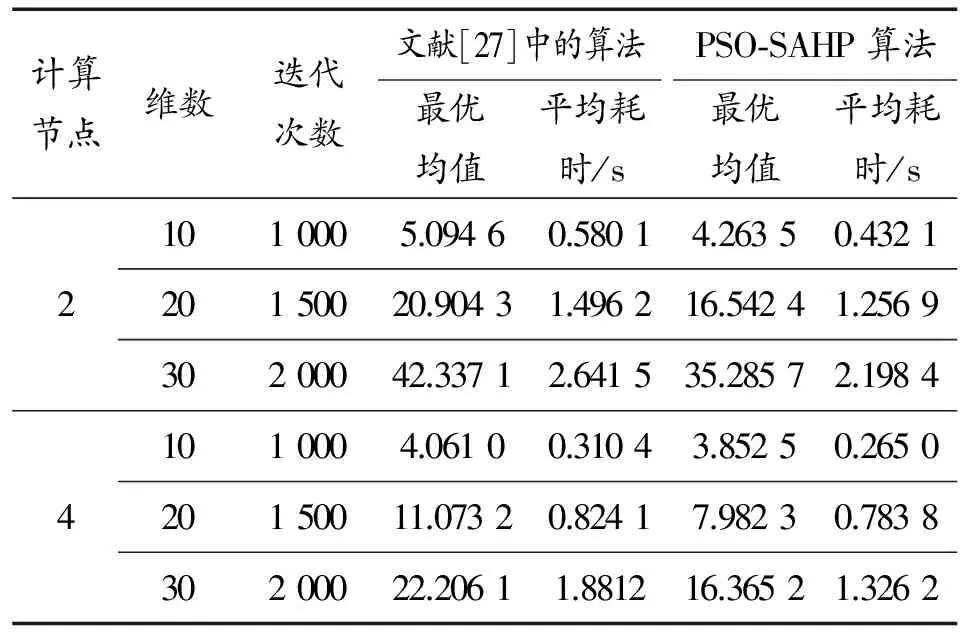
即當fYk Mi,k=Xik-1+ωXik-1-Xik-2+ φ1Pi,k-1-Xik-1+φ2Pg,k-1-Xik-1 (5) 其中,0≤φ1≤c1, 0≤φ2≤c2。 當式(5)成立時,顯然有vMi,k∩S maxc1Pi,j,k-1-xi,j,k-1,c2Pg,j,k-1-xi,j,k-1< 0.5·diamjS (6) 由引理1、2可知,PSO-SAHP算法以概率1收斂于全局最優解,故定理1成立。證畢。 為了驗證本文所提出的粒子群和模擬退火混合的多子群分層并行算法的有效性,將其應用于求解標準優化函數的測試問題,即離散型的車間作業調度問題和連續型的Benchmark函數優化問題,相關對比試驗及結果如下所示。 為了測試算法的可行性,選取典型的測試問題進行對比實驗。標準的測試問題主要有FT類、LA類等,分別由Fisher,Thompson和Lawrence等構造[25-26]。 實驗環境:基于MPI的并行編程環境,使用 C++編程語言,表1給出了PC機群的詳細配置情況。PSO算法中慣性權重線性下降ω=0.9,0.4,加速常數c1=c2=2.0。每個子群的規模為40,SA算法的種群規模為40,初始溫度T0=100,比例降溫衰減系數K=0.975,馬爾科夫鏈長度Lk=50。階段1和階段2的最大迭代均為1 000次,最大保持代數為10(最優值連續10代保持不變即視為收斂),根據需要PSO算法和SA算法每迭代10次進行一次通信操作,由于算法的隨機性和收斂特性等不同,需要增加不同子群之間的等待時間,但這是并行算法不可避免的。 實驗對比結果如表2所示,其中第3列為問題已知的最優解y,第4列為使用PSO-SAHP算法求得的最優解y′,誤差百分比Err(保留小數點后4位有效數字)計算如式(7)所示,表3列出了求解 FT06型車間作業調度問題的一個最優解。從對比結果可以看出,算法求得的誤差控制在2%以內,有效的解決了JSSP調度問題。 Err=×100% (7) 表2 車間作業調度問題對比實驗結果 從文獻[27]中選取3個基準函數進行對比分析,表4列出了這些Benchmark函數的定義,搜索空間、初始化空間、已知的最優解等基本信息。實驗軟硬件環境:為了和文獻[27]中(其唯一的參數α設置為從1.2到0.5線性減少)的結果對比,PC機群的計算節點分別取2、4個,當計算節點分別為2和4時,上層每個粒子的規模分別是為40和20, 其他設置同上。 對于每一個標準Benchmark函數,為了排除隨機性,運行50次并記錄最優解的平均值,即最優均值以及平均耗時,其結果如表5、6、7所示。 從表5、6、7可以看出,對于求解三個標準函數,PSO-SAHP算法運行50次的最佳均值和平均耗時明顯小于文獻[27]中的算法,這說明PSO-SAHP算法具有良好的可擴展性,優勢較明顯。 表3 FT06車間作業調度的一個最優解 表4 標準Benchmark函數 表5 Rosenbrock函數的對比實驗 表6 Griewank函數的對比實驗 表7 Rastrigrin函數的對比實驗 PSO和SA多子群分層并行的智能分布式算法底層是一個采用模擬退火策略搜索全局最優解的子群;上層是一系列的粒子子群,采用粒子群優化算法搜索策略,貢獻局部最優解。算法從種群個體的組織結構出發,將局部搜索和全局搜索分離,使得PSO算法和SA算法有機的融合為一體,有效的解決了算法收斂速度快和全局收斂能力強之間的矛盾。 相關試驗表明,PSO-SAHP算法在離散型問題和連續型問題的求解中,具有良好的可擴展性,優勢較明顯。需要進一步驗證PSO-SAHP算法在解決多無人機編隊協同航路規劃、電力系統仿真計算等工程領域問題中的有效性。 [1] Tao Q, CHANG H Y, YANG Y.A rotary chaotic PSO algorithm for trustworthy scheduling of a grid workflow [J].Computer & Operations Research,2011,38(5):824-836. [2] WANG G L, ZHAO G Q, LI H P.Research on optimization design of the heating/cooling channels for rapid heat cycle molding based on response surface methodology and constrained particle swarm optimization [J].Expert Systems with Applications, 2011, 38(6): 6705-6719. [3] GORAI A, GHOSH A.Hue-preserving color image enhancement using particle swarm optimization [C].2011 IEEE Recent Advances in Intelligent Computational Systems, Piscataway: IEEE, 2011:563-568. [4] 方偉,孫俊,謝振平,等.量子粒子群優化算法的收斂性分析及控制參數研究[J].物理學報,2010,59(6):3686-3694. [5] 趙知勁,徐世宇,鄭仕鏈,等.基于二進制粒子群算法的認知無線電決策引擎[J].物理學報,2009,58(7):5118-5125. [6] 高維尚,邵誠,高琴.群體智能優化中的虛擬碰撞:雨林算法[J].物理學報,2013,62(19):1-16. [7] 馮琳,毛志忠,袁平.改進多目標粒子群算法及其在電弧爐供電優化中的應用[J].控制理論與應用,2011,28(10):1455-1460. [8] MIAO H, TIAN Y C.Robot path planning in dynamic environments using a simulated annealing based on approach [C].Proceeding of 10th International Conference on Control, Automation, Robotics and Vision.Hanoi Vietnam, 2008:1253-1258. [9] 王麗芳,曾建潮.基于微粒群算法和模擬退火算法的協同進化方法[J].自動化學報,2006,32(4):630-635. [10] 蒲榮富,肖思和,許多.模擬退火算法優化分析與應用研究[D].成都:成都理工大學,2013. [11] 林令娟,劉希玉.模擬退火微粒群混合算法的研究及應用[D].濟南:山東師范大學,2010. [12] 任子暉, 王堅, 高岳林.馬爾科夫鏈的粒子群優化算法全局收斂性分析[J].控制理論與應用,2011,28(4):462-466. [13] 金欣磊, 馬龍華, 吳鐵軍, 等.基于隨機過程的PSO收斂性分析[J].自動化學報, 2007, 33(12): 1263 - 1268. [14] VAN DEN BERGH F, ENGELBRECHT A P.A study of particle swarm optimization particle trajectories [J].Information Sciences, 2006, 178(8): 937 - 971. [15] 金 敏,魯華祥.一種遺傳算法與粒子群優化的多子群分層混合算法[J].控制理論與應用,2013,30(10):1231-1238. [16] 周 杰,俎云霄.一種用于認知無線電資源分配的并行免疫遺傳算法[J].物理學報,2010,59(10):7508-7515. [17] 趙知勁,鄭仕鏈,尚俊娜,等.基于量子遺傳算法的認知無線電決策引擎研究[J].物理學報,2007,56(11):6760-6706. [18] 俎云霄,周杰.基于組合混沌遺傳算法的認知無線電資源分配[J].物理學報,2011,60(7):7950-7957. [19] LI S T, WU X X, TAN M K.Gene selection using hybrid particle swarm optimization and genetic algorithm [J].Soft Computing, 2008, 12(11): 1039-1048. [20] MARINAKIS Y, MARINAKI M.A hybrid genetic—particle swarm optimization algorithm for the vehicle routing problem [J].Expert Systems with Applications, 2010, 37(2): 1446-1455. [21] KUO R J, SYU Y J, CHEN Z Y.Integration of particle swarm opti-mization and genetic algorithm for dynamic clustering [J].Information Sciences, 2012, 195: 124-140. [22] KAO Y T, ZAHARA E.A hybrid genetic algorithm and particle swarm optimization for multimodal functions [J].Applied Soft Computting, 2008, 8(2): 849-857. [23] SOLIS F,WETS R.Minimization by random search techniques [J].Mathematics of Operations Research, 1981,6(5):19-30. [24] 李寧,孫德寶.粒子群優化算法的理論分析與應用研究[D].武漢:華中科技大學,2006. [25] GAO J,GEN M,SUN L,et al.The particle swarm optimization algorithm convergence analysis and parameter selection[J].Information Processing Letters, 2003, 85(6): 317-325. [26] ZHANG Jing,WANG Wannian,XUN Xinli.Improved particle swarm algorithm for batch splitting flexible job shop scheduling [J].Control and Decision,2012,27(4):513-518. [27] 王小根,奚茂龍,須文波.具有量子行為粒子群優化算法的并行化研究[J].計算機工程與應用,2009,45(11):45-45. AnIntelligentDistributedAlgorithmofMulti-SubgroupHierarchicalHybridofSimulatedAnnealingAlgorithmandParticleSwarmOptimization QIU Qianjun1, XIAO Yujie2, CAO Yuan2, YU Shaozhen2 (1.Navy Representative office in the Second Academy of CASC, Beijing 100854, China;2.Naval Academy of Armament, Beijing 100161, China) To make use of the strong global search ability of the simulated annealing algorithm and the high convergence rate of the particle swarm optimization, we combine these two algorithms and propose an intelligent distributed algorithm of multi-subgroup hierarchical hybrid of simulated annealing algorithm and particle swarm optimization (PSO-SAHP).This hybrid algorithm adopts a hierarchical structure; the base level is composed of a series of subgroups of simulated annealing algorithm, which provides the global search ability of the entire algorithm. The top level comprises all elite subgroups consisting of the best individual of each subgroup, which performs the accurate local search by using the particle swarm algorithm with cramped initial velocity. The global convergence analysis of PSO-SAHP is given in this paper, algorithm for solving discrete job shop scheduling continuous optimization problem of Benchmark functions,compared with single algorithm,has good scalability and obvious advantages. It has some engineering significance for solving highly complex distributed computing problems. compound arithmetic; PSO-SAHP; SA algorithms; intelligent distributed algorithm 2017-09-13; 2017-09-30 邱千鈞(1990—),男,碩士,主要從事艦載武器研究。 10.11809/scbgxb2017.12.057 本文引用格式:邱千鈞,肖玉杰,曹淵,等.基于PSO和SA多子群分層并行的智能分布式算法[J].兵器裝備工程學報,2017(12):261-266. formatQIU Qianjun, XIAO Yujie, CAO Yuan, et al.An Intelligent Distributed Algorithm of Multi-Subgroup Hierarchical Hybrid of Simulated Annealing Algorithm and Particle Swarm Optimization[J].Journal of Ordnance Equipment Engineering,2017(12):261-266. TP301.6 A 2096-2304(2017)12-0261-06 (責任編輯楊繼森)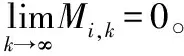
3 PSO-SAHP 算法的實驗測試
3.1 車間作業調度問題的對比實驗
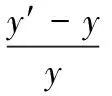
3.2 Benchmark函數優化問題的對比實驗

4 結論

