脈沖修正彈藥技術研究

陳勝政，楊 波，楊栓虎，杜鳳懷，宋宇航，楊 力，高曉波

(西安現代控制技術研究所， 西安 710065)

【彈藥工程】

脈沖修正彈藥技術研究

陳勝政，楊 波，楊栓虎，杜鳳懷，宋宇航，楊 力，高曉波

(西安現代控制技術研究所， 西安 710065)

針對無控彈藥低成本精確打擊的使用需求，提出了采用脈沖發動機作為執行機構的脈沖修正彈藥技術方案，開展了脈沖修正控制、修正策略、點火策略建模研究，并對脈沖修正彈藥修正原理及精度進行了仿真分析。仿真分析表明，脈沖修正彈藥原理可行，命中精度不顯著弱于氣動舵機，驗證了脈沖修正彈藥技術原理的可行性。

脈沖修正彈藥；脈沖發動機；修正控制；修正策略

無控彈藥具有威力幅員大、火力猛、作戰反應時間短、成本低等優點。與之對應地，也存在附帶損傷大、命中精度低、無法應對高價值點目標或點-面目標等缺點。

脈沖發動機具有成本低、反應時間短、可靠性高、點火延遲散布小等優點，可在短時間內產生大推力，以上特點使得脈沖發動機十分適合作為修正彈藥的執行機構來進行彈道的閉環控制。此外，相比氣動舵機，該型修正彈藥無需增加舵面和采用大尾翼方案，不僅彈體結構改動小，氣動阻力也更小，是一種更適合修正彈藥的執行機構。

脈沖修正彈藥是一種在無控彈藥基礎上，采用衛星或低成本末端尋的導引頭進行自身位置或目標信息測量，并通過加裝脈沖發動機作為執行機構，按一定的制導控制律進行彈道閉環修正控制的一種精確打擊彈藥。

由于采用了彈道閉環控制，脈沖修正彈藥的命中精度大幅度提高。使得其不僅具備攻擊點-面目標的能力，甚至具備攻擊點目標的能力，大大拓展了作戰能力和綜合作戰效能。

基于此，國外在脈沖修正彈藥技術上做了大量研究，已有多個產品裝備部隊或出口使用，在多次局部戰爭中發揮了重要作用。典型的有俄羅斯的“勇敢者” 240毫米脈沖修正迫彈、152mm末修炮彈“SANTIMETR”、BM-8航空修正火箭，瑞典的strix120毫米紅外末制導迫彈，美國的ATK公司的XM395精確制導迫彈、通用動力公司的滾轉控制制導迫彈等。由于采用了脈沖修正技術，該型制導彈藥的打擊精度均提高到了10m之內，大大提高了武器系統平臺的作戰能力。

1 脈沖修正彈藥原理

1.1 脈沖修正彈藥簡介

脈沖修正彈藥一般由無控彈藥發展而來，在無控彈藥彈體頭部加裝探測組件以及信息處理單元，作為彈上制導信息獲取、信息處理以及綜合管理的核心單元。

探測組件一般包括衛星定位儀或低成本的末端尋的導引頭，以及二者的復合體。衛星定位儀可實時測量自身位置坐標，為彈藥修正控制提供自身位置信息。低成本的末端尋的導引頭在末端可實時探測目標，并測量彈目相對位置信息。

信息處理單元不僅進行信息處理，還集成了姿態測量單元，為控制指令實時解算提供彈體姿態信息。

在彈身質心位置安裝一系列周向均布、噴口朝外的脈沖發動機，作為彈道修正控制的執行機構。由于脈沖發動機與彈軸垂直安裝，其推力垂直于彈軸，其工作時產生的推力直接作用在質心上，可直接改變彈藥質心速度方向，從而實現彈道修正。

典型的脈沖修正彈藥布局示意圖見圖1。

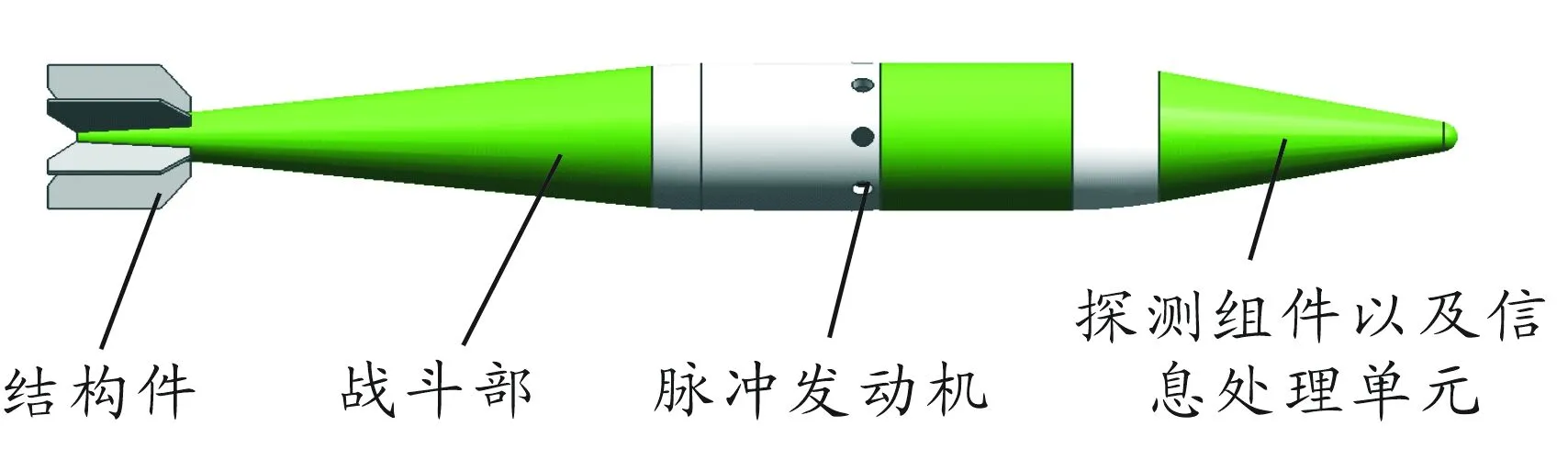
圖1 脈沖修正彈藥布局示意圖

脈沖發動機在彈身截面的安裝示意圖見圖2。

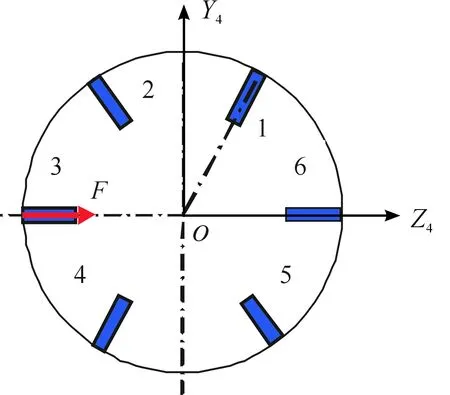
圖2 脈沖發動機在彈身截面的安裝示意圖

在圖2中，以3#脈沖發動機為例，工作時產生的尾噴流是指向負Z軸，形成的推力指向+Z軸，從而將彈道向右側修正。

1.2 脈沖修正彈藥工作原理

以衛星制導脈沖修正彈藥為例說明。

發射以前，射手先向其裝定目標坐標或衛星星歷。發射出去以后，脈沖修正彈藥通過衛星定位儀實時測量自身位置坐標及速度信息，并送給信息處理單元。信息處理單元實時敏感并測量彈體姿態信息。信息處理單元綜合衛星定位儀送出的彈藥質心位置、速度信息及自身測量到的彈體姿態信息，按一定的修正控制算法，實時解算出脈沖發動機的點火時機及發動機編號。當飛行時間到達規定的點火時機，信息處理單元向選定的脈沖發動機給出點火信號，點燃脈沖發動機。脈沖發動機工作產生橫向推力，修正彈藥速度方向，逐步減小與目標的偏差，直至命中目標。脈沖修正彈藥工作原理見圖3。

2 脈沖修正控制數學模型

2.1 單次脈沖修正量計算

按圖3所示，以t時刻點燃3#脈沖發動機為例，建立單次脈沖修正量數學模型。

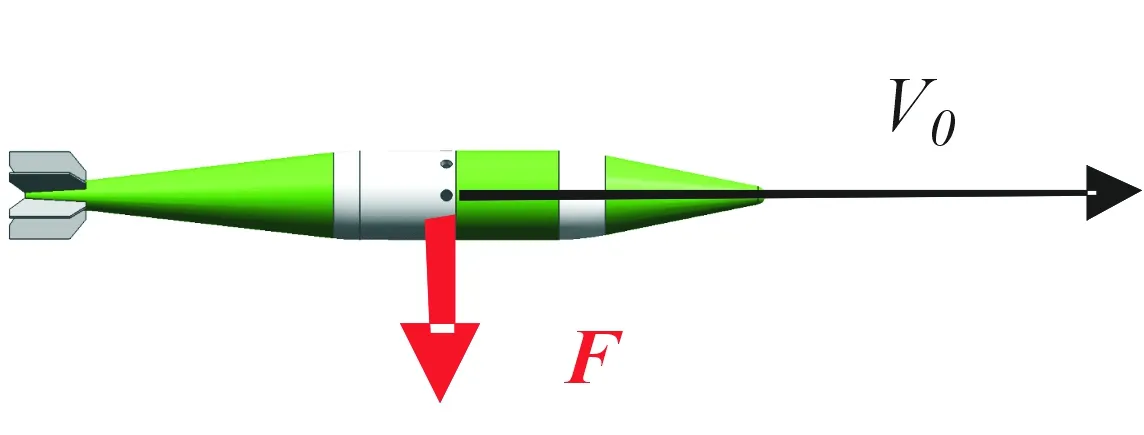
圖3 t～t+Δt時刻彈藥受力情況

記單個脈沖發動機的總沖為I、工作時間為Δt，平均推力為F。那么：

I=FΔt

(1)

t時刻點燃發動機后，彈藥質心將會受到橫向力F的作用，直至t+Δt時刻結束。在t～t+Δt時刻彈藥受力情況見圖3。t時刻彈藥運動速度記為V0。

在t+Δt時刻，彈藥將獲得一個與F方向相同的橫向速度，記為ΔV。此時，彈藥的運動速度應為V0與ΔV的合成，記為V1。如圖4。

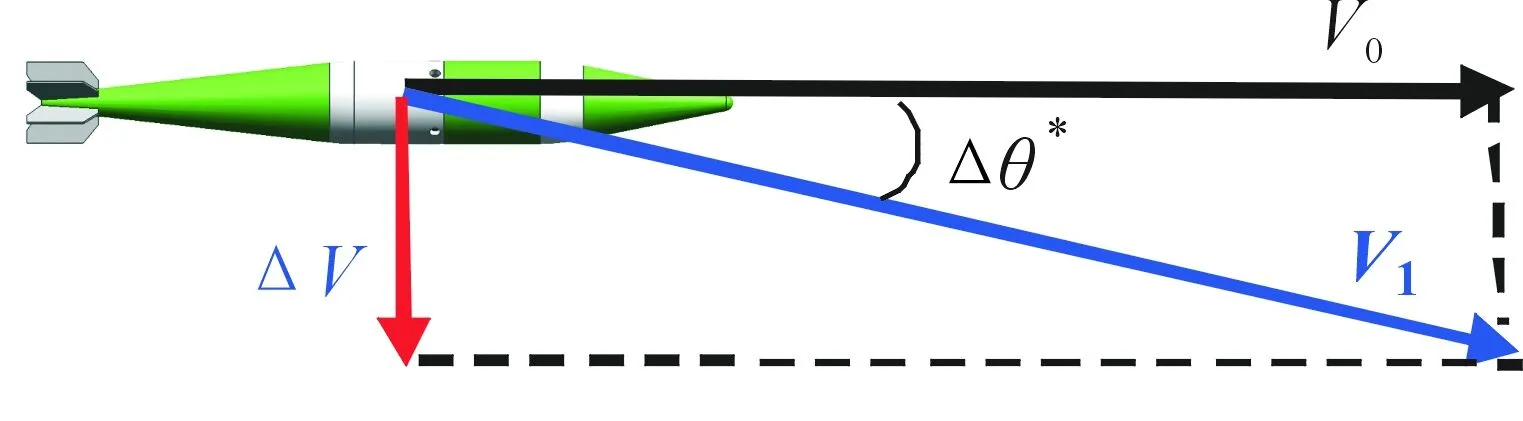
圖4 t+Δt時刻彈藥運動速度

合成速度V1顯然與V0方向不一致，方向改變量記為Δθ*，那么：

Δθ*=57.3×tg-1(ΔV/V0)≈57.3×ΔV/V0

(2)

另一方面， 根據動量守恒原理，彈藥在脈沖發動機作用下，將產生動量改變量，其值恰好等于3#發動機的沖量I。即：

I=FΔt=Δ(mV0)=mΔV

(3)

ΔV=I/m

(4)

將式(4)代入式(2)，則有：

Δθ*=57.3×I/(mV0)

(5)

式(5)即為單次脈沖發動機產生的修正量。由于該修正量為角度，可稱之為角度修正量。

角度修正量改變了彈藥飛行方向，隨著時間累積，將改變彈藥最終的落點，從而實現對命中點的修正。

與氣動舵機相比，氣動舵機的最終控制效果也是改變彈藥的速度方向。由此可見，在原理上，兩種執行機構是等效的。所不同的是，氣動舵機是連續、線性修正。

由式(5)可見，脈沖發動機的角度修正量大小與單個發動機總沖成正比，與彈體質量、速度成反比。

當發動機比沖、彈體質量設計完成，在當前速度下，單次脈沖修正引起的角度修正量Δθ*就是一定的，不能隨意調節，這是脈沖修正的一個主要缺點，即修正能力不能任意調節。對比氣動舵機，脈沖發動機無法實現線性、連續修正，因而控制精度差與氣動舵機。

2.2 彈道修正的數學模型

由式(5)可見，單次修正完成后，將改變了彈藥的速度方向。而實際需要的修正量是距離偏差，因此需要將距離偏差轉換成角度偏差。距離修正量示意圖如圖5。

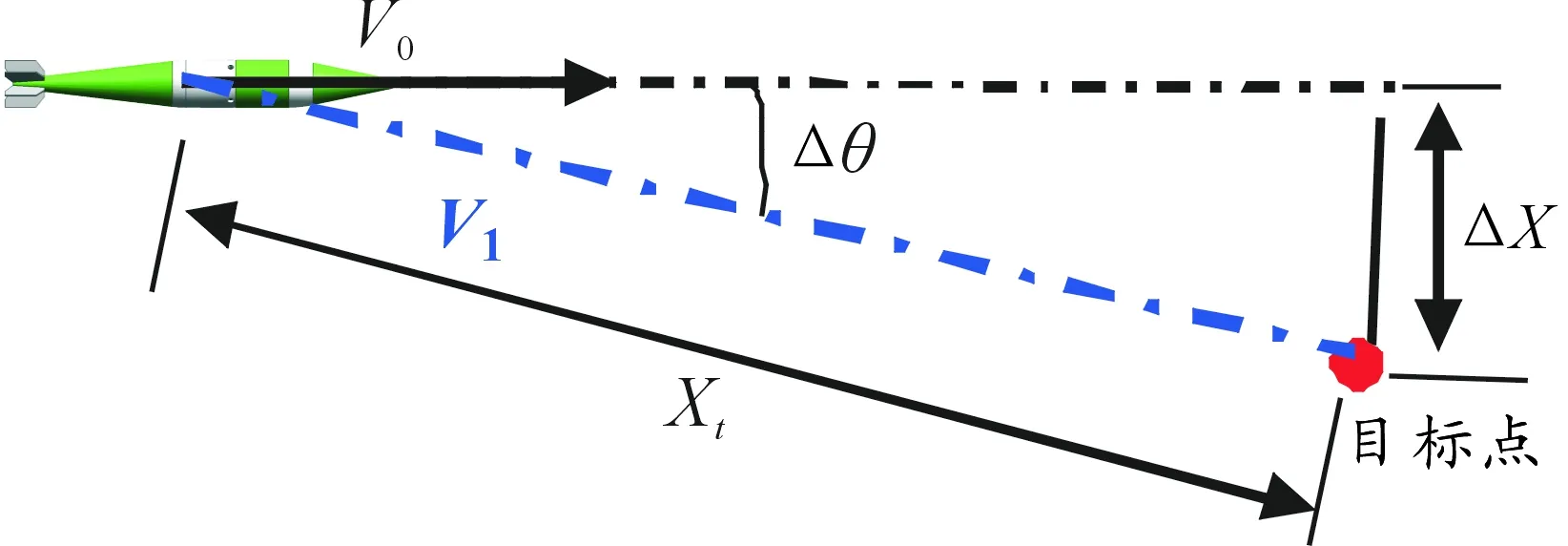
圖5 距離修正量示意圖

圖5中，若t時刻不修正，那么彈藥沿著當前速度V0飛行，最終將形成脫靶量ΔX。

若彈藥的剩余飛行距離為Xt，那么脫靶量ΔX對應的角度修正量為：

Δθ=sin-1(ΔX/Xt)× 57.3

(6)

式(6)即為距離修正量到角度修正量的轉換關系。即在t時刻，修正Δθ之后，即可消除脫靶量ΔX，實現彈藥對目標的命中。

實際運用時，由于彈藥當前位置坐標可由衛星定位儀實時解算出來，而目標位置坐標發射前已經裝訂，那么Xt是實時已知的。ΔX可通過落點預測等算法解算出來。

具體運用時，彈藥相對于目標的偏差角一般可分為俯仰偏差角ΔθFY和偏差角ΔθPH。那么，Δθ應為俯仰偏差角和偏差角的合成角。即：

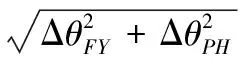
(7)

此外，還有誤差相位的問題，誤差相位Φ：

Φ=57.3×atan(ΔθFY/ΔθPH)

(8)

Φ決定了修正量的方位。

2.3 彈道修正策略

由式(5)可知，修正一次將使得速度方向變化Δθ*，該值在彈體質量、速度、發動機總沖確定的條件下，是個定值。

但由式(7)解算的彈道偏差Δθ卻是任意的，當其值角不足Δθ*時，那么修正一次是不必要的。也就是說，是否修正一次，應以Δθ*為閾值，這就是需要遵循的修正策略。

那么，修正策略為：

Δθ≥Δθ*

(9)

2.4 脈沖發動機點火策略

當t時刻需要執行一次修正時，由于有多個脈沖發動機備選，那么究竟該點哪一個、何時點燃發動機才能達到修正效果呢？這存在一個點火策略的問題。

脈沖發動機點火策略確定原理見圖6所示。

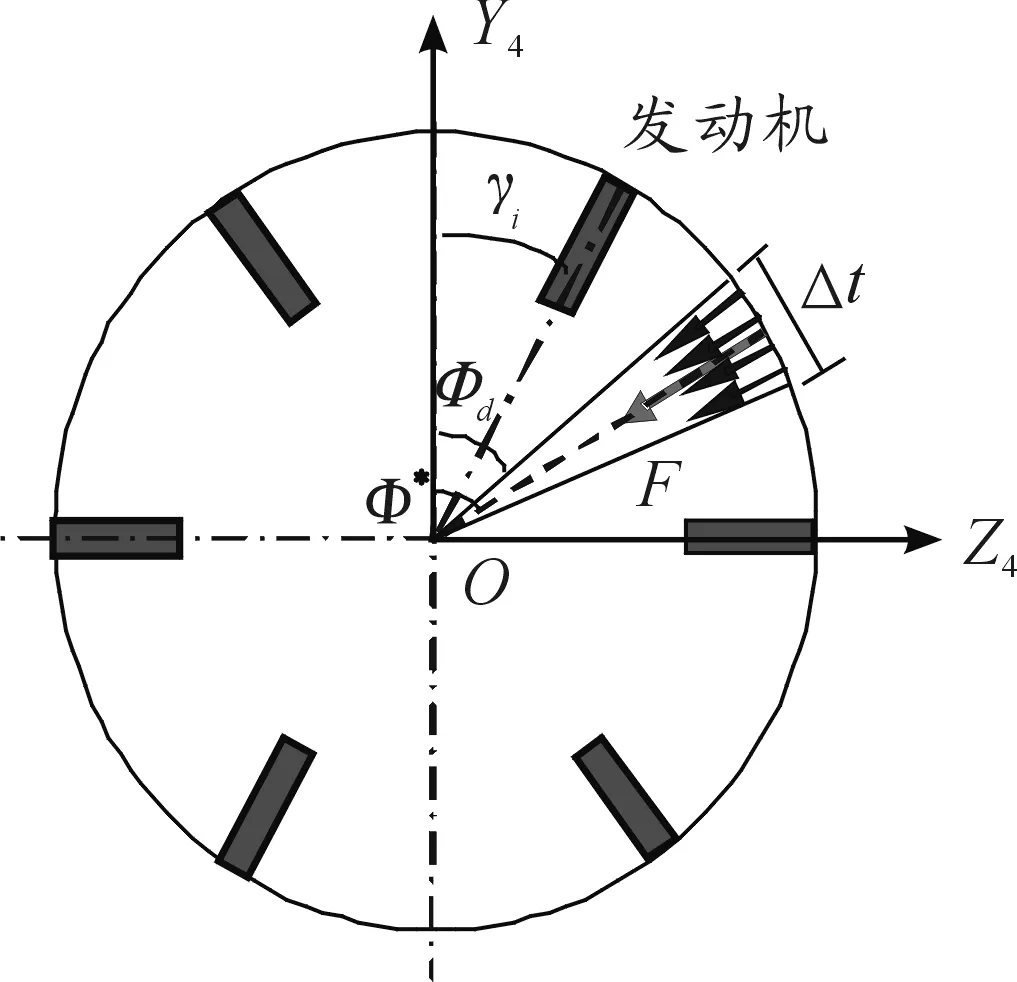
圖6 點火策略確定原理示意圖

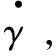
(10)

由以上論述可見，在式(9)滿足后，還需要判斷是否正好存在一個發動機的相位達到式(10)的要求，且該發動機尚未點火工作過。

若當前沒有滿足式(10)的發動機，由于發動機隨著彈體在不停地旋轉，只要還有多于一個的發動機有效，那么只需要等待某一個有效的發動機旋轉到滿足式(10)，那么就可點燃該發動機完成1次彈道修正控制。這就是應遵循的點火策略。下面建立數學模型。

假設共n個發動機，發動機標號分別為1,2，…,n。

當前時刻第i(i是1～n中的任意一個)個發動機的滾轉方位為γi，Di表示第i個發動機的是否有效的狀態。初始時刻，全部發動機均有效，即Di=1(=1～n)。發動機m工作一次后便失效，Dm賦0值，隨后的點火策略里需自動排除發動機m。

用Δγ(i)表示第i個發動機與點火相位之間的角度差φdh，對于無效發動機(Di=0)，將其相位Δγ(i)賦值為∞。那么：

(11)

式(11)即為計算各個發動機與要求的點火相位之間的相位差。

根據式(11)計算的各個發動機與點火相位Φ*的相位差，最小值對應的那個發動機即為最近的發動機，點燃最近的發動機，無疑是修正誤差最快的，因而是最優的策略。

點火策略按下式定：

(12)

式(11)、式(12)便是點火策略數學模型。

3 仿真算例

本文第2節完成了修正控制數學模型的建模，將該模型編制成計算程序，輸入仿真條件，即可進行脈沖修正控制仿真計算。通過仿真計算，能夠對修正控制原理的正確性、修正精度進行仿真計算。下面以某修正彈藥為例進行仿真計算分析。

3.1 仿真條件

單個脈沖發動機總沖：70 N·s；飛行距離：6 700 m；啟控時間：9 s；彈體轉速：6 r/s：彈藥質量：22 kg。

3.2 修正彈道仿真

仿真計算得到的上下邊界彈道曲線見圖7，發動機點火信號圖見圖8，啟控后的誤差角曲線見圖9。

由以上計算可見，啟控后，上下邊界彈道均開始收斂，最終命中目標，實現了彈道修正。

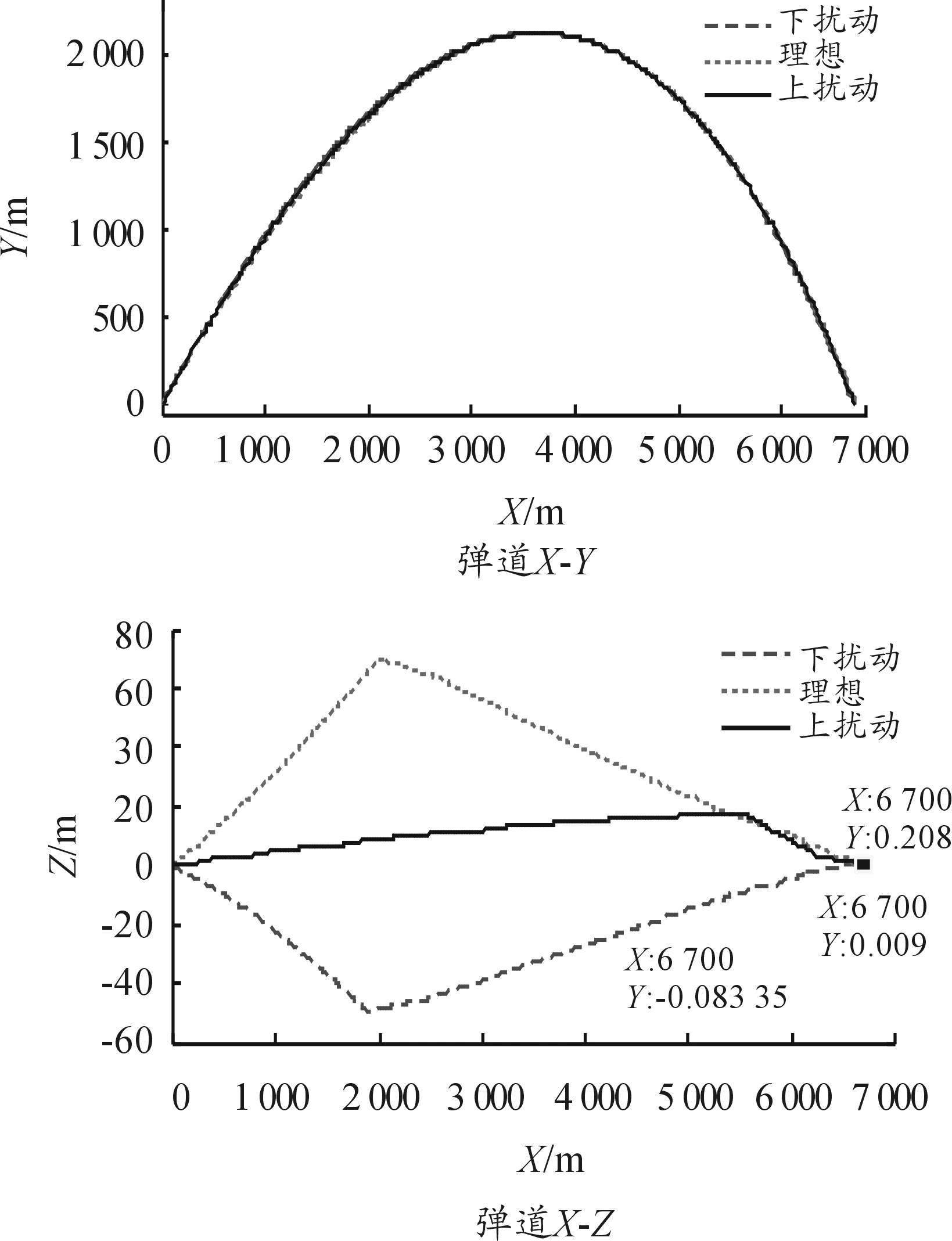
圖7 上下邊界彈道曲線

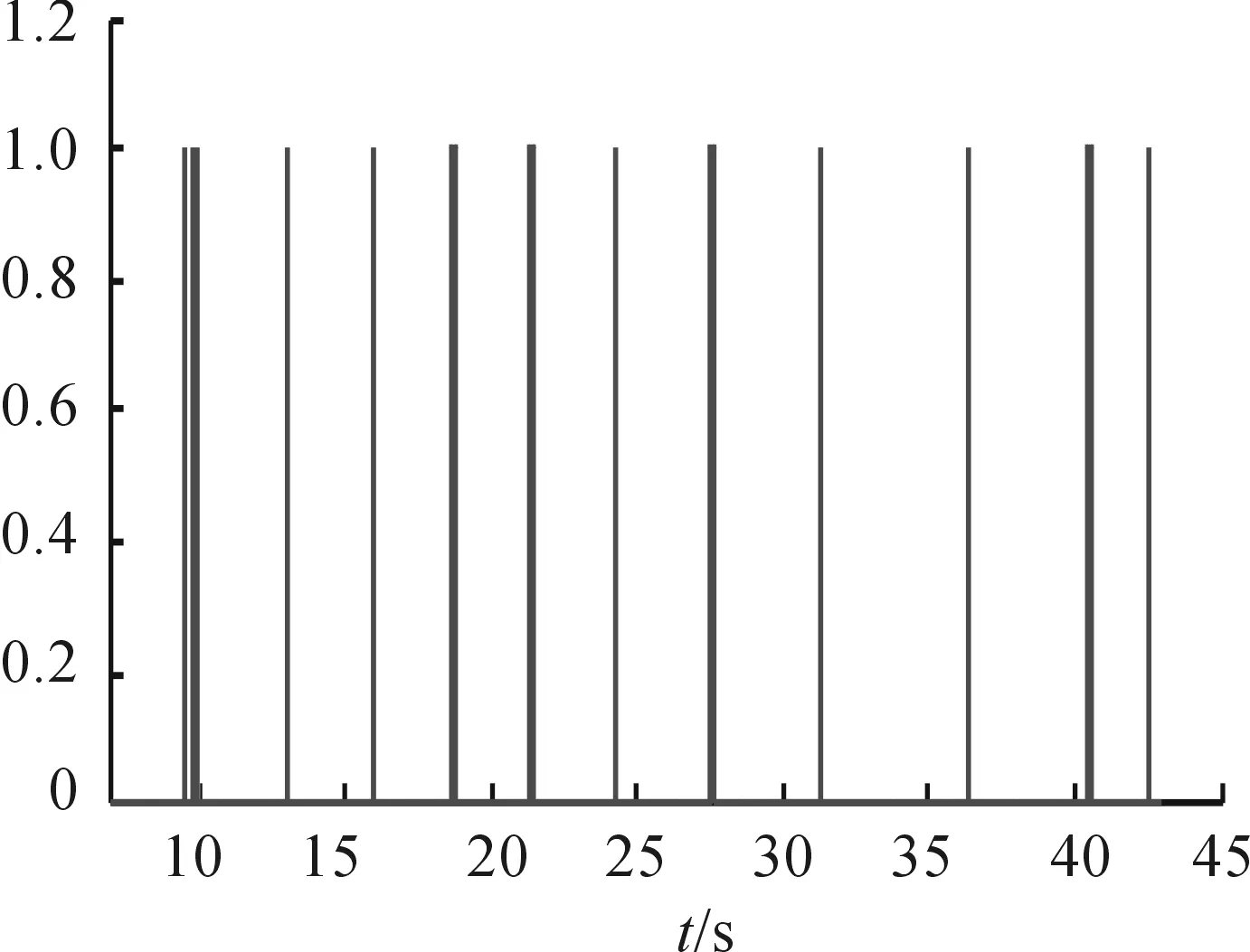
圖8 點火信號圖

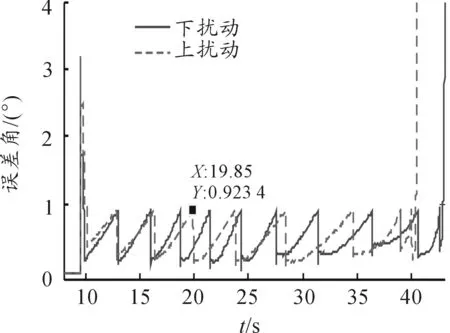
圖9 啟控后的誤差角曲線

從點火信號來看，總共點火13次，說明共點燃13個發動機。考慮一定的余量，那么該修正炮彈的發動機數量至少為16個。

從誤差角曲線上看，初始啟控時，誤差信號較大，連續啟控幾次得到修正，趨于相對穩定；在此之后，但凡誤差累積到一定量以后，就會修正一次，直至命中目標。

由此可見，脈沖修正原理可行。

3.3 修正精度仿真

由于脈沖發動機為不連續控制，理論上會存在一定的理論脫靶量，從而使得控制精度弱于氣動舵機。

基于此，可采用蒙特卡羅仿真方法，仿真分析脈沖發動機因不連續控制引起的落點散布。仿真計算時，不考慮制導誤差、姿態測量誤差、彈體誤差等，僅僅考慮不連續修正帶來的控制誤差。

仿真100條彈道，彈道散布按無控彈道散布水平進行仿真，總發動機個數取為16個。各條彈道在脈沖發動機控制下，逐漸往目標方向上收斂。仿真落點分布、各條彈道發動機工作情況見圖10。

由圖10可見，100條彈道中，平均使用發動機7.5個，最多使用14個，小于16個的總數。說明所有彈道均已收斂到目標上。

統計100條彈道的CEP為0.31 m，即因不連續控制帶來的誤差為CEP0.31 m，該值并不是一個很大的值。而對于氣動舵機，理論控制誤差在零附近，說明脈沖發動機控制精度確實差一些。

實際彈道飛行時，由于衛星定位誤差、目標指示誤差、彈體姿態測量誤差等的存在，最終的命中精度會是以上所有誤差的綜合，此時純脈沖發動機帶來的控制誤差只是一個小量。

也就是說，在最終閉環命中精度上，采用氣動舵機氣控制的命中精度并不會顯著好于采用脈沖發動機控制的精度，二者最終精度相當。

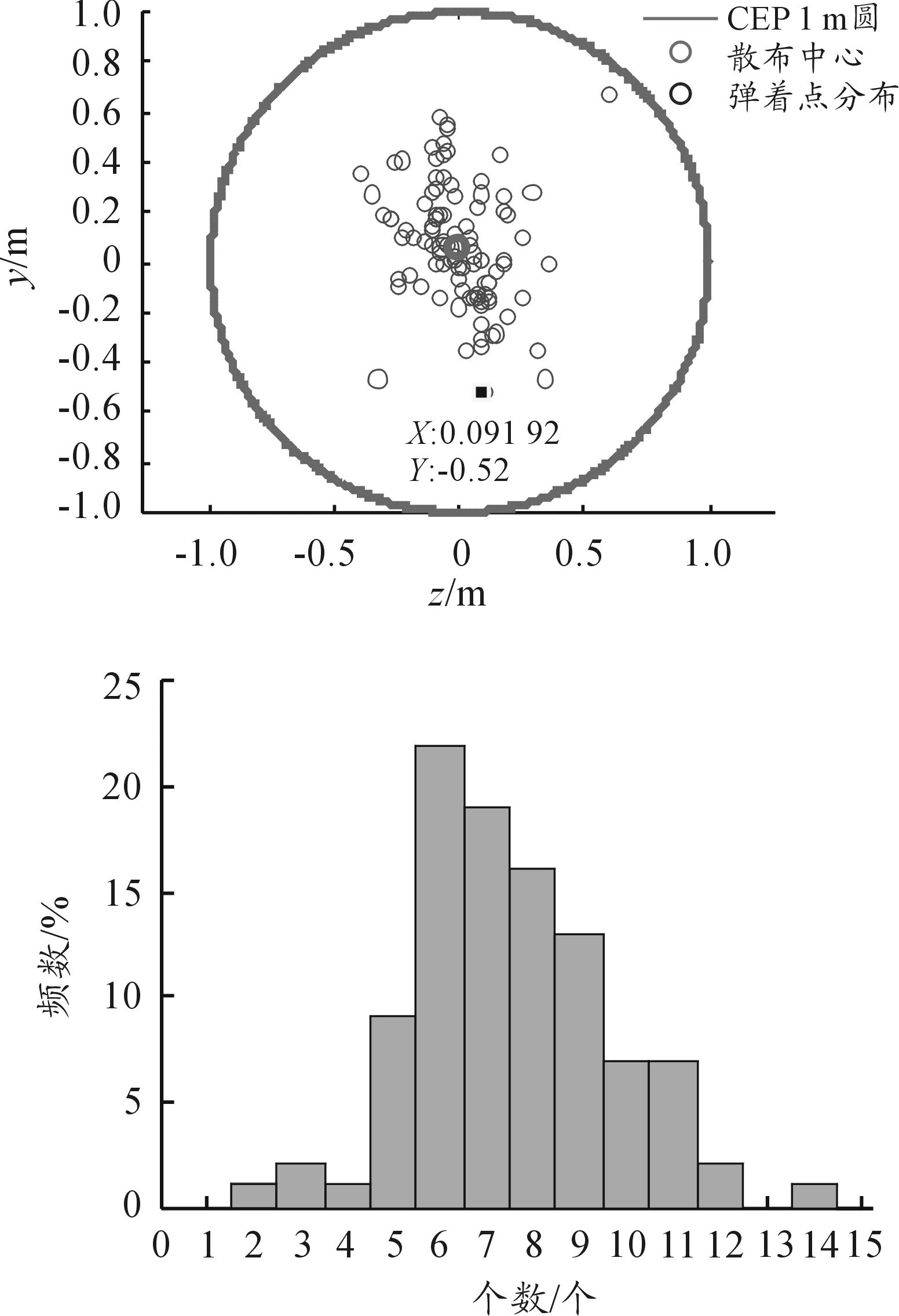
圖10 仿真結果

4 結論

本文從脈沖修正彈藥原理出發，開展了修正控制、修正策略、發動機點火策略的建模研究，并完成了初步的仿真計算分析。仿真分析表明，脈沖修正控制原理可行，彈藥命中精度與氣動舵機相當，是一種理想的低成本、高精度技術方案。

[1] 張民權，劉東方，王冬梅，等.彈道修正彈發展綜述[J].兵工學報，2010，31(2).

[2] 曹小兵.脈沖末修迫彈彈道特性分析與控制方案設計[D].南京: 南京理工大學，2012.

[3] 王強，王剛，趙瑩.國外末制導迫彈的發展綜述[J].四川兵工學報，2014，35(5).

[4] 龔鈺哲.駐阿富汗美軍裝備首批精確制導迫擊炮彈[J].外軍炮兵，2011(7).

[5] 彭博，高欣寶，張俊坤，等.衛星制導迫擊炮彈修正執行機構綜述[J]. 控制與制導, 2014(1).

[6] 楊慧娟，霍鵬飛，黃錚.彈道修正彈修正執行機構綜述[J].四川兵工學報，2011，32(1).

[7] 陳慧敏，賈平，劉華.基于半主動激光末制導的迫擊炮彈[J].光學技術，2008，34(增刊).

[8] 徐勁祥.末段修正迫彈脈沖修正方案研究[J].彈箭與制導學報, 2005, 25(1): 50 - 52.

[9] 王浩磊. 基于脈沖控制的迫彈末段彈道修正方法研究[D].南京: 南京理工大學，2012.

[10] 祁載康,曹翟,張天橋.制導彈藥技術[M ].北京:北京理工大學出版社, 2002.

ResearchonImpulseCorrectionMunitionsTechnology

CHEN Shengzheng, YANG Bo, YANG Shuanhu, DU Fenghuai, SONG Yuhang,YANG Li， GAO Xiaobo

(Xi’an Modern Control Technology Research Institute, Xi’an 710065, China)

Based on the demand of low cost precision strike of uncharged ammunition, the impulse engine was proposed as the impulse correction ammunition technology scheme. Based on the principle of impulse correction munitions, carried out the impulse correction control, correction strategy, ignition model research, and the impulse correction munitions correction principle and accuracy of the simulation analysis. The simulation analysis shows that the principle of pulsed correction ammunition is feasible, and the accuracy of the hit is not significantly weaker than that of the pneumatic steering gear, which verifies the feasibility of the principle of impulse correction ammunition.

impulse correction ammunition; impulse engine; correction of control; correction strategy

2017-08-06；

2017-09-02

陳勝政(1982—)，碩士，高級工程師，主要從事制導彈藥總體技術研究。

10.11809/scbgxb2017.12.015

本文引用格式：陳勝政，楊波，楊栓虎，等.脈沖修正彈藥技術研究[J].兵器裝備工程學報，2017(12):60-64.

formatCHEN Shengzheng, YANG Bo, YANG Shuanhu, et al.Research on Impulse Correction Munitions Technology[J].Journal of Ordnance Equipment Engineering,2017(12):60-64.

TJ41

A

2096-2304(2017)12-0060-05

(責任編輯周江川)