基于交通網絡傳遞的傳染病風險傳播模型研究?

張 玉 劉新新 蔡傳鋒 賈志娟

（鄭州師范學院 鄭州 450044）

基于交通網絡傳遞的傳染病風險傳播模型研究?

張 玉 劉新新 蔡傳鋒 賈志娟

（鄭州師范學院 鄭州 450044）

針對我國復雜交通網絡對傳染病傳播的巨大影響，提出一種基于馬可夫鏈（Markov Chain）模型構建復雜社會交通網絡中傳染病動態的傳播模型。模型以公路、高鐵、自駕及航空等人口流動常見交通網絡作為傳染病傳播模型研究的切入點，建立真實環境下的社會交通網絡拓撲結構，并構建傳染病風險指標模型。論文以近十年的新型流感病毒傳染病為例，以感染人數重癥病例數為驗證標準進行驗證。實驗結果表明，經過該模型計算傳染病傳播的結果與實際病例數據呈現正相關性，因此該模型對預測傳染病的潛在傳染風險程度具有一定的研究價值。

復雜社會交通網絡；馬爾可夫鏈；傳染病；風險指標模型

1 引言

在當今社會信息與科技發達的社會中，人與人之間無時無刻不在經過面對面接觸或是網絡等各種途徑進行頻繁的互動與交流，在這樣頻繁的人口流動下，伴隨而來的是人類的各種行為、思想和疾病的傳播與影響。尤其對于傳染病的傳播［1～2］，頻繁的人口流動更容易成為傳染病的易感人群，使得預防接種等防控措施難于落實。隨著我國各類交通運輸網的迅速發展，規模龐大的流動人口群體使得傳染病的擴散更為迅速、猛烈，為人類的生活帶來健康隱患，也給我國疫情防控帶來嚴峻挑戰。文獻［3］中指出，自1990年以來，我國國內客運量穩步增長，至2012年，全年總客運量已經超過380億人次，連續三年全年總客運量增速超過7%，其中公路系統全年發送旅客量355.7億人次，鐵路系統18.9億人次，水運系統2.6億人次，民航系統3.2億人次。交通系統的高度發達加速了傳染病的擴散。以2003年SARS疫情為例，SARS疫情于2002年11月首次在廣州佛山出現，短短數月之內迅速擴散，至5月20日，我國已有5248例確診病例。截至2003年8月7日疫情結束，此次傳染病共波及我國內地26個省、市、自治區和世界上19個國家和地區。

本文考慮到人口流動的動態因素，以各地區的人口流動產生的鏈接形態構建實際交通網絡拓撲，將馬爾可夫鏈計算模型應用到構造的網絡拓撲矩陣模型中，不僅能夠根據概率矩陣推算個體狀態的改變，而且能夠通過改變概率數組，實現能夠根據網絡狀態的隨時改變而動態改變轉移矩陣的效果，減少由于網絡狀態的隨時改變對傳染體通過網絡傳播過程的影響。同時，構建傳染病風險指標模型用于計算傳染病的危險程度。通過對本省案例的計算驗證，本模型的計算結果與本省案例結果呈正相關性，因此，本模型能夠在傳染病擴大前預先構建網絡拓撲結構模型，計算傳染病可能造成的危險程度，防患于未然。

2 基本理論介紹

2.1 傳染病與網絡結構的傳遞性

傳染病在人群中的傳播不僅取決于病原體本身，還受到人群社會網絡結構的影響。人群的復雜社會網絡結構［9～10］很大程度上決定了傳染病由一個個體傳播到另一個個體的可能性。即傳染病傳播的可能性由人群接觸網絡決定，在該接觸網絡中，每個個體表示為頂點，個體中可能導致傳染病傳播的接觸表示為個體之間的邊。這也表明了構建真實的人群接觸網絡對理解傳染病的傳播動態具有決定性的影響。因此，近年來，諸多學者加快了對城市公路、鐵路以及世界航空等接觸網絡對傳染病傳播動態影響的研究。

病原體與社會網絡結構［11］之間也存在著密不可分的關系。同一人群中，不同疾病構成的接觸網絡結構也可能存在較大差異，這主要取決于傳染病的傳播途徑。對于具有高度傳染性的疾病，其主要通過飛沫等傳播，此類疾病的接觸網絡會形成大量的邊，例如同一輛公共汽車、同一節車廂或者同一架飛機上相鄰的兩個人。而對于密切接觸傳播疾病或性傳播疾病，接觸網絡則較為稀疏。

2.2 馬爾可夫鏈模型

馬爾可夫鏈模型［12］常常被用作研究狀態轉移的預測模型，它描述了這樣一類隨機動態系統過程：系統在每個時間所處的狀態是隨機的，從一個時間的狀態按照一定的概率可以轉移到另一時間狀態，因此，從前一個狀態和轉移概率可以模擬出后一個狀態。網絡模型中狀態的轉移使用概率數組表示，利用上一次的狀態乘概率矩陣來計算和預測未來的狀態改變。模型中不同個體之間傳播的概率便組成了概率矩陣。因此，概率矩陣即表示整個復雜網絡拓撲結構。

設某系統在時刻t=n有k個可能狀態，即xn=1，2，3，…，k(n=0，1，…)，ai(n)表示系統在時刻 t=n處 于 狀 態 i的 狀 態 概 率 ，即ai(n)=P(Xn=i)，其中ai(n)=1，i=1，2，…，k 。系統在時刻n狀態為i，時刻n+1轉移到狀態 j的概率為pij(i，j=1，2，…，k)，即 pij=P(Xn+1=j|Xn=i)，稱 pij為一步轉移概率，P={pij}為一步轉移概率矩陣，簡 稱 轉 移 概 率 矩 陣 ，其 中 pij≥0，pij=1，i=1，2，…，k。k步轉移概率矩陣由一步轉移矩陣求k次冪求得。

假設系統在初始時刻t=0的狀態概率向量為a(0)=(a1(0)，a2(0)，…，ak(0))，則系統在時刻 t=1 的狀態概率向量為 a(1)=(a1(1)，a2(1)，…，ak(1))=a(0)P ，經過多次遞推過程之后，馬爾可夫預測模型為a(n)=a(0)Pn。

由馬爾可夫預測模型可知，在已知系統初始時刻t=0的狀態概率向量a(0)和狀態轉移概率矩陣P的情況下，都可以通過模型計算獲得任何時刻系統的狀態轉移概率。

3 模型設計

本文研究模型主要以河南省各地區公路、高鐵、自駕以及航空等日常交通網絡作為傳染病傳播網絡，以河南省內新型流感傳染病數據為例建立完整的傳染病指標模型，整體模型框架如圖1所示。

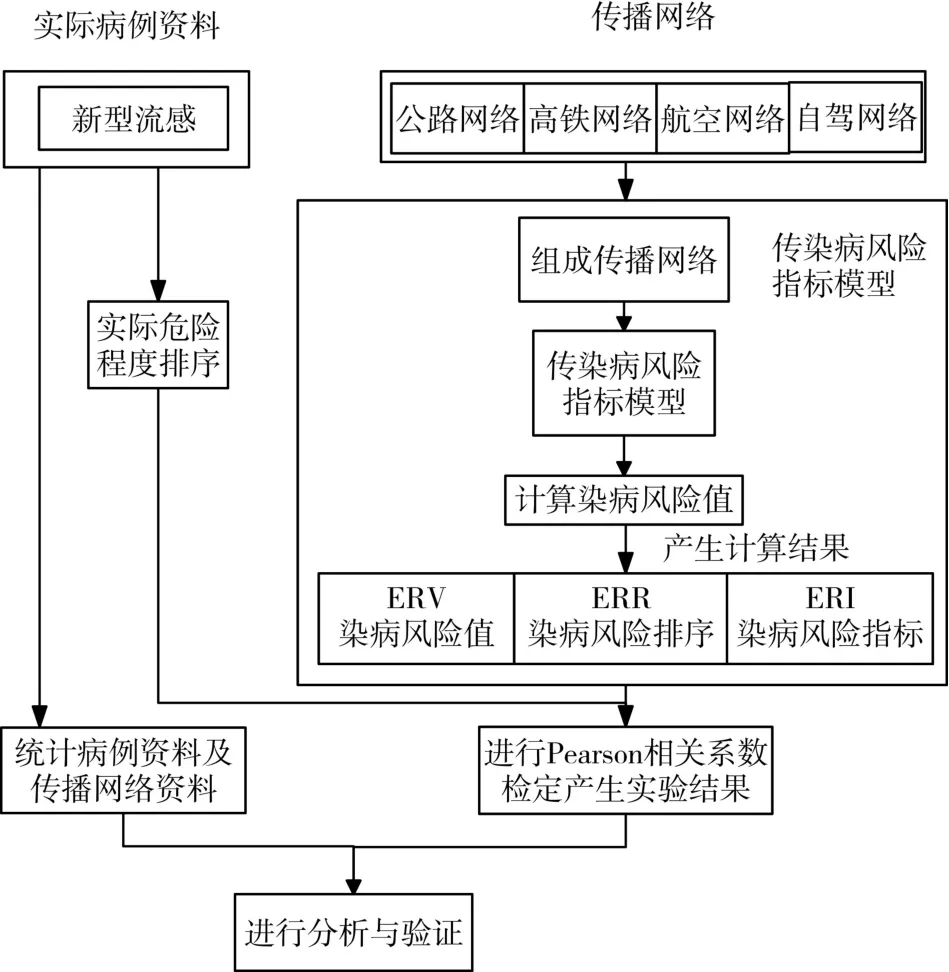
圖1 整體模型框架

3.1 人口流動交通網絡模型構建

本文選用河南省各地區的包含公路、高鐵、自駕、航空等日常人口出行方式建立人口流動交通網絡模型。主要選取河南省內管轄的18個省直市共計1892個鄉鎮構建交通網絡模型。流動人口情況由我省各交通部門匯總提供。病例數據選取近十年來新型流感病毒傳染病，由河南省衛生廳提供相關數據。

每日的交通流動人數計算公式如下：

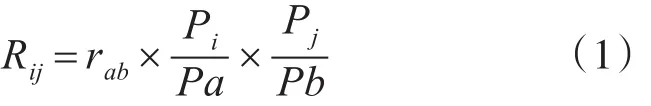
其中，Rij表示每日由i鄉鎮到鄉鎮 j的人口數，rab表示每日由地區a到地區b的人口數，Pi和Pj分別表示鄉鎮i和鄉鎮 j的人口數，Pa和Pb分別表示地區a和地區b所包含的鄉鎮總人口數。

由公路、高鐵、自駕以及航空等各個交通出行方式構成的總的交通網絡結構如下所示：

其中，W 表示整個交通網絡結構，C、R、D、A分別表示由公路、高鐵、自駕和航空出行構成的交通網絡。w1、w2、w3、w4分別表示各交通出行方式所占的比重，即通過公路、高鐵、自駕和航空出行人數占比。

3.2 流行病風險指標模型

根據在河南省建立的人口流動交通網絡狀態仿真現實社會的人口流動情況，基于馬爾可夫鏈模型構建網絡傳遞特征模型，來計算病原體隨人口流動在各地區傳播造成的流行病風險。其中，每一個個體的移動都代表著一條潛在的感染路徑。

根據病原體傳播方式，以地區A和地區B之間的人口流動傳染病傳播為例，在計算流行病風險時需要考慮以下三個問題：

1）每日從地區B流動至地區A的人口帶來的傳染風險，如圖2（b）所示。

2）白天流動到地區B受到感染后，晚上回到地區A的人口造成的傳染風險，如圖2（c）所示。

3）在本地區A范圍內進行流動造成本地區其他人口感染造成的傳染風險，如圖2（a）所示。

與此同時，通過其他方式造成傳染病的傳播風險也要考慮在本模型內。

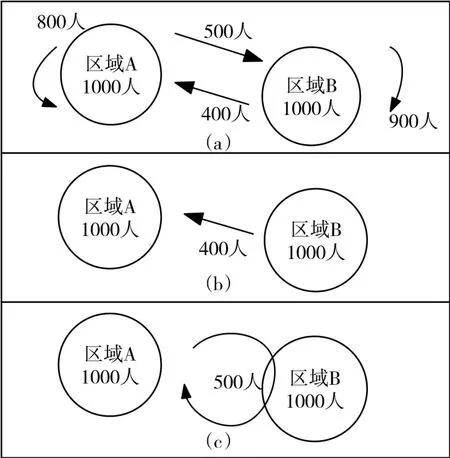
圖2 地區間人口流動感染情況

傳染病風險指標模型計算公式如下所示：

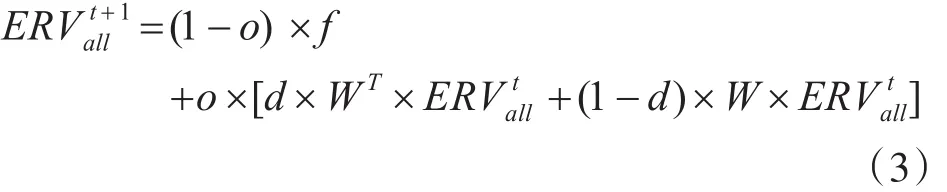
其中，公式參數描述如表1所示。

現實世界網絡傳遞過程會因某些政策的更改而隨機做出改變，而本模型中建立的人口流動交通網絡矩陣，能夠隨著迭代的過程隨時更改結構，達到了模擬真實世界的效果。

為方便各地區衛生防疫行政部門有效利用傳染數值，特定義以下三個概念，為行政處理提供相應參考。

ERV：染病風險值，計算公式停止迭代后可得到各地區的染病風險值。

ERR：染病風險排序，依據染病風險值將各地區危險程度由高到底進行排序而得，為行政決策提供依據。

ERI：染病風險指標，將各地區染病風險值除以所有地區染病風險值總和得到傳染危險程度百分比，用來比較各地區相對危險程度，為各地區加強預防與治理提供數據基礎。

表1 傳染病風險指標模型計算參數描述

3.3 流行病風險指標評估

根據本文建立的模型和實際傳染病病例數據，使用Pearson相關系數來檢定本文建立模型的準確性。具體步驟如下：

1）根據各地區的傳染病人數進行實際風險程序的計算排序，得到18個省直市地區的風險排序序列Re。

2）通過模型計算18個省直市地區風險程度進行排序，得到各地區的風險排序序列Pe。

3）使用Pearson相關系數將實際數列和計算數列進行相關程度的驗證，評估本模型計算結果的正確性。

流行病風險指標評估計算如下所示：

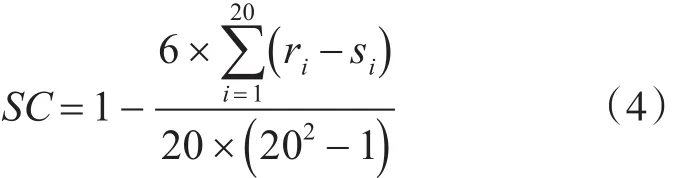
其中，Re=＜r1，r2，r3，…，r20＞ 為實際風險排序序列，Pe=＜p1，p2，p3，…，p20＞ 為模型計算風險排序序列。

4 結論驗證

通過實際分析與參考，我們發現新流感［13］的染病風險存在于各年齡階層，潛伏期一般是三天左右，而且在潛伏期也具有一定的傳染力，一般多經由接觸或飛沫傳染。因此，新流感多是通過青壯年人口交通流動造成傳染。

因此，我們假設模型中的傳染影響因素為人口交通流動進行計算。設w1=0.3，w2=0.5，w3=0.1，w4=0.1只考慮人口交通流動因素的影響，設定 o=1，設定 d∈[ ]0，1進行計算，并使用Pearson相關系數做驗證。另外，由于不同時期實際交通網絡拓撲隨時變化著，因此，我們又選取另一個時期構建交通網絡，即假設w1=0.3，w2=0.4，w3=0.1，w4=0.2，其他參數不變的情況下進行計算，同樣使用Pearson相關系數做驗證，驗證分析結果如圖3所示。當參數d=0.9時，采用第一種網絡拓撲進行計算，模型計算結果與實際病例的Pearson相關系數檢定值為0.542與采用第二種網絡拓撲進行計算的相關系數檢定值0.523大致相同，表明經過本模型的人口流動交通網絡計算各地區傳染病風險程度結果，與經由接觸及飛沫傳染的實際流行病呈現正相關性。

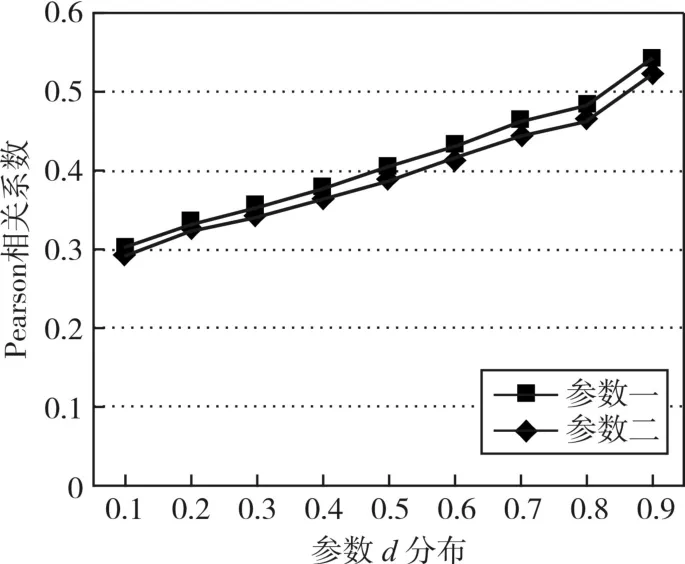
圖3 Pearson相關系數分析

5 結語

本文根據實際人口流動情況，建立包含公路、高鐵、自駕和航空在內的實際交通網絡拓撲結構，基于馬爾可夫鏈模型狀態傳遞功能計算存在于網絡拓撲中的傳遞現象，建立真實環境下的社會交通網絡拓撲結構，并構建傳染病風險指標模型。最后以河南省18個省直市共計1892個鄉鎮的新流感傳染病數據為例，以感染人數重癥病例數為驗證標準進行驗證。證明了經本模型計算傳染病傳播的結果與實際病例數據基本吻合。同時，本模型的建立能夠有效根據動態社會網絡的動態發展進行變化，對有效預測傳染病的潛在傳染風險程度提供幫助，為衛生防疫部門有效預防和控制傳染病的傳播并及時做出應急響應提供有效參考價值。下一步將考慮網絡拓撲中家庭、學校、社區等小范圍內影響因素，將構建更加細化與準確的社會網絡拓撲結構。

［1］胡明生，賈遂民，陳巧靈，等.基于常數輸入的蠕蟲傳播模型及其分析［J］.計算機工程與科學，2014，36（8）：1482-1485.HU Mingsheng，JIA Suimin，CHEN Qiaoling，et al.Analy?sis of the worm propagation model with constant immigra?tion［J］.Computer Engineering and Science，2014，36（8）：1482-1485.

［2］Hu M，Jia S，Chen Q，et al.The Analysis of Epidemic Dis?ease Propagation in Competition Environment［J］.Lecture Notes in Electrical Engineering，2013，256（1）：227-234.

［3］徐致靖.復雜社會系統中的傳染病動力學建模與案例研究［D］.北京：軍事醫學科學院，2015：13-16.XU Zhijing.Modelling the Spreading Dynamics of Infec?tious Diseases in Complex Social Systems［D］.Beijing：Academy of Military Medical Sciences，2015：13-16.

［4］Tao Li，Qiming Liu，Baochen Li.The Analysis of an SIRS Epidemic Model with Discrete Delay on Scale-Free Net?work，Applied Mathematics，2015，6（11）：1939-1946.

［5］汪小帆，李翔，陳關榮.復雜網絡理論及其應用［M］.北京：清華大學出版社，2006：345-560.WANG Xiaofan，LI Xiang，CHEN Guanrong.Complex Net?works Theory and Applications［M］.Tsinghua University Press in Beijing，2006：345-560.

［6］汪小帆，李翔，陳關榮.網絡科學導論［M］.北京：高等教育出版社，2012：121-135.WANG Xiaofan，LI Xiang，CHEN Guanrong.Network sci?ence：an introduction［M］.Higher Education Press in Bei?jing，2012：121-135.

［7］Cauchemez Simon，Bhattarai Achuyt，Marchbanks Tiffa?ny L.Role of social networks in shaping disease transmis?sion during a community outbreak of 2009 H1N1 pandem?ic influenza［J］.Proceedings of the National Academy of Sciences of the United States of America，2011，108（7）：2825-3015.

［8］Constantinos I.Siettos，Lucia Russo.Mathematical model?ing of infectious disease dynamics［J］.Virulence，2013，4（4）：295-306.

［9］Alexander Schaum，Roberto Bernal Jaquez.Estimating the state probability distribution for epidemic spreading in complex networks［J］.Applied Mathematics and Computa?tion，2016，291：197-206.

［10］胡明生，賈志娟，雷利利.基于復雜網絡的災害關聯建模 與 分 析［J］.計 算 機 應 用 研 究 ，2013，30（8）：2315-2318.HU Mingsheng，JIA Zhijuan，LEI Lili.Modeling and analysis of disasters relationship based on complex net?work［J］.Application Research of Computers，2013，30（8）：2315-2318.

［11］Yasar Tonta，Hamid R.Darvish.Diffusion of latent se?mantic analysis as a research tool：A social network anal?ysis approach［J］.Informetrics，2010，4（2）：166-174.

［12］Michela Ottobre.Markov Chain Monte Carlo and Irrevers?ibility［J］.Reports on Mathematical Physics，2016，77（3）：267-292.

［13］靳禎，孫桂全，劉茂省.網絡傳染病動力學建模與分析［M］.北京：科學出版社，2014：203-289.JIN Zhen，SUN Guiquan，LIU Maosheng.Modelling and Analysis of Epidemic Spreading on Networks［M］.Bei?jing：Science press in Beijing，2014：203-289.

Model of Transmission of Infectious Diseases Based on Traffic Network

ZHANG Yu LIU Xinxin CAI Chuanfeng JIA Zhijuan
（Zhengzhou Normal University，Zhengzhou 450044）

In view of the huge impact of the complex transportation network on the transmission of infectious diseases，a dy?namic model for the transmission of infectious diseases in complex social traffic network is proposed based on Markov Chain model.In the real environment，the social traffic network topology is established，which is based on the road，high-speed rail，car and air traffic network as the starting point of the study of the transmission model of infectious diseases，and construct the infectious disease risk index model.This paper takes the ten years of new influenza virus infectious disease as an example，the number of infections in the number of severe cases in order to verify the standard was verified.The experimental results show that the calculation model of the spread of infectious diseases results and actual case data showed positive correlation，so the potential infection risk degree of the model for predicting infectious disease has certain research value.

complex social traffic network，markov chain，infectious diseases，risk index model

Class Number TP391

TP391

10.3969/j.issn.1672-9722.2017.12.008

2017年6月2日，

2017年7月23日

國家自然科學基金項目“基于復雜網絡的傳染病溯源方法研究”（編號：U1304614）資助。

張玉，女，碩士，講師，研究方向：數據挖掘方向。劉新新，女，碩士，講師，研究方向：數據挖掘、軟件工程方向。蔡傳鋒，男，助教，研究方向：軟件工程方向。賈志娟，女，博士，教授，研究方向：人工智能、數據挖掘等。

如何構建現實世界的交通網絡模型，分析其對傳染病擴散的影響是近年來傳染病網絡傳播的一個重要研究方向。文獻［4］在無標度網絡的基礎上構造了具有社團結構的網絡模型，它將一個網絡劃分為不同的社團，以最大化提取網絡本身的主要信息，略去相對次要的信息。汪小帆［5～6］等基于節點優先提出一種新的尋找社會網絡結構中局部社團的算法，可以快速準確地尋找大規模復雜網絡的社團結構。文獻［7～8］則根據一些人口統計學數據，如年齡分布、職業分布等采用計算機生成具有某些社會網絡特征的網絡模型，但此方法構造出來的網絡一般都是靜態的并且依賴實際的研究對象，而現實中的人群結構往往是隨時間演化的，因此，無法知道網絡結構的演化對傳染病傳播的具體影響。